Smart Grid
Vol.07 No.06(2017), Article ID:22668,9
pages
10.12677/SG.2017.76049
Research about Thermal Fatigue Characteristic of IGBT Module in Considering of Electro-Thermal-Mechanism Coupling and Crack
Xiangyu Chen1, Qingyu Li1, Wenzhen Li2, Fan Yang3, Tingting He3
1State Liaoning Electric Power Co. Ltd., Panjin Power Supply Company, Panjin Liaoning
2State Grid Inner Mongolia Eastern Electric Power Co. Ltd., Hohhot Inner Mongolia
3State Key Laboratory of Power Transmission Equipment & System Security and New Technology, School of Engineering, Chongqing University, Chongqing

Received: Oct. 28th, 2017; accepted: Nov. 9th, 2017; published: Nov. 15th, 2017

ABSTRACT
Solder defect is one of the main causes of failure in power module, and the thermal stress analysis is an effective way to improve its reliability. In the paper, an electro-thermal-mechanical coupling model is built, which considers the temperature dependent of material and mechanical characteristic based on measurement parameters, and the built model is verified by experimental results. In addition, the influence of solder crack on the damage accumulation, as well as the fatigue damage under power cycling and small thermal loading cases is investigated. Finally, the condition assessment model is proposed in considering of the effect of crack damage. Results show that the built model can well characterize the influence of the solder layer void and the solder layer shedding on the thermal characteristics of the device. When the voids in the solder appear, the temperature distribution of the chip changes obviously, and the high temperature is mainly concentrated in the hollow edge region. When the fatigue layer of the solder accumulates to a certain extent, it will enter the nonlinear expansion stage. The module thermal resistance and junction temperature exponentially increase until failure.
Keywords:IGBT Module, Electro-Thermal-Mechanical Coupling, Solder Defect, Thermal Characteristics
基于电-热-力耦合模型功率器件焊料层失效下的热力特性分析
陈翔宇1,李青昱1,李文震2,杨帆3,贺婷婷3
1国网辽宁省电力有限公司盘锦供电公司,辽宁 盘锦
2国网内蒙古东部电力有限公司,内蒙古 呼和浩特
3重庆大学电气工程学院,输配电装备及系统安全与新技术国家重点实验室,重庆
收稿日期:2017年10月28日;录用日期:2017年11月9日;发布日期:2017年11月15日

摘 要
焊料层缺陷是引起功率器件失效的主要诱因之一,分析不同焊料层缺陷作用下功率器件的热力特性是提高功率器件可靠性的有效手段。本文首先建立了IGBT模块热-力特性分析的电-热-力多物理场全尺寸模型,该模型基于测量参数考虑了材料温度依赖性和力学特性;其次,分析了焊料层空洞和焊料层脱落分层在功率循环以及小载荷下对模块热力特性的影响规律。结果表明所建立的电-热-力多物理场模型能够较好表征焊料层空洞和焊料层脱落时功率器件热力特性的影响规律。当焊料层中出现空洞后,芯片表面温度分布发生了明显改变,高温主要集中在空洞边缘区域;当焊料层疲劳累积到一定程度后将进入非线性扩展阶段,模块热阻和结温呈指数函数增大,直至失效。
关键词 :IGBT模块,电-热-力耦合,焊料层缺陷,热力特性

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
变流器作为能量转换系统中最为薄弱的环节之一,超过50%的故障是由IGBT功率器件失效造成 [1] ,尽管IGBT模块失效机理极其复杂,与多种因素相关,但热载荷仍然是IGBT模块失效的最主要因素之一 [2] 。温度特性是IGBT模块产品设计和可靠性评估中的重要指标,目前已有较多学者研究IGBT模块的温度特性,主要方法包括热网络模型以及数值计算方法。基于热电比拟思想,热网络模型主要包括RC热网络以及Cauer热网络模型,但其将器件散热简化为一维问题,忽略了其热扩散 [3] 。IGBT模块由于其多层结构以及热膨胀系数不匹配,导致器件承受较大的热应力,容易发生焊料层疲劳或键合线脱落。因此,IGBT模块运行中涉及到电-热-机械应力多物理场耦合效应。然而现有关于模块温度特性的研究更多是利用简化模型或者单一场进行仿真分析,并未综合考虑模块运行中的多物理场因素相互影响 [4] [5] 。
文献 [6] 探讨了IGBT模块内部温度不均一程度与其可靠性的关系,发现温度分布严重不均一会降低器件的寿命。同时分析器件温度场和应力场分布有助于器件失效机理研究 [6] 。文献 [7] 通过研究温度循环的温度最大值和最小值对功率器件热应力的影响,揭示了温度对焊料层裂纹萌生和扩展的影响。同时实验结果指出温度幅值越大,裂纹越易萌生;而在相同波动幅值条件下,温度最大值越大,裂纹越容易萌生和扩展。文献 [8] 探讨了焊料层分层、键合线脱落、键合线规格(直径、长度、位置)对器件热响应的影响。文献 [9] 探讨了器件缺陷对温度场、热应力场的影响,发现缺陷导致芯片温度增大,空洞面积越大,热累积效应越明显,空洞附近形成的热集中点对器件的热应力场影响较大。
基于现有研究成果,为综合考虑器件内部存在的多物理场耦合效应,论文首先建立了IGBT模块的电-热-机械应力多物理场耦合模型,该模型考虑了IGBT材料的温度依赖性和力学粘塑性;其次,分析了IGBT的芯片平均温度和壳温变化规律,并实验验证了该模型的准确性;最后分析了IGBT模块在焊料层空洞、焊料层脱落分层失效形式下的温度分布规律。
2. IGBT模块的电-热-机械应力耦合场模型
2.1. 电-热-力耦合场理论计算模型
文中所研究IGBT模块简化示意图,如图1所示,模块中一般包含多个IGBT芯片和二极管芯片,其中IGBT芯片和二极管芯片并联放置在DCB铜层上。在IGBT模块中,芯片通过焊料层焊接在铜层上,而陶瓷层主要起绝缘和支撑作用,芯片通过铝键合线与铜层连接。为了获得更好的散热效果,实际运行中IGBT模块一般通过导热硅脂放置在散热器上,常见的散热器冷却方式包括水冷散热和风冷散热。
IGBT模块实际运行过程中模块各部分由于功率损耗而发热(主要发热区域为DCB陶瓷层以上部分),使得模块温度升高。而温度的改变,造成模块各部分的电气材料特性发生变化,从而造成模块的电流分布发生变化,进而影响整个器件的温度分布。因此,IGBT模块整个瞬态升温过程为一个电-热耦合动态平衡过程。
在有限元模型中,IGBT模块内部电流场方程为 [7] :
(1)
其中J和γ分别为电流密度和电导率,Qj为边界电流源。器件中导通电流将产生大量功率损耗,其为IGBT模块发热区域的内热源,从而造成器件温度升高。而单位体积的功率损耗可以根据电流场结果计算得到:
(2)
其中Qv为单位体积内的焦耳热。
IGBT模块材料参数对温度具有较强的依赖性,尤其是芯片,在其V-I输出特性线性区域中,电阻率与温度近似呈线性关系,如公式(3)所示。而铜等金属材料其电阻率可以用公式(3)表示 [8] :
(3)
其中γ20为20℃条件下的电导率,S/m;a和α均为温度系数,1/℃;T为材料温度,℃。

Figure 1. Schematic cross section of IGBT module
图1. IGBT模块简化示意图
根据传热学理论,如果考虑物体内热源影响,热传导方程为 [8] :
(4)
其中k为导热系数,W/(m∙℃);T为温度,℃;Qv为单位时间内单位体积中内热源的,W/m3;ρ为物体密度,kg/m3;c为比热容,J/(kg∙℃)。
IGBT模块温度变化过程中由于其多层结构以及不同结构之间热膨胀系数的不匹配,在受热膨胀或者变形中将受到约束,在器件内部产生热应力。因此,必须考虑IGBT模块的热-机械应力耦合效应。
根据线性热应力理论,物体的总应变由两部分相加组成:一部分是由温度变化而引起的,另一部分是由应力引起的 [9] 。
(5)
其中εth和εE分别为热应变和应力应变;E为杨氏模量,GPa;μ为泊松比;α为热膨胀系数,1/℃,T和Tref分别为温度和参考温度,℃。
2.2. IGBT模块多物理场场域参数
IGBT模块中部分材料电参数随温度而改变,必须考虑其温度特性。在模型中设定铜和硅芯片电导率随温度变化,而其他材料电导率为恒定值。根据IGBT芯片和二极管芯片的典型输出特性曲线,可知IGBT芯片电阻随着温度升高而增大,因此,其电阻率随温度变化。采用线性拟合的方法来表示电流-电压曲线线性区域中芯片的电阻率变化情况。
为了更准确表征IGBT模块材料在不同载荷下的热参数变化规律,模型中将一些材料热导率设置为与温度相关的函数。尤其是硅芯片,其导热系数随着温度增大而减小 [10] 。表1给出了模型的材料参数。
热应力计算模型中假设焊料层以外的所有材料均为弹性材料,其材料参数如表1所示。在结构力学场分析中,考虑到构成焊料层的焊锡材料熔点较低,通常室温就已经达到熔点温度一半以上,其在高温下同时具有蠕变与塑性行为,必须考虑材料粘塑性行为。文献 [11] 研究表明,Anand模型能够有效描述焊点的粘塑性特性,并可用于电子封装中焊点的可靠性模拟,因此本文采用Anand参数来描述焊料层的非弹性特性,该模型考虑到了焊料层的应变速率,温度敏感度,应变硬化和软件特性,内部损伤,结晶结构及其演化过程,其参数如表2所示。
其中s0为形变抵抗初始值;Q/R为激活能,R为气体常数,为8.314 J/(mol∙K);A为指数因子; 应力系数;m为对应于应力的应变率敏感度;n为对应于形变抵抗饱和值的应变率敏感度;a为对应于硬化应变率敏感度。
2.3. IGBT模块多物理场边界条件
当IGBT模块中通入电流时,电流通过键合线在器件内部流通,而陶瓷层由于电导率较小,在电流场中将其设置为绝缘边界。IGBT模块集电极和发射极分别注入/注出电流信号。因此,在仿真中设置集电极边界为电流终端用于表征注入电流信号,而发射极边界设置为接地。
在温度场中,由于散热器与模块物理尺寸差距较大,尤其是散热器与键合线。例如实验中散热器尺寸超过25 × 15 cm,而键合线直径小于1 mm,两者尺寸相差两个数量级。即使采用不同剖分尺寸单元,也会造成巨大的计算资源消耗,同时也可能会带来不收敛或者计算精度不够的问题。因此,在仿真中简
Table 1. Parameters of IGBT module
表1. IGBT模块材料属性
Table 2. Parameters of Anand model for solder layer
表2. 焊料层Anand材料参数
化了散热器模型,将其散热作用等效对流换热,模型中设定模块底面为对流传热边界,基板侧面也同样设置为对流换热边界,但是为自然对流。在模型中,对流换热边界可表示为 [11] :
(6)
其中h为对流换热系数,W/(m2∙℃);Tf是基板温度,℃;Tamb是环境温度,℃。由于实验对象为开封器件,仿真中考虑了开封器件中芯片表面的辐射效应,设置其为热辐射边界 [11] ,辐射率设置为0.98,与实验材料系数一致。考虑IGBT模块发热主要为向下传递,设置陶瓷层、铜终端侧面为温度场第二类边界条件,即法向热流密度值为0。IGBT模块底面设置为对流换热边界,具体数值根据对流换热定义获得,基板四周上设置为自然对流换热,其系数为12.5 W/m∙K。同时在芯片上施加根据输出特性计算得到的初始热源项,以准确表征模块发热情形。
在应力场分析中,由于实验中IGBT模块通过螺丝固定在散热器上。因此,在力学场中将其端点设置为固定位移,防止模块移动。同时基板四周设置为Z方向约束,即位移uz = 0。图2给出了有限元模型中IGBT模块的具体参数设置。
3. IGBT模块热力特性分析及验证
正常条件下IGBT模块热特性分析
散热器的冷却效果等效为对流换热,其等效系数通过实验结果测量得到。根据对流换热边界计算公式,可知:
(7)
其中Q为热量,W;h为对流换热系数,W/(m2∙℃),A为有效散热面积,m2;ΔT为底面温度与环境温度之差,℃。
实验条件下当通入电流I = 20 A,测得集电极-发射极电压Vce分别为1.359 V和1.371 V,因此热量Q分别为Vce*I = 27.2 W和27.42 W。而测得室温Ta = 24.6℃,下芯片#2的壳温Tc = 52.21℃,考虑热扩散角θ = 45˚,有效散热面积A = 31.5 mm × 67 mm。根据公式(7)可以得到对流换热系数h = 937.35 W/(m2∙℃)。而基板侧面与空气属于自然对流,其对流换热系数为h = 12.5 W/(m2∙℃)。
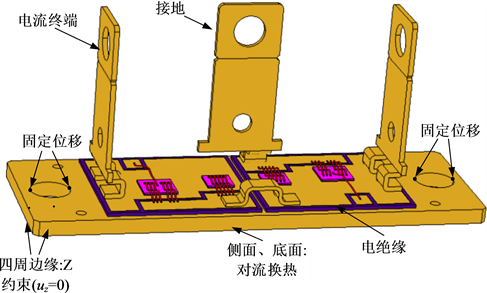
Figure 2. Boundary condition of multi-fields model
图2. 多物理场边界设置
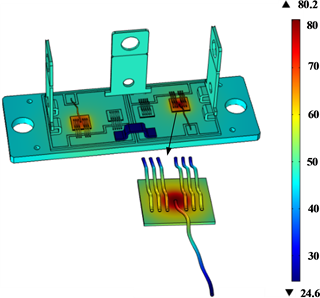
图3给出了I = 20 A条件下IGBT模块稳态温度特性,可以发现高温区域主要集中在芯片表面,尤其是与键合线接触区域。当器件达到稳态后,芯片最高温Tmax为68.72℃,而最低温为Tmin = 61.61℃。同时温度由芯片中心向边缘逐渐减小,由中心向边缘降低速率比较均匀。
图4给出了IGBT的芯片平均温度和壳温变化规律。可以发现在t = 300 s器件温度已经达到稳态,稳态值分别为66.01℃和51.9℃,并且结温上升速率明显大于壳温,主要是因为散热器热容远大于IGBT模块。
根据稳态条件下的平均结温和壳温,以及损耗计算值,即可根据热阻计算公式 得到仿真热阻值,仿真中平均损耗27.2 W,计算热阻值为0.518℃/W,而出厂数据为0.53℃/W。同样可以计算二极管热阻,仿真结果与出厂数据如表3所示。可以发现仿真结果与出厂数据之间误差较小,其中IGBT芯片计算误差为2.26%,而二极管误差为2.38%。主要原因是材料热传导系数与温度相关,而且采用等效对流换热系数代替散热器作用,也会带来一定的误差。结果仍然表明,论文模型计算结果具有较高计算精度。
4. IGBT模块不同失效形式下的温度分布研究
4.1. 焊料层空洞情形
焊料层位于模块导电、导热的主要通道上,对器件的性能和可靠性起着至关重要的作用。在制造过程中由于焊料和各种工艺因素的影响,在焊料层中很容易形成空洞。因空洞会影响热传递,造成热量堆积,温度集中,长期作用将加速焊料层损伤累积和空洞扩展,从而造成模块失效。因此论文分析了空洞对IGBT模块温度的影响规律,仿真分析中将空洞等效为圆柱体。尽管空洞位置和形状可能随机出现,但是贯穿空洞可由浅层空洞累积发展而成,并对模块损伤影响更为严重 [12] 。因此,论文以贯穿空洞为研究对象,分别研究了中心空洞和边角空洞对IGBT模块温度的影响。图5给出了相同半径不同空洞类型下的IGBT模块温度分布。
可以发现当焊料层中出现空洞后,芯片表面温度分布发生了明显改变,高温主要集中在空洞边缘区域。相同空洞半径时,中心空洞温度最大值与边角空洞温度最大值近似相同,分别为80.18℃和78.9℃。而相同半径时,边角空洞面积仅为中心空洞的1/4。因此,可以得出相同空洞面积条件下,边角空洞对中心空洞的影响更为严重,这也与现有实验结果一致 [13] 。
Table 3. Comparison of thermal impedance between datasheet and simulation results
表3. 仿真数据与出厂数据对比

Figure 3. Temperature distribution of IGBT module
图3. IGBT功率模块温度分布
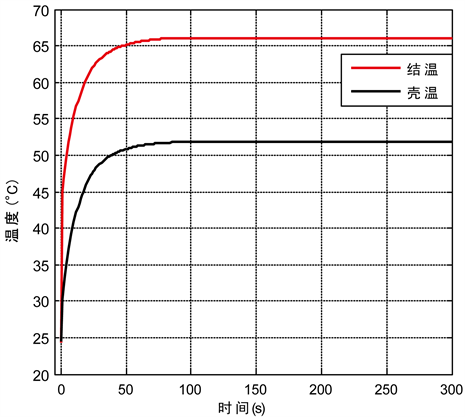
Figure 4. Variation of junction and case temperature of IGBT module
图4. IGBT模块结温和壳温变化规律
 (a) 中心空洞r = 1.5 mm
(a) 中心空洞r = 1.5 mm
 (b) 边角空洞r = 1.5 mm
(b) 边角空洞r = 1.5 mm
Figure 5. Temperature distribution for different voids
图5. 不同空洞类型下的温度分布规律
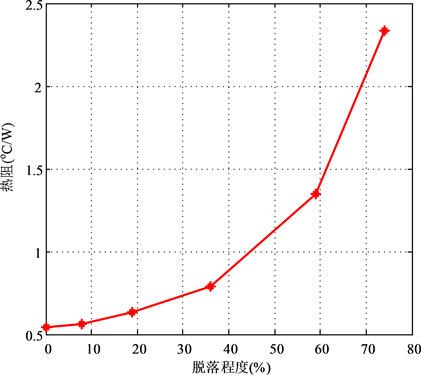
Figure 6. Simulation results for different delamination degrees
图6. 不同脱落程度下的热阻变化规律
4.2. 焊料层脱落分层情形
焊料层脱落分层是焊料层疲劳的常见模式之一,其产生的主要原因是裂纹在热应力作用下逐渐扩散,一般由焊料层边角位置向中心区域扩展。仿真中将芯片焊料层中的分层区域简化为一定厚度的“真空”域。为了进一步说明焊料层脱落程度对模块的影响,图6给出了IGBT模块不同脱落程度时的热阻变化规律。可以发现当焊料层分层面积累积到一定程度后,器件热阻迅速增大,主要原因是在该阶段中应力集中导致焊料层承受较大结温波动。当脱落分层进入扩展阶段,在温度循环作用下,焊料层脱落分层快速扩展直至失效。因此当焊料层分层萌生后或者损伤累积到一定程度后,焊料层损伤近似指数函数增大,这与现有研究结果一致:IGBT模块损伤累积过程为非线性累积过程 [13] [14] 。
5. 结论
针对焊料层缺陷引起的应力集中以及损伤反馈效应问题,论文基于IGBT模块的电-热-力多物理场模型,分析了IGBT模块在不同焊料层缺陷的下的热力特性影响规律,并实验验证了模型的准确性。最后得到了以下结论:
1) 所建立的IGBT模块的电-热-机械应力多物理场耦合模型具有较高的计算精度,能够有效反映内部缺陷对器件热力特性的影响。
2) 当焊料层中出现空洞后,芯片表面温度分布发生了明显改变,高温主要集中在空洞边缘区域。相同空洞半径时,中心空洞温度最大值与边角空洞温度最大值近似相同,分别为80.18℃和78.9℃。
3) 当焊料层疲劳累积到一定程度后将进入非线性扩展阶段,模块热阻和结温呈指数函数增大,直至失效。
文章引用
陈翔宇,李青昱,李文震,杨帆,贺婷婷. 基于电-热-力耦合模型功率器件焊料层失效下的热力特性分析
Research about Thermal Fatigue Characteristic of IGBT Module in Considering of Electro-Thermal-Mechanism Coupling and Crack[J]. 智能电网, 2017, 07(06): 443-451. http://dx.doi.org/10.12677/SG.2017.76049
参考文献 (References)
- 1. 唐勇, 汪波, 陈明, 等. 高温下的IGBT可靠性与在线评估[J]. 电工技术学报, 2014, 29(6): 17-23.
- 2. Ji, B., et al. (2015) In Situ Diagnostics and Prognostics of Solder Fatigue in IGBT Modules for Electric Vehicle Drives. IEEE Transactions on Power Electronics, 30, 1535-1543. https://doi.org/10.1109/TPEL.2014.2318991
- 3. 魏克新, 杜明星. 基于集总参数法的IGBT模块温度预测模型[J]. 电工技术学报, 2011(12): 79-84.
- 4. Košel, V., de Filippis, S., Chen, L., et al. (2013) FEM Simulation Approach to Investigate Electro-Thermal Behavior of Power Transistors in 3-D. Microelectronics Reliability, 53, 356-362. https://doi.org/10.1016/j.microrel.2012.09.002
- 5. 郑利兵, 韩立, 刘钧, 等. 基于三维热电耦合有限元模型的IGBT失效形式温度特性研究[J]. 电工技术学报, 2011(7): 242-246.
- 6. Lhommeau, T., Perpiñà, X., Martin, C., et al. (2007) Thermal Fatigue Effects on the Temperature Distribution inside IGBT Modules for Zone Engine Aeronautical Applications. Microelectronics Reliability, 47, 1779-1783.
- 7. Sauveplane, J.B., Tounsi, P., Scheid, E., et al. (2008) 3D Electro-Thermal Investigations for Reliability of Ultra Low on State Resistance Power MOSFET. Microelectronics Reliability, 48, 1464-1467.
- 8. SEMIKRON IGBT Module Datasheet, SKM50GB12T4. http://www.semikron.com
- 9. 杨世铭, 陶文铨. 传热学[M]. 北京: 高等教育出版社, 2006.
- 10. 汪泉弟, 张淮清. 电磁场[M]. 北京: 科学出版社.
- 11. Pecht, M.G. and Govind, A. (1997) In Situ Measurements of Surface Mount IC Package Deformations during Reflow Soldering. IEEE Transac-tions on Components, Packaging, and Manufacturing Technology, Part C, 20, 207-212. https://doi.org/10.1109/3476.649442
- 12. Hoad, R., Carter, N.J., Herke, D. and Watkins, S.P. (2004) Trends in EM Susceptibility of IT Equipment. IEEE Transactions on Electromagnetic Compatibility, 46, 390-395. https://doi.org/10.1109/TEMC.2004.831815
- 13. Otiaba, K.C., Okereke, M.I. and Bhatti, R.S. (2014) Numerical Assessment of the Effect of Void Morphology on Thermo-Mechanical Performance of Solder Thermal Interface Material. Applied Thermal Engineering, 64, 51-63.
- 14. Lai, W., Chen, M., Ran, L., et al. (2015) Low ΔTj Stress Cycle Effects in IGBT Power Module Die-Attach Lifetime Modelling. IEEE Transactions on Power Electronics, 39, 6575-6585.
