Management Science and Engineering
Vol.05 No.03(2016), Article ID:18488,14
pages
10.12677/MSE.2016.53013
Evolution of Cooperation Based on Evolutionary Game: A Comprehensive Review
Yaofeng Zhang
School of Statistics, Hubei University of Economics, Wuhan Hubei

Received: Aug. 15th, 2016; accepted: Sep. 1st, 2016; published: Sep. 7th, 2016
Copyright © 2016 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Evolution of cooperation is an important mechanism in social evolution process. Evolutionary game theory and computer simulation technology provide a new perspective for analyzing cooperative behavior of human. To reflect the research progress of evolution of cooperation, we reviewed literatures of cooperative evolution based on evolutionary game. Firstly, we present several evolutionary game models used in the study of evolution of cooperation. And then, main mechanisms of promoting cooperation level are summarized. Finally, important factors influences the evolution of cooperation are inducted. Based on the review of research status, further analysis on the existed problems and shortcomings is made and some perspectives on the development trends of future research are provided.
Keywords:Evolutionary Game, Evolution of Cooperation, Complex Networks, Simulation

基于演化博弈的合作进化研究综述
张耀峰
湖北经济学院统计学院,湖北 武汉

收稿日期:2016年8月15日;录用日期:2016年9月1日;发布日期:2016年9月7日

摘 要
合作的进化是人类社会演化过程中表现出的重要机制。以演化博弈为理论框架,结合计算机仿真技术分析人类合作行为,为合作进化研究提供了新的视角。为反映合作进化的研究进展,梳理了基于演化博弈的合作进化研究的相关文献。首先,给出了合作进化研究中常用的演化博弈模型,然后总结了促进合作进化的主要机制,最后归纳了影响合作进化的重要因素。在对已有研究综述的基础上,分析了已有研究的不足并进行了展望。
关键词 :演化博弈,合作进化,复杂网络,仿真

1. 引言
达尔文的生物进化理论是以生存竞争和适者生存为基础的,然而合作却普遍的存在于生物群体 [1] 。例如,吸血蝙蝠之间的喂食 [2] ,寄生在无花果中的马蜂 [3] ,等现象都是生物界中合作的真实体现。与其他生物相比,人类社会中的合作范围更加广泛。从与邻居的相处,到企业间的战略联盟,以及国家间的和平共处等等,合作在社会系统中无处不在。复杂的人类社会的形成离不开合作 [4] ,合作已经成为人类社会和生物界的一个广泛特征 [5] [6] 。
既然合作现象广泛存在,那么合作最初是如何产生的呢?对此学者展开研究并发现合作者以牺牲自身的利益来帮助其他个体,而背叛者能够在不提供回报的情况下从利他者那里获得好处。很多时候,每个个体都面临着合作与背叛的选择。合作的成本取决于合作者所接触个体的类型—合作或背叛,这是合作问题的核心 [7] 。而博弈论恰恰体现了博弈结果取决于个体选择的思想。在Von Neumann和Morgenstern 1944年出版《博弈理论和经济行为》 [8] 以及Nash在1950年提出Nash均衡(Nash equilibrium) [9] 的概念之后,博弈论(Game Theory)被广泛的应用到包括生物学、经济学、社会学、行为学、心理学等各个研究领域 [10] - [13] 。尤其当“重复囚徒困境博弈”(Iterated Prisoner’s Dilemma, IPD)被Axelord引入到合作进化理论的研究当中之后,演化博弈论(Evolutionary Game Theory) [14] 更是被广泛的作为了研究合作问题的工具 [15] 。学者们开始以演化博弈论为理论基础来研究促进合作进化的机制。一般认为有以下几种机制有利于合作的进化 [16] [17] :分别是亲缘选择(kin selection)、直接互惠(direct reciprocity)、间接互惠(indirect reciprocity)、空间或网络互惠(spatial or network reciprocity)、自愿参与(voluntary interactions)、群选择(group selection)等等。最早的亲缘选择论认为亲缘关系的远近是决定彼此合作关系的关键因素。从基因的角度来看待自然选择的观点进一步发展了亲缘选择理论,这种观点认为生物的行动受其基因的控制,目的是促进基因自身的复制。与亲缘选择论观点不同的是,Axelord认为利己者之间可以建立没有集权且不受基因遗传影响的的合作,并提出了基于“互惠利他” [18] 的互惠理论,从而开创了解释合作产生原因的新的理论框架。随后空间或网络互惠、自愿参与以及群选择理论也逐步发展。目前,如何更好地促进与巩固合作,从而维护促进社会系统稳定与人类发展,已经成为生物学、社会学、行为学、心理学等众多学科的研究热点。
2. 合作进化研究的演化博弈模型
下面,我们首先给出几种合作进化研究中的演化博弈模型。
2.1. 囚徒困境博弈
Axelord将互惠利他理论与演化博弈论相结合提出的回报理论 [19] 是以“囚徒困境”博弈(Prisoner’s Dilemma, PD)为基础的。一般形式的“囚徒困境”模型如表1所示,可简要地叙述为:博弈方1和博弈方2只有合作(Cooperation, C)或背叛(Defection, D)两种选择。双方都合作各得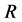 ;一方合作一方背叛时,合作方得
;一方合作一方背叛时,合作方得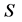 ,背叛方得
,背叛方得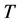 ;双方都背叛则各得
;双方都背叛则各得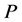 。在囚徒困境博弈模型中,所有收益满足
。在囚徒困境博弈模型中,所有收益满足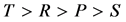 ,并且通常假设
,并且通常假设 。
。
在囚徒困境博弈模型中,尽管个体能够从相互合作中得到好处,但是由于背叛的诱惑,使得博弈双方最终都陷入了选择背叛的“困境”。囚徒困境模型属于“社会两难”(Social Dilemma) [20] 问题,是关于合作问题的最著名的隐喻。在一次或有限次囚徒困境博弈中,背叛是占优策略,即不管对方如何选择,选择背叛总是最优策略。但是当囚徒困境博弈无限次重复下去时,合作就有可能会产生,而且当贴现系数、人口结构等影响因素满足一定条件时,合作将会持续稳定下去 [1] ,这就是重复囚徒困境博弈(Iterated Prisoner’s Dilemma, IPD),也称为演化囚徒困境博弈。继Axelord之后,大多数关于合作进化的研究成果 [21] - [27] 都是建立在演化囚徒困境博弈模型的基础之上的。
演化博弈中个体可以通过上一轮的对局来决定下一轮所要采取的策略。为了验证在演化囚徒困境博弈中什么样的策略最具优势,Axelrod通过向科学家征集了根据不同策略编制的计算机程序,组织了两次程序锦标赛。其中针锋相对(Tit-for-Tat, TFT)策略在两次程序竞赛实验中都取得胜利 [1] 。该策略非常简单,其思想是博弈个体首先合作,随后重复对方上次所采用的策略。Axelrod把TFT策略的胜利归纳为以下四点:① 善良性,② 报复性,③ 宽容性,④ 清晰性。研究表明 [1] [19] [28] ,TFT策略在有效的阻止背叛的同时,对合作起到了促进并维持稳定的作用。在后期的研究中,Nowak和Sigmund [29] 的研究指出在存在“噪音”的环境中,当博弈双方都采用TFT策略时,该策略表现出了脆弱性,即对方一次小的“失误”,不论是有意的或是无意的,都将促使博弈陷入无休止的背叛之中。Boyd和Lorberbaum则认为演化囚徒困境博弈中不存在演化稳定的纯策略,TFT策略能否成功取决于群体中的环境因素 [30] 。作为TFT策略的改进,GTFT (Generous Tit For Tat)等策略被构造出来 [28] 。在所有后来的改进策略中,Pavlov (Win-stay, Lose-shift)策略最为成功 [31] 。Pavlov策略具体是指在演化囚徒困境博弈中,如果上次博弈的支付为 或
或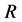 时,则博弈方继续重复以前策略,否则采用与上次博弈相反的策略 [32] 。迄今为止,Pavlov策略被认为是非常成功的一个策略 [33] ,它能够成功的打败TFT策略。Nowak等认为,Pavlov策略与TFT策略相比,能够纠正偶然的失误并且能够利用一直的合作者 [31] 。
时,则博弈方继续重复以前策略,否则采用与上次博弈相反的策略 [32] 。迄今为止,Pavlov策略被认为是非常成功的一个策略 [33] ,它能够成功的打败TFT策略。Nowak等认为,Pavlov策略与TFT策略相比,能够纠正偶然的失误并且能够利用一直的合作者 [31] 。
Doebeli和Hauert在文献 [7] 中介绍了最新的基于演化囚徒困境博弈的程序锦标赛,指出一个所谓的“串谋”策略脱颖而出。该策略只对自己的同类合作,而对其他个体采用TFT策略。为了区分同类和非同类,它们在每一轮与其他个体博弈之前都先通过一次秘密的“握手”进行身份认定。虽然该策略在身份认定机制最初如何演化等方面还有待进一步的研究,但是“串谋”的概念为心理学等学科中应用演化囚徒困境博弈研究问题提供了一个崭新的视角。
2.2. 雪堆博弈
在囚徒困境博弈中,如果合作的成本由博弈双方共同承担,并且只要有一方合作,双方收益就大于都背叛的收益时,囚徒困境博弈就可以描述为“雪堆博弈”(Snowdrift Game, SD) [34] [35] 。
SD模型可描述为:两个司机(博弈双方)被困于一个雪堆的两侧,博弈双方有铲雪(Cooperation)和不铲雪(Defection)两种选择。如果双方都铲雪,则各得R收益;如果都不铲雪,则双方的收益均为0;如果其中一方铲雪,另一方不铲,则铲雪方得S,不铲雪方得T。其中,T为顺利回家收益,铲雪会有一定的成本。则一般形式的雪堆博弈收益矩阵如表2所示。
Table 1. The payoff matrix of the prisoner’s dilemma game
表1. 囚徒困境博弈的收益矩阵
Table 2. The snowdrift game payoff matrix
表2. 雪堆博弈的收益矩阵
雪堆博弈收益矩阵中的参数满足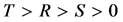 。雪堆博弈模型同样属于“社会两难”问题。但雪堆博弈模型与囚徒困境博弈模型不同之处在于,雪堆博弈模型更倾向于趋于合作。这是因为雪堆博弈模型中当对方背叛时,采取合作的行动比同样采取背叛要好。雪堆博弈模型在提出之初,就被广泛的应用到了研究生物之间的合作和冲突行为 [14] 。但是由于雪堆博弈模型不像囚徒困境博弈模型那样难以达成合作,所以作为研究合作进化的模型,被关注的较少。不过近几年来,基于雪堆博弈模型的合作问题研究已经越来越多 [36] - [40] 。这是因为雪堆博弈模型代表着人类社会另外一种情形的合作,即合作者付出代价,在利他的同时也利己。这与囚徒困境博弈模型中合作者表现出的纯粹利他有着本质的区别。所以,在雪堆博弈模型中的合作进化机制是否与囚徒困境博弈模型中的一致等问题仍然值得关注。已有研究表明 [39] 对雪堆博弈模型而言,空间结构相对均匀混合结构不利于合作的维持,这一点与囚徒困境博弈模型是不同的。
。雪堆博弈模型同样属于“社会两难”问题。但雪堆博弈模型与囚徒困境博弈模型不同之处在于,雪堆博弈模型更倾向于趋于合作。这是因为雪堆博弈模型中当对方背叛时,采取合作的行动比同样采取背叛要好。雪堆博弈模型在提出之初,就被广泛的应用到了研究生物之间的合作和冲突行为 [14] 。但是由于雪堆博弈模型不像囚徒困境博弈模型那样难以达成合作,所以作为研究合作进化的模型,被关注的较少。不过近几年来,基于雪堆博弈模型的合作问题研究已经越来越多 [36] - [40] 。这是因为雪堆博弈模型代表着人类社会另外一种情形的合作,即合作者付出代价,在利他的同时也利己。这与囚徒困境博弈模型中合作者表现出的纯粹利他有着本质的区别。所以,在雪堆博弈模型中的合作进化机制是否与囚徒困境博弈模型中的一致等问题仍然值得关注。已有研究表明 [39] 对雪堆博弈模型而言,空间结构相对均匀混合结构不利于合作的维持,这一点与囚徒困境博弈模型是不同的。
2.3. 公共品博弈
由于现实生活中往往不只是两个参与者之间的博弈,很多时候是由多个参与者进行博弈。将囚徒困境博弈推广,可以得到多人参与的公共物品博弈(Public Goods Game) [41] 。
假设有一个公共的基金,有N个参与者同时独立选择投资策略,每个参与者都有投资和不投资两个策略可选。投资者每次投资1个单位的资金,不投资者投资为0。该项目的增益系数为r (r > 1),总资金以r倍增值后平分给所有博弈参与者。显然,当r < N时,每个参与者都担心其他参与者坐享其成而选择不投资策略。因此,不投资策略是公共品博弈的纳什均衡 [42] 。该模型将囚徒困境和公共资源消耗结合起来,描述了个体理性地追求自身利益最大化的行为策略是如何导致公共利益受损的。公共品博弈说明,如果人们只关注个人利益,公共资源就得不到保护。例如,中东石油输出国组织(Organization of Petroleum Exporting Countries,简称OPEC)成立的目的之一是要限制各石油生产国的产量以保持石油价格,以便获取较高利润。但成员国并不一定遵守这个协定,而是考虑在其他成员国不增加产量的情况下自己增加一点产量对价格影响甚微,结果每个成员国都增加了产量,造成石油价格下跌。
2.4. 石头·剪刀·布博弈
石头·剪刀·布博弈源于现实生活中经常会遇到的一种用来赌胜负的简单游戏。游戏的参与双方用拳头、“剪刀手”以及手掌分别代表石头、剪刀和布,并且遵从如下的游戏规则:1) 石头赢剪刀;2) 剪刀赢布;3) 布赢石头。
如果用1代表取胜,用0代表打平,用−1代表输,则石头·剪刀·布博弈的收益矩阵可以表示为表3。
石头·剪刀·布博弈作为最古老的博弈模型之一,体现了事物间相生相克的深刻哲理,与齐威王田忌赛马博弈有相似的性质 [43] 。
3. 促进合作进化的机制
按照经典博弈论的观点,一次性或有限次的囚徒困境博弈中,个体最终都会选择背叛,而重复博弈使得合作变为可能。个体可以通过之前博弈过程的收益情况来决定下一次博弈所采取的策略,从而通过采取奖励和惩罚措施来防止对手的背叛,进而促进合作的产生与稳定。可见,对博弈模型进行适当的扩展或补充,就能够促进合作的涌现。重复博弈显然是促进合作涌现的一种机制,那么还有哪些机制能够促进产生合作以及提升合作水平的呢?近年来,越来越多的学者开始广泛关注这方面的问题 [7] [15] - [17] 。下面我们仅对促进合作进化的亲缘选择、互惠机制、群选择、自愿参与、“标签”机制、空间结构等机制进行介绍。
3.1. 亲缘选择
亲缘选择(Kin Selection) [44] 是由Hamilton在1964年提出来的,经常用来解释合作的起源。其基本思想是:生物间的亲缘关系越近,彼此就越倾向于合作,否则就越不倾向于合作。如果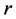 为两个体亲缘关系系数,表示两个体之间有相同基因的概率。
为两个体亲缘关系系数,表示两个体之间有相同基因的概率。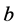 表示合作者给其他个体带来的收益,
表示合作者给其他个体带来的收益,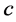 表示合作成本,那么只有当
表示合作成本,那么只有当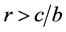 时,合作才可能产生。这个不等式又称为Hamilton规则 [44] 。亲缘选择理论经常从基因的角度解释自然选择 [45] ,认为生物进化的单元是基因,基因本质是自私的,它控制了生物的各种行为,目的是使基因本身更多、更快的复制。按照该理论,个体是否进行合作,取决于该个体与对方的亲缘关系。例如:一个父亲和他的儿子的亲缘关系系数是1/2,和他的孙子的亲缘关系系数是1/4,所以父亲的合作行为更倾向于他的儿子。
时,合作才可能产生。这个不等式又称为Hamilton规则 [44] 。亲缘选择理论经常从基因的角度解释自然选择 [45] ,认为生物进化的单元是基因,基因本质是自私的,它控制了生物的各种行为,目的是使基因本身更多、更快的复制。按照该理论,个体是否进行合作,取决于该个体与对方的亲缘关系。例如:一个父亲和他的儿子的亲缘关系系数是1/2,和他的孙子的亲缘关系系数是1/4,所以父亲的合作行为更倾向于他的儿子。
亲缘选择理论从产生之初就有着不同的理解和争论。Dawkins对“亲缘选择”是自然选择的一种特殊、复杂的形式,只有当“个体选择”不适用时才能派上用场等12个关于亲缘选择的错误理解进行了讨论 [46] 。Wilson认为,亲缘选择并不是导致利他行为的主要因素,冲突和殖民水平才是利他行为的关键因素 [47] 。Doebeli和Hauert指出 [7] 互惠利他的模型中很少考虑到亲缘选择,但是亲缘选择可以和空间囚徒困境博弈联系起来。通过个体只能与有限个邻居接触,代表亲缘选择下个体在“粘性”群体中行动,可以得到亲缘选择有利于合作提升的结论。
亲缘选择理论是合作进化的一个有力的解释机制,为研究合作问题提供了最初的框架,至今仍然是生物学界的一个研究热点。该机制不仅能部分的解释人类社会的合作现象,对动物界同类之间合作的解
Table 3. Stone scissors cloth game of gain matrix
表3. 石头·剪刀·布博弈的收益矩阵
释也很有力。但是,只靠这一种理论解释复杂的合作进化问题是远远不够的。生物界中不仅存在有亲缘关系的个体之间的合作。非亲缘关系、甚至非同类的个体间的合作现象也非常普遍 [2] [3] 那么,如何解释这些合作现象呢?Tricers的互惠利他理论 [18] 为我们提供了新的视角。
3.2. 互惠机制
互惠机制能很好地解释非亲缘关系个体以及非同类个体间的合作行为,是目前研究较多的合作进化的解释机制之一。分为直接互惠和间接互惠两类。
Tricers的互惠利他观点体现了这样一种思想,即合作可以在当前收益决定未来行动的机制下产生,上一轮两者博弈的结果作为下一轮博弈所要采取策略的参考。当然这就需要直接互惠要满足一个重要前提,即相同的两个个体要以较大的概率重复相遇。直接互惠的博弈理论模型主要是演化囚徒困境博弈。Axelrod将直接互惠机制与演化博弈论结合 [19] ,为直接互惠理论的研究开辟了道路。在
直接互惠促进合作进化的一个重要机制。能够解释相当一部分合作现象。但是其“相同的两个个体要以较大的概率重复相遇”的前提要求较高。实际中,个体的接触经常是偶然性或者频率较低的。当一个个体为其他个体提供了帮助之后,也许没有机会得到其回报。这时,间接互惠 [48] 作为合作进化的解释机制就显得尤为重要了。
Nowak和Sigmund认为由于在国际市场上一次性的交易越来越多,改变了以往企业间长期的频繁接触 [49] 。例如网上拍卖和电子商务等商业活动中大量存在一次性行为,两个体长期频繁接触的条件不能满足。这种情况下,商业个体之间是否能够合作很大程度上依靠个体的“名誉”以及建立在“名誉”基础上的相互信任。间接互惠不象直接互惠那样要求两个个体经常相遇,而是允许个体随机选择博弈对手。该机制促进合作的核心思想在于给每个个体都赋予“名誉”。Nowak形象地将直接互惠类比为“物物交换”,而把间接互惠中的“名誉”比为“货币” [16] 。拥有“货币”之后,个体就无需再与固定的对手重复接触。个体“名誉”的好坏取决于个体每次和其他对手的博弈历史,并且每个个体的“名誉”在群体中是众所周知的。拥有好的“名誉”意味着在与其他个体接触时,会得到互惠,反之将被“惩罚”。因此个体每次与对手博弈,决定采取某策略前都会考虑该策略对自己“名誉”的影响。与其他种类的生物不同,人类社会中存在大量的没有关系的个体之间的互惠现象,其中的主要原因是由于人类具有的道德情感,以及由此形成的社会规范 [50] 。因此,很多经济学家和社会学家将间接互惠和道德规范的起源联系起来 [49] 。
在最初间接互惠的研究中,个体通过积累好的名誉以在需要时得到他人的帮助。名誉的积累是靠帮助他人获得的,如果拒绝帮助他人则名誉受损。但是,这就意味着拒绝帮助欺骗者也将影响其名誉,很显然这是不公平的。Leimar和Hammerstein在该机制中加入了身份的概念 [51] 如果帮助欺骗者则该个体就拥有了坏身份,如果拒绝对欺骗者提供帮助则具有好身份。当然,对于坏身份个体帮助坏身份个体等其他情况的研究正成为另一个热点。
直接互惠和间接互惠不仅需要群体中个体间的连续接触,而且都需要个体有记忆能力,其中直接互惠只需要记忆上一轮博弈对手以及自己的策略,而间接互惠则需要记住所有个体的博弈策略历史(至少是近期策略历史)。有学者研究发现 [52] [53] 个体的记忆长度针对不同的网络结构和学习策略会带来不同的结果。正是由于间接互惠需要个体有较强的记忆能力,所以这种机制在人类社会合作进化中起到了关键作用,但是由于记忆能力的缺乏,所以该机制在动物界的作用并不明显 [16] 。不过在人类社会中,由于社会网络的复杂和广泛性,要记住群体中每个个体的策略历史,即使是在互联网等信息工具发达的今天,也是一件几乎不可能的任务。虽然间接互惠理论也具有其局限性,但是该机制仍然是解释人类社会合作进化的核心机制之一。另外信任、惩罚与奖励也是间接互惠中促进合作进化的重要影响因素 [54] [55] 。
3.3. 群选择
群选择该理论认为,自然选择是在生物种群层次上实现的,当生物个体的利他行为有利于种群利益时,这种行为就可能随种群利益的最大化而得以保存。当面临巨大灾变或是种群之间的生存竞争时,一个存在着利他主义的生物种群与一个完全缺乏这种献身精神的生物种群相比,具有更大的生存适应性。因此,利他行为可以伴随着种群的胜利而成功演化 [28] 。
本文采用Traulsen和Nowak [56] 给出的一个群选择的简单模型来说明群选择理论。该模型中,将整个人口分成一些小的群体,个体与其所在的小群体内成员进行接触,合作者帮助群体内成员,背叛者不提供帮助,个体间进行演化博弈,以此来决定他们的适应度。个体按照与他们适应度进行复制,其后代加入到与母体相同的群体。如果群体达到一定的程度则分裂成两个。同时为保证人口总数不变,会有另外一个群体消失。这样复制速度快的个体集合导致群体增大,从而分裂出更多子群体。在该模型中,只是个体进行复制,却导致了两个层次水平的选择:即低层次的群体内部的个体选择和高层次的群体之间的选择。很显然,合作者和背叛者博弈时,背叛者会获得更高适应度从而复制更快,所以在内部选择中,更倾向于背叛者;然而从群体的整体演化来看,高一层次的选择则更倾向于合作,这是因为全合作的群体比全背叛的群体复制更快。在这种机制下,为了整个种群得以顺利生存并繁衍,合作水平必然会得到提高。Traulsen和Nowak还得到了群选择条件下合作进化的基本条件: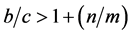 。其中
。其中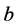 和
和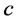 分别表示个体合作行为的收益和成本,
分别表示个体合作行为的收益和成本,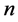 和
和 则分别表示群体最大规模和群体数量。上述模型可以推广到多于两个水平的选择以及带有移民的情况。
则分别表示群体最大规模和群体数量。上述模型可以推广到多于两个水平的选择以及带有移民的情况。
虽然群选择理论能够部分的解释生物界的合作产生的原因,但是该理论的一个致命弱点 [57] :它无法解释能够给群体带来利益,但却导致个体适应性降低的利他行为如何才能在严酷的生存竞争中对利己行为保持相对的遗传优势,从而使自己得到进化。所以,该理论在解释合作进化方面的有效性一直以来备受争议 [58] 。Foster等则认为没有亲缘选择,群选择理论很难解释利他行为 [59] 。
群选择理论中体现了个体利益和群体利益之间的矛盾。对纯粹利他有一定的解释能力,当面临种群之间的生存竞争时,一个存在着某种超越亲缘与互惠利他行为的生物种群与一个完全缺乏献身精神的生物种群相比,具有更大的生存适应性。因此,纯粹的利他行为可以伴随着种群的胜利而成功演化 [57] 。
3.4. 自愿参与
Nowak指出,在囚徒困境博弈中引入自愿参与策略也是促进合作进化的一种机制 [16] 。这里的自愿参与是指参加博弈的个体可以选择合作和背叛,还可以“单干” [60] 。选择单干策略的个体可以暂时不参与博弈,但是仍然可以得到固定的一个小收益。Szabó和Hauert在空间公共基金博弈和进化囚徒困境博弈中引入了单干策略 [61] ,对规则方格子上的研究表明,单干策略的引入可以使原先的博弈转化为了“石头–剪刀–布”类型的博弈 [62] 。吴枝喜在Szabó和Hauert的研究基础上研究了Newman-Watts (NW)小世界网络上自愿参加的空间囚徒困境博弈 [63] ,得到了一些有意义的分析结论。
3.5. 基于“标签”的机制
除了上述机制外,Riolo等人研究了一个基于“标签”的博弈模型 [64] 该模型中没有互惠机制,博弈双方根据自身某些自然特征的相似程度来决定是否进行合作,即博弈个体总是与自己的同类个体进行合作。为区别博弈对手是否为同类,可以在博弈之前进行身份确认。Roberts和Sherratt的研究指出,如果这个模型中的博弈个体可以背叛同类的话,则该博弈退化为囚徒困境博弈,那么基于标签的合作者的利益很容易被无条件的欺骗者所剥夺 [65] 。然而,Axelrod等人认为如果相互作用不是随机的,由合作者组成的集团就能够在无条件欺骗者中稳定存在,即基于标签的合作机制可以提高合作水平 [66] 。
3.6. 空间结构
最初关于合作进化机制的研究大多都是基于均匀混合群体的,即群体中每个个体都与其他所有个体存在关系连接。如果把每个个体看作是一个点,而个体间关系看作是连接点的边,那么该群体相当于一个全连通图,是全局耦合的。但是,现实中某个个体不是总能接触到群体中所有其他的个体,解决这个问题的一个方法就是引入空间结构。Axelrod的领地结构是这种思想的最初体现 [19] ,但真正把空间结构进入到合作进化研究的是Nowak和May。1992年Nowak和May突破混合均匀人口的结构框架,将进化博弈引入到空间二维格子中来 [67] [68] ,首先研究了空间二维格子上的囚徒困境博弈,即每个博弈个体跟邻近的邻居进行博弈,发现了重复囚徒困境博弈中,博弈个体的空间分布会加强合作,而Hauert等人却得到了雪堆博弈中,博弈个体的空间分布会降低合作水平的结论 [39] 。Szabo´等人利用平均场等方法,系统地研究了二维格子中的囚徒困境博弈问题 [69] 。在他们的研究中,位于二维规则格子上的个体除了和其最近邻发生博弈外,与其自身也进行博弈。对于个体的策略更新,他们首次提出了依赖于个体收益差的演化规则。考虑到生态系统中因地域环境或资源分布不均因素导致个体间具有内在非均匀性的作用。Szabo´和Hauert在空间公共基金博弈和进化囚徒困境博弈中引入了单干策略 [61] [70] ,即博弈个体不仅可以采取合作策略与欺骗策略,还可以暂时不参与博弈,但是能够得到一个小的收益。对规则方格子上的研究表明,单干策略的引入可以使原先的博弈转化为了“石头一剪刀一布”类型的博弈 [62] ,即合作策略、欺骗策略与单干策略可以通过循环入侵而得以稳定共存。Szabó等考虑策略与策略更新的复杂性,在维数为d = 1,2,3的规则格子上研究了具有外加限制条件的进化囚徒困境博弈 [71] 。个体可以采取三种策略:合作、欺骗、针锋相对,在策略更新中,博弈个体随机选择一个邻居进行比较,如果此邻居的收益比他的高,则采取此邻居的策略,否则维持自己的策略不变。
空间结构被普遍认为是促进合作进化的潜在机制之一,已经成为当今合作进化研究最多的热点领域。尤其是1998年watts的“小世界”网络 [72] 以及1999年Barabási和Albert的无标度网络 [73] 提出以来,复杂网络上的演化博弈逐渐成为研究合作进化的主要方向。2001年Abramson和Kuperman首先讨论了小世界网络上的博弈行为 [74] ,并研究了博弈行为从规则网络到小世界网络的转变。之后,结合之前讨论的互惠机制,学者们对复杂网络上的演化博弈做了大量研究 [75] [76] 。
4. 影响合作进化的因素
除了以上促进合作进化的主要机制外,还有一些影响合作水平的因素,如贴现系数、博弈顺序、博弈人数、信任、惩罚与奖励等,下面将分别介绍。
4.1. 贴现系数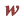
贴现系统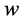 ,也称为折扣系数,它表示每一步的支付相对于上一步支付的折扣程度。
,也称为折扣系数,它表示每一步的支付相对于上一步支付的折扣程度。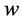 数值的大小对合作的产生有重要的影响。在一定次数的两人重复“囚徒困境”博弈中,根据逆向归纳法可知博弈双方会始终采用背叛策略。而在重复次数足够多、
数值的大小对合作的产生有重要的影响。在一定次数的两人重复“囚徒困境”博弈中,根据逆向归纳法可知博弈双方会始终采用背叛策略。而在重复次数足够多、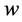 数值足够大时,合作进化才会发生。此外,
数值足够大时,合作进化才会发生。此外,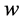 数值的大小对合作进化的演化趋势、稳定策略有重要的影响。Axelrod指出当且仅当
数值的大小对合作进化的演化趋势、稳定策略有重要的影响。Axelrod指出当且仅当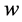 满足
满足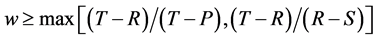 时,博弈方都采用“TFT”策略才是集体稳定策略 [1] 。还有许多的重要结论的成立条件都与
时,博弈方都采用“TFT”策略才是集体稳定策略 [1] 。还有许多的重要结论的成立条件都与 数值密切相关。
数值密切相关。
尽管合作进化的理论研究很成功,但很多学者通过实验研究指出动物在实际的“囚徒困境”中很难合作 [77] 。分析上述问题产生的原因,学者从贴现系统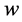 角度找到答案。实验研究表明对动物而言,学者们关于贴现系统
角度找到答案。实验研究表明对动物而言,学者们关于贴现系统 为50%的假设远远大于实际的4%,因此,动物十分偏爱眼前利益,不会采取会带来更多利益的合作策略。
为50%的假设远远大于实际的4%,因此,动物十分偏爱眼前利益,不会采取会带来更多利益的合作策略。
4.2. 博弈顺序
自从1984年,Axelrod采用计算机试验的方法,以同时决策的“囚徒困境”为研究模型进行合作进化研究以来,国内外学者大多都延续以博弈双方同时决策为假设前提对此问题进行相关研究。然而,就生物系统、社会系统中的合作问题以博弈双方同时决策为假设前提存在不合理性,轮流决策更趋于合理。在生物系统中,轮流决策导致合作的例子也已经在狒狒、吸血蝙蝠的活动中被发现。Frean [78] 及Nowak和Sigmund [32] 分别以轮流决策为博弈规则进行了相关研究。Frean研究中,“ALLD”战胜了“GTFT”策略;而一个称为“Firm but Fair”的策略(“Firm but Fair”类似“GTFT”策略,不同之处在于博弈双方都背叛时,“Firm but Fair”策略以一定比例采取合作的策略)战胜了“Pavlov”策略。Nowak和Sigmund也得出类似的结论。Hauert和Schuster进一步指出“Firm but Fair”是一个较为稳定的策略,它几乎不受记忆的长短以及背叛所得收益大小的影响 [79] 。可见,博弈顺序的不同会影响不同策略的稳定性,从而影响合作水平。
4.3. 博弈人数
大多数的合作进化研究是基于两人重复“囚徒困境”博弈(2IPD)展开的,然而,现实生活中的问题远比“2IPD”更为复杂,特别是经济系统、社会系统中的问题,如能源保护、人口增长问题等。上述的问题已无法通过“2IPD”模型来研究,因此,许多学者将“2IPD”模型拓展到“NIPD”(N > 2)模型,并对此模型进行深入研究。前边
4.4. 信任
信任问题一直是学者们,特别是社会学家们争论的焦点问题。矛盾集中体现在到底是先有合作,因此产生了信任,还是先有信任才进行合作。Axelrod主张的是一种在缺乏可预见性和信任的条件下自发产生的合作,他认为合作的基础是关系的持续性和未来影响的重要性,而非信任 [1] 。这一观点并没有受到社会学家和经济学家的认同。他们认为信任是促进合作产生的一种机制。正是由于彼此间相互信任才导致合作的产生。
目前在经济管理的研究中,信任与合作关系的研究已经成为一个热点 [83] 。这包括供应链网络、虚拟企业(动态联盟)网络、的企业集群网络等企业网络中信任与合作的问题。另外,信任经常和“名誉”、道德、情感等因素结合起来一起讨论。信任与合作的关系虽然仍在争论之中,但本文认为信任只是合作产生的充分而非必要条件。信任是合作进化的一个影响因素而非促进合作进化的机制。合作的产生不一定需要信任,但是信任能够提升网络个体间的合作水平。在企业网络中信任的引入有助于减少交易成本、促进知识共享以及增强网络应急反应能力等。
4.5. 惩罚与奖励
很显然,Axelrod主张的无集权下的自发性合作在现实生物界中大量存在,但是由于人类社会的复杂性,合作并不稳定。尤其是在各种企业网络中,合作的不稳定问题越来越多的被学者讨论 [84] 。不稳定主要来自“搭便车”等行为。因此,在进化博弈中加入惩罚和奖励(激励机制)必然能有效阻止背叛行为的蔓延,从而促进合作水平的提高。Gintis和Bowles的研究表明,较小数量的利他惩罚者可以侵入自私者人群并获得进化稳定 [85] 。其他学者也给出了不同的惩罚机制 [86] 在人类社会网络中,惩罚和奖励即为“制度”,合理制度的制定与执行必将促进合作,提高效率。
4.6. 其他因素
Santos和Pacheco等采用同步更新的策略对无标度网络上的空间纯策略博弈行为进行了研究 [87] ,发现无标度网络更有利于合作行为的产生。因此网络拓扑的异质性也是提升合作水平的一个重要因素。除了网络的异质性对合作行为有影响外,网络的平均度也是影响合作涌现的重要因素之一。TANG等研究了随机图、小世界、无标度3种网络中平均度对合作水平的影响,发现对于每种网络均存在适当的平均度使得合作水平最优 [88] 。另外,Nowak等则指出在有限人口中人口规模太大和太小都不利于合作水平的提升,个体的异质性差别也要适中才能更有效地提升合作水平 [89] 。
国内的侯云章等研究指出个体的学习行为和记忆长度都会影响群体的合作率 [53] 。偏好选择学习策略提高了无标度网络的合作水平,降低规则网络的合作水平。此时,记忆长度显著改变群体的合作水平,而个体采用随机选择策略时,记忆长度对群体的合作率产生很小的影响。另外,群体总数越高在无标度网络中合作水平越高,而小世界网络中合作水平越低,规则网络中则呈现不规则变化。进一步的研究工作又在复杂网络中引入了层次结构(hierarchical structure) [90] 、群落结构(community structure) [91] 和正负相配混合度(assortative mixing) [92] 的概念。研究发现不同网络结构对合作水平都有不同成的的影响 [75] [76] 。
5. 总结与展望
合作问题是人类社会乃至生物界的一个普遍而又复杂的问题。虽然学者们从不同的角度已经提出上述影响合作进化的各种机制和因素,但是仍然有很多的机制和因素尚未理清。主要表现在:
1) 现阶段关于合作进化的研究大多停留在仿真模型的完善与探索研究。能够把合作理论应用到实际问题的文献较少,目前只有在企业合作问题方面有所涉及;
2) 虽然已有研究对合作进化的促进机制和影响因素进行了各种讨论,但缺乏统一的理论框架,研究成果相对离散,未建立宏观理论体系;
3) 随着复杂网络的提出,学者将合作进化问题移植到抽象的复杂网络上来,但缺少利用实际人际关系网络数据进行网络建模,从而进行合作进化分析的研究。
今后的研究可以从以下几方面进行探索:
1) 在已有理论研究和建模仿真研究的基础上,积极开展结合具体领域、具体问题的应用研究,研究领域包括供应链合作、合作网络、国际政治关系、复杂社会管理等;
2) 总结归纳已有研究成果,设计基于演化博弈理论的合作进化理论框架,从整体上系统的研究合作进化问题,形成独立的理论体系;
3) 结合大数据技术,建立基于大数据的现实人际关系网络模型,从而研究现实网络上的合作进化问题,进一步深入揭示人类合作进化的内在机理和演化机制。
基金项目
湖北省自然科学基金项目(2014CFB374),湖北省教育厅科学技术研究计划重点项目(D20152202),湖北省高校优秀中青年科技创新团队计划资助项目(T201516)。
文章引用
张耀峰. 基于演化博弈的合作进化研究综述
Evolution of Cooperation Based on Evolutionary Game: A Comprehensive Review[J]. 管理科学与工程, 2016, 05(03): 113-126. http://dx.doi.org/10.12677/MSE.2016.53013
参考文献 (References)
- 1. 罗伯特•艾克斯罗德, 著.对策中的制胜之道——合作的进化[M]. 吴坚忠, 译. 上海: 上海人民出版社, 1996.
- 2. Wilkison, G.S. (1984) Reciprocal Food Sharing in the Vampire Bat. Nature, 308, 181-184. http://dx.doi.org/10.1038/308181a0
- 3. Janzen, D.H. (1979) How to Be a Fig. Annual Review of Ecology and Systematics, 10, 13-51. http://dx.doi.org/10.1146/annurev.es.10.110179.000305
- 4. Crespi, B.J. and Choe, J.C. (1997) The Evolution of Social Behavior in Insects and Arachnids. Cambridge University Press,Cambridge.
- 5. Ostrom, E., Burger, J., Field, C.B., Norgaard, R.B. and Policansky, D. (1999) Revisiting the Commons: Local Lessons, Global Challenges. Science, 284, 278-282. http://dx.doi.org/10.1126/science.284.5412.278
- 6. Fehr, E. and Fischbacher, U. (2003) The Nature of Human Altruism. Nature, 425, 785-791. http://dx.doi.org/10.1038/nature02043
- 7. Doebeli, M. and Hauert, C. (2005) Models of Cooperation Based on the Prisoner’s Dilemma and the Snowdrift Game. Ecology Letters, 8, 748-766. http://dx.doi.org/10.1111/j.1461-0248.2005.00773.x
- 8. Von Neumann, J. and Morgenstern, O. (1944) Theory of Games and Economic Behavior. Princeton University Press, Princeton.
- 9. Nash, J. (1950) The Bargaining Problem. Econometrica, 18, 155-162. http://dx.doi.org/10.2307/1907266
- 10. Hofbauer, J. and Sigmund, K. (1998) Evolutionary Games and Population Dynamics. University Press,Cambridge. http://dx.doi.org/10.1017/CBO9781139173179
- 11. Cressman, R. (2003) Evolutionary Dynamics and Extensive form Games. MIT Press, Cambridge.
- 12. Colman, A.M. (1995) Game Theory and Its Applications in the Social and Biological Sciences. Butterworth- Heinemann, Oxford.
- 13. Binmore, K.G. (1994) Playing Fair: Game Theory and the Social Contract. MIT Press, Cambridge.
- 14. Smith, J.M. and Price, G.R. (1973) The Logic of Animal Conflict. Nature, 246, 15-18. http://dx.doi.org/10.1038/246015a0
- 15. Nowak, M.A. and Sigmund, K. (2004) Evolutionary Dynamics of Biological Games. Science, 303, 793-799. http://dx.doi.org/10.1126/science.1093411
- 16. Nowak, M.A. (2006) Five Rules for the Evolution. Science, 314, 1560-1563. http://dx.doi.org/10.1126/science.1133755
- 17. Hauert, C. and Szabó, G. (2005) Game Theory and Physics. American Journal of Physics, 73, 405-414. http://dx.doi.org/10.1119/1.1848514
- 18. Trivers, R.L. (1971) The Evolution of Reciprocal Altruism. Quarterly Review of Biology, 46, 35-57. http://dx.doi.org/10.1086/406755
- 19. Axelrod, R. and Hamilton, W.D. (1981) The Evolution of Cooperation. Science, 211, 1390-1396. http://dx.doi.org/10.1126/science.7466396
- 20. Dawes, R.M. (1980) Social Dilemmas. Annual Review of Psychology, 31, 169-193. http://dx.doi.org/10.1146/annurev.ps.31.020180.001125
- 21. McNamara, J.M., Barta, Z. and Houston, A.I. (2004) Variation in Behavior Promotes Cooperation in the Prisoner’s Dilemma Game. Nature, 428, 745-748. http://dx.doi.org/10.1038/nature02432
- 22. Neill, D.B. (2001) Optimality under Noise, Higher Memory Strategies for the Alternating Prisoner’s Dilemma. Journal of Theoretical Biology, 211, 159-180. http://dx.doi.org/10.1006/jtbi.2001.2337
- 23. Killingback, T., Doebeli, M. and Knowlton, N. (1999) Variable Investment, the Continuous Prisoner’s Dilemma, and the Origin of Cooperation. Proceedings of the Royal Society of London B, 266, 1723-1728. http://dx.doi.org/10.1098/rspb.1999.0838
- 24. Masuda, N. and Aihara, K. (2003) Spatial Prisoner’s Dilemma Optimally Played in Small-World Networks. Physics Letters A, 313, 55-61. http://dx.doi.org/10.1016/S0375-9601(03)00693-5
- 25. Nowak, M.A. and Sigmund, K. (2004) Evolutionary Dynamics of Biological Games. Science, 303, 793-799. http://dx.doi.org/10.1126/science.1093411
- 26. Ishibuchi, H. and Namikawa, N. (2005) Evolution of Iterated Prisoner’s Dilemma Game Strategies in Structured Demes under Random Pairing in Game-Playing. IEEE Transactions on Evolutionary Computation, 9, 552-561. http://dx.doi.org/10.1109/TEVC.2005.856198
- 27. Scheuring, I. (2005) The Iterated Continuous Prisoner’s Dilemma Game Cannot Explain the Evolution of Interspecific Mutualism in Unstructured Populations. Journal of Theoretical Biology, 232, 99-104. http://dx.doi.org/10.1016/j.jtbi.2004.07.025
- 28. Nowak, M.A. and Sigmund, K. (1992) Tit-for-Tat in Heterogeneous Populations. Nature, 355, 250-253. http://dx.doi.org/10.1038/355250a0
- 29. Nowak, M.A. and Sigmund, K. (1990) The Evolution of Stochastic Strategies in the Prisoner’s Dilemma. Acta Applicandae Mathematicae, 20, 247-265. http://dx.doi.org/10.1007/BF00049570
- 30. Boyd, R. and Lorberbaum, J.M.D. (1987) No Pure Strategy Is Evolutionary Stable in the Iterated Prisoner’s Dilemma Game. Nature, 327, 58-59. http://dx.doi.org/10.1038/327058a0
- 31. Nowak, M.A. and Sigmund, K. (1993) A Strategy of Win-Stay, Lose Shift That Outperforms Tit-for-Tat in the Prisoner’s Dilemma Game. Nature, 364, 56-58. http://dx.doi.org/10.1038/364056a0
- 32. Nowak, M.A. and Sigmund, K. (1994) The Alternating Prisoner’s Dilemma. Journal of Theoretical Biology, 168, 219- 226. http://dx.doi.org/10.1006/jtbi.1994.1101
- 33. Kraines, D.P. and Kraines, V.Y. (2000) Natural Selection of Memory-One Strategies for the Iterated Prisoner’s Dilemma. Journal of Theoretical Biology, 203, 335-355. http://dx.doi.org/10.1006/jtbi.2000.1089
- 34. Maynard Smith, J. (1982) Evolution and the Theory of Games. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511806292
- 35. Sugden, R. (1986) The Economics of Rights, Cooperation and Welfare. Blackwell, Cornwall.
- 36. Dubois, F. and Giraldeau, L. (2003) The Forager’s Dilemma: Food Sharing and Food Defense as Risk-Sensitive Foraging Options. American Naturalist, 162, 768-779. http://dx.doi.org/10.1086/379202
- 37. Posch, M., Pichler, A. and Sigmund, K. (1999) The Efficiency of Adapting Aspiration Levels. Proceedings of the Royal Society of London B, 266, 1427-1435. http://dx.doi.org/10.1098/rspb.1999.0797
- 38. McElreath, R. (2003) Reputation and the Evolution of Conflict. Journal of Theoretical Biology, 220, 345-357. http://dx.doi.org/10.1006/jtbi.2003.3166
- 39. Hauert, C. and Doebeli, M. (2004) Spatial Structure Often Inhibits the Evolution of Cooperation in the Snowdrift Game. Nature, 428, 643-646. http://dx.doi.org/10.1038/nature02360
- 40. Shang, L.H., Li, X. and Wang, X.F. (2006) Cooperative Dynamics of Snowdrift Game on Spatial Distance-Dependent Small-World Networks. European Physical Journal B, 54, 369-373. http://dx.doi.org/10.1140/epjb/e2006-00454-8
- 41. Hardin, G. (1968) The trAgedy of the Commons. Science, 162, 1243-1248. http://dx.doi.org/10.1126/science.162.3859.1243
- 42. Hauert, C., Monte, S.D., Hofbauer, J. and Sigmund, K. (2002) Replicator Dynamics for Optional Public Good Games. Journal of Theoretical Biology, 218, 187-194. http://dx.doi.org/10.1006/jtbi.2002.3067
- 43. 谢识予. 经济博弈论[M]. 第二版. 上海: 复旦大学出版社, 2002.
- 44. Hamilton, W.D. (1964) The Genetical Evolution of Social Behavior. I. Journal of Theoretical Biology, 7, 1-16. http://dx.doi.org/10.1016/0022-5193(64)90038-4
- 45. Dawkins, R. (1976) The Selfish Gene. Oxford University Press, Oxford.
- 46. Dawkins, R. (1979) Twelve Misunderstandings of Kin Selection. Zeitschrift für Tierpsychologie, 51, 184-200.
- 47. Wilson, E.O. (2005) Kin Selection as the Key to Altruism: Its Rise and Fall. Social Research, 72, 159-168.
- 48. Nowak, M.A. and Sigmund, K. (1998) Evolution of Indirect Reciprocity by Image Scoring. Nature, 393, 573-577. http://dx.doi.org/10.1038/31225
- 49. Nowak, M.A. and Sigmund, K. (2005) Evolution of Indirect Reciprocity. Nature, 437, 1291-1298. http://dx.doi.org/10.1038/nature04131
- 50. Henrich, J., Boyd, R., Bowles, S., Camerer, C., Fehr, E. and Gintis, H. (2001) Cooperation, Reciprocity and Punishment in Fifteen Small-Scale Societies. American Economic Review, 91, 73-78. http://dx.doi.org/10.1257/aer.91.2.73
- 51. Leimar, O. and Hammerstein, P. (2001) Evolution of Cooperation through Indirect Reciprocity. Proceedings of the Royal Society of London B, 268, 745-753. http://dx.doi.org/10.1098/rspb.2000.1573
- 52. Milinski, M., Semmann, D., Bakker, T.C.M. and Krambeck, H.J. (2001) Cooperation through Indirect Reciprocity: Image Scoring or Standing Strategy? Proceedings of the Royal Society of London B, 268, 2495-2501. http://dx.doi.org/10.1098/rspb.2001.1809
- 53. 侯云章, 盛昭瀚, 王晓灵, 陈国华. 复杂网络中基于记忆长度的合作行为[J]. 系统工程理论与实践, 2008, 28(2): 119-124.
- 54. Sigmund, K., Hauert, C. and Nowak, M.A. (2001) Reward and Punishment. Proceedings of the National Academy of Sciences of the United States of America, 98, 10757-10762. http://dx.doi.org/10.1073/pnas.161155698
- 55. Brandt, H., Hauert, C. and Sigmund, K. (2003) Cooperation, Punishment and Reputation in Spatial Games. Proceedings of the Royal Society of London B, 270, 1099-1104. http://dx.doi.org/10.1098/rspb.2003.2336
- 56. Traulsen, A. and Nowak, M.A. (2006) Evolution of Cooperation by Multilevel Selection. Proceedings of the National Academy of Sciences of the United States of America, 103, 10952-10955. http://dx.doi.org/10.1073/pnas.0602530103
- 57. 张四海. 基于社会网络和博弈论的合作理论研究[D]: [博士学位论文]. 合肥: 中国科技大学, 2006.
- 58. Thompson, N.S. (2000) Shifting the Natural Selection Metaphor to the Group Level. Behavior and Philosophy, 28, 83-101.
- 59. Foster, K.R., Wenseleers, T. and Ratnieks, F.L.W. (2006) Kin Selection Is the Key to Altruism. Trends in Ecology and Evolution, 21, 57-60. http://dx.doi.org/10.1016/j.tree.2005.11.020
- 60. Hauert, C., De Monte, S., Hofbauer, J. and Sigmund, K. (2002) Volunteering as Red Queen Mechanism for Cooperation in Public Goods Games. Science, 296, 1129-1132. http://dx.doi.org/10.1126/science.1070582
- 61. Szabó, G. and Hauert, C. (2002) Evolutionary Prisoner’s Dilemma Games with Voluntary Participation. Physical Review E, 66, Article ID: 062903. http://dx.doi.org/10.1103/physreve.66.062903
- 62. Semmann, D., Krambeck, H.J. and Milinski, M. (2003) Volunteering Leads to Rock-Paper-Scissors Dynamics in a Public Goods Game. Nature, 425, 390-393. http://dx.doi.org/10.1038/nature01986
- 63. 吴枝喜. 复杂网络及其上的进化博弈研究[D]: [博士学位论文]. 兰州: 兰州大学, 2007.
- 64. Riolo, R.L., Cohen, M.D. and Axelrod, R. (2001) Evolution of Cooperation without Reciprocity. Nature, 414, 441-443. http://dx.doi.org/10.1038/35106555
- 65. Roberts, G. and Sherratt, T.N. (2002) Does Similarity Breed Cooperation? Nature, 418, 499-500. http://dx.doi.org/10.1038/418499b
- 66. Axelrod, R., Hammond, R.A. and Grafen, A. (2004) Altruism via Kin-Selection Strategies That Rely on Arbitrary Tags with Which They Coevolve. Evolution, 58, 1833-1838. http://dx.doi.org/10.1111/j.0014-3820.2004.tb00465.x
- 67. Nowak, M.A. and May, R.M. (1992) Evolutionary Games and Spatial Chaos. Nature, 359, 826-829. http://dx.doi.org/10.1038/359826a0
- 68. Nowak, M.A. and May, R.M. (1993) The Spatial Dilemmas of Evolution. International Journal of Bifurcation and Chaos, 3, 35-78. http://dx.doi.org/10.1142/S0218127493000040
- 69. Szabó, G. and Töke, C. (1998) Evolutionary Prisoner’s Dilemma Game on a Square Lattice. Physical Review E, 58, 69-73. http://dx.doi.org/10.1103/PhysRevE.58.69
- 70. Szabó, G. and Töke, C. (2002) Phase Transitions and Volunteering in Spatial Public Goods Games. Physical Review Letters, 89, Article ID: 118101. http://dx.doi.org/10.1103/physrevlett.89.118101
- 71. Szabó, G., Antal, T., Szabo, P. and Droz, M. (2000) Spatial Evolutionary Prisoner’s Dilemma Game with Three Strategies and External Constraints. Physical Review E, 62, 1095-1103. http://dx.doi.org/10.1103/PhysRevE.62.1095
- 72. Watts, D.J. and Strogatz, S.H. (1998) Collective Dynamics of “Small-World” Networks. Nature, 393, 440-442.. http://dx.doi.org/10.1038/30918
- 73. Barabási, A.L. and Albert, R. (1999) Emergence of Scaling in Random Networks. Science, 286, 509-512. http://dx.doi.org/10.1126/science.286.5439.509
- 74. Abramson, G. and Kuperman, M. (2001) Social Games in a Social Network. Physical Review E, 63, Article ID: 030901. http://dx.doi.org/10.1103/physreve.63.030901
- 75. 王龙, 伏锋, 陈小杰, 王靖, 李卓政, 谢广明, 楚天广. 复杂网络上的演化博弈[J]. 智能系统学报, 2007, 2(2): 1-10.
- 76. 赵晟莹, 郭强, 王文旭, 任杰, 刘建国. 复杂网络上博弈行为的研究进展[J]. 电子测量技术. 2007, 30(4): 93-96.
- 77. Stephens, D.W., Mclinn, C.M. and Stevens, J.R. (2002) Discounting and Reciprocity in an Iterated Prisoner’s Dilemma. Science, 298, 2216-2218. http://dx.doi.org/10.1126/science.1078498
- 78. Frean, M.R. (1994) The Prisoner’s Dilemma without Synchrony. Proceedings of the Royal Society B, 257, 75-79. http://dx.doi.org/10.1098/rspb.1994.0096
- 79. Hauert, C.H. and Schuster, H.G. (1998) Extending the Iterated Prisoner’s Dilemma without Synchrony. Journal of Theoretical Biology, 192, 155-166. http://dx.doi.org/10.1006/jtbi.1997.0590
- 80. Mataushima, M. and Ikegami, T. (1998) Evolution of Strategies in the Three-Person Iterate Prisoner’s Dilemma. Journal of Theoretical Biology, 195, 53-67. http://dx.doi.org/10.1006/jtbi.1998.0780
- 81. Yao, X. and Darwen, P. (1994) An Experimental Study of N-Person Iterated Prisoner’s Dilemma Games. Informatica, 18, 435-450.
- 82. Seo, Y.G. and Cho, S.B. (1999) An Evolutionary Study on Cooperation in N-Person Iterated Prisoner’s Dilemma Game. 2nd Asia-Pacific Conference on Simulated Evolution and Learning, Canberra, 24-27 November 1998, 301-308. http://dx.doi.org/10.1007/3-540-48873-1_39
- 83. Morgan, R.M. and Hunt, S.D. (1997) The Commitment-Trust Theory of Relationship Marketing. Journal of Marketing, 58, 20-38. http://dx.doi.org/10.2307/1252308
- 84. Spekman, R.E., Isabella, L.A. and Macavor, T.C. (1998) Alliances Management: A View from Past and a Look to the Future. Journal of Management Studies, 35, 747-772. http://dx.doi.org/10.1111/1467-6486.00118
- 85. Giniis, H. and Bowles, S. (2004) The Evolution of Strong Reciprocity: Cooperation in Heterogeneous Populations. Theoretical Population Biology, 65, 17-28. http://dx.doi.org/10.1016/j.tpb.2003.07.001
- 86. Henrieh, J. and Boyd, R. (2001) Why People Punish Defectors: Weak Conformist Transmission Can Stabilize Costly Enforcement of Norms in Cooperative Dilemmas. Journal of Theoretical Biology, 208, 79-89. http://dx.doi.org/10.1006/jtbi.2000.2202
- 87. Santos, F.C. and Pacheco, J.M. (2005) Scale-Free Networks Provide a Unifying Framework for the Emergence of Cooperation. Physical Review Letters, 95, Article ID: 098104. http://dx.doi.org/10.1103/physrevlett.95.098104
- 88. Tang, C.L., Wang, W.X., Wu, X. and Wang, B.H. (2006) Effect of Average Degree on Cooperation in Networked Evolutionary Game. European Physical Journal B, 53, 411-415. http://dx.doi.org/10.1140/epjb/e2006-00395-2
- 89. Nowak, M.A., Sasaki, A., Taylor, C. and Fuden-Berg, D. (2004) Emergence of Cooperation and Evolutionary Stability in Finite Populations. Nature, 428, 646-650. http://dx.doi.org/10.1038/nature02414
- 90. Scott, J. (2000) Social Network Analysis. 2nd Edition, Sage, London.
- 91. Newman, M.E.J. (2002) Assortative Mixing in Networks. Physical Review Letters, 89, Article ID: 208701. http://dx.doi.org/10.1103/physrevlett.89.208701
- 92. Newman, M.E.J. (2006) The Structure and Function of Complex Networks. SIAM Review, 45, 167-256. http://dx.doi.org/10.1137/S003614450342480
