Advances in Applied Mathematics
Vol.3 No.02(2014), Article
ID:13470,4
pages
DOI:10.12677/AAM.2014.32008
曲面上色临界图点数的上界
Qingqing Li, Fugang Chao, Weihua Lu, Han RenDepartment of Mathematics, East China Normal University, Shanghai
Email: chaofugang@126.com, hren@math.ecnu.edu.cn
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Mar. 18th, 2014; revised: Apr. 16th, 2014; accepted: Apr. 22nd, 2014
ABSTRACT
Dirac observed that, for each fixed surface and each natural number k ≥ 8, there are only finitely many k-color-critical graphs on S. Mohar and Thomassen proved that for a surface S of genus g ≥ 2, every 7-color-critical graph on S has less than 138(g ‒ 1) vertices. Using Euler formula and the critical-graphs methods of Gallai, we improve this result and give a simple proof that the number of 7-color-critical graphs is finite. We also give unified expression for an upper bound of vertices of k-color-critical graphs (k ≥ 7) on surfaces.
Keywords:Embedding, Genus, Coloring, Color-Critical Graph

曲面上色临界图点数的上界
李青青,晁福刚,路伟华,任 韩
华东师范大学数学系,上海
Email: chaofugang@126.com, hren@math.ecnu.edu.cn
收稿日期:2014年3月18日;修回日期:2014年4月16日;录用日期:2014年4月22日

摘 要
Dirac观察到:对每个固定的曲面S和每个固定的自然数k ≥ 8,曲面S上仅有有限多个k-色临界图。Mohar和Thomassen证明了:对于亏格g ≥ 2的曲面S,曲面S上的7-色临界图的点数少于138(g ‒ 1)。我们借助于Euler公式和Gallai所发展起来的研究色临界图的方法,改进了这个结果,给出了曲面S上的7-色临界图的个数是有限的一个比较简洁的证明。除此以外,我们还给出曲面S上的每一个k-色临界图(k ≥ 7)的点数上界的一个统一的表达式。
关键词
嵌入,亏格,着色,色临界图

1. 引言
图G是由有限的点集V(G) 和称之为边的无序的点对的集合E(G)构成。如果边xy表现,我们称x和y相邻或者相连,x和y是邻点。点x的度是指其邻点的数目,记作d(x)。如果所有的点的度数都是r,那么G是r-正则的。如果H是G的一个子图,称G(H)是H的诱导子图,它是由H及G中连接H的两个点的所有边组成。我们定义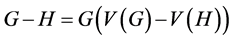 。如果v是图G中的一个点,那么或N(v)是G的由v的邻点诱导的子图。
。如果v是图G中的一个点,那么或N(v)是G的由v的邻点诱导的子图。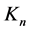 是n个点的完全图;也就是说,
是n个点的完全图;也就是说,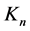 的所有点的度数都是
的所有点的度数都是![]() 。
。
曲面S是一个没有边界的、紧的、连通的2-维流形。曲面分类定理告诉我们:每个曲面或者同胚于 ,添加了g个手柄的球,或者同胚于
,添加了g个手柄的球,或者同胚于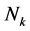 ,添加了k个叉帽的球。这个定理是由Möbius[1] 和Jordan[2] 最早提出的。Thomassen[3] 给出了它的一个简单而又严格的证明。令
,添加了k个叉帽的球。这个定理是由Möbius[1] 和Jordan[2] 最早提出的。Thomassen[3] 给出了它的一个简单而又严格的证明。令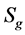 和
和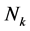 表示亏格为g(或叉帽数为k)的可定向(或不可定向)曲面。一个图G的亏格g(G)(或不可定向亏格(G),也称叉帽数)是最小的整数g(或k),使得G,可以嵌入到
表示亏格为g(或叉帽数为k)的可定向(或不可定向)曲面。一个图G的亏格g(G)(或不可定向亏格(G),也称叉帽数)是最小的整数g(或k),使得G,可以嵌入到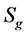 (或
(或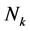 )上,且边为两两不交的简单闭曲线。G在
)上,且边为两两不交的简单闭曲线。G在![]() 上的嵌入总是2-胞腔嵌入(见[3] )。当
上的嵌入总是2-胞腔嵌入(见[3] )。当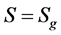 时,曲面S的Euler亏格为γ=2g,当
时,曲面S的Euler亏格为γ=2g,当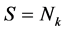 时,曲面S的Euler亏格为γ = k。特别地,
时,曲面S的Euler亏格为γ = k。特别地,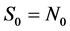 是球,
是球, 是环面,
是环面, 是射影平面,
是射影平面,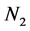 是Klein瓶。
是Klein瓶。
记n,e,f分别为图G的边数、点数和面数。经典的Euler公式[4] 告诉我们: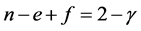 ,其中γ为图G的Euler亏格。更一般地,我们可以分成可定向和不可定向曲面来考虑。设一个连通图G是曲面S上的一个2-胞腔嵌入,其中
,其中γ为图G的Euler亏格。更一般地,我们可以分成可定向和不可定向曲面来考虑。设一个连通图G是曲面S上的一个2-胞腔嵌入,其中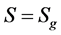 或
或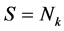 。称一个面的边界为一条面迹。分别记面的数目为f,
。称一个面的边界为一条面迹。分别记面的数目为f,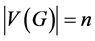 和
和 ,Euler公式可以写成如下形式:
,Euler公式可以写成如下形式: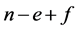 等于
等于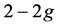 (当
(当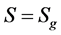 )或
)或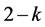 (当
(当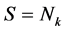 )。
)。
图G的一个嵌入是一个有序对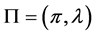 ,其中
,其中 是一个旋转系统(这意味着,对每个点v,
是一个旋转系统(这意味着,对每个点v,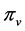 是与v关联的边的一个轮换),λ是分配给每条边
是与v关联的边的一个轮换),λ是分配给每条边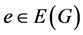 一个符号
一个符号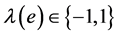 的一个符号映射。给定G的一个嵌入П,我们说G是П-嵌入的。Edmonds[5] 和Heffter[6] 的结果表明:图G在某个曲面S上一个嵌入是由它的旋转系统确定。
的一个符号映射。给定G的一个嵌入П,我们说G是П-嵌入的。Edmonds[5] 和Heffter[6] 的结果表明:图G在某个曲面S上一个嵌入是由它的旋转系统确定。
图G的一个k-着色是一个映射 ,(称
,(称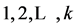 为颜色),使得任意两个相邻的顶点都分配到不同的颜色。称图G是可k-着色的,如果G有一个k-着色。图G的色数,记作𝜒(G),是最小的数k,使得G有一个k-着色,但没有
为颜色),使得任意两个相邻的顶点都分配到不同的颜色。称图G是可k-着色的,如果G有一个k-着色。图G的色数,记作𝜒(G),是最小的数k,使得G有一个k-着色,但没有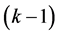 -着色。曲面嵌入图的色数,是指嵌入到某个曲面上的图的最大色数。在研究曲面嵌入图的着色问题时,色临界图起着重要的作用。称一个图G为k-色临界的,如果G不是
-着色。曲面嵌入图的色数,是指嵌入到某个曲面上的图的最大色数。在研究曲面嵌入图的着色问题时,色临界图起着重要的作用。称一个图G为k-色临界的,如果G不是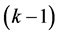 -色的,但它的每个真子图都是
-色的,但它的每个真子图都是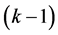 -色的。
-色的。
当研究曲面嵌入图的着色问题时,因为许多的信息隐藏在了亏格的后面,所以问题就变得有些扑朔迷离。在平面图的四色猜想还未解决的时候,数学家为了研究这个猜想,对曲面嵌入图的色数进行
了探究。Heawood[7] 证明了:如果S不是球,那么嵌入到S上的每个图至多使用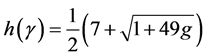
种不同的颜色,其中g为S的亏格。Ringel和Youngs[8] 证明了这个结果对除了Klein瓶以外的所有曲面都是最好可能的。嵌入到Klein瓶上的图仅需6种颜色,而Heawood的界告诉我们Klein瓶上的嵌入图的最大色数为7,这个结果是由Franklin[9] 得到的。Dirac[10] ,Albertson和Hutchinson[11] 证明了:曲面S上的一个图可以用少于h(γ)种颜色着色,除非它包含一个h(γ)个点的完全图作为子图。
研究曲面上的色临界图,既要探讨它的组合特征,又要考虑它在曲面上的嵌入行为,所以有一定的难度。1997年,Gimbel和Thomassen[12] 提出了曲面色临界图猜想:令S是任意一个固定的曲面,令k,q是两个>2的固定的自然数,曲面S上是否存在无限多围长为q的k-色临界图。这是一个富有创造力的设想。Erdös关于大围长同时有大色数的存在性结果为这个想法提供了基本依据。
如果在上述的猜想中,令q=3,我们可以得到一个弱版本的曲面色临界图猜想:曲面S上是否存在无限多的k-色临界图。这个问题是由Dirac[13] 最先开始研究的。他观察到:对每个固定的曲面S,和每个固定的自然数k≥8,曲面S上仅有有限多个k-色临界图。Mohar和Thomassen[14] 证明了:对于亏格g ≥ 2的曲面S,曲面S上的7-色临界图的点数少于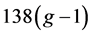 。Gallai[15] 给出了k-色临界图中所有度数为
。Gallai[15] 给出了k-色临界图中所有度数为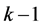 的点诱导子图的一个优美的刻画:k-色临界图中所有度数为
的点诱导子图的一个优美的刻画:k-色临界图中所有度数为 的点诱导出一个子图,它的块或者是奇圈或者是完全图。我们借助于Euler公式和Gallai所发展起来的研究色临界图的方法,改进了Mohar和Thomassen的这个结果,给出了曲面S上的7-色临界图的个数是有限的一个比较简洁的证明。除此以外,我们还给出曲面S上的每一个k-色临界图
的点诱导出一个子图,它的块或者是奇圈或者是完全图。我们借助于Euler公式和Gallai所发展起来的研究色临界图的方法,改进了Mohar和Thomassen的这个结果,给出了曲面S上的7-色临界图的个数是有限的一个比较简洁的证明。除此以外,我们还给出曲面S上的每一个k-色临界图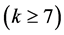 的点数上界的一个统一的表达式。
的点数上界的一个统一的表达式。
2. 主要定理及其证明
定理1.1:曲面S上的7-色临界图G的点数至多为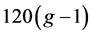 ,其中g ≥ 2。
,其中g ≥ 2。
证明:反证法。假定曲面S上的7-色临界图G有多于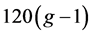 个点。Euler公式结合平均度的方法,可以推出对固定的曲面S和嵌入到S上一个足够大的图G,G一定有一个度数至多为6的点。事实上,由Euler公式可知,曲面嵌入图的边数
个点。Euler公式结合平均度的方法,可以推出对固定的曲面S和嵌入到S上一个足够大的图G,G一定有一个度数至多为6的点。事实上,由Euler公式可知,曲面嵌入图的边数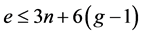 ,进而
,进而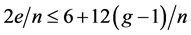 ,曲面S上的7-色临界图有多于
,曲面S上的7-色临界图有多于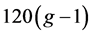 个点,所以G一定有一个度数至多为6的点。
个点,所以G一定有一个度数至多为6的点。
下证曲面S上的7-色临界图G有多于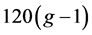 个点时,一定有一个6度点,使得这个6度点的6个邻点全是6度点且这个6度点关联的面全是三角形。
个点时,一定有一个6度点,使得这个6度点的6个邻点全是6度点且这个6度点关联的面全是三角形。
令v,e,f分别表示图G的点数、边数和面数, 表示度数为i的点数,
表示度数为i的点数,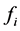 表示度数为i的面数。我们有
表示度数为i的面数。我们有![]() ,
,![]() 和
和![]() 成立。由Euler公式,
成立。由Euler公式,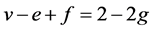 得
得
![]() 。
。
又因为曲面S上的7-色临界图G的所有点的度数均≥6。上式可以变形为
![]()
这个等式左边的两项均是非负的,有![]() 和
和![]() 成立。
成立。
先考查![]() ,将其展开,即
,将其展开,即
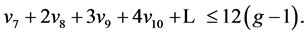
注意到
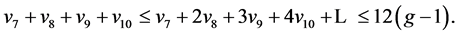
等号成立当且仅当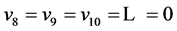 ,即不存在8度及其以上的点。
,即不存在8度及其以上的点。
由以上的分析知,
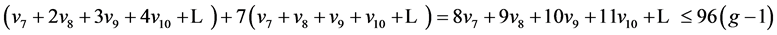
这个式子告诉我们,在曲面S上的7-色临界图G中所有的7度以上的点及其关联的点数至多为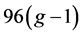 。而总点数
。而总点数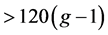 ,所以一定存在一个6度点,使得这个6度点的6个邻点全是6度点。.
,所以一定存在一个6度点,使得这个6度点的6个邻点全是6度点。.
再考查![]() 将其展开,即
将其展开,即
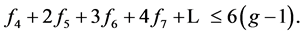
注意到

等号成立当且仅当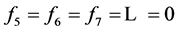 ,即不存在包含5个点以上的面。由以上的分析知,
,即不存在包含5个点以上的面。由以上的分析知,
 。
。
这个式子告诉我们,在曲面S上的7-色临界图G中所有的4度以上的面所覆盖的点至多为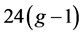 。而总点数
。而总点数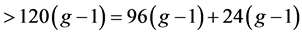 ,所以一定有一个6度点,使得这个6度点的6个邻点全是6度点且这个6度点关联的面全是三角形。
,所以一定有一个6度点,使得这个6度点的6个邻点全是6度点且这个6度点关联的面全是三角形。
因此v及其邻点属于由度数为6的点诱导子图中的一个块。因为这个块不是一个奇圈,所以它是一个完全图。进而G包含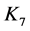 ,矛盾。这是因为一个7-色临界图不包含一个7-色临界图作为其真子图。证毕。
,矛盾。这是因为一个7-色临界图不包含一个7-色临界图作为其真子图。证毕。
曲面S上的7-色临界图有至多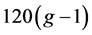 个点,也就是说曲面S上的7-色临界图的个数是有限的。因此理论上我们可以设计一个多项式算法,来检验一个给定的曲面嵌入图是否有6-着色。对于一般可定向曲面上的k-色临界图,我们下面的定理给出了曲面
个点,也就是说曲面S上的7-色临界图的个数是有限的。因此理论上我们可以设计一个多项式算法,来检验一个给定的曲面嵌入图是否有6-着色。对于一般可定向曲面上的k-色临界图,我们下面的定理给出了曲面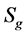 上的每一个k-色临界图
上的每一个k-色临界图 的点数上界的一个统一的表达式。
的点数上界的一个统一的表达式。
定理1.2:曲面Sg 上的每一个k-色临界图的点数不超过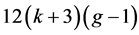 ,其中
,其中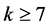 ,g > 2。
,g > 2。
证明:记n,e,f分别为图G的边数、点数和面数, 为度数为k的点数,由Euler公式
为度数为k的点数,由Euler公式 ,有
,有
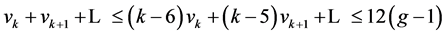 ,
,
进而
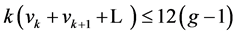 。
。
由
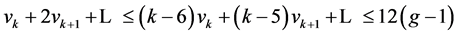 ,
,
得,
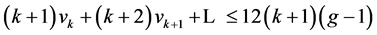 ,
,
进而,
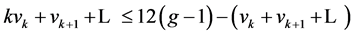 。
。
由以上的分析知,图G中所有度数大于k的点和它们的邻域中的点数总和至多是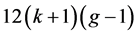 。
。
如果设图的点数上界为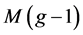 ,即,有一个
,即,有一个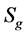 上的k-临界图的点数超过
上的k-临界图的点数超过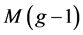 。那么重复前面关于面的处理过程后可知:图中被度数大于3的面所覆盖的点数至多是
。那么重复前面关于面的处理过程后可知:图中被度数大于3的面所覆盖的点数至多是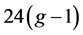 。于是,图中被三角形所覆盖(同时没有被面数大于3的面所覆盖)的点集合B的阶数大于
。于是,图中被三角形所覆盖(同时没有被面数大于3的面所覆盖)的点集合B的阶数大于 。所以,图G当中所有度数为
。所以,图G当中所有度数为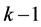 ,且其邻域的点(没有被度数大于
,且其邻域的点(没有被度数大于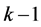 的点及其领域覆盖)的全体A的阶数大于
的点及其领域覆盖)的全体A的阶数大于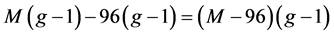 。只要M适当地大,即
。只要M适当地大,即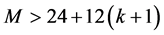 ,那么这两个集合A,B的交集
,那么这两个集合A,B的交集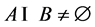 。 于是存在一点
。 于是存在一点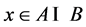 ,使得
,使得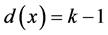 ,而且x被三角形所覆盖,同时其领域中的点都是
,而且x被三角形所覆盖,同时其领域中的点都是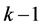 度点:
度点: 。不妨设这个次序就是它们在嵌入方案中的局部旋转次序。容易看出,这k个点
。不妨设这个次序就是它们在嵌入方案中的局部旋转次序。容易看出,这k个点 诱导出图的一个完全子图
诱导出图的一个完全子图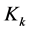 ,它是图G的一个真子图。这与G是k-色临界图相违背。证毕。
,它是图G的一个真子图。这与G是k-色临界图相违背。证毕。
图G和图H的联图G+H是由图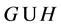 添加图G和图H的所有点之间的边得到的图。如果
添加图G和图H的所有点之间的边得到的图。如果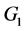 和
和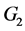 是有公共点
是有公共点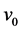 ,和
,和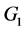 中的一条边
中的一条边![]() 和
和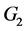 中的一条边
中的一条边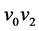 的图,由这两个图经过Hajós构造得到的图是指是具有顶点集
的图,由这两个图经过Hajós构造得到的图是指是具有顶点集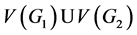 和边集
和边集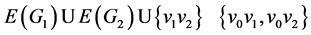 的图。Thomassen[16] 证明了:环面上的嵌入图是可5-着色的,除非它包含
的图。Thomassen[16] 证明了:环面上的嵌入图是可5-着色的,除非它包含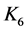 ,六个点的完全图,或者
,六个点的完全图,或者 ,长度为3和5的两个圈的联图,或者
,长度为3和5的两个圈的联图,或者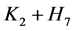 ,
,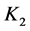 和
和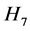 的联图,其中
的联图,其中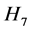 是由在
是由在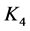 的两个拷贝上应用Hajós构造得到的,或者环面上有11个点的三角剖分图
的两个拷贝上应用Hajós构造得到的,或者环面上有11个点的三角剖分图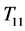 ,它是由长度为11的圈添加圈上的距离为2和3点之间的边得到的图。Chenette,Postle,Streib,Thomas和Yerger[17] 使用上述Thomassen所发展起来的方法,给出了Klein瓶上的6-色临界图完全列表。Kawarabayashi,Král,Kynčl和Lidický[18] 借助于计算机也得到了Klein瓶上的6-色临界图完全列表。
,它是由长度为11的圈添加圈上的距离为2和3点之间的边得到的图。Chenette,Postle,Streib,Thomas和Yerger[17] 使用上述Thomassen所发展起来的方法,给出了Klein瓶上的6-色临界图完全列表。Kawarabayashi,Král,Kynčl和Lidický[18] 借助于计算机也得到了Klein瓶上的6-色临界图完全列表。
使用Hajós构造,我们可以很容易地找到某个固定曲面上的一些k-色临界图。但是要找到某个固定曲面上的所有的色临界图是一件很困难的事。到目前为止,仅知道射影平面、环面和Klein瓶这三个小亏格曲面上6-色临界图的确切数目。
项目基金
国家自然科学基金项目(11171114)。
参考文献 (References)
- Möbius, A.F. (1861) Zur theorie der polyëder und elementarverwandtschaft. Qeuvres Complètes, 2, 519-559.
- Jordan, C. (1866) Sur la déormation des surfaces. Journal de Mathématiques Pures et Appliquées, 11, 105-109.
- Thomassen, C. (1992) The Jordan-Schönflies theorem and the classification of surfaces. The American Mathematical Monthly, 99, 116-130.
- Euler, L. (1752) Elementa doctrinae solidorum. Demonstratio nonnullarum insignium proprietatum. Novi Comment Acad. Sc. Imp. Petropol., 4, 109-160.
- Edmonds, J.R. (1960) A combinatorial representation for polyhedral surfaces. Notices of the AMS—American Mathematical Society, 7, 646.
- Heffter, L. (1891) Über das problem der nachbargebiete. Mathematische Annalen, 38, 477-508.
- Heawood, P.J. (1890) Map colour theorem. The Quarterly Journal of Pure and Applied Mathematics, 24, 332-338.
- Ringel, G. and Youngs, J.W.T. (1968) Solution of the Heawood map-coloring problem. Proceedings of the National Academy of Sciences of the USA, 60, 438-455.
- Franklin, P. (1934) A six color problem. Journal of Mathematical Physics, 13, 363-369.
- Dirac, G.A. (1952) Map color theorem. Canadian Journal of Mathematics, 4, 480-490.
- Albertson, M.O. and Hutchinson, J.P. (1977) The independence ratio and genus of a graph. Transactions of the American Mathematical Society, 226, 161-173.
- Gimbel, J. and Thomassen, C. (1997) Coloring graphs with fixed genus and girth. Transactions of the American Mathematical Society, 349, 4555-4564.
- Dirac, G.A. (1953) The coloring of maps. Journal of the London Mathematical Society, 28, 476-480.
- Mohar, B. and Thomassen, C. (2001) Graphs on surfaces. Johns Hopkins University Press, London.
- Gallai, T. (1963) Kritische graphen I, II. Publications of the Mathematical Institute of the Hungarian Academy of Sciences, 8, 165-192,373-395.
- Thomassen, C. (1994) Five-coloring graphs on the torus. Journal of Combinatorial Theory, Series B, 62, 11-33.
- Chenette, N., Postle, L., Streib, N. and Thomas, R. (2012) Five-colorings graphs on the Klein bottle. Journal of Combinatorial Theory, Series B, 102, 1067-1098.
- Kawarayabashi, K.I., Král, D., Kynčl, J. and Lidický, B. (2009) 6-critical graphs on the Klein bottle. SIAM Journal on Discrete Mathematics, 23, 372-383.