Advances in Applied Mathematics
Vol.3 No.03(2014), Article ID:13995,6 pages
DOI:10.12677/AAM.2014.33019
Qualitative Analysis of a Stochastic SIR Epidemic Model with Saturated Incidence Rates
1Tongren Polytechnic College, Tongren
2Institute of Applied Mathematics, South-China Agricultural University, Guangzhou
Email: 553129685@qq.com
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: May 15th, 2014; revised: Jun. 18th, 2014; accepted: Jun. 25th, 2014
ABSTRACT
A stochastically mathematical model of a stochastic SIR epidemic model with saturated incidence rates is proposed and analyzed, setting that all the death rate and incident rate are similarly perturbed by an independent Gaussian white noise. First the paper shows that the infective population and recovered individuals will tend to zero exponentially almost surely under some additional condition. In addition, a sufficient condition for the stationary distribution around the endemic infection equilibrium state of the corresponding deterministic model is derived and the solution is ergodic.
Keywords:Epidemic Model, Saturated Incidence Rates, Gaussian White Noise, Stationary Distribution

具有饱和感染率的随机SIR传染病模型
的性质分析
谭 杨1,郭子君2
1铜仁职业技术学院,铜仁
2华南农业大学应用数学研究所,广州
Email: 553129685@qq.com
收稿日期:2014年5月15日;修回日期:2014年6月18日;录用日期:2014年6月25日

摘 要
建立了一类具有饱和感染率的随机SIR模型,假设易感者、感染者及移出者三群体的自然死亡率和疾病感染率分别受到相互独立的高斯白噪声干扰。首先证明了在一定的条件下,感染者与移出者种群将依指数趋于灭绝。再就是相应确定性系统的地方病平衡点存在时,得到了该随机系统围绕该点具有稳定的分布且该分布是遍历的充分条件。
关键词
传染病模型,饱和感染率,高斯白噪声,稳定分布

1. 引言
用数学建模的方法研究传染病的传播有助于描述传染病的发展和预测其变化趋势,为人们制定有效的预防策略提供了理论依据。现实中,很多传染病的传播效率常常受到时间上的波动,如麻疹、水痘等的疾病的感染率随着季节性的周期变化而变化[1] 。因此,传染病数学模型中引入周期因素更能精确揭示疾病传播的规律。文献[2] 研究了一类具有常数出生率的SIR传染病模型,并证明了模型周期解的存在性。文献[3] 研究了一类非自治SIR传染病模型周期解。
然而在现实情况中,生物种群的发展(疾病病菌的传播)不可避免地受到环境随机因素的干扰,并且这样的干扰在很多情况下不能被忽略,对某些实际过程的分析有必要从通常的确定性观点转到随机的观点[4]
。文献[5] 建立了一类随机SIR模型及具有分布时滞的模型,假设模型中的感染率系数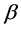 受到白噪声的干扰:
受到白噪声的干扰: ,
, 表示维纳过程,得出了系统稳定的条件。文献[6]
研究了文献[5] 的模型,得出了保证平衡点稳定性更好的条件。文献[7] 建立了HIV内部病毒感染CD4受体细胞的随机动力模型,得到了易感细胞具有稳定分布和感染细胞与病毒灭绝的充分条件。文献[8]
研究了一类捕食者带有疾病的随机食饵-捕食者模型,得到了随机系统围绕确定性系统的地方病平衡点具有稳定分布的充分条件。文献[9] 提出了如下具有饱和感染率的时滞SIR模型:
表示维纳过程,得出了系统稳定的条件。文献[6]
研究了文献[5] 的模型,得出了保证平衡点稳定性更好的条件。文献[7] 建立了HIV内部病毒感染CD4受体细胞的随机动力模型,得到了易感细胞具有稳定分布和感染细胞与病毒灭绝的充分条件。文献[8]
研究了一类捕食者带有疾病的随机食饵-捕食者模型,得到了随机系统围绕确定性系统的地方病平衡点具有稳定分布的充分条件。文献[9] 提出了如下具有饱和感染率的时滞SIR模型:
 (1)
(1)
其中,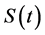 为易感种群数量,
为易感种群数量,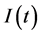 为已感染种群数量,
为已感染种群数量,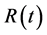 表示移出类种群数量,
表示移出类种群数量, 为常数补充率或出生率,
为常数补充率或出生率,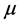 为自然死亡率,
为自然死亡率,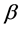 为接触系数,
为接触系数, 为因病死亡率,
为因病死亡率,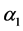 与
与 表示易感种群与感染种群对传染系
表示易感种群与感染种群对传染系
数产生的抑制效应,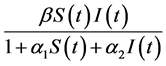 整体项表示饱和感染率(函数)。
整体项表示饱和感染率(函数)。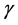 为康复率,
为康复率, 表示易感者染上疾
表示易感者染上疾
病后的潜伏期。文献[10] 提出的模型,是在模型(1)的基础上,不考虑率时滞因素,即认为 ;且接触系数
;且接触系数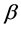 为有正的上、下界的周期函数
为有正的上、下界的周期函数 ,即
,即
 (i.e.
(i.e.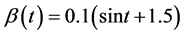 )研究了如下随机系统的渐近性质:
)研究了如下随机系统的渐近性质:
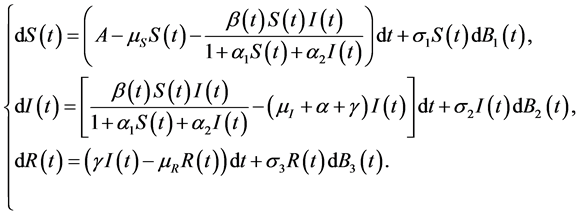 (2)
(2)
本文假设种群之间的部分作用系数受到随机因素的干扰,在模型(1)的基础上,令时滞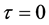 ,考虑不同于模型(2)且更全面的随机干扰因素:
,考虑不同于模型(2)且更全面的随机干扰因素:
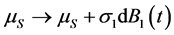 ,
,
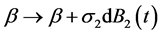 ,
,
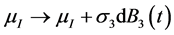 ,
,
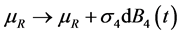 得到如下模型:
得到如下模型:
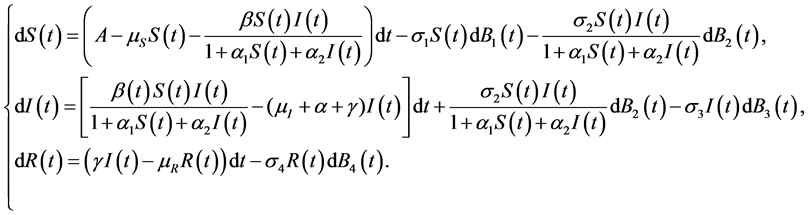 (3)
(3)
其中,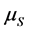 、
、 、
、 分别为
分别为 、
、 、
、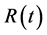 的自然死亡率,
的自然死亡率, ,
, 为白噪声的干扰强度,
为白噪声的干扰强度,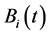 ,
,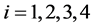 为相互独立的标准布朗运动。其他系数与模型(1)中一致,各系数均非负。
为相互独立的标准布朗运动。其他系数与模型(1)中一致,各系数均非负。
本文中, 表示具有滤子
表示具有滤子 的完备概率空间,且满足通常的条件(如
的完备概率空间,且满足通常的条件(如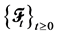 右连续且
右连续且 包含所有的零测度集)。对于
包含所有的零测度集)。对于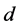 维的随机微分方程[11]
维的随机微分方程[11]
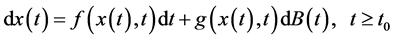 .
.
设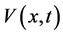 为定义在
为定义在 上的函数,对
上的函数,对 至少二阶连续可微和对
至少二阶连续可微和对 至少一阶连续可微。算子
至少一阶连续可微。算子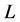 定义为
定义为
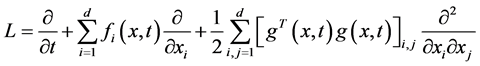 (4)
(4)
将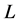 作用到函数
作用到函数 上,则
上,则
 .
.
2. 随机模型(3)的解的存在、唯一性
可以看出,模型(3)满足局部Lipschitz条件,由文献[12] 可知,对任意给定的初值 ,方程存在唯一的局部正解
,方程存在唯一的局部正解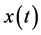 ,
, ,其中
,其中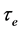 是爆炸时。事实上,可用文献[4]
的方法证明模型(3)的该局部解是全局的。
是爆炸时。事实上,可用文献[4]
的方法证明模型(3)的该局部解是全局的。
3. 随机系统(3)关于点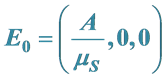 的渐近性质
的渐近性质
容易看出,点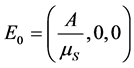 是确定性系统(2)无病平衡点,但不是相应随机系统(3)的无病平衡点。在传染病动力性的研究当中,无病平衡点的稳定性表明了系统中的传染病终究会灭绝,对研究系统中种群与疾病的发展规律有重要的作用。本节研究随机系统(3)关于点
是确定性系统(2)无病平衡点,但不是相应随机系统(3)的无病平衡点。在传染病动力性的研究当中,无病平衡点的稳定性表明了系统中的传染病终究会灭绝,对研究系统中种群与疾病的发展规律有重要的作用。本节研究随机系统(3)关于点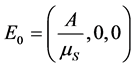 的渐近性质。
的渐近性质。
定理1 设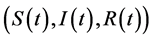 是模型(3)的解,初值为
是模型(3)的解,初值为 。若条件:
。若条件:
1) ,
,
2) ,
,
均成立,则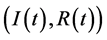 依指数几乎处处趋于
依指数几乎处处趋于 。其中
。其中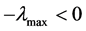 为如下负定矩阵
为如下负定矩阵
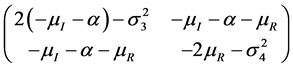
的最大(负)特征值。
证明 由模型(3)可知
 设
设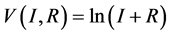 ,则由
,则由 引理有
引理有
 因为
因为
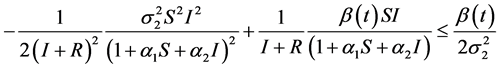 则有
则有
 .
.
上式中的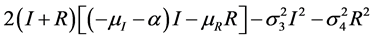 可改写为
可改写为
 .
.
则

对于矩阵
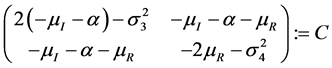 若
若

成立,则矩阵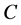 为负定矩阵,即存在
为负定矩阵,即存在 使得
使得
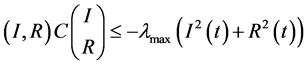 .
.
因此有
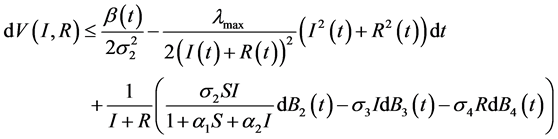 , (5)
, (5)
又 ,则
,则
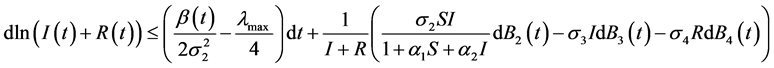 .
.
对上式两边积分可得
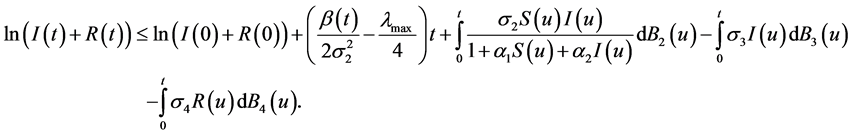
又由文献[11] 可知,

当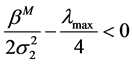 时有
时有
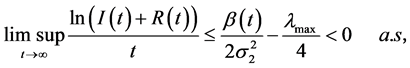 (6)
(6)
即当 时,
时, 且
且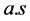
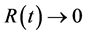 。证毕。
。证毕。
4. 随机系统(3)关于点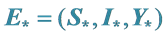 的分布稳定性
的分布稳定性
由文献[10] 可知,当 时,确定性系统(1)存在地方病平衡点
时,确定性系统(1)存在地方病平衡点 ,其中
,其中
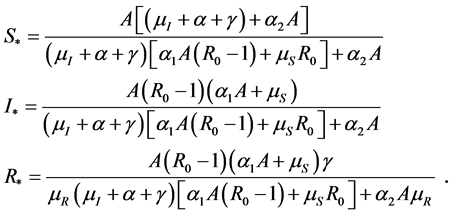
而该点并不是随机系统(3)的平衡点。本节研究系统(3)关于点 的渐近性质。
的渐近性质。
定理2 设 成立,
成立, 是模型(3)的解,初值为
是模型(3)的解,初值为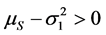 ,
, ,
, ,且
,且 时,随机系统(3)存在一稳定分布且该分布遍历。
时,随机系统(3)存在一稳定分布且该分布遍历。
其中, ,
, 。
。
证明 定义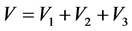 ,其中,
,其中,
 ,
,
 ,
,
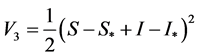 ,
,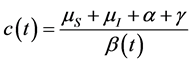 .
.
由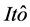 引理有
引理有
 (7)
(7)
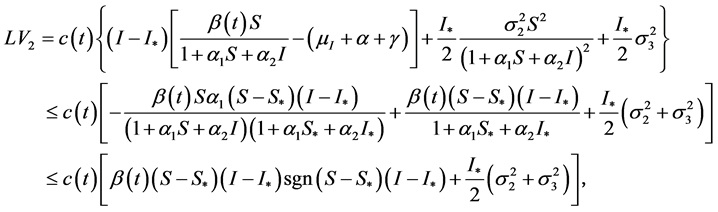 (8)
(8)
 (9)
(9)
令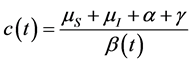 ,且结合基本不等式有
,且结合基本不等式有
 (10)
(10)
令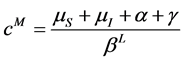 ,
, ,当
,当
 且
且
 (11)
(11)
时,可知椭球
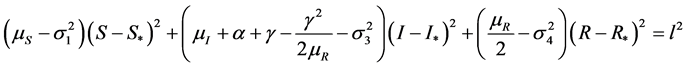
整体在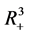 内部。
内部。
则由文献[12] 的引理4.1和定理4.1可知本定理成立。证毕。
参考文献 (References)
- [1] Hethcote, H.W. and Levin, S.A. (1989) Periodicity in epidemiological models. In: Applied Mathematical Ecology, Springer-Verlag, Berlin.
- [2] Hu, X.L. (2007) The existence of periodic solutions for a SIR epidemic model with constant birth rate. Pure and Applied Mathematics, 23, 372-376, 380.
- [3] Bai, Z. and Zhou, Y. (2011) Existence of two periodic solutions for a non-autonomous SIR epidemic model. Applied Mathematical Modelling, 35, 382-391.
- [4] Mao, X.R., Marion, G. and Renshaw, E. (2002) Environmental Brownian noise suppresses explosions in population dynamics. Stochastic Processes and their Application, 97, 95-110.
- [5] Tornatore, E., Buccellato, V. and Shaikhet, L. (2012) Stability of a stochastic SIR system. Physica A, 354, 111-126.
- [6] Ji, C.Y., Jiang, D.Q. and Shi, N.Z. (2010) The behavior of an SIR epidemic model with stochastic perturbation. Stochastic Analysis and Applications, 30, 121-131.
- [7] Dalal, N., Greenhalgh, D. and Mao, X.R. (2008) A stochastic model for internal HIV dynamics. Mathematical Analysis and Applications, 341, 1084-1101.
- [8] Li, S. and Zhang, X. (2013) Qualitative analysis of a stochastic predator-prey system with disease in the predator. International Journal of Biomathematics, 6, 12500681-125006813.
- [9] Abta, A., Kaddar, A. and Alaoui, H.T. (2012) Global stability for delay SIR and SEIR epidemic models with saturated incidence rates. Electronic Journal of Differential Equations, 23, 1-13.
- [10] Liu, Z.J. (2013) Dynamics of positive solutions to SIR and SEIR epidemic models with saturated incidence rates. Nonlinear Analysis: Real World Applications, 14, 1286-1299.
- [11] Lahrouz, A. and Omari, L. (2013) Extinction and stationary distribution of a stochastic SIRS epidemic model with non-linear incidence. Statistics & Probability Letters, 83, 960-968.
- [12] Mao, X.R. (1997) Stochastic differential equation and applications. Horwood Publishing Limited, Chichester.