Advances in Applied Mathematics
Vol.3 No.04(2014), Article ID:14177,4 pages
DOI:10.12677/AAM.2014.34023
Generalization of Deng’s Pseudo-Metric on the Lattices
1Mathematics and Statistics Institute, Henan University of Science and Technology, Luoyang
2College of Applied Science, Beijing University of Technology, Beijing
Email: *chenpengbeijing@sina.com
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Mar. 2nd, 2014; revised: Sep. 12th, 2014; accepted: Sep. 29th, 2014
ABSTRACT
In this paper, we research some properties of Deng’s pseudo-metric, and show an
equivalent form of its axioms. Therefore, we generalize Deng’s pseudo-metric from
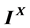 to completely distributive lattice
to completely distributive lattice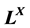 。
。
Keywords:Deng’s Pseudo-Metric; Shi’s Pseudo-Metric, Fuzzy Point,
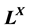 Completely Distributive Lattice
Completely Distributive Lattice

Deng式伪度量在格上的推广
陈 鹏1,2*,郭飞飞1
1河南科技大学,数学与统计学院,洛阳
2北京工业大学,应用数理学院,北京
Email: *chenpengbeijing@sina.com
收稿日期:2014年3月2日;修回日期:2014年9月12日;录用日期:2014年9月29日

摘 要
本文研究了Deng式伪度量的一些性质,并给出了它的一种等价形式,由此把定义在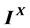 上的Deng式伪度量推广到完全分配格
上的Deng式伪度量推广到完全分配格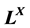 上。
上。
关键词
Deng伪度量,Shi伪度量,模糊点;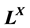 完全分配格
完全分配格

1. 引言和预备
格上度量是格上拓扑学研究的重要内容,国外Erceg M.A.在上世纪70年代末给出了较经典的Erceg度量,得到了许多较满意结果[1] ,是无点派的优秀成果;国内邓自克教授上世纪八十年代初提出Deng度量,该度量是国内最早且较系统地研究过的度量,邓曾给出过该度量较漂亮的结果[2]
,是有点派的典范之一,但Deng度量是在 这种特殊格上定义且是通过下列模糊点定义的,即
这种特殊格上定义且是通过下列模糊点定义的,即
定义1.1 一个模糊点 当且仅当
当且仅当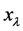 是被定义如下[2] :
是被定义如下[2] :
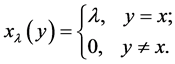
这里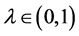 。简记映射
。简记映射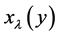 为
为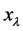 ,同时,
,同时,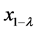 被称为
被称为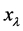 的余点。
的余点。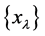 表示
表示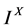 在所有模糊点的集合。
在所有模糊点的集合。
在文[3] [4] [5] 中,刘应明院士与王国俊教授分别对下列模糊点和重域(或远域)(参考后面预备知识)的合理性进行了论证,由此在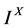 上现大家广泛接受的模糊点是下列定义1.2,即
上现大家广泛接受的模糊点是下列定义1.2,即
定义1.2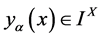 是一个模糊点,当且仅当
是一个模糊点,当且仅当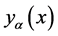 被定义如下[3] [4] [5] :
被定义如下[3] [4] [5] :
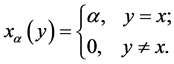
尽管在文[2] 中,邓借助余点的邻域给出过该度量较好的结论。但由于Deng度量是建立在比较特殊的格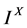 与特殊的模糊点上,特别是邓给出的该度量公理体系在格上推广非常困难,这极大的局限了该度量的接受。
与特殊的模糊点上,特别是邓给出的该度量公理体系在格上推广非常困难,这极大的局限了该度量的接受。
在文[6] 我们证明了Deng度量一定是Erceg度量,但反之不成立。并证明了Deng度量所诱导拓扑和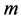 -一致结构就是Erceg度量诱导拓扑和Hutton一致结构。本文在此基础上,给出了Deng度量的一组等价公理,由此把定义在
-一致结构就是Erceg度量诱导拓扑和Hutton一致结构。本文在此基础上,给出了Deng度量的一组等价公理,由此把定义在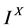 上的Deng式伪度量很自然地推广到完全分配格
上的Deng式伪度量很自然地推广到完全分配格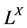 上。
上。
为此本文需要下列预备知识:
定义1.3 一个映射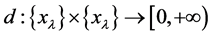 被称为Deng伪度量,如果它满足下列条件[2] :
被称为Deng伪度量,如果它满足下列条件[2] :
1) 如果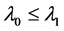 ,则
,则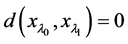 ;
;
2)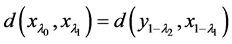 ;
;
3) ;
;
4)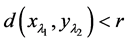 ,这里
,这里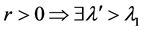 使得
使得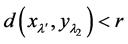 。
。
定义1.4 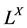 上的Shi伪度量是一个满足下列条件的
上的Shi伪度量是一个满足下列条件的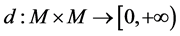 映射[7] :
映射[7] :
(N1)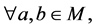 如果
如果 ,那么
,那么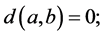
(N2)
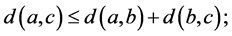
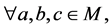
(N3)
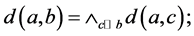
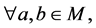
(N4)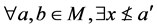
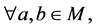 使得
使得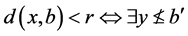 使得
使得 。
。
注 (N4)是等价于下列条件
(N4)*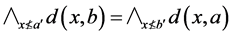
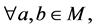 。
。
定理1.5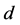 是一个Deng伪度量,如
是一个Deng伪度量,如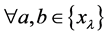 ,有
,有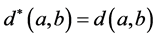 ,且令
,且令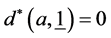 和
和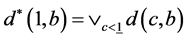 那么
那么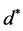 在
在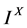 上是一个Shi伪度量[6]
。
上是一个Shi伪度量[6]
。
定义1.6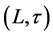 是格上拓扑空间。1) 对
是格上拓扑空间。1) 对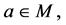 称
称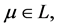 是
是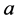 的重域,若有开集
的重域,若有开集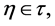 使得
使得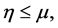 且
且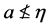 ;2)
;2)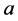 的重域族
的重域族 称为
称为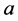 的
的 基,若对
基,若对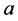 的任一重域
的任一重域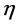 ,存在
,存在 使得
使得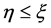 ;3)
;3)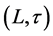 称为是
称为是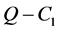 的,若对每一个
的,若对每一个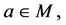 有可数
有可数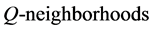 基[8]
。
基[8]
。
2. 其它预备知识
本文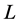 表一个具有逆序对合对应“
表一个具有逆序对合对应“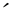 ”的完全分配格。
”的完全分配格。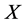 是指标集,
是指标集,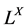 是从
是从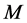 到
到 的全部映射组成的集,且带有点式地被定义
的全部映射组成的集,且带有点式地被定义 和
和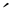 并按映射的大小顺序构成的一个偏序集。
并按映射的大小顺序构成的一个偏序集。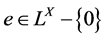 被叫一个分子,当且仅当对
被叫一个分子,当且仅当对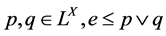 蕴含
蕴含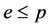 或
或 ,
,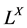 的全部分子集记为
的全部分子集记为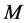 。分子
。分子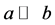 表
表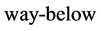 关系。
关系。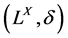 是
是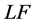 拓扑空间,
拓扑空间,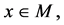
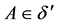 (即
(即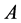 为闭集)。如
为闭集)。如 则称
则称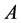 为
为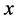 的闭远域,
的闭远域,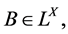 如果
如果 有闭远域
有闭远域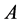 使
使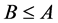 ,则称
,则称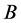 为
为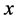 的远域。其他未声明概念与符号请参考文[5]
。
的远域。其他未声明概念与符号请参考文[5]
。
3. 本文主要结果
为了推广Deng度量,首先我们证明Deng度量定义可以由下列定理中的(M1) - (M4)代替。
定理3.1 一个映射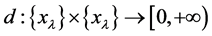 是Deng伪度量当且仅当它满足下列条件:
是Deng伪度量当且仅当它满足下列条件:
(M1) 如果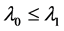 ,则
,则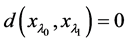 ;
;
(M2)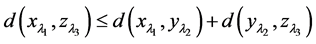 ;
;
(M3)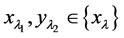 ,
,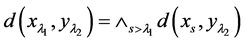 ;
;
(M4)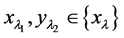 ,
, ,使得
,使得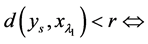
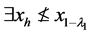 使得
使得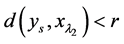 。
。
为证明定理3.1,我们需要证明下列一些引理,这些引理也是该度量的性质的进一步研究。
引理3.1 设 映射满足(I)、(III)和(IV),则(M3)成立。
映射满足(I)、(III)和(IV),则(M3)成立。
证明 由于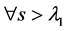 根据(I)和(III)得
根据(I)和(III)得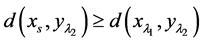 ,从而
,从而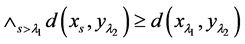 。
。
假设 ,则
,则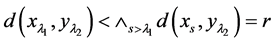 ,根据(IV),
,根据(IV),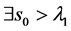 使得
使得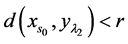 而
而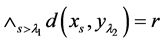 知
知 有
有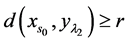 ,从而矛盾,命题得证。
,从而矛盾,命题得证。
引理3.2 设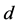 映射满足(M3)
映射满足(M3)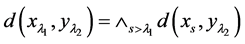 ,则(IV)成立。
,则(IV)成立。
证明 证明显然。
推论3.3 设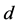 映射满足(I)和(III),则(IV)
= (M3)。
映射满足(I)和(III),则(IV)
= (M3)。
证明 由引理3.1和引理3.2,结论显然。
引理3.4 设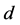 映射满足(I)、(III)、(IV)和(M4),则(II)成立。
映射满足(I)、(III)、(IV)和(M4),则(II)成立。
证明 取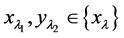 ,根据(I)和(III)得
,根据(I)和(III)得
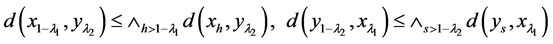 。
。
由于(N4)*Û(M4),由(N4)*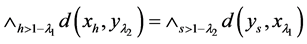 和引理3.2得:
和引理3.2得:
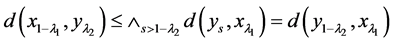 。
。
同理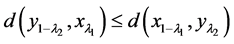 。由上得
。由上得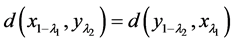 。从而(II)成立,即命题得证。
。从而(II)成立,即命题得证。
推论3.5 设d映射满足(I)、(III)、(IV),则(II) = (M4)成立。
证明 先证明(I) + (III) + (IV) + (II)Þ(M4)成立(由于(N4)*Û(N4)Û(M4))。
证(M4)成立,只需要证明(N4)*成立,设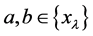 ,因为
,因为
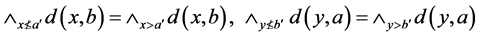 ,
,
所以须证
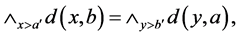
由于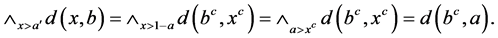
同理可证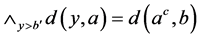 。根据(II),能知有
。根据(II),能知有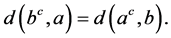 因此(N4)*成立。
因此(N4)*成立。
其次有引理3.4 (I) + (III) + (IV) + (M4)Þ(II)成立。
定理3.1的证明 (M1)Û(I),(M2)Û(III),由推论3.3得(M3)Û(IV),再由推论3.5得(II)Û(M4),从而该命题结论成立。
定理3.2 设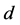 是一个映射,满足(N3)和(II),则(IV)成立。
是一个映射,满足(N3)和(II),则(IV)成立。
证明 取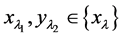 ,由(N3)和(II)得
,由(N3)和(II)得
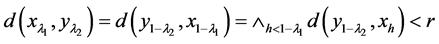 .
.
从而可知 使得
使得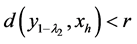 ,再由(II)得
,再由(II)得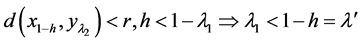 ,得
,得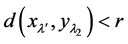 即(IV)成立。
即(IV)成立。
由于Deng度量是建立在比较特殊的模糊点上,且邓自克教授给出的公理也不好推广,这局限了该度量的使用和接受,现有了定理3.1,Deng度量很自然从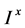 到
到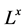 完全分配格上可做如下推广:
完全分配格上可做如下推广:
定义3.8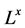 上的Deng伪度量是一个满足下列条件的
上的Deng伪度量是一个满足下列条件的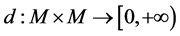 映射:
映射:
(L1)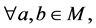 如果
如果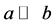 ,那么
,那么
(L2)
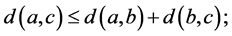
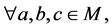
(L3)
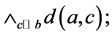
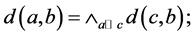
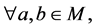
(L4)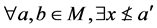
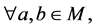 使得
使得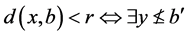 使得
使得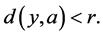
这么推广的好处:第一:Deng度量在更加广泛的 完全分配格上进行研究;第二:推广的Deng度量与Shi度量比较,两者仅仅(N3)与(L3)不同(Erceg度量一样,参考文[9]
),从而,根据使用不同连续性公理,得到三种Erceg度量,Den度量,Shi度量;第三,根据文[6] [9] 结论,尽管三种度量不同,但地位平行,它们之间既有联系又有差别,从诱导拓扑性质来看,
完全分配格上进行研究;第二:推广的Deng度量与Shi度量比较,两者仅仅(N3)与(L3)不同(Erceg度量一样,参考文[9]
),从而,根据使用不同连续性公理,得到三种Erceg度量,Den度量,Shi度量;第三,根据文[6] [9] 结论,尽管三种度量不同,但地位平行,它们之间既有联系又有差别,从诱导拓扑性质来看, 上Deng度量性质优于Erceg度量和Shi度量,且根据定理1.5知:在
上Deng度量性质优于Erceg度量和Shi度量,且根据定理1.5知:在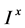 上Deng度量所诱导的拓扑就是Shi度量诱导的拓扑,从而在
上Deng度量所诱导的拓扑就是Shi度量诱导的拓扑,从而在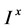 上Deng度量是
上Deng度量是 的。
的。
参考文献 (References)
- [1] Erceg, M.A. (1979) Metric spaces in fuzzy set theory. Journal of Mathematical Analysis and Applications, 69, 205- 230.
- [2] Deng, Z.K. (1982) Fuzzy pseudo-metric spaces. Journal of Mathematical Analysis and Applications, 86, 74-79.
- [3] Pu, B.M. and Liu, Y.M. (1980) Fuzzy Topology I, neighborhood structure of a fuzzy point and Moore-Smith Convergence. Journal of Mathematical Analysis and Applications, 76, 571-599.
- [4] 王国俊 (1982) 领域方法在Fuzzy拓扑学中的困难. 模糊数学, 1, 113-116.
- [5] Wang, G.J. (1988) Theory of L-fuzzy topological space. Shanxi Normal University Publishers, Xian. (In Chinese).
- [6] 陈鹏 (2008) L-拓扑中几种度量的性质及其关系. 博士论文, 北京理工大学, 北京.
- [7] Shi, F.G. (2001) Pointwise pseudo-metrics in L-fuzzy set theory. Fuzzy Sets and Systems, 121, 200-216.
- [8] 梁基华 (1984) 关于不分明度量空间的几个问题. 数学年刊, 1, 59-67.

NOTES
*通讯作者。