Dynamical Systems and Control
Vol.05 No.04(2016), Article ID:18784,8
pages
10.12677/DSC.2016.54015
Information Geometry and Control Theory
Xiwu Han1, Huafei Sun1, Zhenning Zhang2
1School of Mathematics and Statistics, Beijing Institute of Technology, Beijing
2College of Applied Sciences, Beijing University of Technology, Beijing

Received: Sep. 30th, 2016; accepted: Oct. 21st, 2016; published: Oct. 25th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, we first introduce briefly the fundamental contents of information geometry. By introducing the Fisher information matrix and the dual connections, we can deal with the statistical manifold. At the same time, by using the theory of Lie groups and submanifolds of the general linear group, the theory of matrix information geometry is constructed. Then we introduce the applications of information geometry to control theory, including the random case and the non- random case.
Keywords:Information Geometry, Matrix Information Geometry, Fisher Information Matrix, Lie Group

信息几何与控制理论
韩希武1,孙华飞1,张真宁2
1北京理工大学数学与统计学院,北京
2北京工业大学数理学院,北京

收稿日期:2016年9月30日;录用日期:2016年10月21日;发布日期:2016年10月25日

摘 要
本文首先简要介绍信息几何的基本内容,包含随机的情形和非随机的情形。通过引入Fisher信息矩阵、对偶联络的引入,来处理随机的统计流形;通过利用一般线性群的李子群以及子流形的理论,建立矩阵信息几何理论。然后介绍信息几何在控制理论中的应用,包含随机的情形和非随机的情形。
关键词 :信息几何,矩阵信息几何,Fisher信息矩阵,Lie群

1. 引言
信息几何旨在利用黎曼几何的方法来解决信息领域里的问题。经过多年的研究,信息几何的理论体系不断完善,所涉及的范围愈加广泛。特别是,随着信息几何的理论在统计推断、神经网络、纠错码、雷达信号处理、图像处理、控制理论等领域的成功应用 [1] - [9] ,信息几何受到越来越多的关注。一方面,许多学者试图把各种数学工具引入到信息几何的框架,另一方面越来越多的学者在尝试信息几何能不能用来解决自己研究领域的问题。当然,信息几何的理论不是万能的,它的适用范围也是有条件的。究竟什么研究领域能够利用信息几何来解决,需要不断的尝试。经过多年的研究人们发现信息几何主要分为两种体系:随机的信息几何与非随机的信息几何。通过引入Fisher信息矩阵作为黎曼度量把要研究的对象看成黎曼流形,再引入对偶联络和Kullback-Leibler散度,由此建立起随机的信息几何理论框架。对于非随机的情形,主要利用一般线性群的李子群和子流形的理论来构建信息几何的理论,其中所涉及到的几何与拓扑等理论,使得信息几何的面貌焕然一新,随之而来的利好是应用范围迅速扩大,特别是在核磁共振等领域的应用令人振奋。
本文我们首先介绍信息几何的基本内容,然后介绍信息几何在控制领域中的应用。
2. 黎曼几何
微分流形是一个带有拓扑结构和微分结构的集合,在其上面可以进行求导和积分等运算。例如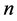 维欧几里得空间
维欧几里得空间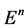 、
、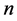 维球面
维球面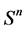 以及一般线性群
以及一般线性群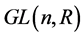 都是微分流形。
都是微分流形。 是平坦的空间,其上面连接任意两点的最短线是直线。对于一般的微分流形,其上面连接任意两点的最短线就不一定是直线了,例如球面
是平坦的空间,其上面连接任意两点的最短线是直线。对于一般的微分流形,其上面连接任意两点的最短线就不一定是直线了,例如球面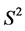 上连接其上面任意两点的最短线是大圆的一部分。设
上连接其上面任意两点的最短线是大圆的一部分。设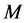 是一个
是一个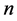 维流形,其上面每一点
维流形,其上面每一点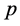 处的切空间
处的切空间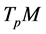 是一个线性空间。在
是一个线性空间。在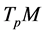 上可以定义黎曼度量
上可以定义黎曼度量
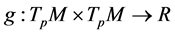
这是一个双线性的对称映射。于是,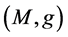 成为黎曼流形。例如
成为黎曼流形。例如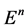 、球面
、球面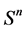 以及一般线性群在适当的黎曼度量下都是黎曼流形。在黎曼流形上要定义一个联络(求导方式)
以及一般线性群在适当的黎曼度量下都是黎曼流形。在黎曼流形上要定义一个联络(求导方式)
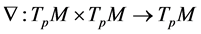
满足线性和莱布尼兹法则。特别地,我们关心特殊的联络——黎曼联络,满足对称性
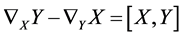
和相容性
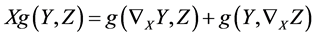
其中
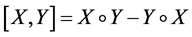
称为Lie括号。有了黎曼我们就可以定义黎曼曲率张量
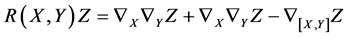
流形的曲率定义为
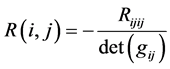
其中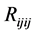 为曲率张量的分量。例如
为曲率张量的分量。例如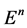 的曲率为零,
的曲率为零,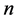 维球面
维球面 的曲率为1。测地线是流形上连接相邻两点距离的最短线,满足
的曲率为1。测地线是流形上连接相邻两点距离的最短线,满足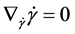 ,其中
,其中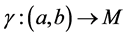 ,用分量表示为
,用分量表示为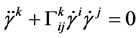 ,其中
,其中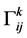 是联络系数。另外,通过变分方法通过求能量泛函的极值同样可以获得测地线方程。对于一般的黎曼流形,其上面的测地线不容易求解,但是对于矩阵流形,我们就可以获得显式的解。通过对能量泛函的二阶变分,我们可以获得沿测地线
是联络系数。另外,通过变分方法通过求能量泛函的极值同样可以获得测地线方程。对于一般的黎曼流形,其上面的测地线不容易求解,但是对于矩阵流形,我们就可以获得显式的解。通过对能量泛函的二阶变分,我们可以获得沿测地线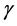 的Jacobi方程
的Jacobi方程
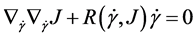
其中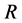 表示曲率张量。利用Jacobi方程我们可以研究Jacobi场的稳定性 [10] [11] [12] 。此外,指数映射和对数映射是联系光滑流形与其切空间的重要数学概念。通过指数映射,我们可以获得流形上过一点和一个切方向的测地线的表达式。
表示曲率张量。利用Jacobi方程我们可以研究Jacobi场的稳定性 [10] [11] [12] 。此外,指数映射和对数映射是联系光滑流形与其切空间的重要数学概念。通过指数映射,我们可以获得流形上过一点和一个切方向的测地线的表达式。
3. 随机信息几何
信息几何不研究单个随机现象,而是把要研究的随机现象全体(概率密度函数)看成一个集合,加上一些条件使之成为一个微分流形,研究该流形的性质以及应用 [1] [2] 。设
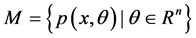
是一个 维统计流形,其中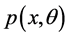 是概率密度函数,
是概率密度函数, 表示参数。作为特例,一元正态分布全体构成的流形
表示参数。作为特例,一元正态分布全体构成的流形
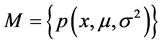
是一个2维流形,其中
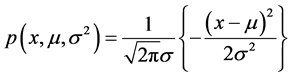
通过引入Fisher信息矩阵
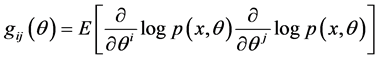
流形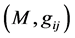 成为一个黎曼流形,其中上式中的
成为一个黎曼流形,其中上式中的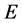 表示数学期望。
表示数学期望。
Amari, S.提出了对偶联络的概念,是对经典联络中关于相容性的推广
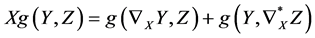
其中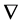 与
与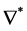 为对偶联络。当联络
为对偶联络。当联络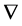 满足对称性以及相容性时,
满足对称性以及相容性时,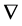 称为黎曼联络。经计算,我们可以计算得到:上述的一元正态分布全体所构成的黎曼流形是一个具有负常曲率的双曲空间。进一步地,Amari, S.定义了特殊的对偶联络
称为黎曼联络。经计算,我们可以计算得到:上述的一元正态分布全体所构成的黎曼流形是一个具有负常曲率的双曲空间。进一步地,Amari, S.定义了特殊的对偶联络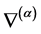 与
与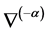

上述定义的好处在于,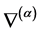 是对称联络而且
是对称联络而且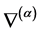 与
与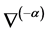 是对偶联络。另外,如所周知,指数分布族
是对偶联络。另外,如所周知,指数分布族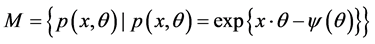
包含了许多重要的分布,其中 表示势函数。通过计算可知,指数分布族流形的几何量由
表示势函数。通过计算可知,指数分布族流形的几何量由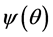 完全确定。不同于标准的距离函数,在随机信息几何中可以利用Kullback-Leibler散度
完全确定。不同于标准的距离函数,在随机信息几何中可以利用Kullback-Leibler散度
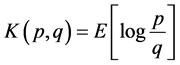
来衡量两个分布的差异,其中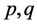 是密度函数。另外,可以引入散度(Divergence)
是密度函数。另外,可以引入散度(Divergence)
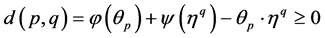
其中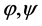 是势函数。该散度只满足非负性,不满足对称性和三角不等式。此外还可以引入Bregman散度等来推广Kullback-Leibler散度。
是势函数。该散度只满足非负性,不满足对称性和三角不等式。此外还可以引入Bregman散度等来推广Kullback-Leibler散度。
自然梯度广泛用于求定义在黎曼流形上的目标函数的最优值,其中的迭代公式与黎曼度量有关。设
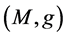 是黎曼流形,
是黎曼流形,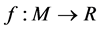 ,通过迭代公式
,通过迭代公式
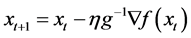
来求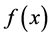 的最小值,其中
的最小值,其中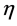 表示迭代步长。
表示迭代步长。
4. 矩阵信息几何的基本内容
李群是以一个流形同时又是一个群 [13] [14] 。抽象的李群是很难去使用的,矩阵李群具有广泛的应用。通过在李群上引入适当的度量,使得李群具有很好的几何性质,以便使用。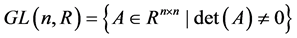 或
或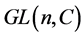 是实数域或复数域上的一般线性群,可以证明,它们是光滑的流形而且在通常矩阵的乘法意义下构成群,从而它们是李群。
是实数域或复数域上的一般线性群,可以证明,它们是光滑的流形而且在通常矩阵的乘法意义下构成群,从而它们是李群。
对于非随机的情形,上面的理论已经不再适用,一般线性群的李子群以及子流形发挥重要的作用。我们关心它们的李子群,例如正交群
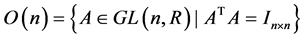
酉群

以及特殊辛群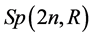 ,它们都是紧致的李群。同时,
,它们都是紧致的李群。同时,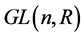 的一些子流形,例如正定矩阵全体构成的流形
的一些子流形,例如正定矩阵全体构成的流形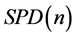 ,特殊欧几里得群
,特殊欧几里得群

Steifel流形
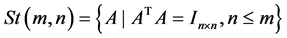
以及Grassmann流形等在信息几何的应用中发挥重要作用。既然对于同一个流形,赋予其不同的度量将具有不同的几何结构,我们需要根据解决问题的需要定义适当的度量。
测地线的理论在信息几何的研究中有重要的作用,局部上它是连接流形上两点的最短线。但是对于抽象的流形,测地线的方程往往满足一个非线性的方程,无法给出解析解。然而,对于矩阵流形,我们可以给出测地线的显式表达。另外,在求解一个定义在一般的黎曼流形上的函数的最小值时,我们需要利用自然梯度给出相应的迭代公式。但是,其中的求逆运算在求解过程中增加了复杂性。在矩阵流形上,根据具体的情形我们可以给出黎曼梯度的简洁表达式,使得运算过程变得相对简单 [12] [13] [14] 。
5. 矩阵流形上的几何度量
在统计流形上我们可以定义Fisher信息矩阵,使之成为黎曼流形,而对于矩阵流形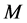 ,我们可以定义不同的黎曼度量,使之成为黎曼流形 [13] [14] [15] [16] [17] 。例如在一般线性群
,我们可以定义不同的黎曼度量,使之成为黎曼流形 [13] [14] [15] [16] [17] 。例如在一般线性群 上定义欧氏度量
上定义欧氏度量
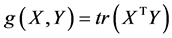
则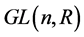 成为一个欧氏空间,其中
成为一个欧氏空间,其中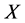 与
与 为
为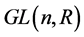 上任意一点处的切空间的元素,该定义与
上任意一点处的切空间的元素,该定义与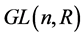 上点的选取无关。另一方面,如果我们定义
上点的选取无关。另一方面,如果我们定义
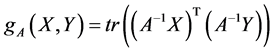
则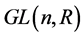 成为一个弯曲的黎曼流形。但是,由于
成为一个弯曲的黎曼流形。但是,由于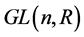 不连通,具有两个连通分支,我们只能在每一个连通分支上给出相应的测地线,以及进行最优化的计算等。
不连通,具有两个连通分支,我们只能在每一个连通分支上给出相应的测地线,以及进行最优化的计算等。
正定矩阵流形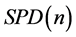 在信息几何的研究中发挥重要的作用,例如多元正态分布的协方差矩阵就是正定矩阵,在核磁共振、雷达信号处理等领域具有广泛的应用。如果我们在
在信息几何的研究中发挥重要的作用,例如多元正态分布的协方差矩阵就是正定矩阵,在核磁共振、雷达信号处理等领域具有广泛的应用。如果我们在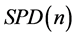 上定义欧氏度量
上定义欧氏度量
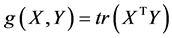
此时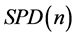 成为一个欧氏空间,其上面连接任意两点
成为一个欧氏空间,其上面连接任意两点 的测地线是一条直线
的测地线是一条直线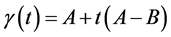 ,从该式子我们发现:该直线不能总是在
,从该式子我们发现:该直线不能总是在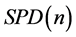 上,这是我们不希望的结果,因为我们经常要在一个流形上衡量连接任意两点的最短距离(测地线的最短距离)。现在我们定义另一个黎曼度量
上,这是我们不希望的结果,因为我们经常要在一个流形上衡量连接任意两点的最短距离(测地线的最短距离)。现在我们定义另一个黎曼度量
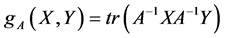
其中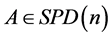 ,
,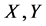 属于
属于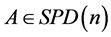 的切空间。于是
的切空间。于是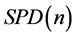 成为一个Hadamad空间(完备的,带有非正曲率的空间)。此时,在
成为一个Hadamad空间(完备的,带有非正曲率的空间)。此时,在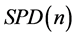 上,任意两点
上,任意两点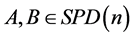 都可以用测地线连接,测地线的方程为
都可以用测地线连接,测地线的方程为
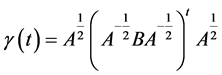
此时连接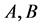 两点的距离(测地距离)定义为
两点的距离(测地距离)定义为
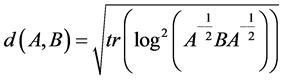
Pennec,Xavier [5] 在等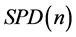 上定义了另一个黎曼度量,通过指数映射给出
上定义了另一个黎曼度量,通过指数映射给出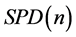 的切空间与其本身的线性等距,使得
的切空间与其本身的线性等距,使得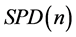 成为一个特殊的欧氏空间,因此在
成为一个特殊的欧氏空间,因此在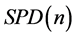 上获得更加简洁的衡量两点间距离的函数。
上获得更加简洁的衡量两点间距离的函数。
在一般线性群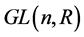 的紧李群上,我们可以定义双不变的黎曼度量
的紧李群上,我们可以定义双不变的黎曼度量
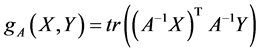
其中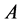 和
和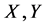 分别是相应的李群以及切空间上的元素。在该黎曼度量意义下,紧李群成为带有非负曲率的黎曼流形,而连通的紧李群是测地完备的,换句话说,连通的紧李群上任意两点都可由测地线来连接。另外,还有一些重要的李群或流形属于一般线性群的李子群或子流形。例如特殊欧几里得群
分别是相应的李群以及切空间上的元素。在该黎曼度量意义下,紧李群成为带有非负曲率的黎曼流形,而连通的紧李群是测地完备的,换句话说,连通的紧李群上任意两点都可由测地线来连接。另外,还有一些重要的李群或流形属于一般线性群的李子群或子流形。例如特殊欧几里得群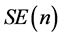 在机器人控制与图像处理等领域具有重要的应用。
在机器人控制与图像处理等领域具有重要的应用。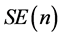 不是紧李群,其上面不存在双不变度量,但是存在左不变度量或右不变度量,由此在
不是紧李群,其上面不存在双不变度量,但是存在左不变度量或右不变度量,由此在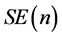 定义上述度量后它成为一个黎曼流形。同时,
定义上述度量后它成为一个黎曼流形。同时, 上的测地线可以显式地给出。Steifel流形是紧致的,正交群和单位球面属于Steifel流形的特例。Steifel流形的几何结构在流形的优化等领域具有重要应用 [18] [19] [20] 。
上的测地线可以显式地给出。Steifel流形是紧致的,正交群和单位球面属于Steifel流形的特例。Steifel流形的几何结构在流形的优化等领域具有重要应用 [18] [19] [20] 。
6. 信息几何与控制理论
本章介绍信息几何理论在控制理论中的应用。首先,研究随机系统的控制 [21] [22] [23] [24] [25] ,然后通过几何算法来求解Lyapunov方程与Riccati方程,研究线性系统的稳定性与最优控制 [26] [27] [28] [29] 。
既然几乎所有的控制系统都受制于随机信号,随机控制系统是常用的系统,如传感器的噪声,系统参数的随机微小变化等都会对控制系统产生随机影响。在造纸工艺中,要求得到的成品纸张的重量及密度都近似地服从正态分布。但当生产线发生异常时,就不再严格服从正态分布。于是就要设计控制, 使得这些质量参数重新服从正态分布。Dodson,Christopher T. J.和Wang,Hong [21] 设计了随机分布控制系统的输出服从Gamma概率密度函数时控制器的两种方法。具体来说就是利用测地线得到对控制器的方法以及利用B-spline函数得到的控制方法。
随机控制问题的核心思想是:要设计一个控制系统,使得系统的输出所满足的概率与事先指定目标越接近越好。随机分布控制也被认为是对概率密度函数形状的控制,其成功地克服了目前最小方差控制仅能研究高斯型随机控制系统的局限。
对于这个问题,我们的主要思想是把输出概率分布全体看成一个统计流形,通过把函目标函数参数化,使之具有概率分布的形式,而且把这样的参数化的目标函数看成流形,把要研究的问题归结成为求两个流形之间的最小距离问题。再引入Kullback-Leibler散度作为距离函数,来求解该问题。进一步,可以考虑带有噪音的情形以及带有反馈的情形。
对于系统的结构未知、系统输出可测的随机分布控制系统, 通过引入B-spline流形, 借助于自然梯度-投影算法和测地-投影算法可给出随机分布控制系统的控制策略。
关于线性系统的稳定性问题,通常可以寻找一个Lyapunov函数,它满足非负性而且其导数是非正的。问题最后归结为对于给定的一个正定矩阵,求解一个Lyapunov方程。例如,对于线性系统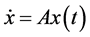 ,设
,设 ,其中
,其中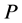 是正定矩阵,可以验证
是正定矩阵,可以验证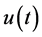 是非负的而且其导数是非正的。要研究该线性系统的稳定性问题归结为对于给定的正定矩阵
是非负的而且其导数是非正的。要研究该线性系统的稳定性问题归结为对于给定的正定矩阵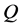 ,方程
,方程
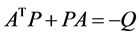
关于正定矩阵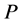 是否有解。我们把
是否有解。我们把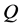 和
和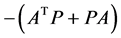 都看成正定矩阵流形
都看成正定矩阵流形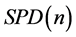 的点,它们由测地线连接。
的点,它们由测地线连接。
我们利用测地距离衡量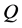 和
和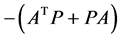 的差异,我们希望连接这两点的测地距离越小越好。可以使用
的差异,我们希望连接这两点的测地距离越小越好。可以使用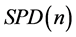 上的自然梯度的迭代方法来求数值解,从而给出稳定性问题的求解。对于Lyapunov方程的求解问题,已经有许多数值解法。我们利用信息几何的方法来求解,获得的算法具有迭代步骤少的特点。
上的自然梯度的迭代方法来求数值解,从而给出稳定性问题的求解。对于Lyapunov方程的求解问题,已经有许多数值解法。我们利用信息几何的方法来求解,获得的算法具有迭代步骤少的特点。
另外,人们经常要面临这样的需求:对于一个线性系统,给定的一个目标函数,寻找系统输入使得目标函数取得最优值。问题最终归结为求解Riccati方程。我们给出了Riccati方程几何求解方法,给出了最优控制的几何算法。具体地,对于线性系统
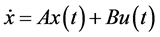
要设计输入 使得指定的目标函数
使得指定的目标函数
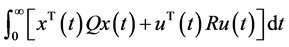
达到最小值,其中 是正定矩阵。该问题可以归结为求解关于正定矩阵的Riccati方程
是正定矩阵。该问题可以归结为求解关于正定矩阵的Riccati方程
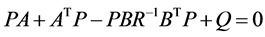
利用上述类似的方法我们可以给出Riccati方程的数值解,从而获得最小值。与其它的方法相比较我们的方法具有迭代次数少的优点。
基金项目
本课题获得国家自然科学基金项目(No. 61179031)的资助。
文章引用
韩希武,孙华飞,张真宁. 信息几何与控制理论
Information Geometry and Control Theory[J]. 动力系统与控制, 2016, 05(04): 135-142. http://dx.doi.org/10.12677/DSC.2016.54015
参考文献 (References)
- 1. Amari, S. (1985) Differential-Geometrical Methods in Statistics. Springer Lectures Notes in Statistics, 28, 11-65. http://dx.doi.org/10.1007/978-1-4612-5056-2_2
- 2. Amari, S. and Nagaoka, H. (2007) Methods of Information Geometry. American Mathematical Soc, Vol. 191.
- 3. Barbaresco, F. (2008) Innovative Tools for Radar Signal Processing Based on Cartan’s Geometry of SPD Matrices & Information Geometry. 2008 IEEE Radar Conference. IEEE. http://dx.doi.org/10.1109/RADAR.2008.4720937
- 4. Barbaresco, F. (2009) Interactions between Symmetric Cone and Infor-mation Geometries: Bruhat-Tits and Siegel Spaces Models for High Resolution Autoregressive Doppler Imagery, Emerging Trends in Visual Computing. Springer, Berlin, Heidelberg.
- 5. Pennec, X., Fillard, P. and Ayache, N. (2006) A Riemannian Framework for Tensor Computing. International Journal of Computer Vision, 66, 41-66. http://dx.doi.org/10.1007/s11263-005-3222-z
- 6. Du, S., Zheng, N., Ying, S. and Liu, J. (2010) Affine Iterative Closest Point Algorithm for Point Set Registration. Pattern Recognition Letters, 31, 791-799. http://dx.doi.org/10.1016/j.patrec.2010.01.020
- 7. Du, S., Zheng, N., Xiong, L., Ying, S. and Xue, J. (2010) Scaling Iterative Closest Point ALGORITHM for Registration of m–D Point Sets. Journal of Visual Communication and Image Representation, 21, 442-452. http://dx.doi.org/10.1016/j.jvcir.2010.02.005
- 8. 黎湘, 程永强, 王宏强, 秦玉亮.雷达信号处理的信息几何[M]. 北京: 科学出版社, 2013.
- 9. 黎湘, 程永强, 王宏强, 秦玉亮. 信息几何理论与应用研究进展[J]. 中国科学, 43(2013): 707-732.
- 10. Peng, L., Sun, H., Sun, D. and Yi, J. (2011) The Geometric Structures and Instability of Entropic Dynamical Models. Advances in Mathematics, 227, 459-471. http://dx.doi.org/10.1016/j.aim.2011.02.002
- 11. Peng, L., Sun, H. and Xu, G. (2012) Information Geometric Characterization of the Complexity of Fractional Brownian Motions. Journal of Mathematical Physics, 53, 123305. http://dx.doi.org/10.1063/1.4770047
- 12. Li, C., Sun, H. and Zhang, S. (2013) Characterization of the Complexity of an ED Model via Information Geometry. The European Physical Journal Plus, 128, 1-6. http://dx.doi.org/10.1140/epjp/i2013-13070-8
- 13. Hall, B.C. (2015) Lie Groups, Lie Algebras, and Representations: An Ele-mentary Introduction (Vol. 222). Springer, New York. http://dx.doi.org/10.1007/978-3-319-13467-3
- 14. 孙华飞, 张真宁, 彭林玉, 段晓敏. 信息几何导引[M]. 北京: 科学出版社, 2016.
- 15. Nielsen, F. and Bhatia, R. (2013) Matrix Information Geometry. Springer, New York. http://dx.doi.org/10.1007/978-3-642-30232-9
- 16. Moakher, M. (2005) A Differential Geometric Approach to the Geometric Mean of Symmetric Positive-Definite Matrices. SIAM Journal on Matrix Analysis and Applications, 26, 735-747. http://dx.doi.org/10.1137/S0895479803436937
- 17. Moakher, M. and Zéraï, M. (2011) The Riemannian Geometry of the Space of Positive-Definite Matrices and Its Application to the Regularization of Positive-Definite Matrix-Valued Data. Journal of Mathe-matical Imaging and Vision, 40, 171-187. http://dx.doi.org/10.1007/s10851-010-0255-x
- 18. Fiori, S. (2011) Solving Mini-mal-Distance Problems over the Manifold of Real-Symplectic Matrices. SIAM Journal on Matrix Analysis and Applications, 32, 938-968. http://dx.doi.org/10.1137/100817115
- 19. Fiori S. (2011) Extended Hamiltonian Learning on Riemannian Manifolds: Theoretical Aspects. IEEE Transactions on Neural Networks, 22, 687-700. http://dx.doi.org/10.1109/TNN.2011.2109395
- 20. Fiori S. (2012) Extended Hamiltonian Learning on Riemannian Manifolds: Numerical Aspects. IEEE Transactions on Neural Networks and Learning Systems, 23, 7-21. http://dx.doi.org/10.1109/TNNLS.2011.2178561
- 21. Dodson, C.T.J. and Wang, H. (2001) Iterative Approximation of Statistical Distributions and Relation to Information Geometry. Statistical Inference for Stochastic Processes, 4, 307-318. http://dx.doi.org/10.1023/A:1012289028897
- 22. Zhang, Z., Sun, H. and Zhong, F. (2009) Natural Gradient-Projection Algo-rithm for Distribution Control. Optimal Control Applications and Methods, 30, 495-504. http://dx.doi.org/10.1002/oca.874
- 23. Zhang Z., Sun, H. and Peng, L. (2013) Natural Gradient Algorithm for Stochastic Dis-tribution Systems with Output Feedback. Differential Geometry and Its Applications, 31, 682-690. http://dx.doi.org/10.1016/j.difgeo.2013.07.004
- 24. Zhang, Z., Sun, H., Peng, L. and Jiu, L. (2014) A Natural Gradient Algorithm for Stochastic Distribution Systems. Entropy, 16, 4338-4352. http://dx.doi.org/10.3390/e16084338
- 25. Zhong, F., Sun, H. and Zhang, Z. (2008) An Information Geometry Algorithm for Distribution Control. Bulletin of the Brazilian Mathematical Society, 39, 1-10. http://dx.doi.org/10.1007/s00574-008-0068-3
- 26. Duan, X., Sun, H. and Zhang, Z. (2014) A Natural Gradient Algorithm for the Solution of Lyapunov Equation Based on the Geodesic Distance. Journal of Computational Mathematics, 32, 93-106. http://dx.doi.org/10.4208/jcm.1310-m4225
- 27. Duan, X., Sun, H., Peng, L. and Zhao, X. (2013) A Natural Gradient Descent Algorithm for the Solution of Discrete Algebraic Lyapunov Equations Based on the Geodesic Distance. Applied Mathematics and Computation, 219, 9899- 9905. http://dx.doi.org/10.1016/j.amc.2013.03.119
- 28. Luo, Z. and Sun, H. (2014) Extended Hamil-tonian Algorithm for the Solution of Discrete Algebraic Lyapunov Equations. Applied Mathematics and Computation, 234, 245-252. http://dx.doi.org/10.1016/j.amc.2014.02.037
- 29. Luo, Z., Sun, H. and Duan, X. (2014) The Extended Hamiltonian Algorithm for the Solution of the Algebraic Riccati Equation. Journal of Applied Mathematics, 2014, Article ID: 693659. http://dx.doi.org/10.1155/2014/693659