Open Journal of Acoustics and Vibration
Vol.04 No.03(2016), Article ID:18980,8
pages
10.12677/OJAV.2016.43003
Measuring Effective Parameters of Composite Acoustic Metamaterials Using Impedance Tube
Fangyi Xia1, Zhihong Hang2
1College of Physics, Optoelectronics and Energy, Soochow University, Suzhou Jiangsu
2Collaborative Innovation Center of Suzhou Nano Science and Technology, Suzhou Jiangsu

Received: Oct. 26th, 2016; accepted: Nov. 15th, 2016; published: Nov. 18th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
A new experimental method is developed to precisely measure the effective density and bulk modulus using impedance tube. Considering the multiple reflections on multi-surfaces, a new algorithm using transfer matrix method is considered to obtain the transmission and reflection coefficient through a lossless sample and the corresponding effective parameter can thus be retrieved. Good consistence can be found between simulations and experiments. Having little impact from the absorbing property of the termination, our newly developed method has advantages to traditional impedance tube methods and can benefit the development of acoustic metamaterials.
Keywords:Multiple Reflections, Transfer Matrix, Acoustic Metamaterial

利用阻抗管测量复合声学超材料特性
夏方弈1,杭志宏2
1苏州大学,物理与光电·能源学部,江苏 苏州
2苏州纳米科技协同创新中心,江苏 苏州

收稿日期:2016年10月26日;录用日期:2016年11月15日;发布日期:2016年11月18日

摘 要
本文在考虑了阻抗管中存在多重反射的情况下,利用传递函数法优化得出了样品的透射系数和反射系数,从而获得声学超材料有效材料参数。在比较了不同阻抗管算法实验结果之后,可以发现本文提出的新测量方法和仿真结果有着很好的吻合,可以非常准确的获得材料的有效参量。新发展的测量方法,对消声端的消声吸声要求不高,可以测量不吸声的材料,扩展了阻抗管测量的适用范围,对声学超材料的设计和相关应用都有着一定价值。
关键词 :多重反射,传递矩阵,声学超材料

1. 引言
近年来,人们对声环境的要求愈来愈高。利用结构设计,来构建复合声学材料从而实现对声波更好的操控对声学研究和生活应用也愈来愈重要。声子晶体和声学超材料 [1] 的提出在隔声、防震、热控制等方面有着巨大的研究前景。声子晶体主要以布拉格散射机制实现对波的调控,因此声子晶体的结构尺度都与工作波长相当。而声学超材料是人工结构材料,其结构尺寸远小于其工作波长。因为这一特点,使在超材料中传播的波不能分辨其结构,所以超材料可视为是均匀的有效介质,可用有效参数描述,比如有效质量密度,有效体模量 [2] 。人工共振单元设计可以使声学超材料的有效声学参数是单负、双负的 [3] 。很多以前很难想象的声学应用,比如声隐身 [4] [5] [6] 都可以通过人工设计控制有效密度和有效体模量来实现。虽然人工共振单元帮助实现了很多新奇有趣的声学传播特性 [7] ,但共振结构的窄频宽性质也限制了其应用前景 [8] 。通过将两种具有不同声学特性的材料混合构建的复合声学超材料,可以在一个比较宽的频率范围设计所需的声学特性,是构建宽频声学超材料的基础。声学超材料的设计离不开对材料有效质量密度和有效体模量的测量。发展准确测量声学超材料有效参量的手段对于声学超材料的发展至关重要。
阻抗管是一种用来测量吸声材料的垂直入射吸声系数的装置。其主体是一个具有刚性壁的矩形或者圆形截面的管子。声源在管内产生一个平面波,在样品前方会形成反射,而在样品后会形成透射 [9] 。传统阻抗管利用“三传声器法”进行测量。由于样品表面的反射,入射波和反射波部形成驻波场,需要利用两支传声器把入射波和反射波分开。在透射部分,在阻抗管末端由于安放了理论上没有反射的尖劈状消声端,可以仅利用第三支传声器测量透射波。通过测量声波的透反射可以得到待测材料的声阻抗、隔声量等材料特性。传统阻抗管的测量的准确程度与安放在阻抗管末端的尖劈消声端直接有关 [10] 。改良了的“四传声器法”通过更换不同消声端在一定程度上可以减弱消声端的影响。另外,传统阻抗管算法只考虑待测样品对声波的单次反射且样品通常为吸声材料。这些条件使得传统阻抗管并不适用于通常对声波无吸收的声学超材料的测量。
本文在考虑了阻抗管内存在样品、消声端和声源端等端面多重反射情况下,运用传递函数的方法进行理论推导,完善了“三传声器法”阻抗管的测量算法,可以精确对复合声学超材料声学特性进行测量。
2. 多重反射情况下样品参数的测量
我们首先利用传递函数法推导在存在多重反射的情况下如何求得样品的透/反射系数。图1是我们的

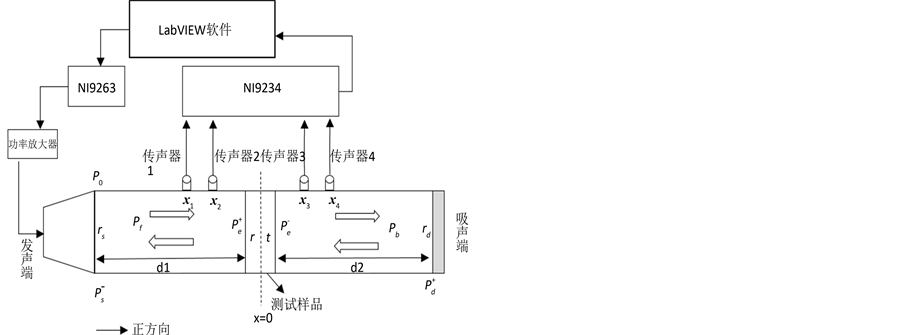 (a) (b)
(a) (b)
Figure 1. Schematic of impedance tube measurement: (a) impedance tube measurement schematic diagram, (b) the impedance tube device
图1. 阻抗管测量及装置示意图:(a) 阻抗管测量示意图,(b) 阻抗管装置图
装置示意图。
如图1所示,以测试样品中点为坐标原点(x = 0),向右为正方向。在样品前和样品后的管子中位于坐标x处的总声场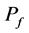 ,
,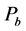 分别为:
分别为:
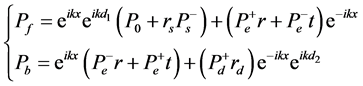 (1)
(1)
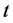 指待求的样品透射系数,待测样品厚度也包括在透射系数中,这也是公式中没有样品厚度(以
指待求的样品透射系数,待测样品厚度也包括在透射系数中,这也是公式中没有样品厚度(以 表示)表达式的原因。
表示)表达式的原因。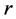 指样品的反射系数,
指样品的反射系数, 指波矢,
指波矢,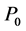 指声源发出的初始声压,
指声源发出的初始声压, 指发声端表面声压,其中“−”表示发声端表面受到声压沿负方向传播。
指发声端表面声压,其中“−”表示发声端表面受到声压沿负方向传播。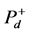 指消声端表面声压,其中“+”表示消声端表面受到声压沿正方向传播。
指消声端表面声压,其中“+”表示消声端表面受到声压沿正方向传播。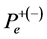 指样品前(后)表面声压,其中“+”(“−”)表示受到声压沿正(负)方向传播。
指样品前(后)表面声压,其中“+”(“−”)表示受到声压沿正(负)方向传播。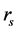 指发声端表面反射系数,
指发声端表面反射系数,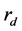 指消声端表面发射系数,
指消声端表面发射系数,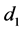 指声源到样品前表面的距离,
指声源到样品前表面的距离,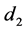 指样品后表面到消声端的距离。每个表面声压分别为:
指样品后表面到消声端的距离。每个表面声压分别为:
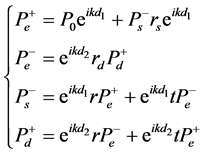 (2)
(2)
解方程(2)可得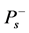 ,
, ,
,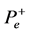 ,
,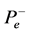 并代入方程(1)得到:
并代入方程(1)得到:
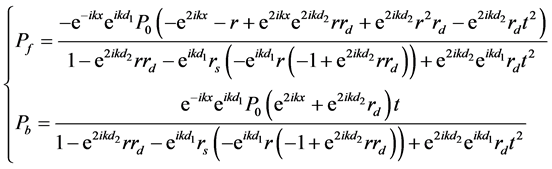 (3)
(3)
通过三支坐标分别为 、
、 、
、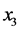 的传声器测得的声压为
的传声器测得的声压为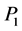 、
、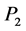 、
、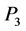 ,将
,将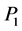 与
与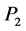 代入
代入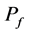 ,
,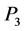 代入
代入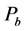 得到方程:
得到方程:
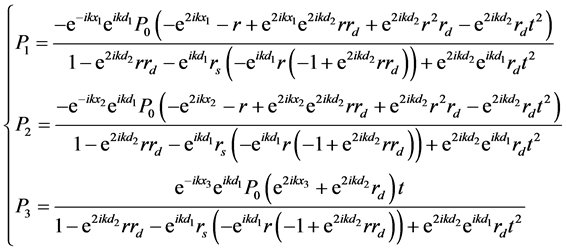 (4)
(4)
联立解方程(4)可以得到透/反射系数。
根据公式(4)只需三支传声器就可以得出待测样品透/反射系数,图1所画出的第四支传声器是为了下文提到的“四传声器法”作对比。在考虑多重反射的情况下,看似公式中存在很多参数,包括初始声压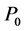 ,发声端表面反射系数
,发声端表面反射系数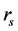 和消声端表面发射系数
和消声端表面发射系数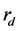 ,并需要确定三支麦克风的位置
,并需要确定三支麦克风的位置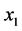 、
、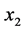 、
、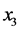 以及样品到发声端以及消声端的距离
以及样品到发声端以及消声端的距离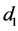 和
和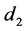 。但在求解过程中,
。但在求解过程中,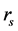 与
与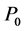 一起被消掉。
一起被消掉。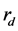 可以通过对不放样品的空场进行测量得出。利用相同方法根据两支传声器测出声压
可以通过对不放样品的空场进行测量得出。利用相同方法根据两支传声器测出声压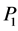 、
、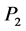 以及两支传声器的坐标
以及两支传声器的坐标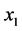 、
、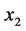 可以得出
可以得出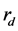 :
:
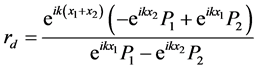 (5)
(5)
在实验测量中,先通过空场测出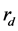 ,再放入待测样品测量,得到其透/反射系数。
,再放入待测样品测量,得到其透/反射系数。
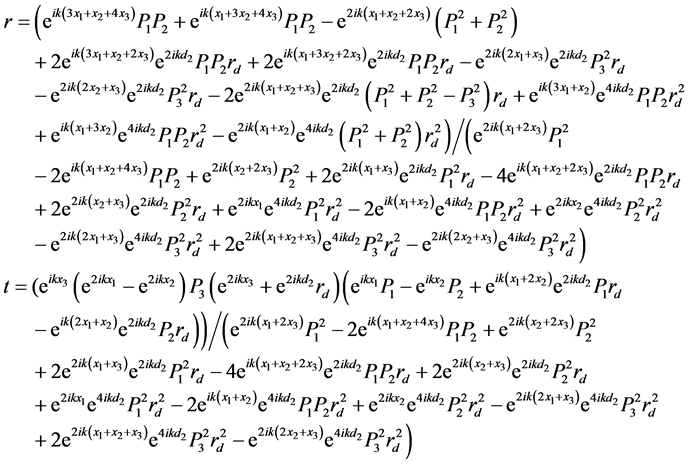 (6)
(6)
实验需要测量样品有效密度和有效体模量。由透/反射系数可以推导出折射率和阻抗比(以空气阻抗为参考) [11] 。
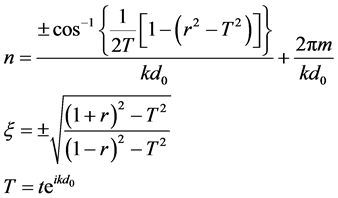 (7)
(7)
公式(7)中,T指透射系数,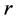 指反射系数。m指整数,是为了让余弦函数数值在−1到1之间,
指反射系数。m指整数,是为了让余弦函数数值在−1到1之间,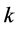 指波矢,
指波矢,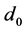 指样品厚度,
指样品厚度,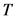 与
与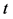 存在样品厚度的相位差。
存在样品厚度的相位差。
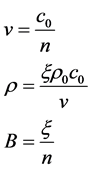 (8)
(8)
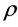 指样品有效密度,
指样品有效密度, 指样品有效体模量,
指样品有效体模量,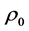 指空气密度,
指空气密度,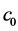 指空气声速,
指空气声速,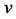 指样品声速。
指样品声速。
3. 实验系统及测量结果
3.1. 阻抗管的测量系统
本文实验中,选用管道壁厚度为0.01 m,内径为0.03 m的圆管阻抗管,基本满足声波沿管道传播无损耗的要求。测量频率上限大约是6300 Hz,频率下限大约是800 Hz。在管道末端选用吸声材料作为消声端,一般选用吸声棉。实验中坐标为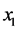 和
和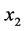 位置的两支传声器间距为0.0225 m,坐标为
位置的两支传声器间距为0.0225 m,坐标为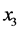 和
和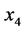 位置的两支传声器间距为0.0225 m。坐标为
位置的两支传声器间距为0.0225 m。坐标为 的传声器距离样品左侧表面距离为0.015 m,坐标为
的传声器距离样品左侧表面距离为0.015 m,坐标为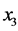 的传声器距离样品右侧表面距离为0.1 m。测量时,第一步把待测样品放置在传声器2和传声器3之间。考虑到样品塞进阻抗管中会产生缝隙造成实验误差,可以考虑把样品做大并采用前管与后管夹住样品的方式进行样品安装与固定。第二步通过LabVIEW控制系统发出单频声音信号。第三步通过传声器接受信号,并对信号进行处理。第四步通过传声器收到信号计算出待测样品透射系数和反射系数。第五步通过透射系数和反射系数得出待测样品有效密度和有效体模量等参数。
的传声器距离样品右侧表面距离为0.1 m。测量时,第一步把待测样品放置在传声器2和传声器3之间。考虑到样品塞进阻抗管中会产生缝隙造成实验误差,可以考虑把样品做大并采用前管与后管夹住样品的方式进行样品安装与固定。第二步通过LabVIEW控制系统发出单频声音信号。第三步通过传声器接受信号,并对信号进行处理。第四步通过传声器收到信号计算出待测样品透射系数和反射系数。第五步通过透射系数和反射系数得出待测样品有效密度和有效体模量等参数。
3.2. 信号的发生和采集
如图1所示,信号的发生装置主要用来提供单频信号,由NI9263模拟输出板卡、功率放大器和扬声器组成。信号采集由传声器,前置放大器和NI9234声振信号采集卡组成。利用LabVIEW软件编写单频信号产生和信号采集程序,通过插接通用计算机的NI9263模拟输出板卡控制信号发生,通过插接通用计算机的NI9234声振信号采集卡控制信号采集。传声器安装时与管壁平齐,确保管内声场不受扰动 [12] 。考虑到传声器的不同,我们通过在同一位置测量进行校准。实验中所用传声器尺寸是1/4英寸,型号是BSWA MPA416。测量分析部分通过推导出的测量公式,对测量得出的声压信号完成传递函数实时计算。
3.3. 实验测量结果
实验中消声端为平头消声端,消声端反射率随频率增大在0.05和0.18之间变化,消声端需要平整测量准确,后文有消声端改变的影响。
本文中通过有机玻璃打孔设计构建了复合声学材料,通过调整占空比可以控制有效密度和体模量 [13] ,这种复合声学材料本身具有各向异性。本文设计的样品厚度是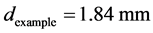 ,直径是
,直径是 ,在玻璃板上打孔使样品与空气阻抗接近匹配。孔的直径是
,在玻璃板上打孔使样品与空气阻抗接近匹配。孔的直径是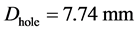 ,占空比是0.465948。有机玻璃密度为1200 kg/m3,有机玻璃声速为2692 m/s,空气密度为1.29 kg/m3,空气声速为345.1405 m/s。
,占空比是0.465948。有机玻璃密度为1200 kg/m3,有机玻璃声速为2692 m/s,空气密度为1.29 kg/m3,空气声速为345.1405 m/s。
为了验证公式推导的正确性,首先利用COMSOL软件对阻抗管模型进行理论仿真,得出理想情况下的样品透射、反射系数,并反推出理想情况下样品的密度。最后用实验进行论证测量,将测试结果与仿真结果做了对比。如图2所示。
图2中用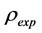 指实验反推出有效密度的实部,图中用直线表示;
指实验反推出有效密度的实部,图中用直线表示; 指实验反推出有效体模量的实
指实验反推出有效体模量的实
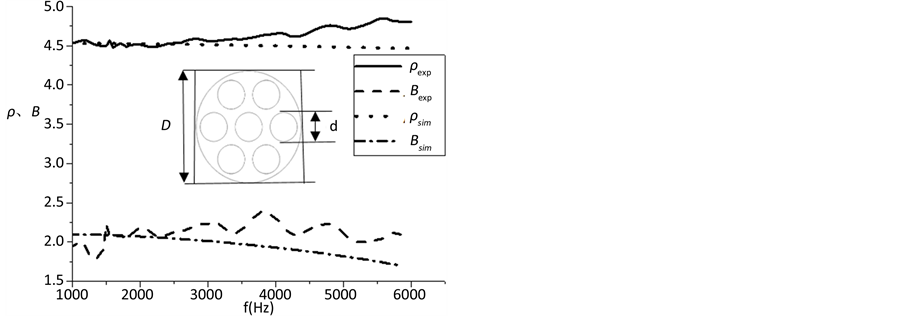
Figure 2. Effective density and bulk modulus obtained by experiments (dashed line) and simulations (solid line) and the schematic of sample is shown in inset
图2. 实验反推样品有效密度和有效体模量与仿真对比及样品示意图
部,图中用短线表示;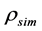 指仿真反推出有效密度的实部,图中用点表示;
指仿真反推出有效密度的实部,图中用点表示;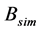 指仿真反推出有效体模量的实部,图中用短线和点的结合表示。在此实验中,选用的平头消声端的反射系数
指仿真反推出有效体模量的实部,图中用短线和点的结合表示。在此实验中,选用的平头消声端的反射系数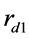 在0.18到0.03之间,数值随频率变化而变化。实验反推样品有效密度的虚部都接近0。从图2可以看出实验反推材料密度和体模量与仿真情况很接近。
在0.18到0.03之间,数值随频率变化而变化。实验反推样品有效密度的虚部都接近0。从图2可以看出实验反推材料密度和体模量与仿真情况很接近。
4. 结果讨论
本文采用完善后的“三传声器法”考虑了阻抗管中样品与发声端和消声端之间存在的多重反射。考虑到本文所用传递函数的方法,实验中应使用平头消声端。图3是本文为了检测重复性做的实验,本文先选用另一根平头消声端(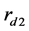 在0.2到0.05之间,数值随频率变化而变化)重复一次实验。为了显示我们实验方法的正确性,我们尝试使用硬墙作为消声端(
在0.2到0.05之间,数值随频率变化而变化)重复一次实验。为了显示我们实验方法的正确性,我们尝试使用硬墙作为消声端(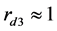 )。实验的结果如图3所示。
)。实验的结果如图3所示。
如图3所示, 指仿真反推样品有效密度实部,图中用直线表示;
指仿真反推样品有效密度实部,图中用直线表示;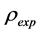 指实验反推出有效密度的实部,图中用短线和点的结合表示;
指实验反推出有效密度的实部,图中用短线和点的结合表示;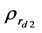 指选取另一个平头消声端反推样品有效密度实部,图中用短线
指选取另一个平头消声端反推样品有效密度实部,图中用短线
表示;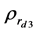 指选用硬墙作为消声端反推样品有效密度实部,图中用点表示。实验反推样品有效密度虚部
指选用硬墙作为消声端反推样品有效密度实部,图中用点表示。实验反推样品有效密度虚部
和有效体模量虚部都接近0。从图中可以看出,选取另外一根消声端也能得出很精确的有效密度实部。有效体模量的吻合程度和很好。即使选取没有吸收的硬墙作为消声端,除了在特定频率由于阻抗管长形成驻波的影响与仿真结果也基本吻合。硬墙作为消声端,会在有些频率让某个传声器的接收到的声场接 近于零,但在大部分频率还是比较接近仿真结果。说明完善后的“三传声器法”对消声端吸声效果要求不高,并且重复性很好。
我们考虑多重反射的“三传声器法”除了对消声端的要求比较简单,对于待测样品的吸声特性也不做要求。而声学超材料的应用中,往往正是需要设计无耗散的材料。尽管“四传声器法”在传统“三消声器法”的基础上,通过在样品与消声端之间增加第四支传声器分开了透射波和消声端的反射波,但由于忽略了多重反射的情况,通常只能准确测量有吸收的材料,并且消声端应使用吸声效果好的尖劈状消声端。如果假设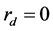 的情况下,公式(6)也可以简化到传统“三传声器法”。图4比较了假设
的情况下,公式(6)也可以简化到传统“三传声器法”。图4比较了假设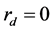 (实际
(实际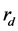 在0.18到0.03之间的情况下)利用传统“三传声器法”,选用反射系数在0.02的尖劈状消声端的“四传声器法”和仿真结果:
在0.18到0.03之间的情况下)利用传统“三传声器法”,选用反射系数在0.02的尖劈状消声端的“四传声器法”和仿真结果:
图4中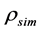 指仿真反推样品有效密度实部,图中用红色直线表示;
指仿真反推样品有效密度实部,图中用红色直线表示;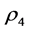 指“四传声器法”反推样品有
指“四传声器法”反推样品有
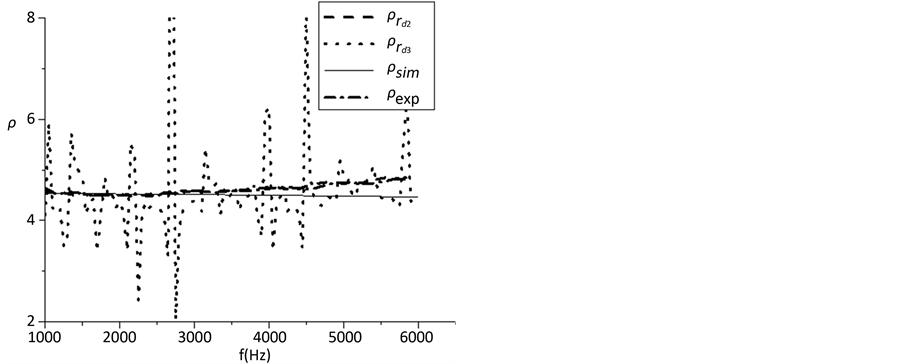
Figure 3. Comparison of effective density between different terminations
图3. 不同消声端反推样品有效密度

Figure 4. Comparison between different experimental methods
图4. 不同实验测量方法反推样品有效密度和有效体模量与仿真对比图
效密度实部,图中用红色短线表示;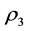 指传统“三传声器法”反推样品有效密度实部,图中用红色点线表示;
指传统“三传声器法”反推样品有效密度实部,图中用红色点线表示;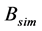 指仿真反推样品有效体模量实部,图中用绿色直线表示;
指仿真反推样品有效体模量实部,图中用绿色直线表示; 指“四传声器法”反推样品有效体模量实部,图中用绿色短线表示;
指“四传声器法”反推样品有效体模量实部,图中用绿色短线表示; 指传统“三传声器法”反推样品有效体模量实部,图中用绿色点线表示。从图4可以看出,“四传声器法”实验反推样品有效密度和有效体模量确实比传统“三传声器法”更接近仿真值,但是不如完善后的“三传声器法”精确。
指传统“三传声器法”反推样品有效体模量实部,图中用绿色点线表示。从图4可以看出,“四传声器法”实验反推样品有效密度和有效体模量确实比传统“三传声器法”更接近仿真值,但是不如完善后的“三传声器法”精确。
5. 结论
本文考虑阻抗管中存在多重反射情况推导出了更接近实际的理论公式。实验结果相比于传统“三传声器法”和“四传声器法”更接近仿真结果。传统“三传声器法”和“四传声器法”一般用来测试吸声材料隔声量和声阻抗。需要吸声效果非常好的消声端,所以一般都用吸声海绵做成尖劈状消声端。而对于而本文的方法考虑了多重反射情况,应用样品范围比较广,不仅适用于吸声样品也适用于无吸声样品。并且对于消声端的吸声效果要求并不高,只要求消声端是平头就可以,甚至硬墙都可以测出比较准确的结果。而这些特点是传统“三传声器法”和“四传声器法”很难做到的。换掉消声端重复实验,结果相同说明方法具有普遍性,重复性。
文章引用
夏方弈,杭志宏. 利用阻抗管测量复合声学超材料特性
Measuring Effective Parameters of Composite Acoustic Metamaterials Using Impedance Tube[J]. 声学与振动, 2016, 04(03): 19-26. http://dx.doi.org/10.12677/OJAV.2016.43003
参考文献 (References)
- 1. Liu, Z.Y., Zhang, X.X., Mao, Y.W., Zhu, Y.Y., Yang, Z.Y., Chan, C.T. and Sheng, P. (2000) Locally Resonant Sonic Materials. Science, 289, 1734-1736. https:/doi.org/10.1126/science.289.5485.1734
- 2. Zigoneanu, L., Popa, B.-I., Starr, A.F. and Cummer, S.A. (2011) Design and Measurements of a Broadband Two- Dimensional Acoustic Metamaterial with Anisotropic Effective Mass Density. Journal of Applied Physics, 109, Article ID: 054906. https:/doi.org/10.1063/1.3552990
- 3. Yang, M., Ma, G., Yang, Z. and Sheng, P. (2013) Coupled Membranes with Doubly Negative Mass Density and Bulk Modulus. Physical Review Letters, 110, 134301. https:/doi.org/10.1103/PhysRevLett.110.134301
- 4. Hu, W.L., Fan, Y.X., Ji, P.F. and Yang, J. (2013) An Experimental Acoustic Cloak for Generating Virtual Images. Journal of Applied Physics, 113, Article ID: 024911. https:/doi.org/10.1063/1.4775408
- 5. Popa, B.-I., Zigoneanu, L. and Cummer, S.A. (2011) Experimental Acoustic Ground Cloak in Air. Physical Review Letters, 106, Article ID: 253901. https:/doi.org/10.1103/PhysRevLett.106.253901
- 6. 赖耘, 杭志宏, 黄学勤, 陈子亭. 隐身材料[J]. 中国物理学会, 中国科学院物理研究所, 2012(9): 589-594.
- 7. Zhai, S.L., Chen, H.J., Ding, C.L. and Zhao, X.P. (2013) Double-Negative Acoustic Metamaterial Based on Meta- Molecule. Journal of Physics D: Applied Physics, 46, Article ID: 475105. https:/doi.org/10.1088/0022-3727/46/47/475105
- 8. Ma, G.C., Yang, M., Xiao, S.W., Yang, Z.Y. and Sheng, P. (2014) Acoustic Metasurface with Hybrid Resonances. Nature Materials, 13, 873-878. https:/doi.org/10.1038/nmat3994
- 9. 袁健, 贺才春, 林胜. 阻抗管中的隔声量测试方法[J]. 中国声学学会, 2006(4): 108-110.
- 10. 朱蓓丽, 罗晓辉. 驻波管的隔声量测试方法[J]. 中国声学学会, 2000(6): 41-43.
- 11. Fokin, V., Ambati, M., Sun, C. and Zhang, X. (2007) Method for Retrieving Effective Properties of Locally Resonant Acoustic Metamaterials. Physical Review B, 76, Article ID: 144302. https:/doi.org/10.1103/PhysRevB.76.144302
- 12. 冯涛, 刘斌, 王晶, 吴雪, 张力. 基于LabVIEW的材料法向吸声系数测量实验系统的研制[J]. 北京长城航空测控技术研究所, 2010, 29(10): 32-37.
- 13. Popa, B.-I. and Cummer, S.A. (2009) Design and Characterization of Broadband Acoustic Composite Metamaterials. Physical Review B, 80, Article ID: 174303. https:/doi.org/10.1103/PhysRevB.80.174303