Open Journal of Nature Science
Vol.04 No.02(2016), Article ID:17353,7
pages
10.12677/OJNS.2016.42012
Stability of an Eco-Epidemiological System with Delay
Tianrong Gong, Weirui Zhao
Wuhan University of Technology, Wuhan Hubei

Received: Mar. 29th, 2016; accepted: Apr. 11th, 2016; published: Apr. 14th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, a delayed eco-epidemiological system with a disease in prey is considered. Its dynamics of stability and the effect of delay on this system have been studied. The system without delay is locally asymptotically stable at the internal equilibrium point. With the delay gradually increasing, the system will be unstable and occurHopf bifurcation. Finally, the numerical simulation is carried out to verify the conclusions. These results can predict the trend of the populations with disease, and provide a reliable theoretical basis for controlling the spread of disease in populations.
Keywords:Delay, Stability, Hopf Bifurcation, Eco-Epidemiological System

具有时滞的生态传染病系统的稳定性分析
龚天蓉,赵维锐
武汉理工大学,湖北 武汉

收稿日期:2016年3月29日;录用日期:2016年4月11日;发布日期:2016年4月14日

摘 要
本文考虑了疾病在食饵种群中传播和具有Holling II型功能反应的时滞生态系统,主要分析时滞对系统局部稳定性的影响。当时滞不存在时,系统在内部平衡点处是局部渐近稳定的;但随着时滞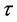 的逐渐增加并超过临界值时,系统由稳定状态变为不稳定且产生Hopf分支,从而得到了Hopf分支的存在条件,最后利用数值模拟来验证所得结论。这些结论预测了疾病在种群间的发展趋势,并为控制疾病在种群间传播提供了可靠的理论依据。
的逐渐增加并超过临界值时,系统由稳定状态变为不稳定且产生Hopf分支,从而得到了Hopf分支的存在条件,最后利用数值模拟来验证所得结论。这些结论预测了疾病在种群间的发展趋势,并为控制疾病在种群间传播提供了可靠的理论依据。
关键词 :时滞,稳定性,Hopf分支,生态传染病系统

1. 引言
生态传染病模型作为种群生态学与传染病动力学的结合学科,主要研究疾病在相互作用的种群之间的传播,其重要的生态学意义已经得到了许多学者的注意。食饵–捕食者系统是描述种群动力学的一类非常重要的模型 [1] - [9] ,其带有功能反应函数的系统能更确切地描述实际的生态捕食情况。当疾病在种群中流行时,如果不加以科学有效的控制,会导致种群的灭绝,所以为更有效的控制疾病并保护物种的多样性,对生态传染病模型的深入研究则起到了举足轻重的作用 [9] 。2013年,Sasmal等人在文献 [1] 中提出食饵染病的非线性食饵捕食者模型:
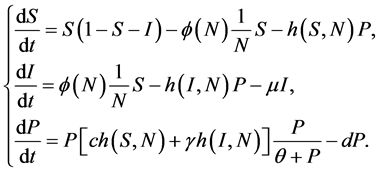 (1)
(1)
其中 和
和 分别表示易感食饵、染病食饵和捕食者的种群数量,
分别表示易感食饵、染病食饵和捕食者的种群数量, 表示所有的食饵数量,
表示所有的食饵数量,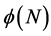 是疾病的传播函数,
是疾病的传播函数,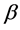 是疾病的传染率。
是疾病的传染率。 和
和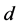 分别是染病食饵的死亡率和捕食者的自然死亡率。我们假设捕食者分别以
分别是染病食饵的死亡率和捕食者的自然死亡率。我们假设捕食者分别以 ,
, 的速率捕食易感食饵和染病食饵,
的速率捕食易感食饵和染病食饵,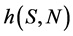 ,
,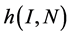 可取Holling I,Holling II或者Holling III这三种形式的功能反应函数。2015年,Santanu Biswas, Sourav Kumar Sasmal等人在文献 [2] 中改进了上述的食饵捕食者模型,
可取Holling I,Holling II或者Holling III这三种形式的功能反应函数。2015年,Santanu Biswas, Sourav Kumar Sasmal等人在文献 [2] 中改进了上述的食饵捕食者模型,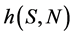 ,
,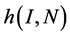 可都取Holling I型功能反应函数,分析了系统的三个边界平衡点和一个内部平衡点的局部稳定性,以及正平衡点处的持久性和系统的全局稳定性。
可都取Holling I型功能反应函数,分析了系统的三个边界平衡点和一个内部平衡点的局部稳定性,以及正平衡点处的持久性和系统的全局稳定性。
功能反应函数在种群动力学中已经得到了广泛的应用,它表示的是单位时间内每个捕食者对食饵的捕食能力,其依赖的因素有很多,例如:食饵的种群密度、捕食者对食饵的搜索和捕食率等。在通过不断地实验研究后,人们提出了针对不同物种的Holling I、Holling II和Holling III型的且具有单调性的功能反应函数。
本文将考虑具有Holling II型功能反应函数的食饵染病的食饵捕食者模型,假设捕食者仅捕食染病食饵,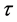 为捕食者的妊娠时滞,此时系统为:
为捕食者的妊娠时滞,此时系统为:
 (2)
(2)
所有参数除了 都是非负的。当
都是非负的。当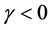 时,捕食染病食饵会增加捕食者的死亡率。
时,捕食染病食饵会增加捕食者的死亡率。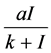 是Holling II型功能反应函数,
是Holling II型功能反应函数, 为捕食者的攻击率,
为捕食者的攻击率,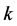 是捕食者种群的半饱和参数,
是捕食者种群的半饱和参数, 为疾病的传染率。我们可选取系统的初始值条件为:
为疾病的传染率。我们可选取系统的初始值条件为:

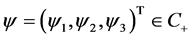 ,对于
,对于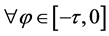 都有
都有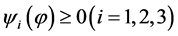 ,
,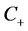 表示连续函数的Banach空间
表示连续函数的Banach空间 。
。
本文的组织安排如下:第2部分主要分析了内部平衡点的稳定性,第3部分利用Matlab进行了相应的数值模拟来说明所得的结论。最后,在第4部分讨论和总结了相关结论。
2. 平衡点的稳定性
系统(2)存在三个边界平衡点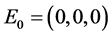 ,
, ,
,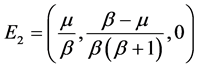 。若条件
。若条件 成立,则存在唯一正平衡点
成立,则存在唯一正平衡点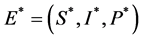 ,其中
,其中
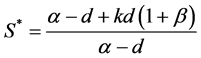 ,
, ,
,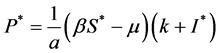 。
。
对于平衡点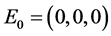 ,特征方程为:
,特征方程为:
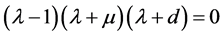 ,
,
显然有一个正根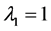 ,则
,则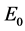 始终不稳定,所以种群是不会灭绝的。
始终不稳定,所以种群是不会灭绝的。
利用特征方程的方法 [10] 来说明内部平衡点 的局部稳定性,系统(2)在
的局部稳定性,系统(2)在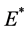 处的线性化方程为
处的线性化方程为
 (3)
(3)
则平衡点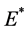 处的特征方程为
处的特征方程为
 (4)
(4)
其中
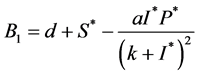 ,
,
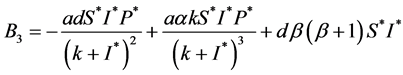 ,
, ,
,
 ,
,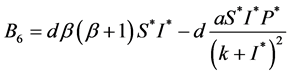 。
。
当 时,方程(4)可化为
时,方程(4)可化为
 (5)
(5)
根据Hurwitz判定定理,当
 (6)
(6)
成立时,方程的所有根均具有负实部,此时系统在平衡点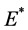 处渐进稳定。
处渐进稳定。
当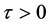 时,假设
时,假设 是方程(4)的解,代入方程并分离实部和虚部有
是方程(4)的解,代入方程并分离实部和虚部有
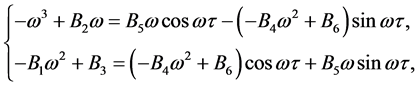 (7)
(7)
将(7)式两端平方相加得
 (8)
(8)
其中 ,
, ,
, ,令
,令 ,则(8)式变为
,则(8)式变为
 (9)
(9)
引理1对于方程(8)有:
(1) 若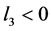 ,则方程(9)至少有一个正根;
,则方程(9)至少有一个正根;
(2) 若 且
且 ,则方程不存在正根;
,则方程不存在正根;
(3) 若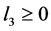 ,
,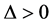 ,
,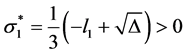 且
且 ,则方程有正根。
,则方程有正根。
假设方程(9)有正根,不失一般性,设其有3个正根,分别记为,那么方程(9)有3个正实根,分别为 ,
,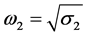 ,
, 。由(7)式可得
。由(7)式可得
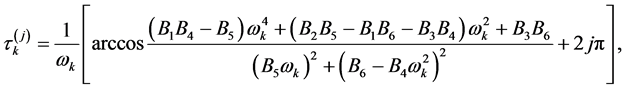
其中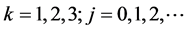 ,因此,
,因此,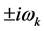 是方程(4)在
是方程(4)在 处的一对纯虚根。记
处的一对纯虚根。记 ,
, 为方程(4)在
为方程(4)在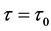 处满足
处满足 的根。将
的根。将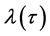 代入方程(4)并对
代入方程(4)并对 求导可得:
求导可得:
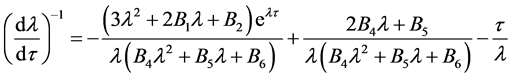
所以有:

当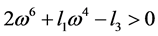 时,
时,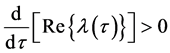 ,系统在
,系统在 处产生Hopf分支。
处产生Hopf分支。
定理1对于系统(2)和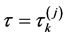 与
与 ,有:
,有:
(1) 若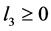 且
且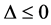 时,平衡点
时,平衡点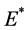 对所有
对所有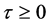 都是渐进稳定的;
都是渐进稳定的;
(2) 若 或
或 ,
, ,
, ,
, ,则对
,则对 ,
, 是渐进稳定的;
是渐进稳定的;
(3) 若条件(2)成立,同时有 ,当
,当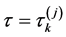 时,系统在
时,系统在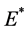 处产生Hopf分支。
处产生Hopf分支。
3. 数值模拟
下面利用Matlab来验证上面所得的结论,选取参数 ,
, ,
,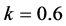 ,
,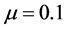 ,
,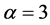 ,
, ,系统的初始条件为
,系统的初始条件为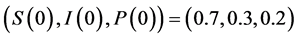 ,则此时系统有唯一内部平衡点
,则此时系统有唯一内部平衡点 。
。
当选取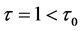 时,系统是渐进稳定的,三者会处于一个长期平稳的发展阶段,疾病的传播得到了控制,如图1和图2所示。而随着
时,系统是渐进稳定的,三者会处于一个长期平稳的发展阶段,疾病的传播得到了控制,如图1和图2所示。而随着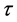 逐渐增加且超过临界值,当
逐渐增加且超过临界值,当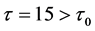 时,系统会在
时,系统会在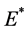 处失去稳定性,且在此时产生Hopf分支,产生的周期解如图3和图4所示,此时疾病并不会得到控制,会周期性的影响食饵种群和捕食者种群的数量。
处失去稳定性,且在此时产生Hopf分支,产生的周期解如图3和图4所示,此时疾病并不会得到控制,会周期性的影响食饵种群和捕食者种群的数量。

Figure 1. τ0 = 1, the phase diagram of the system
图1. 当τ0 = 1时,系统的相图
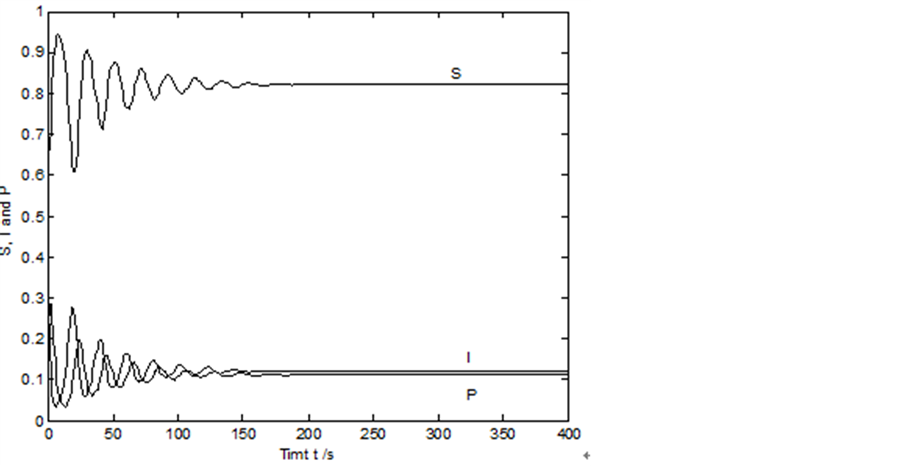
Figure 2. τ0 = 1, the plan graph of the system
图2. 当τ0 = 1时,系统的相图
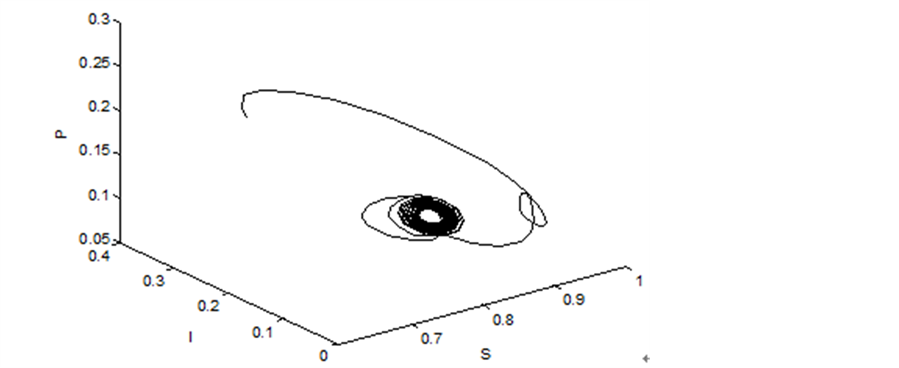
Figure 3. τ0 = 15, the phase diagram of the system
图3. 当τ0 = 15时,系统的相图

Figure 4. τ0 = 15, the plan graph of the system
图4. 当τ0 = 15时,系统的相图
4. 总结与分析
本文主要讨论了具有Holling II型功能反应的时滞生态传染病系统,分析了系统在平衡点处的局部稳定性的性质。选取时滞 为分支参数,当满足条件
为分支参数,当满足条件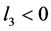 或
或 ,
, ,
, ,
,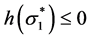 时,对
时,对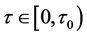 ,
,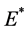 是渐进稳定的,此时捕食者种群、染病食饵种群和易染病食饵种群会处于一个长期平稳的发展阶段,疾病的传播得到了控制;随着
是渐进稳定的,此时捕食者种群、染病食饵种群和易染病食饵种群会处于一个长期平稳的发展阶段,疾病的传播得到了控制;随着 的增加,平衡点将会失去稳定性,且在
的增加,平衡点将会失去稳定性,且在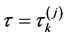 时产生Hopf分支,此时疾病并不会得到控制,会周期性的影响食饵种群和捕食者种群的数量。最后进行了相应的数值模拟来验证所得的结论。
时产生Hopf分支,此时疾病并不会得到控制,会周期性的影响食饵种群和捕食者种群的数量。最后进行了相应的数值模拟来验证所得的结论。
文章引用
龚天蓉,赵维锐. 具有时滞的生态传染病系统的稳定性分析
Stability of an Eco-Epidemiological System with Delay[J]. 自然科学, 2016, 04(02): 103-109. http://dx.doi.org/10.12677/OJNS.2016.42012
参考文献 (References)
- 1. Sasmal, S.K. and Chattopadhyay, J. (2013) An Eco-Epidemiological System with Infected Prey and Predator Subject to the Weak Allee Effect. Mathematical Biosciences, 246, 260-271. http://dx.doi.org/10.1016/j.mbs.2013.10.005
- 2. Biswas, S., Sasmal, S.K. and Samanta, S. (2015) A Delay Eco-Epidemiological System with Infected Prey and Predator Subject to the Weak Allee Effect. Mathematical Biosciences, 263, 198-208. http://dx.doi.org/10.1016/j.mbs.2015.02.013
- 3. Yuan, S.L. and Zhang, F.Q. (2010) Stability and Global Hopf Bifurcation in a Delayed Predator-Prey System. Nonlinear Analysis: Real World Applications, 11, 959-977. http://dx.doi.org/10.1016/j.nonrwa.2009.01.038
- 4. Song, Y.L., Han, M.A. and Wei, J.J. (2005) Stability and Hopf Bifurcation Analysis on a Simplified BAM Neural Network with Delays. Physica D, 200, 185-204. http://dx.doi.org/10.1016/j.physd.2004.10.010
- 5. Song, Y.L. and Wei, J.J. (2005) Local Hopf Bifurcation and Global Periodic Solutions in a Delayed Predator-Prey System. Journal of Mathematical Analysis and Applications, 301, 1-21. http://dx.doi.org/10.1016/j.jmaa.2004.06.056
- 6. Hu, G.P. and Li, X.L. (2012) Stability and Hopf Bifurcation for a Delayed Predator-Prey Model with Disease in the Prey. Chaos, Solitons & Fractals, 45, 229-237. http://dx.doi.org/10.1016/j.chaos.2011.11.011
- 7. Kang, A., Xue, Y. and Jin, Z. (2008) Dynamic Behavior of an Eco-Epidemic System with Impulsive Birth. Journal of Mathematical Analysis and Applications, 45, 783-795. http://dx.doi.org/10.1016/j.jmaa.2008.04.043
- 8. Zhang, J.F., Li, W.T. and Yan, X.P. (2008) Hopf Bifurcation and Stability of Periodic Solution in a Delayed Eco- Epidemiological System. Applied Mathematics and Computation, 198, 865-876. http://dx.doi.org/10.1016/j.amc.2007.09.045
- 9. Peterson, R.O. and Page, R.E. (1987) Wolf Density as a Perdictor of Predation Rate. Swedish Wildlife Research, 1, 771.
- 10. Hale, J.K. (1977) Theory of Functional Differential Equations. Springer-Verlag, Berlin. http://dx.doi.org/10.1007/978-1-4612-9892-2