NP-PCR5融合算法及应用 NP-PCR5 Fusion Algorithm and Application

doi:10.12677/JSTA.2019.72002

Journal of Sensor Technology and Application
Vol. 07 No. 02 ( 2019 ), Article ID: 29424 , 6 pages
10.12677/JSTA.2019.72002

NP-PCR5 Fusion Algorithm and Application

Xin Guan, Jing Zhao, Haiqiao Liu

●How to Cite this Article

Navy Aviation University, Yantai Shandong

Received: Mar. 1^st, 2019; accepted: Mar. 19^th, 2019; published: Mar. 26^th, 2019

ABSTRACT

This paper combines the Neutrosophic Probability theory with DSM theory, and proposes a new fusion algorithm NP-PCR5 based on the Neutrosophic Probability (NP) and Proportional Conflict Redistribution Rules (PCR). Through theoretical analysis, formula derivation and comparative experiments, the feasibility and effectiveness of the NP-PCR5 fusion algorithm in multi-sensor target recognition are proved.

Keywords:Neutrosophic Logic, Neutrosophic Measure, Neutrosophic Probability, PCR5

NP-PCR5融合算法及应用

关欣，赵静，刘海桥

海军航空大学，山东烟台

收稿日期：2019年3月1日；录用日期：2019年3月19日；发布日期：2019年3月26日

摘要

本文将中智理论与DSm理论相融合，基于中智概率(Neutrosophic Probability, NP)及成比例的冲突再分配规则(Proportional Conflict Redistribution Rules, PCR)提出了一种新的融合算法NP-PCR5，通过理论分析、公式推导、算例比较实验，证明了NP-PCR5融合算法在多传感器目标识别中应用的可行性和有效性。

关键词 :中智逻辑，中智度量，中智概率，PCR5

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

为了解决复杂环境因素给单一传感器带来的识别率过低的问题，多传感器信息融合技术应运而生。在现代战场复杂的电磁环境下，因受到噪声或干扰设备等影响，由不同传感器所得到的证据通常是模糊、不确定且不完全的，甚至会出现高度冲突的情况 [1] 。自2002年由法国学者Dezert和Smarandache所提出的DSm理论可以有效解决证据高度冲突情况下的信息融合问题，应用前景也十分的广泛，近年来得到了陆续的发展 [2] 。Dezert和Smarandache提出的成比例冲突再分配规则(Proportional Conflict Redistribution Rules, PCR)是将冲突信度按一定的比例关系分配至非空集部分，有效地解决了DSm理论由于引进交运算而造成的融合结果分类精细不利于判决的问题。

中智学是哲学的一个分支。英文Neutrosophy取自拉丁字根“neuter”(中性、中立)，1980年由Florentin Smarandache提出并创立，它主要研究中立性的起源、本质和范畴以及与不同思想观念的作用。中智学关心的是命题、理论、事物、概念或实体“A”和它的对立“Anti-A”、它的否定“Non-A”以及既不是“A”又不是“Anti-A”记为“Neut-A”三者之间的关系。

本文结合中智学研究的主题，将中智概率与从数学意义来看最有效及精确的冲突分配方法PCR5相结合，提出NP-PCR5融合算法，通过理论分析、公式推导、算例比较实验，验证了NP-PCR5融合算法在多传感器目标识别中应用的可行性和有效性。

2. 中智学

2.1. 中智逻辑

中智学是中智逻辑、中智集合、中智概率论和中智统计学的基础，并在各个学科中都有所应用。中智逻辑作为一个统一的逻辑，它是一种多值逻辑，包含了模糊逻辑、经典逻辑和其他特殊情况，中智逻辑具有以下几个特点 [3] ：

1) 不确定是由明确的不确定赋值来表述的；

2) 真、假以及不确定是相互独立的(三个不同的赋值)；

3) 它是一个量化逻辑，意味着真、假以及不确定可以用数值来表示；

4) 这种量化需要一个高度真实的间隔，这种间隔是真实数字间隔的一般化，可提供更广的解释框架；

5) 定义了许多新的连接(Neut-A, Anti-A, ……)。

在传统逻辑中，一个命题A要么是“真”要么是“假”。在模糊逻辑中，命题A允许以“真”的程度来表示“更真”或“次真”(也可以表示“更假”或“次假”)。在中智逻辑中，命题A可以表示为T%的“真”，I%的“不确定”和F%的“假”。这里 $(T, I, F) \in {‖ {}^{-}0, 1^{+} ‖}^{3}$ ，其中， $‖ {}^{-}0, 1^{+} ‖$ 是超实距离 [4] 。因此，三个赋值取值于超实距离 $‖ {}^{-}0, 1^{+} ‖$ 的子集，而不是 $[0, 1]$ 。该符号的特殊之处是它涉及到了三维空间。中智逻辑中命题A由三个真值构成，我们称之为中智值 [5] ，即

$N L (A) = (T (A), I (A), F (A))$ (1)

2.2. 中智度量

令X是一个中智空间， $Σ$ 是X的σ-中智代数。若，则A的中智度量v定义如下 [6] ：

$v : X \to R^{3},$

$v (A) = (m (A), m (n e u t A), m (a n t i A))$ (2)

其中， $a n t i A$ 称之为反-A，表示A的对立面； $n e u t A$ 称之为中智-A，表示既不是A也不是反-A；A满足 $A \subseteq X$ 且 $A \in \sum$ 。 $m (A)$ 、 $m (n e u t A)$ 、 $m (a n t i A)$ 分别表示A、中智-A及反-A的度量。

v是一个度量函数，满足以下两个性质：

1) $v (Φ) = (0, 0, 0)$ 。

2) 可数可加性：对于 $Σ$ 中所有不相交的可数集 ${A_{n}}_{n \in L}$ ，有下式成立：

$v (\underset{n \in L}{\cup} A_{n}) = (\sum_{n \in L} m (A_{n}), \sum_{n \in L} m (n e u t A_{n}), \sum_{n \in L} m (a n t i A_{n}) - (n - 1) m (X))$ (3)

其中，X表示整个中智空间，且

$\sum_{n \in L} m (a n t i A_{n}) - (n - 1) m (X) = m (X) - \sum_{n \in L} m (A_{n}) = m (\underset{n \in L}{\cap} A_{n})$ (4)

因此，中智度量空间可以用一个三维数组表示，即 $(X, Σ, v)$ 。

2.3. 中智度量与中智概率

根据中智逻辑 [7] 可知，若设X是一个中智度量空间，则

$0 \leq v (X) = (x_{1}, x_{2}, x_{3}) \leq 3$ (5)

其中， $v (X)$ 所包含的三个元素的和有以下三种情况：

1) 当三个元素 $x_{1}, x_{2}, x_{3}$ 相互独立时，满足 $0 \leq x_{1} + x_{2} + x_{3} \leq 3$ ；

2) 当三个元素 $x_{1}, x_{2}, x_{3}$ 中有两个元素相互独立时，满足 $0 \leq x_{1} + x_{2} + x_{3} \leq 2$ ；

3) 当三个元素 $x_{1}, x_{2}, x_{3}$ 相关时，满足 $0 \leq x_{1} + x_{2} + x_{3} \leq 1$ 。

当 $v (X) = (m (X), m (n e u t X), m (a n t i X)) = (x_{1}, x_{2}, x_{3})$ 满足 $x_{1} \geq 0, x_{2} \geq 0, x_{3} \geq 0$ 且 $x_{1} + x_{2} + x_{3} = 1$ 时，就称此种形式的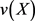是中智度量的归一化。

同理，中智概率(Neutrosophic Probability)的归一化形式可以表示为

$N P (A) = (m (A), m (n e u t A), m (a n t i A)) = (t, i, f)$ (6)

其中， $m (A) + m (n e u t A) + m (a n t i A) = 1$ ，t表示命题A发生的概率，i表示中智-A发生的概率，f表示命题A不发生的概率。

3. PCR5规则

PCR(成比例冲突再分配规则)是由Dezert和Smarandache提出来的 [8] ，在DSm理论中共包含PCR1~PCR5五种规则，它们的不同主要在于冲突的比例再分配形式，其中，目前PCR5是从数学意义来讲最有效以及最精确的冲突分配方法。PCR5理论将辨识框架中的单焦元看作冲突信息的来源，把组合后的冲突信息都是按照单焦元的置信指派进行再分配。

两独立证据源的PCR5规则简要介绍如下：

$m_{12} (X_{i}) = \sum_{\begin{matrix} Y, Z \in G^{Θ} and Y, Z \neq \emptyset \\ Y \cap Z = X_{i} \end{matrix}} m_{1} (Y) \cdot m_{2} (Z)$ (7)

$\begin{matrix} m_{12} (X_{i}) + \sum_{\begin{array}{l} X_{j} \in G^{Θ} and i \neq j \\ X_{i} \cap X_{j} = \emptyset \end{array}} [\frac{m_{1} {(X_{i})}^{2} m_{2} (X_{j})}{m_{1} (X_{i}) + m_{2} (X_{j})} + \frac{m_{2} {(X_{i})}^{2} m_{1} (X_{j})}{m_{2} (X_{i}) + m_{1} (X_{j})}] & X_{i} \in G^{Θ} and X_{i} \neq \emptyset \\ 0 & X_{i} = \emptyset \end{matrix}$ (8)

其中， $m_{1} (\cdot)$ 和 $m_{2} (\cdot)$ 表示两个独立证据源的基本概率分配， $G^{Θ}$ 表示广义幂集空间，式(8)中所有分式的分母不为0，如果分母为0，则分式不再使用。

4. NP-PCR5融合算法

定理：假设两个独立证据源所获得的信息分别为 $N P_{1} (t_{1}, i_{1}, f_{1})$ 和 $N P_{2} (t_{2}, i_{2}, f_{2})$ ，由PCR5规则有

$[N P_{1} \oplus N P_{2}] (t) = t_{1} t_{2} + (\frac{t_{1}^{2} i_{2}}{t_{1} + i_{2}} + \frac{t_{2}^{2} i_{1}}{t_{2} + i_{1}}) + (\frac{t_{1}^{2} f_{2}}{t_{1} + f_{2}} + \frac{t_{2}^{2} f_{1}}{t_{2} + f_{1}})$ (9)

证明：因为根据PCR5规则，冲突信度 $t_{1} i_{2}$ 应该按照局部冲突中 $t_{1}$ 和 $i_{2}$ 原有的信度比例进行再分配，所以有

$\frac{x_{1}}{t_{1}} = \frac{y_{1}}{i_{2}} = \frac{t_{1} i_{2}}{t_{1} + i_{2}}$ (10)

因此

$x_{1} = \frac{t_{1}^{2} i_{2}}{t_{1} + i_{2}}$ ， $y_{1} = \frac{t_{1} i_{2}^{2}}{t_{1} + i_{2}}$ (11)

同理，冲突信度按照局部冲突中 $t_{2}$ 和 $i_{1}$ 原有的信度比例进行再分配，有

$\frac{x_{2}}{t_{2}} = \frac{y_{2}}{i_{1}} = \frac{t_{2} i_{1}}{t_{2} + i_{1}}$ (12)

则

$x_{2} = \frac{t_{2}^{2} i_{1}}{t_{2} + i_{1}}$ ， $y_{2} = \frac{t_{2} i_{1}^{2}}{t_{2} + i_{1}}$ (13)

同样地，冲突信度 $t_{1} f_{2}$ 按比例进行再分配后，有

$\frac{x_{3}}{t_{1}} = \frac{z_{1}}{f_{2}} = \frac{t_{1} f_{2}}{t_{1} + f_{2}}$ (14)

则

$x_{3} = \frac{t_{1}^{2} f_{2}}{t_{1} + f_{2}}$ ， (15)

冲突信度 $t_{2} f_{1}$ 按比例进行再分配后，有

$\frac{x_{4}}{t_{2}} = \frac{z_{2}}{f_{1}} = \frac{t_{2} f_{1}}{t_{2} + f_{1}}$ (16)

则

$x_{4} = \frac{t_{2}^{2} f_{1}}{t_{2} + f_{1}}$ ， $z_{2} = \frac{t_{2} f_{1}^{2}}{t_{2} + f_{1}}$ (17)

冲突信度 $i_{1} f_{2}$ 按比例进行再分配后，有

$\frac{y_{3}}{i_{1}} = \frac{z_{3}}{f_{2}} = \frac{i_{1} f_{2}}{i_{1} + f_{2}}$ (18)

则

$y_{3} = \frac{i_{1}^{2} f_{2}}{i_{1} + f_{2}}$ ， $z_{3} = \frac{i_{1} f_{2}^{2}}{i_{1} + f_{2}}$ (19)

冲突信度 $i_{2} f_{1}$ 按比例进行再分配后，有

$\frac{y_{4}}{i_{2}} = \frac{z_{4}}{f_{1}} = \frac{i_{2} f_{1}}{i_{2} + f_{1}}$ (20)

则

$y_{4} = \frac{i_{2}^{2} f_{1}}{i_{2} + f_{1}}$ ， $z_{3} = \frac{i_{2} f_{1}^{2}}{i_{2} + f_{1}}$ (21)

所以，由式(7)和式(8)可得式(9)，即

成立。

同理，可得

$[N P_{1} \oplus N P_{2}] (i) = i_{1} i_{2} + (\frac{i_{1}^{2} t_{2}}{i_{1} + t_{2}} + \frac{i_{2}^{2} t_{1}}{i_{2} + t_{1}}) + (\frac{i_{1}^{2} f_{2}}{i_{1} + f_{2}} + \frac{i_{2}^{2} f_{1}}{i_{2} + f_{1}})$ (22)

$[N P_{1} \oplus N P_{2}] (f) = f_{1} f_{2} + (\frac{f_{1}^{2} t_{2}}{f_{1} + t_{2}} + \frac{f_{2}^{2} t_{1}}{f_{2} + t_{1}}) + (\frac{f_{1}^{2} i_{2}}{f_{1} + i_{2}} + \frac{f_{2}^{2} i_{1}}{f_{2} + i_{1}})$ (23)

5. 算例分析

假设用于识别目标身份的系统中有两种传感器，对空中目标进行敌我识别时的框架为 $θ = (T, I, F)$ ，其中，T代表我机、I代表中立、F代表敌机。假设通过两证据源采集到的信息如表1所示，试判定目标的类别。

Table 1. Data collection

表1. 采集数据表

由题可知，两证据源所提供的信息是高度冲突的，根据经验，通过观察可看出证据源1所提供的信息不确定性的概率是0.1，而证据源2所提供的信息不确定性的概率是0.3，因此，根据先验知识可知，证据源1提供信息的可信度高于证据源2，所以判定目标的类别为我机。

下面将用本文所述的NP-PCR5方法判定目标类型，观察结果是否一致。

由题可知，两证据源所得信息的中智概率分别为和 $N P_{2} = (t_{2}, i_{2}, f_{2}) = (0.2, 0.3, 0.5)$ ，将 $(t_{1}, i_{1}, f_{1})$ 和 $(t_{2}, i_{2}, f_{2})$ 分别代入式(9)、式(22)和式(23)可得

$[N P_{1} \oplus N P_{2}] (t) = 0.6 (0.2) + (\frac{{0.6}^{2} (0.3)}{0.6 + 0.3} + \frac{{0.2}^{2} (0.1)}{0.2 + 0.1}) + (\frac{{0.6}^{2} (0.5)}{0.6 + 0.5} + \frac{{0.2}^{2} (0.3)}{0.2 + 0.3}) \approx 0.44$

$[N P_{1} \oplus N P_{2}] (i) = 0.1 (0.3) + (\frac{{0.1}^{2} (0.2)}{0.1 + 0.2} + \frac{{0.3}^{2} (0.6)}{0.3 + 0.6}) + (\frac{{0.1}^{2} (0.5)}{0.1 + 0.5} + \frac{{0.3}^{2} (0.3)}{0.3 + 0.3}) \approx 0.15$

$[N P_{1} \oplus N P_{2}] (f) = 0.3 (0.5) + (\frac{{0.3}^{2} (0.2)}{0.3 + 0.2} + \frac{{0.5}^{2} (0.6)}{0.5 + 0.6}) + (\frac{{0.3}^{2} (0.3)}{0.3 + 0.3} + \frac{{0.5}^{2} (0.1)}{0.5 + 0.1}) \approx 0.41$

通过上述算例表明，虽然在两证据源提供信息高度冲突的情况下，NP-PCR5融合算法所得到的识别结果仍然是我机，且通过该融合算法降低了证据源2的不确定性概率，融合后不确定性概率降至0.15，因此，通过NP-PCR5融合算法对目标进行识别时，识别置信度高，且会降低不确定性，可以合理且客观地反映事实。

6. 结论

将中智概率与PCR5规则进行融合的算法可以用于目标识别，且适用于两证据源所提供的信息高度冲突的情况下。本文通过理论分析、公式推导、算例实验，对NP-PCR5融合算法识别置信度高、可降低不确定性概率的特点进行了说明，并证明了NP-PCR5融合算法在多传感器目标识别中应用的可行性和有效性。

基金项目

国防科技卓越青年人才基金(2017-JCJQ-ZQ-003)，泰山学者工程专项经费(ts201712072)，国家自然科学基金(61501488)资助课题。

文章引用

关欣,赵静,刘海桥. NP-PCR5融合算法及应用
NP-PCR5 Fusion Algorithm and Application[J]. 传感器技术与应用, 2019, 07(02): 13-18. https://doi.org/10.12677/JSTA.2019.72002

参考文献

1. 何友, 王国宏, 关欣, 等. 信息融合理论及应用[M]. 北京: 电子工业出版社, 2010.

2. 黄心汉, 李新德, 译. DSmT理论及其在信息融合中的应用[M]. 北京: 国防工业出版社, 2011.

3. Smarandache, F. (1998) Neutroso-phy. Neutrosophic Probability, Set, and Logic. American Research Press, Rehoboth, USA, 105.

4. Vasantha Kan-dasamy, W.B. and Smarandache, F. (2003) Fuzzy Cognitive Maps and Neutrosophic Cognitive Maps. Xiquan, Phoenix, 211 p.

5. Smarandache, F. (2015) (t,i,f)-Neutrosophic Structures and I-Neutrosophic Structures. Neutrosophic Sets and Systems, 8, 3-10.

6. Smarandache, F. (2013) Introduction of Neutrosophic Measure, Neutrosophic Integral, and Neutrosophic Probability. Sytech, Craiova.

7. Smarandache, F. (2013) N-Valued Refined Neutrosophic Logic and its Applications in Physics. Progress in Physics, 4, 143-146.

8. Smarandache, F. and Dezert, J. (2005) Information Fusion Based on New Proportional Conflict Redistribution Rules. Proceedings of the 8th International Conference on Information Fusion, Philadelphia, 25-29 July 2005.

期刊菜单