Pure Mathematics
Vol.07 No.03(2017), Article ID:20634,7
pages
10.12677/PM.2017.73025
The Minimal Trees of Steiner Wiener Index with Given Matching Number
Zhongzhu Liu, Li He
Mathematics and Big Data College, Huizhou University, Huizhou Guangdong

Received: May. 4th, 2017; accepted: May 19th, 2017; published: May 24th, 2017

ABSTRACT
The Steiner distance  of a vertex set S is defined as the minimum number of edges of a tree whose vertex set contains a vertex set S, and the Steiner k-Wiener index
of a vertex set S is defined as the minimum number of edges of a tree whose vertex set contains a vertex set S, and the Steiner k-Wiener index 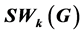 of G is defined as the sum of
of G is defined as the sum of 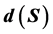 among all possible k-vertex set S of G. In this paper, we determine the minimal value of
among all possible k-vertex set S of G. In this paper, we determine the minimal value of 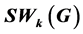 in the class of trees with given matching number.
in the class of trees with given matching number.
Keywords:Steiner Distance, Tree, Matching Number

给定匹配数的Steiner Wiener指数极小树
刘中柱,何莉
惠州学院数学与大数据学院,广东 惠州

收稿日期:2017年5月4日;录用日期:2017年5月19日;发布日期:2017年5月24日

摘要
本文讨论了给定匹配数的树中k-Steiner Wiener指数的极小值,并刻画了极图。图 的k-Steiner Wiener指数定义为图
的k-Steiner Wiener指数定义为图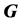 中任意k-点集
中任意k-点集 的Steiner距离
的Steiner距离 的和,而点集
的和,而点集 的Steiner距离
的Steiner距离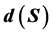 是包含点集
是包含点集 的最小子树的边的数目。
的最小子树的边的数目。
关键词 :Steiner距离,树,匹配数

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
设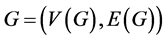 是一个简单连通图,其中
是一个简单连通图,其中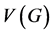 ,
, 分别是图
分别是图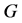 的点集与边集,且
的点集与边集,且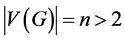 ,
, 。图
。图 中任意两点
中任意两点 ,
, 间的距离
间的距离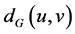 定义为连通
定义为连通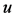 ,
, 的最短路的长度,Wiener指数
的最短路的长度,Wiener指数 定义为:
定义为:
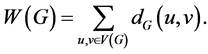
在化学理论中,基于分子图的顶点间距离的拓扑指数对刻画分子图以及建立分子结构和特征间的关系有重要作用,同时被广泛用于预测化合物的物理化学性质和生物活性。Wiener指数是研究最为广泛的拓扑指数之一,它用于考察烷烃的沸点与分子结构的关系,同时也用于分析交通网络与社交网络。相关的结果参考文献 [1] - [16] 。
在任二点距离的基础上,提出了图的点集的广义距离:点集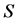 的Steiner距离
的Steiner距离 定义为图
定义为图 中包含点集
中包含点集 的最小子树的边数,Steiner距离是经典的组合优化问题,最早可以追溯到17世纪初。1634年,数学家Fermat提出这样一个问题:在欧氏平面上有三个点,寻找一个点使得由该点连接三个点的距离之和最小。后经多位数学家扩展补充,最后以瑞士数学家Steiner的名字命名为Steiner问题。由于Steiner距离在现代生产生活中应用十分广泛,因此多年来是研究的热点。本文讨论图的Steiner距离问题。
的最小子树的边数,Steiner距离是经典的组合优化问题,最早可以追溯到17世纪初。1634年,数学家Fermat提出这样一个问题:在欧氏平面上有三个点,寻找一个点使得由该点连接三个点的距离之和最小。后经多位数学家扩展补充,最后以瑞士数学家Steiner的名字命名为Steiner问题。由于Steiner距离在现代生产生活中应用十分广泛,因此多年来是研究的热点。本文讨论图的Steiner距离问题。
若 是连通图,则
是连通图,则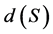 等于
等于 生成树的边数,即
生成树的边数,即 .Dankelmann, Oellermann, Swart [17] 提出了k-Steiner平均距离
.Dankelmann, Oellermann, Swart [17] 提出了k-Steiner平均距离 的概念,其中
的概念,其中

随后李学良,毛亚平,Gutman在文献 [18] 中提出了k-Steiner Wiener指数 的概念,其中
的概念,其中
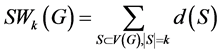
且
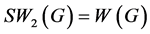
Dankelmann, Oellermann, Swart在文献 [17] 中得到给定点数的树中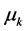 的上下界,李学良等人在文献 [18] 中给出了树的
的上下界,李学良等人在文献 [18] 中给出了树的 指数计算公式,M. Kovse [19] 进一步得到树的
指数计算公式,M. Kovse [19] 进一步得到树的 的点和边的表达公式。与Steiner距离的拓扑指数相关的结果可参考文献 [20] - [25] 。由于图
的点和边的表达公式。与Steiner距离的拓扑指数相关的结果可参考文献 [20] - [25] 。由于图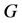 的
的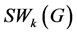 计算是NP完全问题 [24] ,讨论特殊图类的上下界与极图问题显得十分重要,本文将重点讨论给定匹配数的树的下界与极图。
计算是NP完全问题 [24] ,讨论特殊图类的上下界与极图问题显得十分重要,本文将重点讨论给定匹配数的树的下界与极图。
2. 预备知识
图中不相邻的边的集合称为图的一个匹配,而边数最多的匹配称为图的最大匹配。设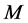 是图
是图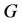 的一个最大匹配,称
的一个最大匹配,称 中元素的个数为图
中元素的个数为图 的匹配数,若
的匹配数,若 饱和图
饱和图 的每个顶点,称图
的每个顶点,称图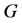 为完美匹配图。令
为完美匹配图。令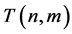 为
为 个顶点,且匹配数为
个顶点,且匹配数为 的树的集合,其中
的树的集合,其中 .
.
为了进一步讨论Steiner Wiener指数,根据Steiner距离的定义,得到以下引理:
引理2.1. 若 是连通图
是连通图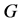 中的任两点,且
中的任两点,且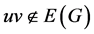 ,则
,则 ,其中
,其中 是在
是在 中增加边
中增加边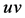 得到的新图。
得到的新图。
引理2.2. 若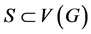 ,
, 是连通的,则
是连通的,则 .
.
M. Kovse [19] 给出以下关于树的Steiner Wiener指数边的表达公式。
引理2.3. 若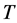 是
是 个顶点的树,则
个顶点的树,则

其中 分别是
分别是 后两个连通分支的点数。
后两个连通分支的点数。
证明:由 [19] 的结果可知

证毕。
3. 主要结果
引理3.1. 若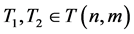 ,且
,且 ,如图1 (Figure 1)所示,令
,如图1 (Figure 1)所示,令 到
到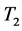 的变换称为I-变换,则对任意正整数
的变换称为I-变换,则对任意正整数 ,有
,有
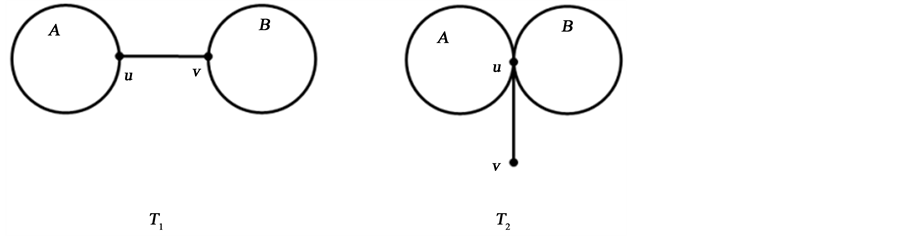
Figure 1. The I-transformation of Lemma 3.1
图1. 引理3.1中的I-变换
证明:由于树的每一条边都是割边,取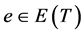 ,则不妨设
,则不妨设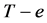 的二个连通块的点数分别为
的二个连通块的点数分别为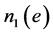 ,
,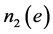 ,则有
,则有 ,
, ,若
,若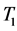 ,
, 中的点与边取相同的标号,由引理2.3可知:
中的点与边取相同的标号,由引理2.3可知:

任取边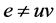 ,则有
,则有
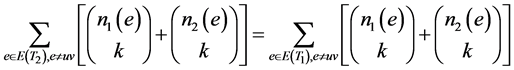
令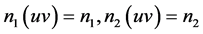 ,由于
,由于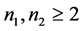 ,不妨设
,不妨设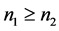 ,从而有
,从而有
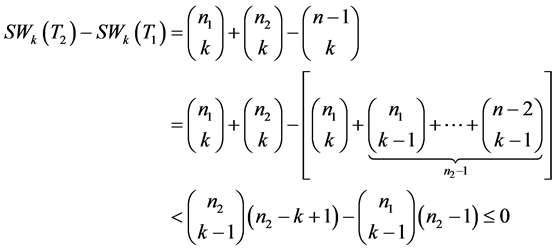
证毕。
引理3.2. 若 ,且
,且 ,如图2 (Figure 2)所示,令
,如图2 (Figure 2)所示,令 到
到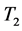 的变换称为II-变换,对任意正整数
的变换称为II-变换,对任意正整数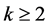 ,有
,有

证明:由于树的每一条边都是割边,取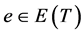 ,则不妨设
,则不妨设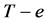 的二个连通块的点数分别为
的二个连通块的点数分别为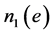 ,
, ,则有
,则有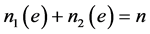 ,
, ,若
,若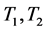 中的点与边取相同的标号,由引理2.3可知:
中的点与边取相同的标号,由引理2.3可知:

任取边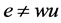 ,则有
,则有
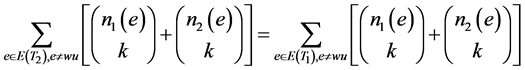
令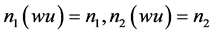 ,由于
,由于 ,从而有
,从而有
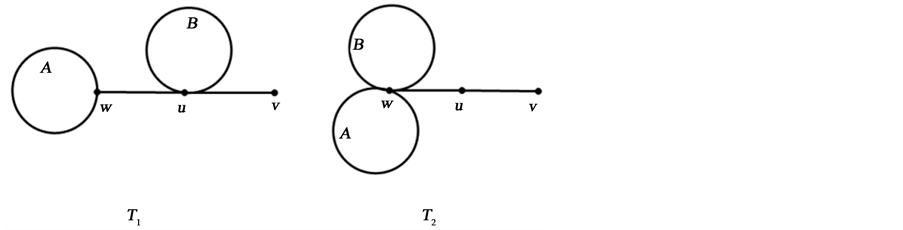
Figure 2. The II-transformation of Lemma 3.2
图2. 引理3.2中的II-变换
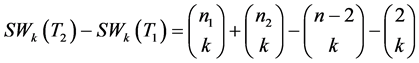
以下对 分情况讨论:
分情况讨论:
情况1:若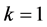 或
或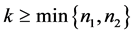 ,显然有
,显然有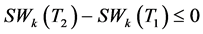 .
.
情况2:若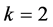 ,则有
,则有

情况3:若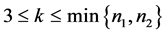 ,不妨设
,不妨设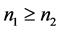 ,则有
,则有
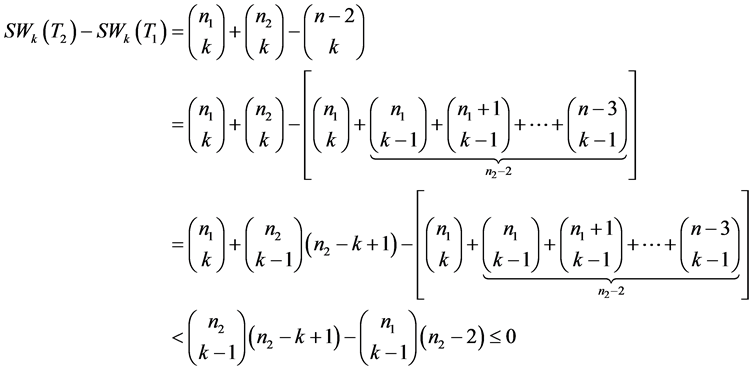
综合情况1、2、3,得到结果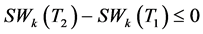 。证毕。
。证毕。
如图3 (Figure 3)所示,令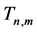 是对星图
是对星图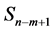 中的
中的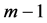 个悬挂点分别与一个新的点连边得到的树,易知
个悬挂点分别与一个新的点连边得到的树,易知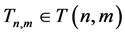 ,从而对任一树
,从而对任一树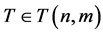 且
且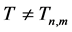 ,可通过引理3.1和3.2当中的I-,II-变换,逐步变换成
,可通过引理3.1和3.2当中的I-,II-变换,逐步变换成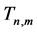 ,从而有以下定理:
,从而有以下定理:
定理3.1. 若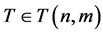 ,对任意正整数
,对任意正整数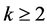 ,有
,有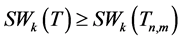

Figure 3. The extremal graph  of Theorem 3.1
of Theorem 3.1
图3. 定理3.1中的极图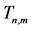
基金项目
本文受广东省自然科学基金(No. 2014A030310119)、国家社会科学基金(No. 15BTJ024)和惠州市科技创新基金(No. 2014B020004027)资助。
文章引用
刘中柱,何莉. 给定匹配数的Steiner Wiener指数极小树
The Minimal Trees of Steiner Wiener Index with Given Matching Number[J]. 理论数学, 2017, 07(03): 193-199. http://dx.doi.org/10.12677/PM.2017.73025
参考文献 (References)
- 1. da Fonseca, C.M., Ghebleh, M., Kanso, A. and Stevanovic, D. (2014) Counterexamples to a Conjecture on Wiener Index of Common Neighborhood Graphs. MATCH Communications in Mathematical and in Computer Chemistry, 72, 333-338.
- 2. Dobrynin, A., Entringer, R. and Gutman, I. (2001) Wiener Index of Trees: Theory and Application. Acta Applicandae Mathematicae, 66, 211-249.
- 3. Du, Z. and Zhou, B. (2010) Minimum Wiener Indices of Trees and Unicyclic Graphs of Given Matching Number. MATCH Communications in Mathematical and in Computer Chemistry, 63, 101-112.
- 4. Goddard, W. and Oellermann, O.R. (2011) Distance in Graphs. In: Dehmer, M., Ed., Structural Analysis of Complex Networks, Birkhauser, Dordrecht, 49-72. https://doi.org/10.1007/978-0-8176-4789-6_3
- 5. Gutman, I., Furtula, B. and Li, X. (2015) Multicenter Wiener Indices and Their Applications. Journal of the Serbian Chemical Society, 80, 1009-1017. https://doi.org/10.2298/JSC150126015G
- 6. Gutman, I., Klavzar, S. and Mohar, B. (1997) Fifty Years of the Wiener Index. MATCH Communications in Mathematical and in Computer Chemistry, 35, 1-159.
- 7. Gutman, I. and Zhang, S. (2006) Graph Connectivity and Wiener Index. Bulletin Classe des Sciences Mathematiques et Natturalles, 133, 1-5.
- 8. Yeh, H.-G. and Chang, G.J. (1996) Weighted Connected Domination and Steiner Trees in Distance-Hereditary Graphs. In: Graph Theory-Combinatorics and Computer Science, Vol. 1120 of the series Lecture Notes in Computer Science, 48-52.
- 9. Jin, Y.L. and Zhang, X.D. (2013) On Two Conjectures of the Wiener Index. MATCH Communications in Mathematical and in Computer Chemistry, 70, 583-589.
- 10. Kovse, M. (2016) Vertex Decomposition of Steiner Wiener Index and Steiner Betweenness Centrality. arxiv: 1605.00260
- 11. Oellermann, O.R. and Tian, S. (1990) Steiner Centers in Graphs. Journal of Graph Theory, 14, 585-597. https://doi.org/10.1002/jgt.3190140510
- 12. Rouvray, D.H. (2002) Harry in the Limelight: The Life and Times of Harry Wiener. In: Rouvray, D.H. and King, R.B. Eds., Topology in Chemistry—Discrete Mathematics of Molecules, Horwood, Chichester, 1-15.
- 13. Rouvray, D.H. (2002) The Rich Legacy of Half Century of the Wiener Index. In: Rouvray, D.H. and King, R.B., Eds., Topology in Chemistry—Discrete Mathematics of Molecules, Horwood, Chichester, 16-37.
- 14. Wiener, H. (1947) Structural Determination of Paraffin Boiling Points. Journal of the American Chemical Society, 69, 17-20. https://doi.org/10.1021/Ja01193a005
- 15. Tutte, W.T. (1947) The Factorization of Linear Graphs. Journal of the London Mathematical Society, 22, 107-111. https://doi.org/10.1112/jlms/s1-22.2.107
- 16. Xu, K., Liu, M., Das, K.C., Gutman, I. and Furtula, B. (2014) A Survey on Graphs Extremal with Respect to Distance-Based Topological Indices. MATCH Communications in Ma-thematical and in Computer Chemistry, 71, 461-508.
- 17. Dankelmann, P., Oellermann, O.R. and Swart, H.C. (1996) The Average Steiner Distance of a Graph. Journal of Graph Theory, 22, 15-22. https://doi.org/10.1002/(SICI)1097-0118(199605)22:1<15::AID-JGT3>3.0.CO;2-O
- 18. Li, X., Mao, Y. and Gutman, I. (2016) The Steiner Wiener Index of a Graph. Discussiones Mathematicae Graph Theory, 36, 455-465.
- 19. Kovse, M. (2016) Vertex Decomposition of the Steiner Wiener Index and the Steiner Betweenness Centrality. arXiv:1605.00260v2 [math.CO].
- 20. Ali, P., Dankelmann, P. and Mukwembi, S. (2012) Upper Bounds on the Steiner Diameter of a Graph. Discrete Applied Mathematics, 160, 1845-1850.
- 21. Caceresa, J., Marquezb, A. and Puertasa, M.L. (2008) Steiner Distance and Convexity in Graphs. European Journal of Combinatorics, 29, 726-736.
- 22. Chartrand, G., Oellermann, O.R., Tian, S. and Zou, H.B. (1989) Steiner Distance in Graphs. Časopis pro Pěstování Matematiky, 114, 399-410.
- 23. Dankelmann, P., Swart, H.C. and Oellermann, O.R. (1997) On the Average Steiner Distance of Graphs with Prescribed Properties. Discrete Applied Mathematics, 79, 91-103.
- 24. Garey, M.R. and Johnson, D.S. (1979) Computers and Intractability—A Guide to the Theory of NP-Completeness. Freeman, San Francisco, 208-209.
- 25. 刘中柱, 程晓胜. Steiner Wiener指数与图的参数[J]. 应用数学进展, 2016, 5(4): 747-453.