Pure Mathematics
Vol.
10
No.
04
(
2020
), Article ID:
35085
,
5
pages
10.12677/PM.2020.104041
Some Research on L-Semi-Topology Space
Fei Li, Peiyong Zhu
School of Mathematical Sciences, University of Electronic Science and Technology of China, Chengdu Sichuan

Received: Mar. 22nd, 2020; accepted: Apr. 9th, 2020; published: Apr. 17th, 2020

ABSTRACT
Firstly, we explore the properties of point set on L-semi-topology space, discuss the properties of L-semi-topology subspace, and then get some results in the L-semi-topology space. On this basis, we discuss the comparison of L-semi-topology and L-semi-topology; thus, L-semi-topology theory is further enriched.
Keywords:L-Semi-Topology, L-Semi-Topology Subspace, L-Semi Topological Basis, L-Semi Topology Comparison

关于L-半拓扑空间上的一些探究
李飞,朱培勇
电子科技大学数学科学学院,四川 成都

收稿日期:2020年3月22日;录用日期:2020年4月9日;发布日期:2020年4月17日

摘 要
本文首先对L-半拓扑空间中的点集性质进行了研究,然后对L-半拓扑子空间的性质进行了研究,得到了L-半拓扑空间中的一些结果,在此基础上对L-半拓扑的比较、L-半拓扑基进行了讨论,从而进一步地丰富了L-半拓扑空间理论。
关键词 :L-半拓扑,L-半拓扑子空间,L-半拓扑基,L-半拓扑的比较

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言与预备知识
匈牙利数学家A. Csaszar 2002年在文献 [1] 中提出广义拓扑空间的概念,并且对广义拓扑空间的性质进行研究,此后不少学者也积极投入,例如文献 [2] - [9],在广义拓扑空间的点集性质、映射性质以及收敛性质等方面取得了一系列的研究成果。由于广义拓扑实际上是一类半拓扑,2015年文献 [10] 把广义拓扑重新命名为上半拓扑,进而引入了下半拓扑的概念,并且获得了关于下半拓扑中的一些很有意义的结果,在此,一个问题自然地被提出:
问题 能否类比文献 [10],将拓扑定义中(O1)、(O2)、(O3)三个条件(参见文献 [11])重新组合,将其重新分成两个半拓扑(左半拓扑和右半拓扑),进而得到一些比拓扑空间理论更弱的一些数学结果?
关于这个问题,文献 [12] [13] [14] [15] 做了一些工作。本文将在文献 [15] 的基础上对L-半拓扑进行更进一步研究。主要讨论了L-半拓扑空间中的点集性质、L-半拓扑的比较、L-半拓扑基。
下面是文献 [15] 引入关于L-半拓扑空间的一些基本概念。
1) 设X是任一非空集合, 是X的一些子集构成的集族,如果下列条件被满足:
(O1) ;(O2) 若 ,则 (其中 为任意指标集)。则称 为集合X的L-半拓扑,并且称有序偶 为一个L-半拓扑空间,集族 中的每一个集合都称为L-半拓扑空间
的L-开集。
2) 设 为L-半拓扑空间, ,如果 ,使得 ,则称U为点x的一个L-邻域,x点邻域的全体称为点x的L-邻域系,记作 ,并称 为由L-半拓扑 导出
的X的L-邻域系。
3) 设 为L-半拓扑空间, ,若 (即 ,使得 ),则称点x为点集A的L-内点。点集A的内点的全体称为A的内部,记为 或 。
4) 设 为L-半拓扑空间, ,如果 ,有 ,则称x为点集A的L-聚点,点集A的聚点的全体称为A的L-导集,记为 。
5) 设 为L-半拓扑空间, ,记 ,则称 为A的L-闭包。
6) 设 为L-半拓扑空间, 。若 ,则称F为X的L-闭集。
7) 设A为X中任意非空子集,并记 ,则 为A上的一个L-半拓扑,为此,称 为X上L-半拓扑 的一个子拓扑。其中 称为是 的L-半拓扑子空间,
为了方便,常常简称A为X的L-子空间。
如果没有特别声明,本文所涉及的一切概念、记号等都取自于文献 [15] 或者文献 [11]。
2. 关于L-半拓扑空间中的基本点集
首先,在文献 [15] 的基础上,我们有如下进一步的结果:
定理2.1 集合Χ上的任意两个L-半拓扑的交也是Χ上的一个L-半拓扑;集合Χ上的任意两个L-半拓扑的并不一定是Χ上的一个L-半拓扑。
证明:因为
且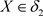 ,则
,则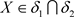 ;
;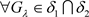 ,有
,有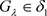 且
且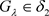 ,则
,则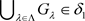 且
且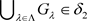 ,故
,故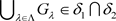 。因此两个L-半拓扑的交仍是Χ上的一个L-半拓扑。
。因此两个L-半拓扑的交仍是Χ上的一个L-半拓扑。
下面用反例说明:集合Χ上的任意两个L-半拓扑的并不一定是Χ上的一个L-半拓扑。
事实上,可取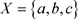 ,
,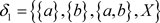 ,
,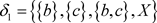 ,则
,则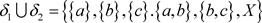 。显然,
。显然,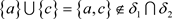 ,故
,故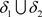 不是一个L-半拓扑。
不是一个L-半拓扑。
定理2.2 设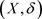 为L-半拓扑空间,
为L-半拓扑空间,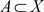 ,则(1)
,则(1)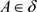 当且仅当
当且仅当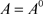 ;(2)
;(2) 必为闭集;(3)
必为闭集;(3)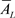 等于包含A的一切L-闭集的交。
等于包含A的一切L-闭集的交。
证明:1) (必要性) 因为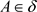 ,则对
,则对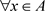 ,
,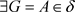 ,使得
,使得 ,故x是A的L-内点,所以,
,故x是A的L-内点,所以,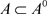 。又因
。又因 ,故有
,故有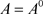 ;(充分性)
;(充分性)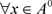 ,即x是A的L-内点,故
,即x是A的L-内点,故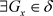 ,使得
,使得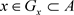 。因此,
。因此,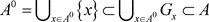 。又因
。又因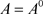 ,故
,故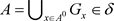 。
。
2) 反证:若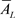 不是闭集,则由文献 [15] 定理2.5,有
不是闭集,则由文献 [15] 定理2.5,有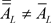 ;但又由文献 [15] 定理2.4的(LC3),有
;但又由文献 [15] 定理2.4的(LC3),有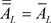 ,这就产生矛盾。所以,
,这就产生矛盾。所以, 必为闭集。
必为闭集。
3) 因为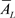 是L-闭集并且
是L-闭集并且 ,则
,则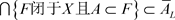 ;反过来,还需证明:
;反过来,还需证明: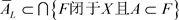 ,即需证:任何包含A的L-闭集F,必有
,即需证:任何包含A的L-闭集F,必有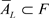 。事实上,如果存在L-闭集
。事实上,如果存在L-闭集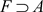 ,但
,但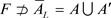 ,则
,则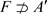 。取
。取 ,因为
,因为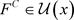 ,所以
,所以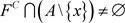 ,故
,故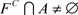 。这与
。这与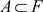 矛盾。即
矛盾。即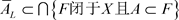 ,从而
,从而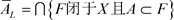 。
。
下面是关于子空间的一个结果:
定理2.3 设A为X的L-子空间,B为A的L-子空间,则B为X的L-子空间。
证明:设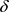 为X上的一个L-半拓扑并且
为X上的一个L-半拓扑并且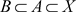 ,我们只需证明
,我们只需证明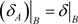 。事实上
。事实上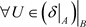 ,
,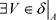 ,使得
,使得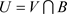 。又对于
。又对于 ,
,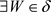 ,使得
,使得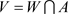 。从而
。从而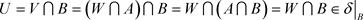 。所以
。所以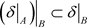 。
。
反过来,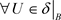 ,
,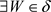 ,使得
,使得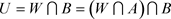 ,即
,即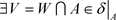 使得
使得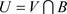 ,即
,即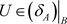 。从而
。从而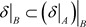 。因此
。因此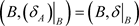 是
是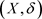 的L-子空间。
的L-子空间。
作为这一节最后,我们用下面例子说明:点x的L-邻域,未必一定是包含x的L-开集:
例2.4 设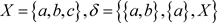 ,容易验证:
,容易验证: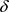 是X上一个L-半拓扑,且
是X上一个L-半拓扑,且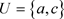 为点 的一个邻域,但U不是L-半拓扑空间
为点 的一个邻域,但U不是L-半拓扑空间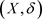 中的L-开集。
中的L-开集。
3. L-半拓扑的比较
定义3.1 设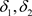 是Χ上的两个L-半拓扑,如果
是Χ上的两个L-半拓扑,如果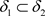 ,则称
,则称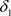 是比
是比 更粗的L-半拓扑,或称
更粗的L-半拓扑,或称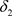 是比
是比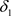 更细的L-半拓扑。
更细的L-半拓扑。
定理3.1 设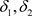 是Χ上的两个L-半拓扑,
是Χ上的两个L-半拓扑,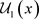 与
与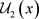 分别为 关于
分别为 关于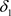 与
与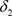 的邻域系,则
的邻域系,则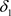 是比
是比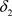 更粗的拓扑当且仅当
更粗的拓扑当且仅当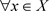 ,
,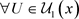 ,
,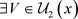 使得
使得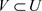 。
。
证明:(必要性) 设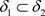 ,
,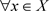 ,
,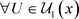 ,
,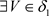 ,使
,使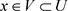 ,因为
,因为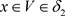 ,故
,故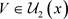 ,有
,有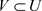 。
。
(充分性) 若
若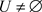 ,则
,则 有
有 。由已知,
。由已知,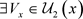 ,有
,有 。因此
。因此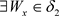 ,使得
,使得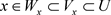 ,所以
,所以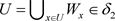 ,从而
,从而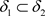 。
。
推论3.2 设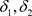 是Χ上的两个L-半拓扑,若
是Χ上的两个L-半拓扑,若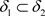 ,
,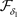 和
和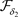 分别是关于
分别是关于 和
和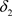 的全体闭集构成的集族,则
的全体闭集构成的集族,则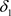 是比
是比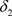 更粗的L-半拓扑当且仅当
更粗的L-半拓扑当且仅当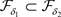 。
。
证明:(必要性)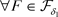 ,有
,有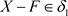 ,因
,因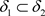 ,则
,则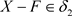 ,故
,故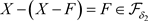 ,从而
,从而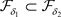 。
。
(充分性) 对于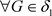 ,有
,有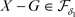 ,因
,因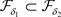 ,则
,则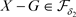 ,故
,故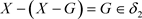 ,因此
,因此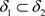 ,故
,故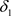 是比
是比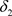 更粗的L-半拓扑。
更粗的L-半拓扑。
定理3.3 设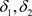 是Χ上的两个L-半拓扑,若
是Χ上的两个L-半拓扑,若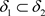 ,则
,则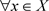 ,有
,有 。反之,结论不成立。
。反之,结论不成立。
证明:1) 设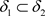 ,对于
,对于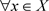 ,
,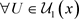 ,
,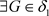 ,使得
,使得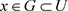 。因为
。因为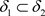 ,则
,则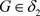 并且
并且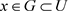 ,故
,故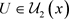 ,所以
,所以 。
。
2) 反之,可取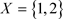 ,
,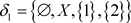 ,
,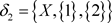 ,则
,则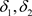 是Χ上的两个L-半拓扑,由L-半拓扑空间中邻域的定义有
是Χ上的两个L-半拓扑,由L-半拓扑空间中邻域的定义有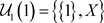 ,
,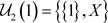 ,故
,故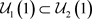 又
又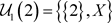 ,
,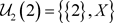 ,故
,故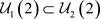 ,因此
,因此 ,但是
,但是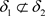 。
。
推论3.4 设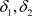 是Χ上的两个L-半拓扑,若
是Χ上的两个L-半拓扑,若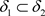 ,则
,则 ,有
,有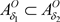 。反之,结论不成立。
。反之,结论不成立。
证明:1) ,
,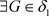 ,使得
,使得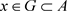 ,又
,又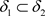 ,因此
,因此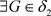 ,使得
,使得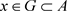 ,则
,则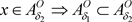 。
。
2) 反之可取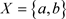 ,
,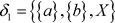 ,
,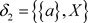 ,
, ,则
,则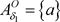 ,
,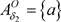 ,有
,有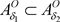 ,但
,但 ,故反之结论不成立。
,故反之结论不成立。
推论3.5 设 是Χ上的两个L-半拓扑,若
是Χ上的两个L-半拓扑,若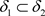 ,则
,则 ,有
,有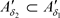 。反之,结论不成立。
。反之,结论不成立。
证明:1)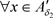 ,对于
,对于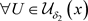 ,有
,有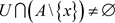 ,又
,又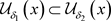 ,故
,故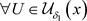 ,有
,有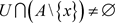 ,则
,则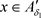 ,因此
,因此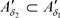 。
。
2) 反之可取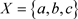 ,
,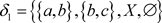 ,
,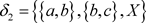 ,
,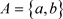 ,则
,则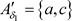 ,
,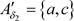 显然有
显然有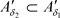 ,但
,但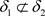 ,故反之结论不成立。
,故反之结论不成立。
推论3.6 设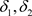 是Χ上的两个L-半拓扑,若
是Χ上的两个L-半拓扑,若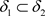 ,则
,则 ,有
,有 。反之,结论不成立。
。反之,结论不成立。
证明:由推论3.5可知若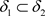 ,则有
,则有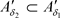 ,又
,又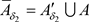 ,
,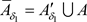 ,由此可得
,由此可得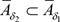 。
。
反之可取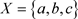 ,
,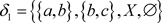 ,
,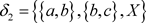 ,
,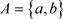 ,则
,则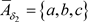 ,
,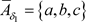 显然有
显然有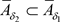 ,但
,但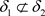 ,故反之结论不成立。
,故反之结论不成立。
4. 关于L-半拓扑基以及L-半拓扑基的一些性质
定义4.1 设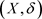 是L-半拓扑空间,
是L-半拓扑空间, ,如果
,如果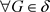 ,存在
,存在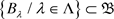 ,使得
,使得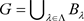 ,则称 为L-半拓扑
,则称 为L-半拓扑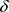 的一个基,
的一个基,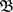 为Χ的一个L-拓扑基。
为Χ的一个L-拓扑基。
定理4.1 设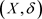 是一个L-半拓扑空间,
是一个L-半拓扑空间,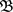 为L-半拓扑
为L-半拓扑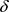 的一个基当且仅当
的一个基当且仅当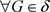 ,
, ,
,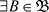 ,使得
,使得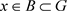 。
。
证明 (必要性) 设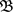 为
为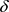 的一个基,即
的一个基,即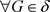 ,
, ,
,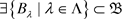 ,使得
,使得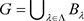 ,故
,故 ,
,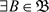 ,使得
,使得 。
。
(充分性)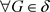 ,因为
,因为 ,
,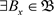 ,使得
,使得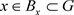 ,故
,故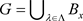 ,由定义可知
,由定义可知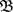 为
为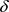 的一个基。
的一个基。
在一般拓扑空间中有:
定理4.2 [11] 设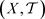 是一个拓扑空间,
是一个拓扑空间,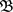 为
为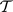 的一个基,则
的一个基,则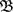 满足下面两个条件:(B1)
满足下面两个条件:(B1)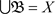 ;(B2)
;(B2)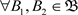 ,
,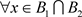 ,必
,必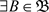 ,使得
,使得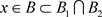 。
。
这两条性质在一般拓扑空间中成立,但在L-半拓扑空间中(B1)成立,(B2)不成立。
在L-半拓扑空间中,(B1)成立是不言而喻的。但是,(B2)是不成立的,下面举例子说明这个问题:
取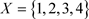 ,
,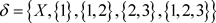 ,则
,则 ,存在
,存在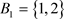 ,
,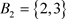 ,
,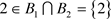 ,即不存在
,即不存在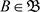 ,使得
,使得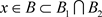 ,故(B2)不成立。
,故(B2)不成立。
5. 小结
本文首先引入L-半拓扑的概念,然后讨论了L-半拓扑空间的中点集理论、L-半拓扑子空间的性质、L-半拓扑基的性质以及L-半拓扑的比较,并且获得了一些相应的成果,从而,使L-半拓扑的基本性质得到推广。同时,也通过反例举出了在拓扑空间上成立而在L-半拓扑空间中不成立的一些结果。
文章引用
李 飞,朱培勇. 关于L-半拓扑空间上的一些探究
Some Research on L-Semi-Topology Space[J]. 理论数学, 2020, 10(04): 325-329. https://doi.org/10.12677/PM.2020.104041
参考文献
- 1. Csaszar, A. (2002) Generalized Topology, Generalized Continuity. Acta Mathematica Hungarica, 96, 351-357. https://doi.org/10.1023/A:1019713018007
- 2. Csaszar, A. (2005) Generalized Open Sets in Generalized Topologies. Acta Mathematica Hungarica, 106, 53-66. https://doi.org/10.1007/s10474-005-0005-5
- 3. Csaszar, A. (2009) Products of Generalized Topologies. Acta Mathematica Hungarica, 123, 127-132. https://doi.org/10.1007/s10474-008-8074-x
- 4. Csaszar, A. (2004) Separation Axioms for Generalized Topologies. Acta Mathematica Hungarica, 104, 63-69. https://doi.org/10.1023/B:AMHU.0000034362.97008.c6
- 5. Sarsak, M.S. (2011) Weak Separation Axioms in Generalized Topological Spaces. Acta Mathematica Hungarica, 131,110-121. https://doi.org/10.1007/s10474-010-0017-7
- 6. Shen, R. (2009) Remarks on Products of Generalized Topologies. Acta Mathematica Hungarica, 124, 363-369. https://doi.org/10.1007/s10474-009-8207-x
- 7. Min, W.K. (2010) Remarks on Separation Axioms on Generalized Topological Space. Chungcheong Mathematical Society, 23, 293-298.
- 8. Min, W.K. (2010) Generalized Continuous Functions Defined by Generalized Open Sets on Generalized Topological Spaces. Acta Mathematica Hungarica, 128, 299-306. https://doi.org/10.1007/s10474-009-9037-6
- 9. Min, W.K. (2009) Almost Continuity on Generalized Topologicalspace. Acta Mathematica Hungarica, 125, 121-125. https://doi.org/10.1007/s10474-009-8230-y
- 10. 胡西超, 朱培勇. 一类新型半拓扑空间及其分离性质[J]. 理论数学, 2015, 5(4): 129-135.
- 11. 朱培勇, 雷银彬. 拓扑学导论[M]. 北京: 科学出版社, 2009: 33-43.
- 12. 钟健, 陈道富, 朱培勇. 关于右半拓扑空间上的一些结果[J]. 理论数学, 2016, 6(3): 217-222.
- 13. 靳敏倩, 朱培勇. 关于R-半拓扑空间的一些探究[J]. 理论数学, 2016, 6(6): 459-463.
- 14. 宋颖潇, 丁猛, 朱培勇. 广义拓扑的比较[J]. 四川理工学院学报: 自然科学版, 2015, 28(4): 86-88.
- 15. 陈道富, 钟健, 朱培勇. 关于L-半拓扑空间的一些注记[J]. 理论数学, 2015, 5(6): 272-277.