Advances in Applied Mathematics
Vol.06 No.01(2017), Article ID:19638,12
pages
10.12677/AAM.2017.61010
The J-Selfadjoint Realizations of Two-Interval Forth-Order J-Symmetric Operators
Zhimin Zhang*, Meizhen Xu
College of Science, Inner Mongolia University of Technology, Hohhot Inner Mongolia

Received: Jan. 2nd, 2017; accepted: Jan. 21st, 2017; published: Jan. 24th, 2017
Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper we characterize all J-selfadjoint extensions for two-interval forth-order J-symmetric differential operators with regular or limit endpoints by the theory of the direct sum in Hilbert spaces.
Keywords:J-Symmetric Differential Operators, J-Selfadjoint Extensions, Regular Point, limit Point, Two-Interval

两区间四阶J-对称微分算子J-自伴扩张域的描述
张志敏*,许美珍
内蒙古工业大学理学院,内蒙古 呼和浩特

收稿日期:2017年1月2日;录用日期:2017年1月21日;发布日期:2017年1月24日

摘 要
本文利用Hilbert空间上的直和理论刻画了具有正则点和极限点的两区间四阶J-对称微分算子的所有J-自伴扩张。
关键词 :J-对称微分算子,J-自伴扩张,正则点,极限点,两区间

1. 引言
 -对称微分算子是一类特殊的有着重要应用背景的非对称微分算子,对此已经有了很多方面的研究(见 [1] - [9] )。在原子核物理、电磁场理论以及非均匀介质中的无线电波的传播等应用问题中,由微分算式所生成的
-对称微分算子是一类特殊的有着重要应用背景的非对称微分算子,对此已经有了很多方面的研究(见 [1] - [9] )。在原子核物理、电磁场理论以及非均匀介质中的无线电波的传播等应用问题中,由微分算式所生成的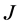 -自伴微分算子是很重要的一类算子。
-自伴微分算子是很重要的一类算子。
为了研究非对称算子的自伴扩张问题,Glazman [3] 最先从数学上提出了 -对称微分算子和
-对称微分算子和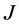 -自伴微分算子的概念。
-自伴微分算子的概念。
在Hilbert (简称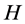 )空间中闭稠定算子称为
)空间中闭稠定算子称为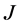 -对称的,如果对任何
-对称的,如果对任何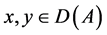 ,都有
,都有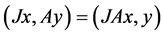 ,其中
,其中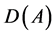 表示
表示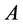 的定义域。如果
的定义域。如果 是
是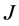 -对称的当且仅当
-对称的当且仅当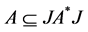 ,这里
,这里 是
是 的共轭算子。如果
的共轭算子。如果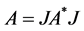 ,则称
,则称 是
是 -自伴的。
-自伴的。
Galindo [4] 和Knowles [5] 分别于1963年和1980年相继应用不同的方法给出了任何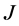 -对称微分算子都有
-对称微分算子都有 -自伴扩张的证明。
-自伴扩张的证明。
1959年,Zhikhar [6] 在 -对称微分算子正则域不空的情况下给出了它的部分特殊的(一端奇异)
-对称微分算子正则域不空的情况下给出了它的部分特殊的(一端奇异) 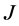 -自伴域的边界条件的描述。1981年,Knowles [1] 在正则域不空的情况下给出了
-自伴域的边界条件的描述。1981年,Knowles [1] 在正则域不空的情况下给出了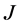 -对称微分算子的任一
-对称微分算子的任一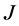 -自伴扩张域的边界条件的描述。但是判断一个算子正则域是否非空并不是一件容易的事,1985年,Race [2] 取消了正则域非空这一限制,得到了
-自伴扩张域的边界条件的描述。但是判断一个算子正则域是否非空并不是一件容易的事,1985年,Race [2] 取消了正则域非空这一限制,得到了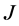 -对称微分算子的
-对称微分算子的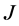 -自伴扩张的一般理论。1992年,刘景麟 [7] 又对这种
-自伴扩张的一般理论。1992年,刘景麟 [7] 又对这种 -自伴扩张的一般理论作了另一种完整的处理,得到
-自伴扩张的一般理论作了另一种完整的处理,得到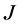 -自伴扩张域的一种抽象的边界条件的描述。
-自伴扩张域的一种抽象的边界条件的描述。
1988年,尚在久 [8] 应用Race的理论以及曹之江 [11] 和孙炯 [12] 的方法,取消了最小算子最小亏指数的限制,利用方程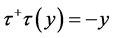 的解给出
的解给出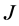 -自伴扩张域的边界条件的描述,这些边界条件不仅在正则点处有限制,而且在奇异点处也有限制。1996年,尚在久 [9] 给出了
-自伴扩张域的边界条件的描述,这些边界条件不仅在正则点处有限制,而且在奇异点处也有限制。1996年,尚在久 [9] 给出了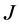 -对称微分算子
-对称微分算子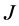 -自伴扩张的新描述,利用方程
-自伴扩张的新描述,利用方程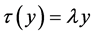 的解而不是更高阶方程
的解而不是更高阶方程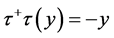 的解描述了
的解描述了 -对称微分算子的所有
-对称微分算子的所有 -自伴域在奇异端点的边条件,但其假设生成的最小算子具有非空正则域。
-自伴域在奇异端点的边条件,但其假设生成的最小算子具有非空正则域。
关于对称微分算子的自伴扩张不仅在一区间上有了很好的研究成果(见 [10] [11] [12] ),在两区间上也有了一系列的成果。自伴微分算子在两区间的研究最早在1986年由Everitt和Zettl在文 [13] 提出。2005年,Zettl [14] 用GKN理论从最大定义域中选出两组向量,根据亏指数的不同分别给出自伴域的刻画。2007年,王爱平、孙炯 [15] 用最大算子域中的实值向量给出了在带有适当乘数参数的Hilbert空间的直和框架下,二阶正则两区间实系数微分算子自伴域的描述。2007年,孙炯、王爱平 [16] 等人在一个带有适当乘数参数的Hilbert空间下,给出了两端奇异两区间二阶实系数微分算子的所有自伴扩张的描述。2012年,索建青 [17] 利用方程 的实参数解,先后描述了两区间一端正则一端奇异和两端奇异的自伴扩张。然而,两区间
的实参数解,先后描述了两区间一端正则一端奇异和两端奇异的自伴扩张。然而,两区间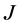 -自伴扩张的研究成果甚少。由于
-自伴扩张的研究成果甚少。由于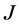 -对称微分算子的
-对称微分算子的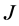 -自伴扩张与对称微分算子的自伴扩张有很大的相似之处,因此,我们将自伴的两区间理论推广到
-自伴扩张与对称微分算子的自伴扩张有很大的相似之处,因此,我们将自伴的两区间理论推广到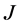 -自伴的两区间理论。
-自伴的两区间理论。
本文给出四阶微分算式生成的最小算子在两区间上所有的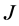 -自伴扩张域的特征,其中只考虑区间端点为正则点或极限点的情形。对于两区间而言,实际上我们有两个
-自伴扩张域的特征,其中只考虑区间端点为正则点或极限点的情形。对于两区间而言,实际上我们有两个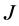 -对称微分算子:
-对称微分算子: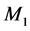 定义在区间
定义在区间 上,
上,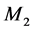 定义在区间
定义在区间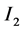 上。一般的,区间
上。一般的,区间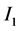 的右端点和区间
的右端点和区间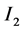 的左端点是否相同已不在重要,区间
的左端点是否相同已不在重要,区间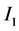 和区间
和区间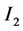 是任意的两个区间,他们可能是相同的,重合的或者完全不相交的。特别的,我们定义两个微分算式生成的相应的最小算子和最大算子,并利用边界条件描述最小算子所有的
是任意的两个区间,他们可能是相同的,重合的或者完全不相交的。特别的,我们定义两个微分算式生成的相应的最小算子和最大算子,并利用边界条件描述最小算子所有的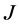 -自伴扩张域。
-自伴扩张域。
2. 预备知识
引理 2.1 [2] 每个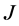 -对称算子都有一个
-对称算子都有一个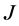 -自伴延拓。
-自伴延拓。
引理 2.2 [2] 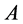 是一个
是一个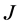 -对称算子,
-对称算子, 是
是 的
的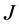 -对称扩张,如果
-对称扩张,如果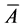 是
是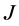 -自伴算子,当且仅当
-自伴算子,当且仅当 是最大的
是最大的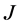 -对称算子。
-对称算子。
引理 2.3 [2] (1)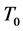 是闭稠定的
是闭稠定的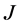 -对称微分算子,且
-对称微分算子,且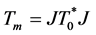 ;
;
(2) 对任何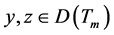 ,极限
,极限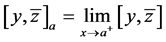 和
和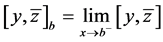 都存在,且
都存在,且
 , (1)
, (1)
这里,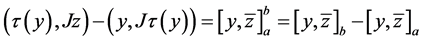 ;
;
(3)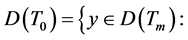 对任何
对任何 。若
。若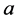 是正则的,
是正则的,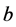 是奇异的,则
是奇异的,则
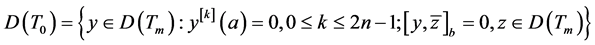 。 (2)
。 (2)
引理 2.4 [2] (Lagrange恒等式) 对一切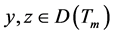 ,
,
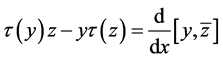 , (3)
, (3)
其中,
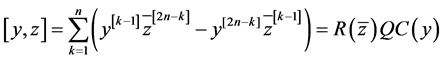 , (4)
, (4)
称为Lagrange双线性型。其中 ,
, ,且
,且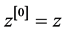 ,
, ,
,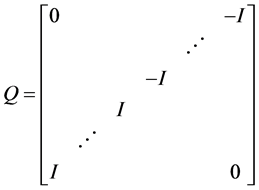 ,其中,I是单位矩阵,且Q有性质
,其中,I是单位矩阵,且Q有性质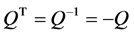 。
。
引理 2.5 [1] (Naimark补缀定理) 假定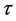 在区间
在区间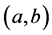 是正则的,令
是正则的,令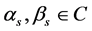 ,
,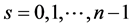 。则存在函数
。则存在函数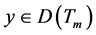 使得
使得
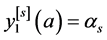 ,
,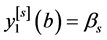
 ,
, 。
。
引理 2.6 [2] 设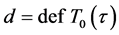 ,则
,则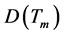 中的线性流形
中的线性流形 是
是 的
的 -自伴扩张域的充要条件是存在函数
-自伴扩张域的充要条件是存在函数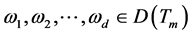 ,使得
,使得
(a)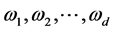 模
模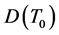 线性无关;
线性无关;
(b)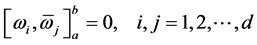 ;
;
(c)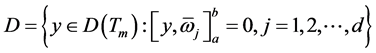 。
。
定理 2.7 [2] 对于任意的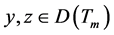 ,如果
,如果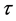 在点
在点 是正则的,点
是正则的,点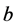 是极限点型的,且
是极限点型的,且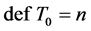 ,则有
,则有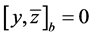 。因此,在引理2.6的条件(b),(c)中,
。因此,在引理2.6的条件(b),(c)中,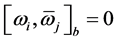 ,
,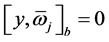 。
。
3. 主要结论及证明
令 ,
,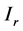 表示以
表示以 为左端点
为左端点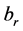 为右端点的区间,即
为右端点的区间,即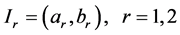 。设四阶微分算式
。设四阶微分算式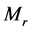 为
为
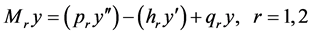 。 (5)
。 (5)
函数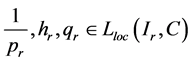 。
。
定义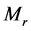 在
在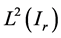 生成的最大算子
生成的最大算子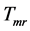 ,其定义域为
,其定义域为
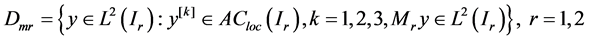 。
。
定义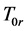 为微分算式
为微分算式 在
在 生成的最小算子。
生成的最小算子。
设
 ,
,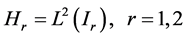 。 (6)
。 (6)
两区间最大、最小算子域及最大、最小算子是每个区间上相应算子域和算子的直和,即
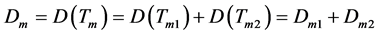 , (7)
, (7)
 。 (8)
。 (8)
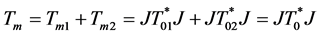 , (9)
, (9)
 。 (10)
。 (10)
令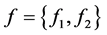 ,
,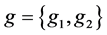 表示空间
表示空间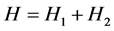 中的元素,其中
中的元素,其中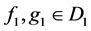 ,
,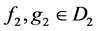 。则
。则
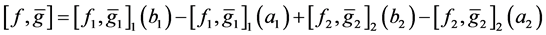 。 (11)
。 (11)
如果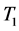 是
是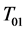 的
的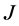 -自伴扩张,
-自伴扩张,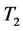 是
是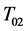 的
的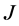 -自伴扩张,则
-自伴扩张,则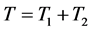 是
是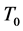 的
的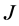 -自伴扩张。
-自伴扩张。
引理 3.1 [12] 定义在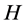 中的最小算子
中的最小算子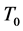 是稠定的闭的
是稠定的闭的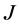 -对称微分算子,其亏指数
-对称微分算子,其亏指数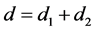 。其中,
。其中,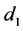 是
是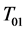 在空间
在空间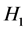 的亏指数,
的亏指数,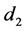 是
是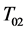 在空间
在空间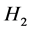 的亏指数。
的亏指数。
引理3.2 [1] (Naimark补缀定理) 假定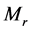 在
在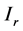 上是正则的,
上是正则的,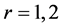 。令
。令 ,
, 。则存在函数
。则存在函数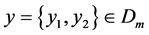 使得
使得
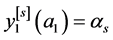 ,
,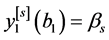 ,
,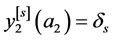 ,
,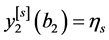 ,
, 。
。
定理 3.3 令 ,
,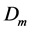 中线性流形
中线性流形 是最小算子
是最小算子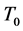 的
的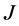 -自伴扩张域当且仅当存在函数
-自伴扩张域当且仅当存在函数 满足
满足
(i) 模
模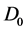 线性无关;
线性无关;
(ii)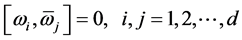 ;
;
(iii) 。
。
证明 这个结果是本文的基础,定理的证明与 [2] 的定理4.7相似,因此省略。
定理 3.4 设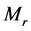 在端点
在端点 是正则的,且
是正则的,且 ,那么
,那么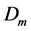 中的线性流形
中的线性流形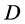 是
是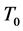 的
的 -自伴扩张域的充要条件是存在四个
-自伴扩张域的充要条件是存在四个 阶矩阵
阶矩阵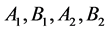 满足
满足
(a) ;
;
(b)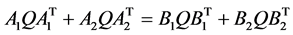 ;
;
(c)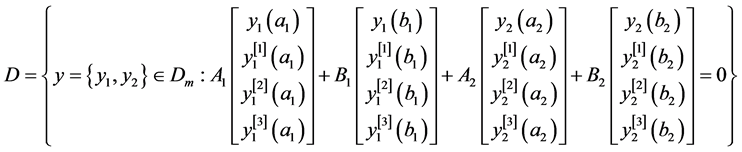 。
。
证明 必要性。设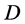 是最小算子
是最小算子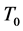 的
的 -自伴扩张域。由定理3.3知,存在
-自伴扩张域。由定理3.3知,存在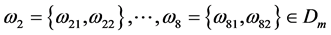
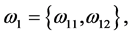 满足定理3.3的条件(i),(ii),(iii)。由(4)有
满足定理3.3的条件(i),(ii),(iii)。由(4)有
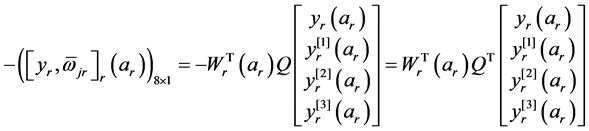 ,
,
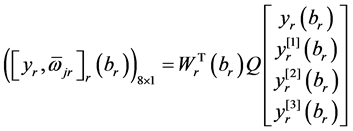 ,
,
这里
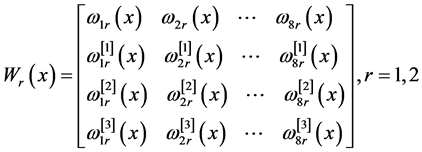 。
。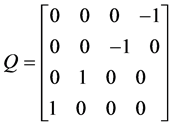 。
。
令
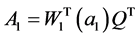 ,
,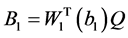 ,
,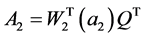 ,
,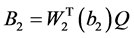 。
。
因此条件(iii)等价于定理3.4的条件(c)。
下面证明矩阵 满足定理3.4的条件(a)与(b)。
满足定理3.4的条件(a)与(b)。
显然 。若
。若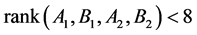 ,则存在不全为零的数
,则存在不全为零的数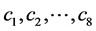 使得
使得
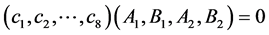 。 (12)
。 (12)
因此
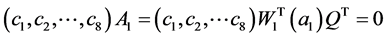 ,
,
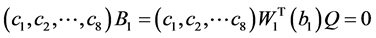 ,
,
同理
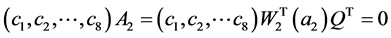 ,
,
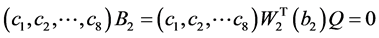 。
。
由于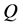 是非奇异的,有
是非奇异的,有
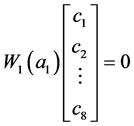 ,
,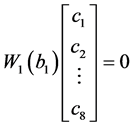 ,
,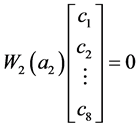 ,
, 。
。
令 ,即,
,即,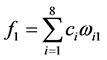 ,
, ,则
,则
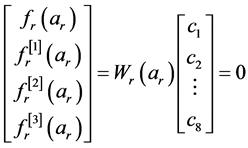 ,
,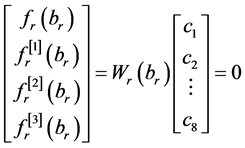 , (13)
, (13)
故由(13)与(2)有 ,
, ,所以
,所以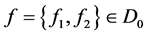 ,这与
,这与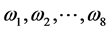 模
模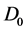 线性无关矛盾。
线性无关矛盾。
下面证明(b)。由(4),有
 ,
,
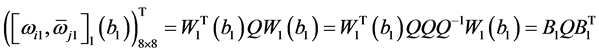 ,
,
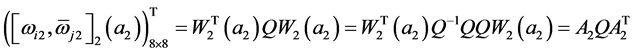 ,
,
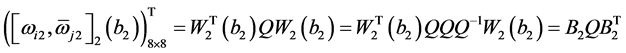 ,
,
 。因此定理3.3的条件(ii)等价于
。因此定理3.3的条件(ii)等价于
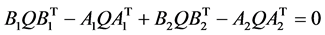 ,即
,即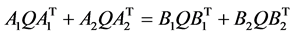 。
。
充分性。设矩阵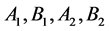 满足条件(a)与(b)。下面证明由(c)定义的
满足条件(a)与(b)。下面证明由(c)定义的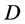 是
是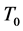 的
的 -自伴扩张域。
-自伴扩张域。
令
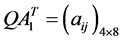 ,
,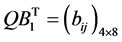 ,
, ,
, 。 (14)
。 (14)
由引理3.2,选择函数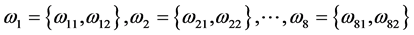 属于
属于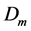 使得
使得
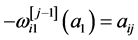 ,
,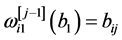 ,
,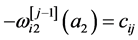 ,
,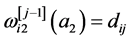 ,(15)
,(15)
其中,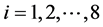 ,
,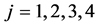 。
。
由(14)与(4),有
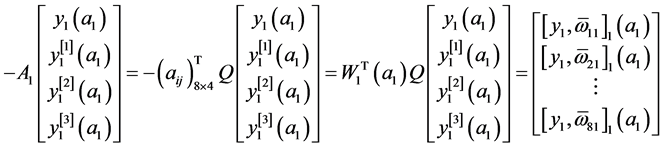 ,
,
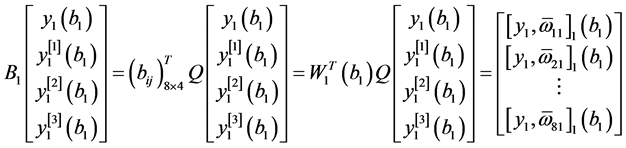
 ,
,
同理
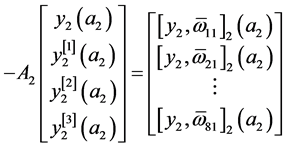 ,
,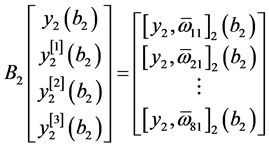 。
。
故条件(c)转化为边界条件(iii),即
 ,
,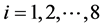 。
。
最后证明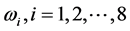 满足定理3.3的条件(i)与(ii)。
满足定理3.3的条件(i)与(ii)。
用反证法证明条件(i)成立。如若不然,那么存在不全为零的数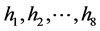 使得
使得
 ,即
,即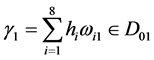 ,
,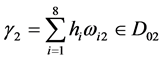 。
。
因此
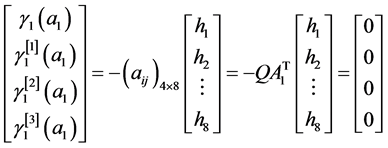 ,
,
则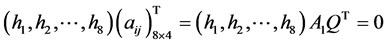 ,由于
,由于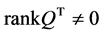 ,于是
,于是
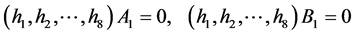 ,
,
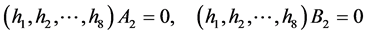 。
。
所以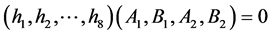 ,这与
,这与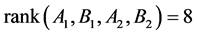 矛盾。
矛盾。
下面证明条件(ii)成立。由(14)和(15)有
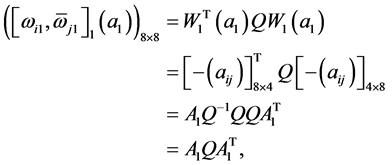
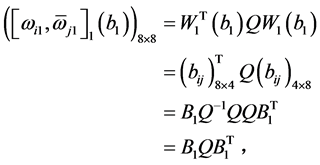
同理
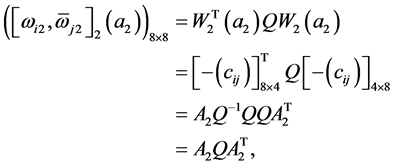
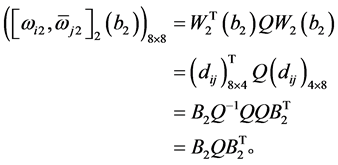
所以,由条件(b)得
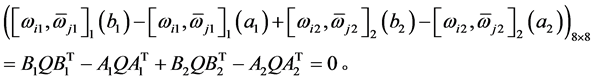
于是由定理3.3得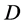 是
是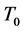 的
的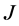 -自伴扩张域。
-自伴扩张域。
定理3.4给出了最小算子的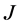 -自伴扩张域边界条件耦合的情况,其条件(c)等价于
-自伴扩张域边界条件耦合的情况,其条件(c)等价于
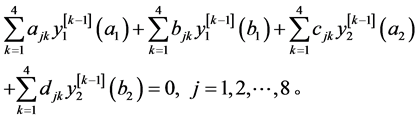 (16)
(16)
条件(b)等价于
 (17)
(17)
区间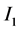 和
和 可以有不同的关系,如相同、重合、分离;于是,考虑区间四个端点的关系,讨论如下
可以有不同的关系,如相同、重合、分离;于是,考虑区间四个端点的关系,讨论如下
(1) 区间四个端点中任意一个点与其他三个点分离,此时区间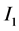 和
和 是不分离的假设
是不分离的假设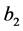 点被分离,选择
点被分离,选择
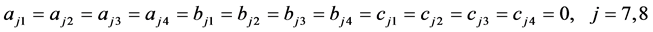 ;
;
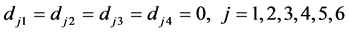 。
。
则边界条件(16)转化为
 ,(18)
,(18)
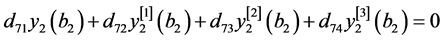 , (19)
, (19)
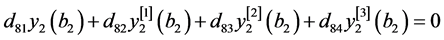 。 (20)
。 (20)
判定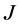 -自伴性的边界条件(17)转化为
-自伴性的边界条件(17)转化为
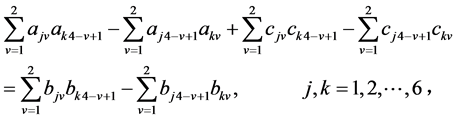 (21)
(21)
 。 (22)
。 (22)
(2) 区间四个端点中任意两个点分离。
(i) 区间 和
和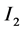 是不分离的。假设
是不分离的。假设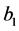 与
与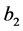 是分离的,选择
是分离的,选择
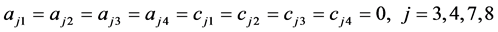 ;
;
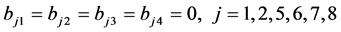 ;
;
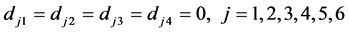 。
。
边界条件(16)转化为(19)和(20)以及
 , (23)
, (23)
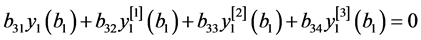 , (24)
, (24)
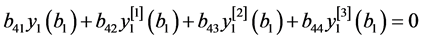 。 (25)
。 (25)
判定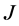 -自伴性的边界条件(17)转化为(22)以及
-自伴性的边界条件(17)转化为(22)以及
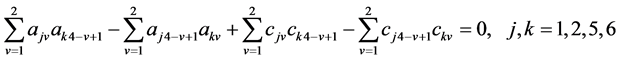 , (26)
, (26)
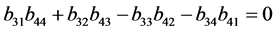 。 (27)
。 (27)
(ii) 区间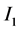 和
和 是分离的。假设
是分离的。假设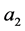 与
与 是分离的,选择
是分离的,选择
 ;
;
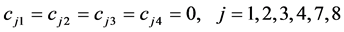 ;
;
 。
。
边界条件(16)转化为(19)和(20)以及
 , (28)
, (28)
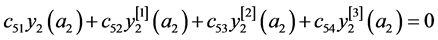 , (29)
, (29)
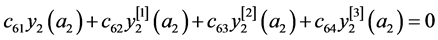 。 (30)
。 (30)
判定 -自伴性的边界条件(17)转化为(22)以及
-自伴性的边界条件(17)转化为(22)以及
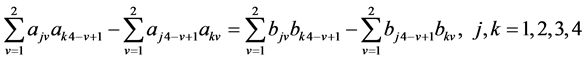 , (31)
, (31)
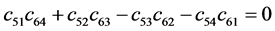 。 (32)
。 (32)
(3) 区间四个端点都是分离的,此时区间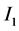 和
和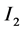 是分离的。选择
是分离的。选择
 ;
;
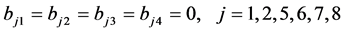 ;
;
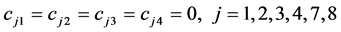 ;
;
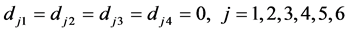 。
。
边界条件(16)转化为(19),(20),(24),(25)和(29),(30)以及
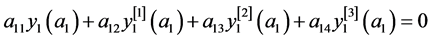 ,(33)
,(33)
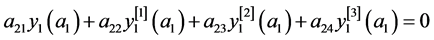 。 (34)
。 (34)
判定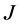 -自伴性的边界条件(17)转化为(22),(27)和(32)以及
-自伴性的边界条件(17)转化为(22),(27)和(32)以及
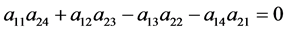 。 (35)
。 (35)
(4) 区间四个端点中任意两个点耦合,另外两个点也是耦合的。
(i) 区间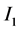 和
和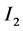 是不分离的。假设
是不分离的。假设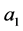 与
与 是耦合的,
是耦合的, 与
与 是耦合的,选择
是耦合的,选择
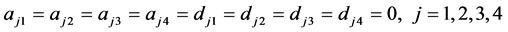 ;
;
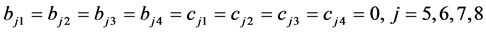 。
。
边界条件(16)转化为
 , (36)
, (36)
 。 (37)
。 (37)
判定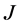 -自伴性的边界条件(17)转化为
-自伴性的边界条件(17)转化为
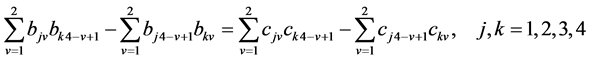 , (38)
, (38)
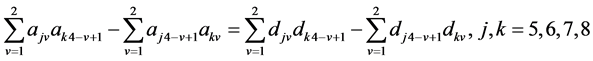 。(39)
。(39)
(ii) 区间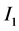 和
和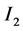 是分离的。假设
是分离的。假设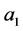 与
与 是耦合的,
是耦合的,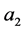 与
与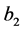 是耦合的,选择
是耦合的,选择
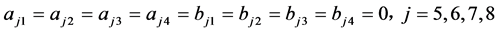 ;
;
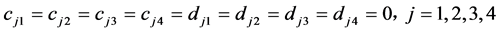 。
。
边界条件(16)转化为(28)以及
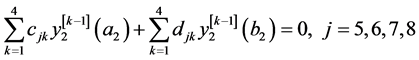 。 (40)
。 (40)
判定 -自伴性的边界条件(17)转化为(31)以及
-自伴性的边界条件(17)转化为(31)以及
 。 (41)
。 (41)
定理3.4给出了亏指数为8的最小算子的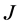 -自伴扩张域的描述,并讨论了
-自伴扩张域的描述,并讨论了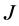 -自伴算子边界条件分离与耦合的情形。根据两区间正则点和极限点的个数可将最小算子
-自伴算子边界条件分离与耦合的情形。根据两区间正则点和极限点的个数可将最小算子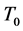 的亏指数取0,2,4,6。并可根据亏指数的不同,在正则情况下分析
的亏指数取0,2,4,6。并可根据亏指数的不同,在正则情况下分析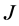 -自伴算子边界条件分离与耦合的情况。讨论如下
-自伴算子边界条件分离与耦合的情况。讨论如下
1. 当区间四个端点都为极限点时,最小算子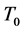 的亏指数
的亏指数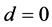 ,此时
,此时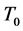 是本身的
是本身的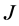 -自伴扩张。
-自伴扩张。
2. 当区间端点有三个点是极限点,一个点是正则点时,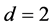 。此时归纳为一区间的
。此时归纳为一区间的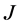 -自伴扩张域的描述,边界条件只在正则点处有限制。假设
-自伴扩张域的描述,边界条件只在正则点处有限制。假设 是正则点,其他情形和这种完全类似。
是正则点,其他情形和这种完全类似。
设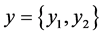 ,
, ,
, 。于是定理3.3可归纳为
。于是定理3.3可归纳为
(a)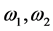 模
模 线性无关;
线性无关;
(b)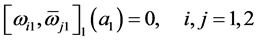 ;
;
(c)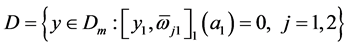 。
。
3. 当区间端点有两个点是极限点,两个点是正则点时,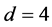 。这时有以下两种情况
。这时有以下两种情况
(1) 两个正则点在同一个区间上,故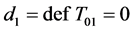 ,
,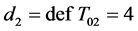 。假设
。假设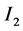 是正则区间,
是正则区间, 为
为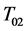 的
的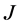 -自伴扩张,则最小算子
-自伴扩张,则最小算子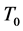 在两区间的
在两区间的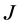 -自伴扩张为
-自伴扩张为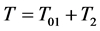 。
。
(2) 两个正则点不在同一个区间上,故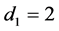 ,
,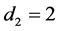 。假设
。假设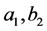 是极限点,
是极限点,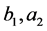 是正则点。其他情形和这种完全类似。
是正则点。其他情形和这种完全类似。
设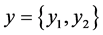 ,
,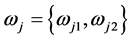 ,
,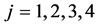 。于是定理3.3可归纳为
。于是定理3.3可归纳为
(a)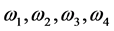 模
模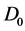 线性无关;
线性无关;
(b)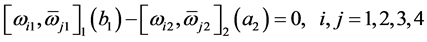 ;
;
(c) 。
。
因此,条件(c)就等价于(36)的四个等式,条件(b)就等价于(38)的六个等式,条件(a)说明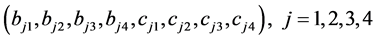 线性无关。
线性无关。
4. 当区间端点有一个点是极限点,三个点是正则点时, 。那么一个区间的两个端点都为正则点,另一个区间一个端点为正则点一个端点为极限点。假设
。那么一个区间的两个端点都为正则点,另一个区间一个端点为正则点一个端点为极限点。假设 是正则点,
是正则点,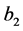 是极限点,所以,
是极限点,所以,
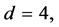 。其他情形和这种完全类似。
。其他情形和这种完全类似。
设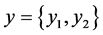 ,
,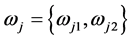 ,
, 。于是定理3.3可归纳为
。于是定理3.3可归纳为
(a)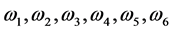 模
模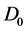 线性无关;
线性无关;
(b)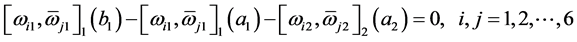 ;
;
(c)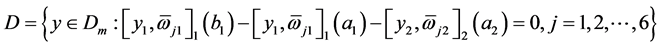 。
。
因此,条件(c)就等价于等式(18),条件(b)等价于(21),条件(a)说明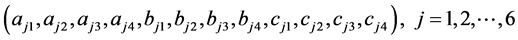 线性无关。
线性无关。
等式(18)描述了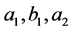 点边界条件耦合的情形,但边界条件在区间
点边界条件耦合的情形,但边界条件在区间 和
和 可能是分离的,也可能是不分离的。
可能是分离的,也可能是不分离的。
(1) 区间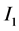 和
和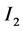 是分离的,选择
是分离的,选择
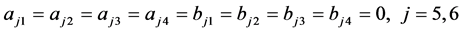 ;
;
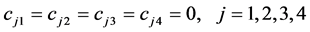 。
。
(18)的六个边界条件转化为(28)-(30),判定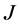 -自伴性的边界条件(21)转化为(31)和(32)。这种情形讨论了边界条件在
-自伴性的边界条件(21)转化为(31)和(32)。这种情形讨论了边界条件在 点和
点和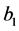 点耦合与
点耦合与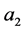 点分离的情况,还有一种比较特殊的情形,即边界条件在三个点是分离的。令
点分离的情况,还有一种比较特殊的情形,即边界条件在三个点是分离的。令
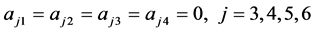 ;
;
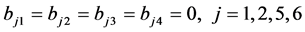 ;
;
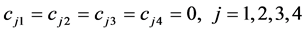 。
。
(18)的六个边界条件转化为(24),(25),(29),(30),(33)和(34),判定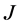 -自伴性的边界条件(21)转化为(27),(32)和(35)。
-自伴性的边界条件(21)转化为(27),(32)和(35)。
(2) 区间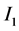 和
和 是不分离的,选择
是不分离的,选择
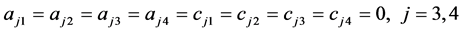 ;
;
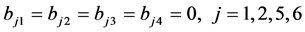 。
。
(18)的六个边界条件转化为(23)~(25),判定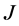 -自伴性的边界条件(21)转化为(26)和(27)。
-自伴性的边界条件(21)转化为(26)和(27)。
基金项目
国家自然科学基金(11361039, 11561051);国家青年基金(11301259)。
文章引用
张志敏,许美珍. 两区间四阶J-对称微分算子J-自伴扩张域的描述
The J-Selfadjoint Realizations of Two-Interval Forth-Order J-Symmetric Operators[J]. 应用数学进展, 2017, 06(01): 78-89. http://dx.doi.org/10.12677/AAM.2017.61010
参考文献 (References)
- 1. Knowles, I. (1981) On the Boundary Conditions Characterizing J-Selfadjoint Extensions of J-Symmetric Operators. Journal of Dif-ferential Equations, 40, 193-216. https://doi.org/10.1016/0022-0396(81)90018-8
- 2. Race, D. (1985) The Theory of J-Selfadjoint Extensions of J-Symmetric Operators. Journal of Differential Equations, 57, 258-274. https://doi.org/10.1016/0022-0396(85)90080-4
- 3. Glazman, I.M. (1957) An Analogue of the Extension Theory of Hermitian Operators and a Non-Symmetric One-Dimensional Boundary Problem on a Half-Axis. Doklady Akademii Nauk SSSR, 115, 214-216.
- 4. Galindo, A. (1962) On the Existence of J-Selfadjoint Extensions of J-Symmetric Operators with Adjoint. Communi-cations on Pure and Applied Mathematics, 15, 423-425. https://doi.org/10.1002/cpa.3160150405
- 5. Knowles, I. (1980) On J-Selfadjoint Extensions of J-Symmetric Operators. Proceedings of the American Mathematical Society, 79, 42-44. https://doi.org/10.2307/2042383
- 6. Zhikhar, N.A. (1959) The Theory of Extensions of J-Symmetric Operators. Ukrains' kyi Matematychnyi Zhurnal, 11, 352-364.
- 7. 刘景麟. 关于J-对称算子的自伴延拓[J]. 内蒙古大学学报(自然科学版), 1992, 23(3): 312-316.
- 8. Shang, Z. (1988) On J-Selfadjoint Extensions of J-Symmetric Ordinary Differential Operators. Journal of Differential Equations, 73, 153-177. https://doi.org/10.1016/0022-0396(88)90123-4
- 9. 尚在久. 关于J-对称微分算子的J-自伴扩张的若干注记[J]. 数学学报, 1996, 39(3): 387-395.
- 10. Naimark, M.A. (1954) Linear Differential Operators. GITTI, Moscow.
- 11. Cao, Z. (1985) On Self-Adjoint Extensions of n-th Order Differential Operators in the Limit Circle Case. Acta Mathematocs Sinica, 28, 205-217.
- 12. Sun, J. (1986) On the Self-Adjoint Extensions of Symmetric Ordinary Differential Operators with Middle Deficiency Indices. Acta Mathematica Sinica, 2, 152-167. https://doi.org/10.1007/BF02564877
- 13. Everitt, W.N. and Zettl, A. (1986) Sturm-Liouville Differential Operators in Direct Sum Spaces. Rocky Mountain Journal of Mathematics, 16, 497-516. https://doi.org/10.1216/RMJ-1986-16-3-497
- 14. Zettl, A. (2005) Sturm-Liouville Theory. American Mathematical Socie-ty.
- 15. Wang, A., Sun, J. and Zettl, A. (2007) Two-Interval Sturm-Liouville Operators in Modified Hilbert Spaces. Journal of Ma-thematical Analysis and Applications, 328, 390-399. https://doi.org/10.1016/j.jmaa.2006.05.058
- 16. Sun, J., Wang, A. and Zettl, A. (2007) Two-Interval Sturm-Liouville Operators in Direct Sum Spaces with Inner Product Multiples. Results in Mathematics, 50, 155-168. https://doi.org/10.1007/s00025-006-0241-1
- 17. Suo, J. and Wang, W. (2012) Two-Interval Even Order Differential Operators in Direct Sum Spaces. Results in Mathematics, 62, 13-32. https://doi.org/10.1007/s00025-011-0126-9
*通讯作者。