Advances in Applied Mathematics
Vol.06 No.07(2017), Article ID:22548,11
pages
10.12677/AAM.2017.67106
The Research of Denoising Method Based on Empirical Mode Decomposition Theory
Shuwen Niu
School of Mathematics and Physics, China University of Geosciences, Wuhan Hubei
Received: Oct. 9th, 2017; accepted: Oct. 23rd, 2017; published: Oct. 31st, 2017

ABSTRACT
Based on the basic idea of empirical mode decomposition method, this paper presents a new filtering method by using the significant differences between the noise curvature curve and the discrete Frechet distance of the signal curvature curve. Using this method to analyze the simulation data, the results show that the new filtering method is an effective denoising method. Compared with the traditional empirical mode decomposition (EMD) method, this method can denoise the signal and have high signal to noise ratio. This method can effectively reduce the influence of noise on the signal, then extract useful information from the noisy signal.
Keywords:Empirical Mode Decomposition, Curvature, Discrete Frechet Distance, Signal Denoising
基于经验模态分解理论的去噪方法研究
牛淑文
中国地质大学数学与物理学院,湖北 武汉
收稿日期:2017年10月9日;录用日期:2017年10月23日;发布日期:2017年10月31日

摘 要
基于经验模态分解方法的基本思想,本文利用噪声曲率曲线与信号曲率曲线的离散Frechet距离有显著差异这一特性,提出了一种新的滤波法。采用该方法对模拟数据进行分析,结果表明新的滤波法是一种有效的去噪方法,与传统的经验模态分解(Empirical Mode Decomposition, EMD)方法相比,该方法能够实现对信号的去噪,具有较高的信噪比。该方法可有效地削弱噪声对信号的影响,进而从含噪信号中提取出有用信息。
关键词 :经验模态分解,曲率,离散Frechet距离,信号去噪

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
目前常用的去噪方法只适用于分析线性、平稳的时间序列。为了克服这些方法的局限性,可以利用小波变换域系数进行去噪 [1] [2] 。由于小波方法的基函数是固定的,所以,该方法具有非自适应性,一旦确定好小波基,它将被用于分析所有数据。美国工程院院士黄锷博士于1998年提出了研究非线性非平稳信号的经验模态分解(Empirical Mode Decomposition, EMD)方法 [3] 。该方法依据输入信号自身的特点,无须预先设定任何基函数,可以自适应地将信号分解成若干个本征模态函数,是一种自适应的数据处理或挖掘方法。但是,当信号的时间尺度存在跳跃性变化或中断时,对信号进行EMD分解,会出现模态混叠的现象。为了更好地解决模态混叠问题,Z. Wu和N. E. Huang在2009年提出了总体经验模式分解(Ensemble Empirical Mode Decomposition, EEMD)方法 [4] ,这是一种噪声辅助的数据分析方法(Noise Assisted Data Analysis, NADA)。由于平均次数的限制,该方法中添加的白噪声并没有被完全中和。因此,为了减小由白噪声引起的重构误差,文献 [5] 提出了互补集合经验模态分解(Complementary Ensemble Empirical Mode Decomposition, CEEMD)方法。CEEMD方法很大程度上减少了重建信号中的残余噪声,但如果参数选择不合适,会出现伪分量,导致最后获得的本征模态函数(Intrinsic Mode Function,IMF)不能真正满足IMF的定义条件。为了克服这个问题,文献 [6] 提出了自适应噪声的总体集合经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise, CEEMDAN)方法。基于CEEMDAN方法,文献 [7] 提出了改进的自适应噪声总体集合经验模态分解(Improved CEEMDAN, ICEEMDAN)方法。本文采用该方法来获得准确的原始信号重构,以期达到对GPS时间序列去除观测噪声的目的。
2. EMD及其改进方法
2.1. EMD以及相关方法
EMD方法依据输入信号自身的特点,自适应地将信号分解成若干个本征模态函数(intrinsic mode function, IMF)之和。每个IMF分量必须满足以下两个条件:1) 在整个时间范围内,局部极值点和过零点的数目必须相等,或最多相差一个;2) 在任意时刻点,局部最大值的包络(上包络线)和局部最小值的包络(下包络线)的平均值必须为零 [5] 。
EMD方法实际上是一种循环迭代算法,该算法的具体过程如下:
1) 分别找出原数据序列 所有的极大值点和极小值点,并用三次样条插值函数拟合形成原数据的上包络线和下包络线。
2) 计算上包络线和下包络线的均值,记作 ,用原数据序列 减去该均值,即可得到一个去掉低频的新数据序列 :
3) 由原数据序列减去均值后得到的新数据序列 ,若满足IMF的条件,则作为第一个IMF分量序列,否则,需要对它重复进行上述处理过程。重复进行上述处理过程k次后,直到 符合IMF的定义要求,所得到的均值趋于零为止,这样就得到了第1个IMF分量 ,它代表信号 中最高频率的分量:
4) 将 从 中分离出来,即得到一个去掉高频分量的差值信号 ,即有:
将 作为原始数据,重复步骤(1)~(3),即可得到第二个IMF分量 ,重复n次,得到n个IMF分量,则有:
当 满足给定的终止条件(通常使 成为一个单调函数)时,循环结束。原始信号 经过n次分解后可以写成以下表达式:
其中, 为残余分量,代表信号的平均趋势,而 分别为包含了信号不同频率的IMF分量。
EEMD方法、CEEMD方法以及CEEMDAN方法如图1所示。
2.2. ICEEMDAN方法
为了减少模态中所包含的噪声总量,文献 [7] 进一步提出了ICEEMDAN方法,该方法能够避免杂散模态的产生。定义 为由EMD分解产生的第j个模态分量, 为信号的局部均值。该算法的具体分解过程如下:
1) 对信号 进行I次EMD分解,计算出局部均值,得到第一个剩余分量,即 。其中, 。
2) 当 时,计算出第一个固有模态分量为 。

Figure 1. EMD and related methods
图1. EMD以及相关方法
3) 对信号 进行I次EMD分解,计算出局部均值,得到第二个剩余分量,即 。则第二个固有模态分量为
4) 计算出第k个剩余分量和第k个固有模态分量 :
5) 重复步骤(4),计算出下一个k。直到获得的残余分量不能被EMD进一步分解,即残余分量为一个单调函数为止。
3. 基于曲率–离散Frechet距离的重构分量选择
3.1. 曲线的曲率
曲率是指在一条曲线或不同曲线上不同点的弯曲程度 [8] 。曲率的倒数就是曲率半径,即 。设曲线方程为 ,且 具有二阶导数,则曲率k为:
(1)
3.2. Frechet距离
Frechet距离(Frechet Distance, FD) [9] 是法国数学家Maurice Rene Frechet在1906年提出的一种空间路径的相似性描述,指利用两个目标的路径以及两条曲线上所有离散点的距离,量化两条曲线的相似度。这种方法直观,而且与Hausdorff距离等其他相似度量化方法相比,其可以更好地刻画折线曲线的相似度。设定t是时间点,该时刻,曲线a上的采样点为 ,曲线B上采样点为 。如果使用欧氏距离,则容易定义 。在每次采样中t离散的遍历区间 ,得到该种采样下的最大距离 。Frechet距离就是使该最大距离最小化的采样方式下的值。在离散方式下,我们不可能得到真实的Frechet距离,而可以无限的趋近。离散Frechet距离 定义为:
(2)
3.3. 重构分量的选择
对于信号 , 为原信号, 为噪声信号。信号 可以被分解为n个本征模态分量 和一个残余分量,所有的本征模态分量按照从高频到低频依次排列。一般情况下,前几个IMF分量为噪声,后几个IMF为原信号,因此信号 可以表示为:
(3)
由于所有的本征模态分量都有它固有的特性,所以每个本征模态分量的曲线曲率均不相同。为了简化,将本征模态分量的曲率记为Cur_IMFs。原信号的曲率波形与信号 的曲率波形相似,而噪声信号的曲率波形与信号 的曲率波形不同。因此,可以通过本征模态分量的曲率波形的突变来区分噪声信号和原信号。计算出各个本征模态分量的曲率曲线与信号 曲率曲线的离散Frechet距离,则可以找出重构分量的模态序号k值。具体步骤如下:
1) 运用EMD、EEMD、CEEMD、CEEMDAN和ICEEMDAN 5种方法分解信号 ,得到本征模态分量。
2) 分别计算出信号 和每个本征模态分量的曲率。
3) 计算信号 的曲率和每个本征模态分量曲率之间的离散Frechet距离。
4) 取离散Frechet距离的最小值所对应的本征模态分量的序号为k值。
5) 信号 可以重构为:
(4)
4. 仿真实验
为了比较EMD、EEMD、CEEMD、CEEMDAN和ICEEMDAN 5种方法的分解效果,不失一般性地,考察仿真信号 ,通过公式(5)模拟了5年的坐标序列。图2所示为原信号和原信号的曲率,图3为含噪信号。
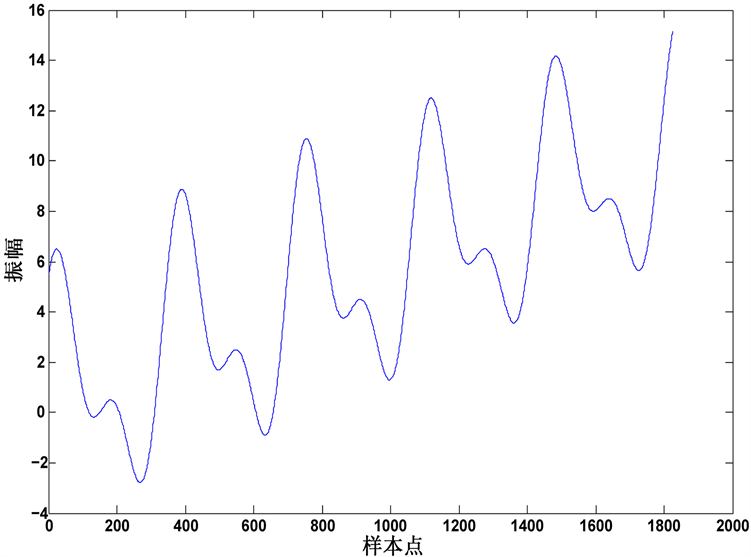

Figure 2. Signal and curvature
图2. 信号和曲率
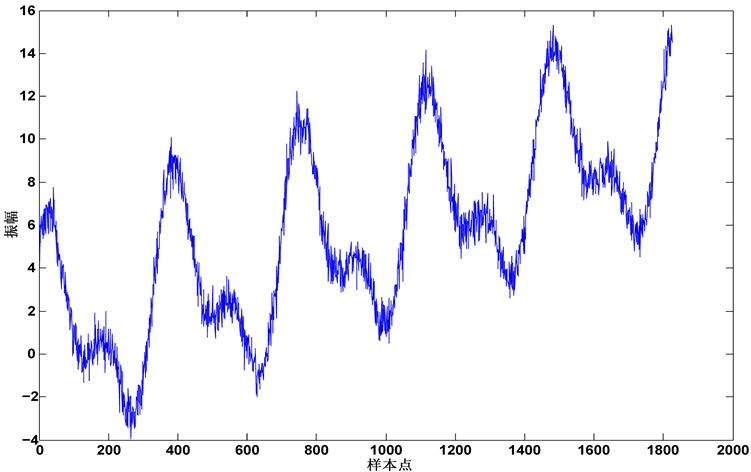
Figure 3. Noisy signal waveform
图3. 含噪信号波形
(5)
其中, 时变信号的模拟数据,数据长度为1825; , , , , , ; 是GPS年积日格式的时间; 是信噪比为5 dB的高斯白噪声; 是振幅变化因子,其形式如下:
(6)
分别运用5种方法对加噪信号进行分解,每个本征模态分量的曲率曲线如如图4和图5所示,通过

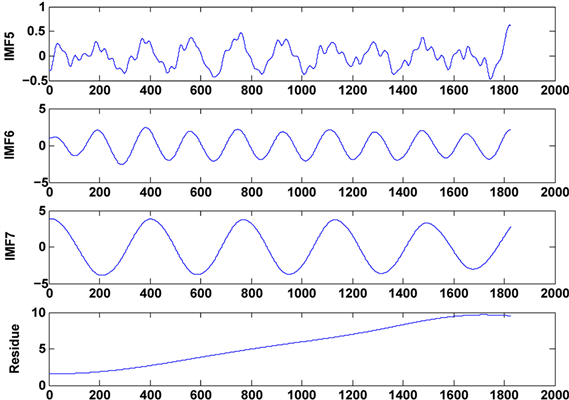
Figure 4. Intrinsic mode component waveform
图4. 本征模态分量波形
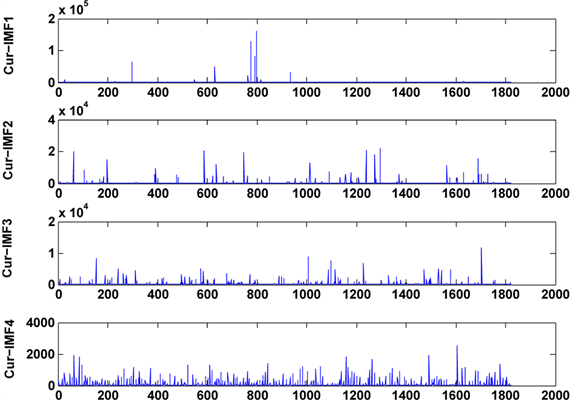
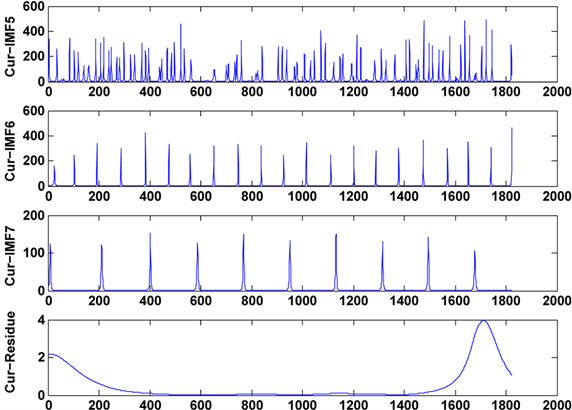
Figure 5. Curvature curve waveform
图5. 本征模态分量的曲率曲线波形
计算每个本征模态分量的曲率曲线与原始信号曲率曲线的离散Frechet距离可以获得k值(如图6所示)。原信号和去噪后的重构信号如图7所示。
采用这5种方法对含噪的模拟信号 进行重构,并比较5种方法的重构效果。为了保证能够准确地评判出本文所提方法的去噪效果,选择信噪比(Signal-Noise Ratio, SNR)、均方根误差(Root Mean Square Error, RMSE)和相关系数(Correlative Codfficient, CC)作为衡量去噪效果的评价指标,评价标准是SNR越高越好,RMSE越小越好,CC越大越好。
图8和表1的实验结果表明,CEEMDAN和ICEEMDAN方法的信噪比较高,均方根误差较小,则
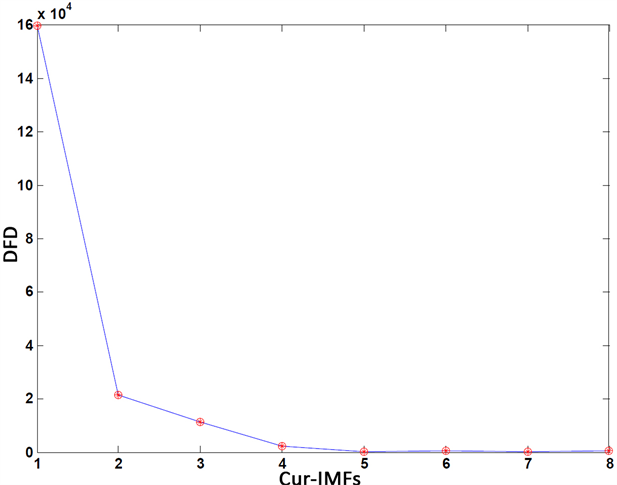
Figure 6. Discrete Frechet distance
图6. 离散Frechet距离
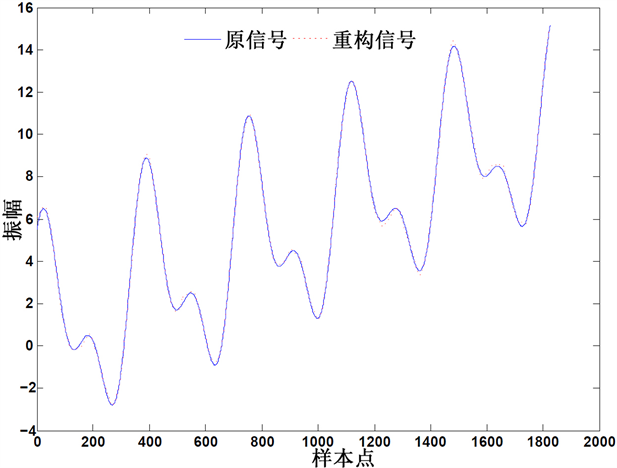
Figure 7. Original signal and reconstructed signal waveform
图7. 原信号和重构信号波形
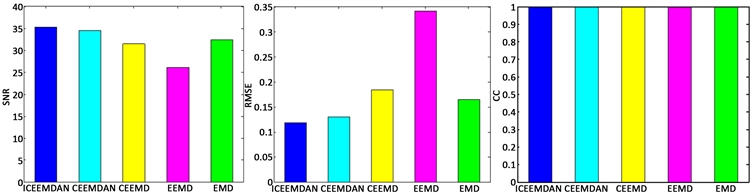
Figure 8. Signal reconstruction effect of 5 kinds of methods
图8. 5种方法的信号重构效果
Table 1. Signal reconstruction effect of 5 kinds of methods
表1. 5种方法的信号重构效果
这两种方法的重构误差较小,精度相对更高。但是,这五种方法的相关系数比较接近,不能判定重构效果。表1分别给出了这5种方法的信噪比、均方根误差和相关系数。综合信噪比、均方根误差和相关系数的结果可知,ICEEMDAN方法在信号去噪及重构中具有较强的鲁棒性,该方法去噪能力强,重构误差小。
5. 结论
本文首先采用EMD、EEMD、CEEMD、CEEMDAN及其ICEEMDAN 5种方法对仿真信号进行分解,其次求出原始信号及分解后的本征模态分量的曲率曲线,并根据原始信号的曲率和分解后的本征模态分量曲率间的离散Frechet距离选择包含有用信号的相关模态分量,最后用这些相关模态分量进行信号重构。根据模拟数据的实验结果,可以得出,经ICEEMDAN方法处理后的数据结果优于其它4种方法,因此,该方法的去噪效果更好。
文章引用
牛淑文. 基于经验模态分解理论的去噪方法研究
The Research of Denoising Method Based on Empirical Mode Decomposition Theory[J]. 应用数学进展, 2017, 06(07): 881-891. http://dx.doi.org/10.12677/AAM.2017.67106
参考文献 (References)
- 1. 李士心, 刘鲁源. 基于小波阈值去噪方法的研究[C]//中国仪器仪表学会. 中国仪器仪表学会第四届青年学术会议: 2002.
- 2. Wang, L., Song, W., and Liu, P. (2016) Link the Remote Sensing Big Data to the image Features via Wavelet Transformation. Cluster Computing, 19, 793-810. https://doi.org/10.1007/s10586-016-0569-6
- 3. Huang, N.E., Shen, Z., Long, S.R., Wu, M.C., Shih, H.H., Zheng, Q., Yen, N., Tung, C.C. and Liu, H.H. (1998) The Empirical Mode Decomposition and the Hilbert Spectrum for Non-Linear and Non-Stationary Time Series Analysis. Proceedings of the Royal Society of London A, 454, 903-995. https://doi.org/10.1098/rspa.1998.0193
- 4. Wu, Z. and Huang, N.E. (2009) Ensemble Empirical Mode Decomposition:A Noise-Assisted Data Analysis Method. Advances in Adaptive Data Analysis, 1, 1-41. https://doi.org/10.1142/S1793536909000047
- 5. Yeh, J.-R., Shieh, J.-S. and Huang, N.E. (2010) Complementary Ensemble Empirical Mode Decomposition: A Novel Noise Enhanced Data Analysis Method. Advances in Adaptive Data Analysis, 2, 135-156. https://doi.org/10.1142/S1793536910000422
- 6. Torres, M.E., Colominas, M.A., Schlotthauer, G. and Flandrin, P. (2011) A Complete Ensemble Empirical Mode Decomposition with Adaptive Noise. In: 2011 IEEE International Conference on Acoustics, Speech and Signal Processing, Prague, 22-27 May 2011, 4144-4147. https://doi.org/10.1109/ICASSP.2011.5947265
- 7. Colominas, M.A., Schlotthauer, G. and Torres, M.E. (2014) Improved Complete Ensemble EMD: A Suitable Tool for Biomedical Signal Processing. Biomedical Signal Processing and Control, 14, 19-29. https://doi.org/10.1016/j.bspc.2014.06.009
- 8. Coolidge, J.L. (1952) The Unsatisfactory Story of Curvature. The American Mathematical Monthly, 59, 375-379. https://doi.org/10.2307/2306807
- 9. Sriraghavendra, R., Karthik, K. and Bhattacharyya, C. (2007) Frechet Distance Based Approach for Searching Online Handwritten Documents. Proceeding ICDAR '07 Proceedings of the Ninth International Conference on Document Analysis and Recognition, Washington DC, 23-26 September 2007, 461-465.
