Advances in Applied Mathematics
Vol.
13
No.
01
(
2024
), Article ID:
79107
,
8
pages
10.12677/AAM.2024.131010
不同代谢目标下甘油代谢通量分布的模型与 计算
王梦婷*,张政颖
福建师范大学数学与统计学院,福建 福州
收稿日期:2023年12月10日;录用日期:2024年1月5日;发布日期:2024年1月12日

摘要
胞内代谢通量的估计可为理解细胞代谢提供帮助。本研究针对肺炎克雷伯式杆菌甘油代谢,以最大化生物量和最大化ATP作为性能指标函数,以代谢通量作为决策变量,并将代谢通量平衡作为约束条件,建立数学规划模型,用以估计连续培养下不同代谢目标的代谢通量分布。数值结果表明对于给定的稀释速率和初始甘油浓度,在最大化生物量下,细胞代谢主要用于细胞生长以及生产1,3-丙二醇,且流向乙酸乙醇和流向生物质的代谢通量有显著差异;在最大化ATP下,代谢主要用于能量的生成,同时流向2,3-丁二醇和甲酸盐以及流向二氧化碳和氢气的代谢通量相差较大。
关键词
通量分布,代谢网络,甘油代谢,线性规划

Model and Calculation of Glycerol Metabolic Flux Distribution under Different Metabolic Targets
Mengting Wang*, Zhengying Zhang
School of Mathematics and Statistics, Fujian Normal University, Fuzhou Fujian
Received: Dec. 10th, 2023; accepted: Jan. 5th, 2024; published: Jan. 12th, 2024

ABSTRACT
The estimation of intracellular metabolic flux is helpful for understanding cellular metabolism. In this paper, a mathematical programming model with the metabolic fluxes as decision variables is proposed for optimizing the flux distribution of glycerol metabolic pathways in Klebsiella pneumoniae, in which mass-balance equations are used as a constraint. In the model, we respectively use the maximization of biomass and ATP as the performance index. Numerical results show that for a given dilution and initial glycerol concentration, the substrate is mainly consumed for cell growth and the production of 1,3-proapanediol if biomass is maximized, and the metabolic flux to HAc and EtOH are significantly lower than that to the biomass. When the production of ATP is maximized, the substrate is mainly used for energy generation, while the metabolic fluxes to 2,3-butanediol and for mate, as well as to CO2 and H2 also differ greatly.
Keywords:Flux Distribution, Metabolic Network, Glycerol Metabolism, Linear Programing

Copyright © 2024 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
1,3-丙二醇是一种重要的有机化学原料,最重要的用途就是作为合成新型聚酯材料聚对苯二甲酸丙二酯醇(PTT)的单体,在聚合物和其他有机化学品的合成中有很多应用,其应用前景广泛 [1] [2] 。化学法和生物法是1,3-丙二醇的两种主要生产方法,近几年,微生物发酵法已经成为当今社会主要关注的焦点,因为相比于化学法,该方法具有条件温和、操作简单、环境污染小、副产物少等诸多优点,具有非常广阔的应用前景 [3] 。甘油是一种可再生的低成本碳源,可通过自然界中的菌种将其转化为1,3-丙二醇,如肺炎克雷伯式杆菌、丁酸梭菌、柠檬酸杆菌、巴氏梭菌等,其中肺炎克雷伯式杆菌因其高生产力而被广泛研究 [4] 。Kumar和Park综述了肺炎克雷伯式杆菌甘油代谢研究的最新进展,以及利用该菌株作为微生物细胞工厂生产1,3-丙二醇的潜力和挑战 [5] 。肺炎克雷伯式杆菌歧化甘油生产1,3-丙二醇已经成为众多学者们所关注的焦点,对于代谢过程,已经有学者应用数学方法对其进行了阐述和说明。
代谢网络可以采用不同类型的调节来显示细胞活动各个级别的生理学调整以及响应环境变化,在过去几十年里,人们为研究代谢网络做出了很多努力 [6] 。代谢网络中,各类组分物质的合成或消耗速率称为代谢通量,细胞内代谢通量定量计算和分析是代谢工程的重要研究内容之一。为此,本文选择肺炎克雷伯式杆菌作为研究对象,分析其代谢网络,并用不同的代谢目标函数来描述代谢通量分布,进而反应并量化生化反应和生命活动规律。
在分析细胞中代谢途径这一方面,通量平衡分析(FBA)是一个经典的研究方法,自被提出以来就受到大量关注 [7] ,并被广泛应用于研究生长特性、解释生长表型和给出预测结果等方面的研究。该方法通常假设细胞内代谢物周围的拟稳态质量平衡。在此基础上,建立一个线性规划模型(LP),它由假设的生物代谢目标和质量平衡约束以及通量的上下限组成。通过求解这个线性规划问题,可以获得路径的通量分布 [8] [9] 。由于求解线性规划在计算上成本低,因此常被用来计算代谢网络的胞内代谢通量。
在实际微生物发酵法生产1,3-丙二醇的过程中,想要准确地预测细胞内的通量分布情况,关键是要建立一个准确的合理的目标函数模型。目前,已有文献对此进行了讨论和研究 [10] 。因此,本研究根据文献的理论,主要考察了最大化生物量和最大化ATP这两个代谢目标在肺炎克雷伯式杆菌歧化甘油生产1,3-丙二醇的代谢通量分布情况,分别以通量平衡方程为约束条件,以代谢通量为决策变量,对不同代谢目标下的代谢通量进行求解,模拟了在同一稀释速率和初始甘油浓度下的通量分布,并对其进行讨论。
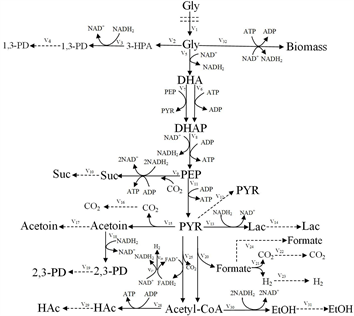
Figure 1. Main pathways of anaerobic glycerol metabolism in Klebsiella pneumoniae
图1. 肺炎克雷伯式杆菌厌氧甘油代谢的主要路径
2. 代谢反应网络
根据文献 [4] [11] ,肺炎克雷伯式杆菌以甘油为底物生产1,3-PD,其主要代谢网络如图1所示。
甘油被运输到细胞内之后,经过一系列代谢反应后,主要生成1,3-丙二醇和其他副产物。总体代谢过程分为还原和氧化两个分支途径。在还原途径中,第一步,在甘油脱水酶(GDHt)的作用下,甘油脱水转化为中间体3-羟基丙醛(3-HPA);第二步,3-HPA在1,3-丙二醇氧化还原酶(PDOR)的催化最终生成产物1,3-丙二醇。在氧化途径中,甘油脱氢酶(GDH)催化甘油转化为二羟基丙酮(DHA),而后经二羟基丙酮激酶(DHAK)催化生成磷酸二羟基丙酮(DHAP),此后通过糖酵解进入丙酮酸(PYR)中心代谢,丙酮酸对不同的发酵产物发生反应,如乙酸(EtOH)、乙醇(HAc)、2,3-丁二醇(2,3-BD)和乳酸(Lac)等。氧化还原反应构成了甘油在肺炎克雷伯式杆菌中的代谢过程,因为氧化途径为生物质的合成提供能量和碳成分,还原途径依赖于还原当量(NADH)和能量物质三磷酸腺苷(ATP),使甘油得以氧化同化。
图1中的代谢网络由32个胞内反应和20个代谢物组成,我们假设细胞的代谢处于拟稳态,那么所有中间代谢物的平衡方程由表1给出,其中 为第i个细胞内代谢物(mmol∙g−1), 为第j个代谢通量(mmol∙g−1∙h−1), 表示第i种代谢物的变化速率(mmol∙g−1∙h−1)。
3. 数学模型
本节旨在建立肺炎克雷伯式杆菌甘油代谢过程的数学模型,来描述在不同代谢目标下胞内代谢通量的分布情况。
3.1. 代谢通量模型
通量平衡分析是分析代谢网络中代谢物通量的数学方法,通过计算胞内代谢物的通量,可以预测某个特定代谢物的生产速率。微生物发酵的化学计量在数学上可以表示为线性微分方程,则代谢物浓度随时间变化的方程可以表示为:
Table 1. Stoichiometric equations of metabolic fluxes
表1. 代谢通量的化学计量方程
(1)
其中, 是细胞内代谢物浓度(mmol∙g−1), 是一个20 × 32维的化学计量矩阵(代谢物组成此矩阵的行,反应组成此矩阵的列),化学计量系数 表示第j个反应中第i个代谢物, 是代谢通量的向量(mmol∙g−1∙h−1), 是代谢物浓度变化率的向量值函数。特别地,当 时,意味着该代谢物达到了拟稳态。此方法的优点是可用简单的线性方程组描述繁琐的反应过程,而对于线性系统而言,就有比较丰富的有效分析与计算方法。
在拟稳态前提下,假设细胞内的中间代谢物均处于拟稳态,即其浓度变化速率为0,这样由n个中间代谢物即可得到n个关于速率的约束条件,若关注的速率总数目为J,那么待解问题的自由度为 。这样通过实验测出K个独立的代谢速率可确定所有的通量分布。因此细胞内代谢物的拟稳态用以下线性方程来描述:
(2)
这些方程通常被称为质量平衡方程。具体到本文, 为表1中 的右端项系数构成的化学计量矩阵。由于能量消耗量一定不超过能量生成量,才能维持生物合成过程,因此本研究中对于ATP的生产可以积累,不必要求该项平衡方程为0。
3.2. 甘油代谢目标模型
在通量平衡约束条件下,针对肺炎克雷伯式杆菌歧化甘油生产1,3-丙二醇的代谢过程,本节主要考察了以最大化生物量和最大化ATP作为代谢目标在代谢过程中代谢通量的分布情况,分别以这两个代谢目标作为性能指标函数,将代谢通量作为决策变量,建立线性规划模型。
模型1:将最大化生物量作为代谢目标函数,以质量平衡方程作为约束条件,建立如下模型:
(3)
其中,d是固定值,即甘油输入量。
模型2:将最大化ATP作为代谢目标函数,以质量平衡方程作为约束条件,建立如下模型:
对于模型1和模型2的求解,由于两个模型都是线性规划问题,因此可利用MATLAB的linprog函数包求解该线性规划问题。对于所得结果利用柱状图对不同代谢目标下的代谢通量进行比较,如图2和图3所示。
4. 结果和讨论
基于模型1和模型2,本研究模拟了在同一稀释速率和初始甘油浓度下的代谢通量分布,稀释速率为0.15 h−1,初始甘油浓度为809 mmol∙g−1,那么代谢通量v1为25.28 mmol∙g−1。通过对模型1和模型2进行求解,得到不同代谢目标下的通量分布,如图2和图3所示,其中蓝色表示模型1的求解结果,橙色表示模型2的求解结果。数值结果显示,在不同的代谢目标下,代谢通量分布的侧重点有所不同。图中显示,代谢目标为最大化生物量时,甘油代谢的分布是由单一的细胞驱动力支配,生物质生产是驱动肺炎克雷伯式杆菌甘油代谢的主要力量,代谢通量主要流向维持细胞生长以及生成产物1,3-丙二醇,且流向乙酸乙醇的和流向生物质的代谢通量相差较大。在最大化ATP下,代谢通量主要用于能量的产生,同时流向2,3-丁二醇和甲酸盐的代谢通量差别较大,以及流向 的代谢通量有显著差异。
在本文的研究中,我们没有模拟细胞内代谢物的浓度,与动态通量平衡分析上的许多其他工作类似,我们做了一个共同的假设,即细胞内动力学保持拟稳态状态,这意味着在所提出的模型中忽略了初始发酵阶段,并且假设细胞内代谢物的浓度保持不变。拟稳态假设通常适用于细胞内动力学的分析,因为许多扰动实验表明,拟稳态状态通常在环境扰动后的几秒钟或者几分钟内达到,这比整个培养过程的时间尺度要短得多 [10] [12] 。然而,忽略细胞内浓度内可能会导致数值计算中的一些技术问题。例如,在模拟底物限制过程中,一些物质的浓度可能会降到零,在这种情况下,细胞内环境的输入通量将在这些时间瞬间消失,导致由大多数零通量分布。

Figure 2. The metabolic fluxes distributions of Model 1 and Model 2 ( )
图2. 模型1和模型2的通量分布( )

Figure 3. The metabolic fluxes distributions of Model 1 and Model 2 ( )
图3. 模型1和模型2的通量分布( )
5. 结论
细胞代谢的数学模型对于预测胞内代谢通量分布起着重要的作用。本文针对肺炎克雷伯式杆菌歧化甘油生产1,3-丙二醇的生物发酵过程,以质量平衡方程为约束条件,将代谢通量视为决策变量,建立了以最大化生物量和最大化ATP为代谢目标的线性规划模型,我们估计了在不同代谢目标下细胞内的代谢通量分布情况。计算结果表明在给定稀释速率和初始甘油浓度下,当代谢目标为最大化生物量时,流向乙酸乙醇和流向生物质的代谢通量相差较大。代谢目标为最大化ATP时,流向2,3-丁二醇和甲酸盐的代谢通量有显著差异,以及流向 的代谢通量差别较大。本文的研究可为进一步理解肺炎克雷伯式杆菌歧化甘油生产1,3-丙二醇这一代谢过程提供理论参考。
基金项目
福建省自然科学基金(No. 2021J01660)。
文章引用
王梦婷,张政颖. 不同代谢目标下甘油代谢通量分布的模型与计算
Model and Calculation of Glycerol Metabolic Flux Distribution under Different Metabolic Targets[J]. 应用数学进展, 2024, 13(01): 76-83. https://doi.org/10.12677/AAM.2024.131010
参考文献
- 1. Zhang, Q. and Xiu, Z. (2009) Metabolic Pathway Analysis of Glycerol Metabolic in Klebsiella pneumonia Incorporat-ing Oxygen Regulatory System. Biotechnology Progress, 25, 103-115. https://doi.org/10.1002/btpr.70
- 2. Pan, D., Wang, X., Shi, H., Yuan, D. and Xiu, Z. (2018) Dynamic Flux Balance Analysis for Microbial Conversion of Glyc-erol into 1,3-Propanediol by Klebsiella pneumoniae. Bioprocess and Biosystems Engineering, 41, 1793-1805. https://doi.org/10.1007/s00449-018-2002-4
- 3. Lama, S., Ro, S., Seol, E., Sekar, B., Ainala, S., Thangappan, J., Song, H., Seung, D. and Park, S. (2015) Characterization of 1,3-Propanediol Oxidoreductase (DhaT) for Klebsiella pneumoniae J2B. Biotechnology and Bioprocess Engineering, 20, 971-979. https://doi.org/10.1007/s12257-015-0635-6
- 4. Chen, X., Xiu, Z., Wang, J., Zhang, D. and Xu, P. (2003) Stoi-chiometric Analysis and Experimental Investigation of Glycerol Bioconversion to 1,3-Propanediol by Klebsiella pneu-moniae under Microaerobic Conditions. Enzyme Microbial Technology, 33, 386-394. https://doi.org/10.1016/S0141-0229(03)00135-2
- 5. Kumar, V. and Park, S. (2018) Potential and Limitations of Klebsiella pneumoniae as a Microbial Cell Factory Utilizing Glycerol as the Carbon Source. Biotechnology Advances, 36, 150-167. https://doi.org/10.1016/j.biotechadv.2017.10.004
- 6. Jeong, H, Tombor, B, Abert, R., Oltvai, Z. and Barabási. A. (2000) The Large-Scale Organization of Metabolic Networks. Nature, 40, 651-654. https://doi.org/10.1038/35036627
- 7. Orth, J., Thiele, I. and Palsson, B. (2010) What Is Flux Balance Analysis? Nature Biotechnology, 28, 245-248. https://doi.org/10.1038/nbt.1614
- 8. Varma, A. and Palsson, B. (1994) Stoichiometric Flux Balance Models Quantitatively Predict Growth and Metabolic by-Product Secretion in Wild-Type Escherichia coli W3110. Applied and Environmental Microbiology, 60, 3724-3731. https://doi.org/10.1128/aem.60.10.3724-3731.1994
- 9. Edwards, J., Covert, M. and Palsson, B. (2002) Metabolic Modelling of Microbes: The Flux-Balance Approach. Environmental Mi-crobiology, 4, 133-140. https://doi.org/10.1046/j.1462-2920.2002.00282.x
- 10. Suchuetz, R., Kuepfer, L. and Sauer, U. (2007) Systematic Evaluation of Objective Functions for Predicting Intracellular Fluxes in Escherichia coli. Molecular Systems Biology, 3, 922-929. https://doi.org/10.1038/msb4100162
- 11. Sun, Y., Ye, J., Mu, X., Teng, H., Feng, E., Zeng, A. and Xiu, Z. (2012) Nonlinear Mathematical Simulation and Analysis of Dha Regulon for Glyc-erol Metabolism in Klebsiella pneumoniae. Chinese Journal of Chemical Engineering, 20, 958-970. https://doi.org/10.1016/S1004-9541(12)60424-8
- 12. Zhang, Q., Teng, H., Sun, Y. and Xiu, Z. (2007) Metabolic Flux Analysis of Bioconversion of Glycerol into 1,3-Propanediol by Klebsiella pneumoniae. 2007 1st International Con-ference on Bioinformatics and Biomedical Engineering, Wuhan, 6-8 July 2007, 1269-1272. https://doi.org/10.1109/ICBBE.2007.327
附录
为了阅读方便,将本文化学物简写进行说明,如附表1所示:
Table S1. Abbreviations of metabolites and enzymes/proteins involved in anaerobic glycerol metabolism by Klebsiella pneumoniae
附表1. 肺炎克雷伯氏菌参与厌氧甘油代谢的代谢物和酶/蛋白的缩写
NOTES
*通讯作者。
