ABSTRACT

The course of Mechanics of Materials involves some abstract concepts and obscure theories. It is noted in the teaching that most of students are generally aware of the difficulties of those concepts and theories. This paper proposes to introduce the ABAQUS finite element numerical analysis in the teaching of Mechanics of Materials. Taking the advantages of the dynamic visualization function, the interest of the students can be compelled, the understanding of the abstract concepts and theories can be deepened and the current situation of numerical methods less applied in traditional teaching can be improved. Therefore, the application of ABAQUS in the teaching of Mechanics of Materials is able to help improve the teaching effect and efficiency.

Keywords:Mechanics of Materials, Course Teaching, ABAQUS Finite Element Software

在材料力学教学中引入ABAQUS有限元 数值分析的探讨

李明耀^*，左建平，李英杰，薛东杰，刘德军

中国矿业大学(北京)力学与建筑工程学院，北京

收稿日期：2019年3月26日；录用日期：2019年4月10日；发布日期：2019年4月17日

摘 要

材料力学课程涉及一些抽象的概念和晦涩难懂的理论，在教学过程中发现学生普遍掌握困难。本文提出将ABAQUS有限元数值分析应用在材料力学教学中，利用其动态可视化功能增加学生的兴趣，加深学生对抽象概念和理论的理解，克服传统教学中较少应用数值方法的现状，从而达到改善材料力学课程教学效果的目的。

关键词 :材料力学，课程教学，ABAQUS有限元软件

Copyright © 2019 by authors and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

材料力学是力学、机械工程、土木工程等专业的核心必修课，旨在使学生掌握物体机械运动的一般规律及其研究方法，培养和提高学生的逻辑思维能力、抽象简化和数学计算等方面的能力。由于课程本身涉及大量的理论概念，公式推导和数学计算，学生对抽象概念的理解不够深刻，公式推导晦涩难懂，试验原理和过程的感性认知不够，简化模型的数学计算与对应的工程实际间的联系缺乏足够的探讨和研究等，导致课程的教学效果不佳。ABAQUS有限元软件可以处理工程中许多从简单到复杂的线性和非线性问题，能对材料力学中许多问题进行分析计算和数值模拟，提供强大的动态可视化功能，实现全场模拟，使学生直观感性地认识和理解复杂的工程问题和抽象概念。对于应用数值分析较少的材料力学课程教学来说，引入ABAQUS有限元数值分析具有积极的促进作用 [1] 。

因此，本文提出将ABAQUS有限元数值分析应用在材料力学教学中，通过有限元建模过程，加深学生对力学模型的理解，包括模型简化、边界条件和载荷的施加以及分析过程的选择等。在教学中引入数值分析，使学生更直观地了解实际工程问题的简化和分析过程，从而激发学生的兴趣，增强学生对工程问题的认识和解决工程问题的能力，对材料力学的教学方法具有重要的促进作用和补充意义。

2. 在材料力学教学中引入ABAQUS有限元数值分析的探讨

目前，大多数材料力学教学采用传统的教学模式，在课堂上会用大部分时间讲解基本概念、基本原理和公式推导。在这样的条件下，学生很难深入理解一些抽象的概念，对公式推导和实验原理的感性认识不够。学生普遍缺乏将材料力学中涉及的强度、刚度和稳定性等数学计算与工程实际建立联系的深入探讨和研究，只能被动接受知识的灌输而难以激发学习的主动性，导致教学效果不佳。

针对以上问题，本文提出将ABAQUS有限元数值分析应用在材料力学教学中值得探讨。首先，ABAQUS不仅能提供力学计算和分析，更有强大的可视化功能。ABAQU的建模过程涉及载荷和边界条件的施加，可以帮助学生直观理解静力学中受力分析过程和结构计算简图。其强大的后处理能提供动态可视化过程，使学生能感性认识并深刻理解原本抽象的力学概念。其次，传统力学实验教学一般课时少且受实验耗材限制，无法重复实验去深入研究和分析试验中涉及的力学问题，限制了实验教学的效果。ABAQUS有限元数值分析不仅能模拟力学实验过程，且能不断重复和动态可视化分析试验结果。还允许学生修改模型参数或材料本构模型来测试不同材料在不同阶段的变形特性，帮助学生不断探索和分析力学试验中涉及的力学问题，培养和提高学生分析问题和解决问题的能力，激发学生的学习兴趣和创新思维。此外，材料力学课程涉及的拉、剪、扭、弯问题的分析、设计和校核，在教学过程中发现，学生普遍认为计算过程枯燥乏味，只能被动套公式而难以激发学生的主观能动性。ABAQUS能针对性的提供数值分析，不仅可以加深学生对理论公式的理解，还可以帮助学生发动主观能动性去探索新的相关问题的研究，例如载荷、截面面积、支座反力等对结果的影响规律。

通过上述分析可见，引入ABAQUS能帮助学生直观认识和深刻理解抽象的概念，补充实验教学的不足，既能提高学生的学习兴趣和主观能动性，又能增强学生对工程实际问题的感性认识和解决工程实际问题的能力，为以后的工作和科研奠定基础。

3. 教学案例——带孔平板的应力集中问题

3.1. 问题描述

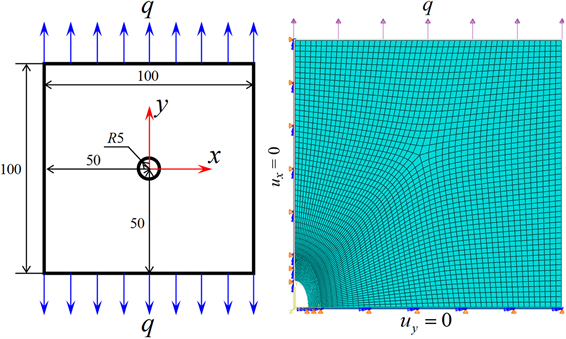
圆孔的孔边应力集中问题存在于许多工程结构中，对孔边应力集中问题的理解和认识具有十分重要的工程意义 [2] [3] 。本节以材料力学中经典的中心带有小孔的有限宽平板的应力集中问题为例，利用ABAQUS对其进行有限元分析，阐述将ABAQUS引入到材料力学教学中的方法和教学效果。如图1(a)所示，一个半径为5 mm的圆孔位于边长为 $100\times 100\text{mm}$ 的平板中心，平板上下两端受均布拉力载荷 $q=100\text{MPa}$ ，平板材料为线弹性，其弹性模量 $E=210\text{GPa}$ ，泊松比 $v=0.3$ 。

图1. 带孔平板应力集中问题模型；(a) 力学模型；(b) ABAQUS有限元模型

3.2. ABAQUS有限元数值分析

平板厚度远远小于板宽，可将其视为平面应力问题。通过分析结构和载荷的对称性，只需取其中的1/4进行分析，如图1(b)所示，载荷和边界条件为：

$x=0,u_x=0;y=0,u_y=0;x=\frac{L}{2},q=100\text{MPa};y=-\frac{L}{2},q=100\text{MPa}$ (1)

由于圆孔附近会出现应力集中，为了保证计算精度，对圆孔附近区域的网格进行细化，其他区域采用较粗网格来保证计算效率。为了保证应力集中的计算精度，模型均采用二次完全积分单元(CPS8) [4] [5] 。

通过上述ABAQUS建模过程可见，学生必须首先能从简单的工程问题中抽象出理论力学模型，包括几何模型、物理模型、载荷及边界条件等。其次，必须通过对实际工程问题的分析和理解，提出正确的建模方法(例如，根据对称性采用1/4模型替代完整模型)和工程问题的合理简化(例如采用平面应力问题)。这个过程能使学生对实际工程问题更加深刻地理解，对材料力学课程中的基本概念和方法产生更加直观的认识，进一步激发学生的兴趣从而提高教学效果。

3.3. 应力集中现象的可视化

ABAQUS在后处理中的可视化(Visualization)模块中提供了应力、位移、应变等信息的云图。如图2(a)所示，受竖向拉载荷作用，加载方向的局部应力分布云图显示了孔边应力集中现象，即圆孔边左右两边集中了少量红色区域，其应力明显高于远离孔处的应力，最高值达到308.65 MPa，而远离孔边大部分区域的应力约为100 MPa。为了验证有限元计算的正确性，对比经典弹性力学理论对带孔的无限大平板中的应力解析解可知，在x轴方向上的环向正应力为：

${\sigma }_{\phi }=q\left(1+\frac{1}{2}\frac{R^2}{{\rho }^2}+\frac{3}{2}\frac{R^4}{{\rho }^4}\right)$ (2)

由上述解析解可知，在孔边即 $\rho =R$ 时，应力最大值为 ${\sigma }_{\max }=3q$ 。与此同时，在远离圆孔即 $\rho$ 逐渐增大时，应力急剧趋近于 $q$ 。由此可知，ABAQUS有限元计算的应力分布与弹性理论计算的解析解完全一致。

图2. 应力集中现象的ABAQUS可视化；(a) 孔口边应力集中局部图；(b) 应力云图和截面上的应力分布曲线

ABAQUS可视化功能清楚地显示整体结构的应力分布，在过圆孔中心x方向的1-1截面和几倍孔径外的2-2截面上分别画出相应的应力曲线，如图2(b)所示。在1-1截面上，孔边的应力远大于几倍孔径以外的应力，而应力随着据孔的距离增大而越快地趋近于无孔时的应力。在远离圆孔的2-2截面上，圆孔对应力分布的影响仅局限于孔的附近区域，在距离孔较远的地方应力几乎不受孔的影响，这就是圣维南原理。

由此可见，ABAQUS的可视化模块能更直观地提供应力的分布情况，能让学生对应力集中这样的抽象概念有更加直观的视觉冲击和感性认识，同时能激发学生的学习兴趣，进一步提高教学效果。

3.4. 孔的形状对应力集中的影响分析

应力集中的程度，与孔的几何形状有关。孔的形状越尖锐，应力越集中。如何让学生深刻理解这样的抽象概念一直以来是教学中的难题。受实验耗材的限制，无法重复做实验去深入研究不同几何形状的小孔，限制了实验教学的效果。理论分析仅能解决部分规则几何形状的问题，对于复杂的问题仍是束手无策。相反地，ABAQUS不仅能模拟力学实验过程，且能不断重复和动态可视化分析试验结果，能补充力学实验和理论教学中的不足。下面以孔的形状对应力集中的影响分析为例，进一步探讨ABAQUS在教学中的优势。

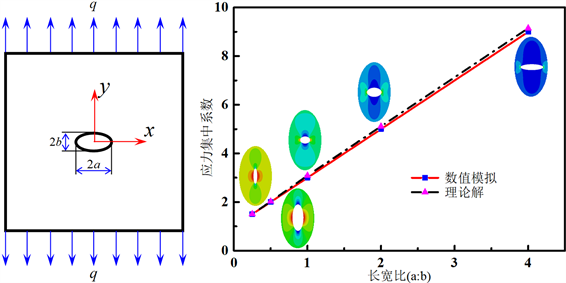
以椭圆形小孔为例，通过改变长短轴比值来对比分析不同小孔形状对应力集中的影响规律，进一步加深学生对应力集中概念的理解。力学模型如图3(a)所示，椭圆孔长轴和短轴分别为2a和2b，材料属性、边界条件和载荷与前述问题一致。考察五种椭圆的长短轴之比的情况，通过ABAQUS分析计算，薄板中椭圆孔口附近的应力分布如图3所示。可以看出，随着长短轴之比逐渐增大，应力集中现象趋于显著，从应力云图中可以直接观察到在长短轴之比较小时，红色区域占比较多；较大时，红色区域集中于椭圆尖端附近的而使应力显著增加。通过对比应力集中系数( $k={\sigma }_{\max }/q$ )的理论和数值分析结果，二者几何一致。由此可见，ABAQUS不仅能够提供与理论解一致的数值解，还能通过可视化模块显示应力集中的程度和分布情况，能让学生更直观地观察到应力集中受孔的几何形状的影响规律，能有效补充材料力学中的试验和理论教学的不足。

图3. 应力集中现象的ABAQUS可视化；(a) 力学模型；(b) 数值分析解与理论界对比

3.5. 塑性屈服对应力集中的影响分析

不同材料对应力集中的敏感程度不同，对于脆性材料，应力集中的影响是致命的，不加以限制和约束，将引起极大的工程问题；相反地，对于塑性材料，可以不考虑应力集中的影响。材料力学教学中的解释对于本科生来说是晦涩难懂的，这也是材料力学教学中经常遇到的一种难处。

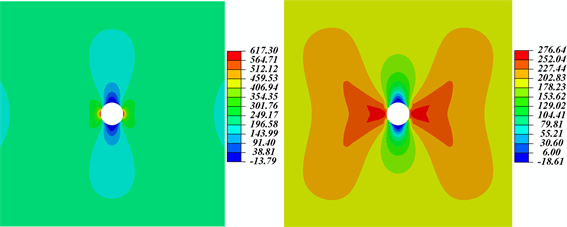
为了帮助学生更深入的理解，采用ABAQUS对弹性材料与相应的塑性材料进行对比分析，可以直观地展示出弹脆性材料中的应力集中突出问题和塑性材料中的屈服对应力集中的限制。如图4(a)所示，由于弹性材料没有塑性屈服，随着载荷的增加，应力集中现象愈加突出。相反，相应的塑性材料，同样的加载条件下，不再出现显著的应力集中现象(如图4(a)红色区域)，取而代之的是大面积的塑性屈服区(如图4(b)的红色区域)。图4(a)无屈服极限的情况下，应力集中处的最大应力可以达到617.30 MPa，而图4(b)有屈服极限的情况下，最大应力仅为276.64 MPa。由此可见，塑性材料对于应力集中不敏感，塑性现象有缓和应力集中的作用；而弹性材料在应力集中出会迅速产生大于拉伸强度的应力而易发生局部破坏。

图4. 材料性质对圆孔边应力集中的影响；(a) 弹性材料；(b) 塑性材料

由此可见，ABAQUS可视化功能可以直观地展示应力集中和塑性屈服现象，能帮助学生更好地理解应力集中现象和塑性屈服对应力集中的缓和作用。相比于传统的概念讲述，ABAQUS的应用能激发学生的兴趣，促进教学效果。

4. 结论

本文提出将ABAQUS有限元数值分析引入到材料力学课程中来提高教学效果，以平板中圆孔应力集中现象为例，探讨了应力集中现象的可视化、不同几何形状和塑性屈服对应力集中的影响。通过案例分析发现，结合ABAQUS有限元数值分析和可视化功能，能使学生在课堂上直观深入地理解抽象的概念，有效补充材料力学中的试验和理论教学的不足，增强学生对工程实际问题的感性认识和解决工程实际问题的能力，激发学生的兴趣和主观能动性，从而提高教学效果。

基金项目

本论文的研究得到国家自然科学基金青年科学基金(11802332)和中央高校基本科研业务费青年专项资金(2018QL04)的支持。

文章引用

李明耀,左建平,李英杰,薛东杰,刘德军. 在材料力学教学中引入ABAQUS有限元数值分析的探讨
Discussion on the Introduction of ABAQUS Finite Element Analysis in Teaching Mechanics of Materials[J]. 创新教育研究, 2019, 07(02): 178-183. https://doi.org/10.12677/CES.2019.72032

参考文献