Pure Mathematics
Vol.05 No.05(2015), Article ID:16102,8
pages
10.12677/PM.2015.55035
Two Preserver Problems on Induced Maps
Panpan Yan, Jun Zhang, Chongguang Cao
School of Mathematical Science, Heilongjiang University, Harbin Heilongjiang
Email: 492689647@qq.com
Received: Sep. 8th, 2015; accepted: Sep. 25th, 2015; published: Sep. 28th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Let F be a field, Mn(F) be the set of alln × nmatrices over F. If a map f: Mn(F) → Mn(F) is defined by , where
, where  are the set of functions on F, then f is called a map induced by
are the set of functions on F, then f is called a map induced by  on Mn(F). If AB = BA implies f(A)f(B) = f(B)f(A), then f is called preserving commutativity of matrices. If B2 = B implies (f(B))2 = f(B), then f is called preserving idempotent matrices. In this paper, we characterize induced maps preserving idempotence and commutativity of matrices over fields, resprectively.
on Mn(F). If AB = BA implies f(A)f(B) = f(B)f(A), then f is called preserving commutativity of matrices. If B2 = B implies (f(B))2 = f(B), then f is called preserving idempotent matrices. In this paper, we characterize induced maps preserving idempotence and commutativity of matrices over fields, resprectively.
Keywords:Field, Matrix, Preserving Commutativity, Preserving Idempotence, Induced Map

关于诱导映射的两个保持问题
闫盼盼,张隽,曹重光
黑龙江大学数学科学学院,黑龙江 哈尔滨
Email: 492689647@qq.com
收稿日期:2015年9月8日;录用日期:2015年9月25日;发布日期:2015年9月28日

摘 要
令F是一个域,Mn(F)是F上所有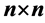 矩阵的集合。如果一个映射
矩阵的集合。如果一个映射 被定义如下,
被定义如下,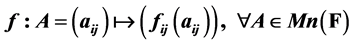 其中
其中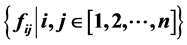 是关于F的函数集,则称f是
是关于F的函数集,则称f是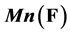 的由
的由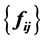 诱导的映射。如果AB = BA意味着
诱导的映射。如果AB = BA意味着 ,则f被称为保交换矩阵。如果
,则f被称为保交换矩阵。如果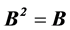 意味着
意味着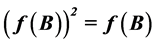 ,则f被称为保幂等矩阵。本文我们分别刻画保域上矩阵幂等性及交换性的诱导映射。
,则f被称为保幂等矩阵。本文我们分别刻画保域上矩阵幂等性及交换性的诱导映射。
关键词 :域,矩阵,保交换,保幂等,诱导映射

1. 引言
近年来刻画矩阵集合保持某些性质的映射的研究更感兴趣于映射没有线性和加法假定的情形,例如[1] -[5] 。本文研究的诱导映射,其实也是这类问题的一种。同类研究看[6] 和[7] 。
设F是一个域,Mn(F)是F上所有n 阶矩阵的集合。设f是Mn(F)到自身的映射。fij是F上的函数,其中 。如果定义
。如果定义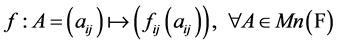 则称f是由{fij}诱导的映射。简称Mn(F)的诱导映射。
则称f是由{fij}诱导的映射。简称Mn(F)的诱导映射。
如果 意味着
意味着 ,则f被称为保交换矩阵。
,则f被称为保交换矩阵。
在本文中用K记Mn(F)中所有幂等阵(B2 = B)的集合,令f是Mn(F)到自身的诱导映射,如果 意味着
意味着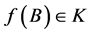 则称f保幂等。本文目的是分别刻画Mn(F)的保幂等及保交换的诱导映射。
则称f保幂等。本文目的是分别刻画Mn(F)的保幂等及保交换的诱导映射。
在本文中用F*记F中所有非0元的集合, 表示(i,j)位置是1,其余位置是零的矩阵。记
表示(i,j)位置是1,其余位置是零的矩阵。记 。
。
2. 保矩阵的幂等性
在f(0) = 0的情况下,对于f为Mn(F)的保幂等的诱导映射的充要条件,我们有如下的重要结果。
定理2.1:设F为一个域,n为整数且n ≥ 3。f是Mn(F)的诱导映射且f(0) = 0,则f保幂等当且仅当f为如下两种形式之一。
(i) 当A为幂等阵时,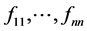 为值域为{0,1}的函数,A为其它矩阵时,
为值域为{0,1}的函数,A为其它矩阵时,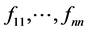 任意,
任意,
 (1)
(1)
(ii) 存在一个可逆对角阵 及F上的一个单自同态
及F上的一个单自同态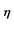 ,使得:
,使得:
 (2)
(2)
其中 。
。
证明:充分性显然,下证必要性。假设 ,且互不相等,由
,且互不相等,由 及f保幂等,看
及f保幂等,看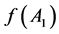 的(i,j)位置得:
的(i,j)位置得:
 (3)
(3)
下面分两种情况讨论。
(i) 存在某 及
及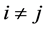 使
使 。
。
此时由(3)易证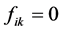 ,再由
,再由 可知
可知 ,进一步由
,进一步由 可得
可得 ,类似可证
,类似可证 ,
, ,
,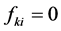 。进一步运用此法可证得对任意
。进一步运用此法可证得对任意 有
有 。
。
这意味着
由 保幂等,不难推出形式(1)。
保幂等,不难推出形式(1)。
(ii) 对于任意不同的 由及任意
由及任意 均有
均有 。
。
由 和
和 保幂等,得
保幂等,得 。利用(3)看
。利用(3)看 位置,可得
位置,可得 ,又由
,又由
已知得 。同理可得
。同理可得 。因此,
。因此,
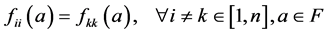 (4)
(4)
类似有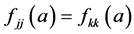 ,因此有
,因此有
 (5)
(5)
对于任意的 ,由
,由 可知
可知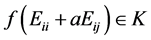 。因此,
。因此,
 (6)
(6)
在(3)中取 可得
可得 于是有
于是有
 (7)
(7)
对于任意不同的 和
和 。由
。由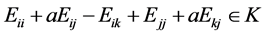 ,看
,看 位置,得到
位置,得到 ,由(3)和(6)得到
,由(3)和(6)得到 。同理可证,
。同理可证,
 (8)
(8)
令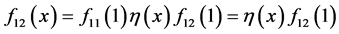 ,
, 。
。
首先,设对于 ,由(3)和(7)得,
,由(3)和(7)得,

其次,令 ,显然有
,显然有 。由(3)可得
。由(3)可得

最后,令 ,由(3)和(7)可得
,由(3)和(7)可得
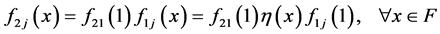
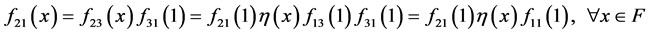
同理可得


因此,得到
 (9)
(9)
对于任意不同的 和
和 ,由
,由 ,得
,得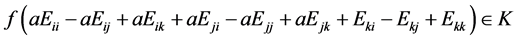 ,由((6)和(8)得,
,由((6)和(8)得, 从(4),定义
从(4),定义 ,
, 。又(9),得到
。又(9),得到
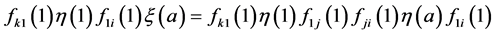 。再由
。再由 和(7)式,得到
和(7)式,得到

将(9)代入(3),又由 和(7),可得
和(7),可得
 (10)
(10)
对于任意不同的 和
和 ,由
,由

得到

又由(9)和(10),得到
 (11)
(11)
应用(10),将(11)两边乘 ,得到
,得到
 (12)
(12)
当 时,运用(8),易证(13)仍成立。从
时,运用(8),易证(13)仍成立。从 ,(9),(10)和(12),知
,(9),(10)和(12),知 是
是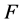 上的一个单自同态。应用(7)和(9),有
上的一个单自同态。应用(7)和(9),有
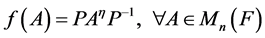
其中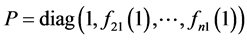 为一个可逆对角阵,证毕。
为一个可逆对角阵,证毕。
定理2.2: 是一个域,若
是一个域,若 为一个由函数
为一个由函数 导出的映射,满足
导出的映射,满足 ,则
,则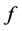 保幂等当且仅当下列(i) (ii)之一成立。
保幂等当且仅当下列(i) (ii)之一成立。
(i) 当 时,
时, ,
, 及
及 是值为0,1的函数,其它情况下
是值为0,1的函数,其它情况下 及
及 任意,
任意, 仍为对角阵。
仍为对角阵。
(ii) 由 可推出
可推出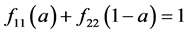 及
及 。
。
证明:
充分性:注意到二阶幂等阵集

结论不难被证。
必要性:由 保幂等,得
保幂等,得 得
得 或0,可推出(i)。同理,当
或0,可推出(i)。同理,当 时有
时有 ,若
,若 ,可推出
,可推出 ,推出(i)。若
,推出(i)。若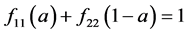 ,可推出
,可推出 ,推出(ii),证毕。
,推出(ii),证毕。
下面我们将用一个例子说明满足定理1.2中(ii)的条件的 也未必是标准的。
也未必是标准的。
例2.3:令 为一个至少包含3个元素的域,设
为一个至少包含3个元素的域,设 为一个由函数
为一个由函数 诱导的。
诱导的。
 。显然,
。显然, 且
且 满足定理2.2中(ii)的条件,因此运用定理2.2可知
满足定理2.2中(ii)的条件,因此运用定理2.2可知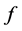 保幂等。但是这个形式与定理2.1中的(ii)形式不同,事实上,当
保幂等。但是这个形式与定理2.1中的(ii)形式不同,事实上,当 且
且 有
有 ,然而
,然而 不是标准的,单射
不是标准的,单射 不存在。
不存在。
注记2.4:如果在定理2.1及2.2中去掉条件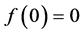 ,结论将更加复杂,例如
,结论将更加复杂,例如 ,
,
其中 为任意固定的矩阵,易见
为任意固定的矩阵,易见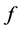 保幂等。
保幂等。
3. 保矩阵的交换性
定理3.1:本节我们研究保矩阵交换性的诱导映射,在一定条件下给出映射的形式。
 是一个域,
是一个域, 为
为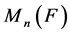 的诱导映射,
的诱导映射, 且满足
且满足 ,
, :
:
(i)当 时,则
时,则 是保交换性的。
是保交换性的。
(ii)当 时,则
时,则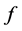 保交换
保交换
 有下列两种形式之一。
有下列两种形式之一。
(1)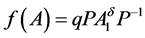 ,
,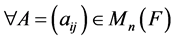 ,其中
,其中 为
为 阶可逆对角阵,
阶可逆对角阵, 为
为 的单自同态,
的单自同态, ,
,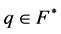 。
。
(2) 。
。
(iii)当 时,
时, 保交换当且仅当下列(1)(2)之一成立。
保交换当且仅当下列(1)(2)之一成立。
(1) 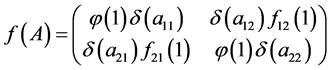
其中 为
为 的自同态,
的自同态, 至少其一不为0。
至少其一不为0。
(2) 
证明(i)显然成立。
(ii)充分性显然,下证必要性。
设 ,且互不相等,
,且互不相等,
令 ,
,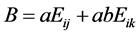 易见
易见 ,由
,由 保交换知
保交换知 ,看
,看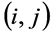 位置有
位置有
 (13)
(13)
此时分两种情形讨论。情形(1)对任意 及任意
及任意 有
有 。
。
由 ,其中
,其中 ,可推出
,可推出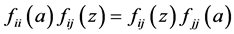 。然后由
。然后由 得
得
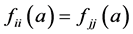 (14)
(14)
由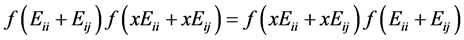 ,看
,看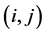 位置可得
位置可得
 (15)
(15)
令 ,由(1)得
,由(1)得
 (16)
(16)
由此情形条件可知
 (17)
(17)
令 ,以下证明对任意
,以下证明对任意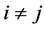 有
有
 (18)
(18)
由(13)可知,当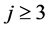 时有,
时有,

又对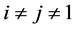 有
有 ,从而得(18)式。
,从而得(18)式。
由 可得
可得 ,从而由(18)得
,从而由(18)得

此时也满足(18)。当 时,又由
时,又由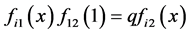 可推出
可推出 ,仍然满足(18)。总之,(18)对所有情形成立。
,仍然满足(18)。总之,(18)对所有情形成立。
令 ,则由(13)计算可得
,则由(13)计算可得 ,则有
,则有

再由
易推出 ,由(13)得
,由(13)得

则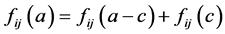 ,从而有
,从而有 ,(17)式意味着
,(17)式意味着 ,故
,故 为
为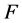 的单自同态。
的单自同态。
令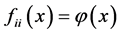 ,则
,则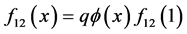 中,
中, 时
时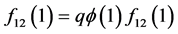 ,则
,则
 (19)
(19)
由(15)得 ,由(19)得
,由(19)得 ,故
,故
 (20)
(20)
由(18),设 ,易见
,易见
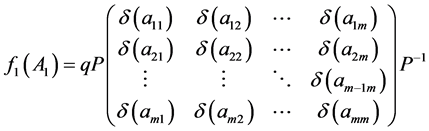
注意到 及(18)式,易见
及(18)式,易见 ,这样结论(ii)的(1)被证明。
,这样结论(ii)的(1)被证明。
情形(2):对某 及某
及某 有
有 。
。
此时由(13)可知 ,设
,设 互不相等,由(13)可知
互不相等,由(13)可知 ,由
,由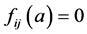 知
知 ,类似的由
,类似的由 有
有 ,接着用类似的方法可证得
,接着用类似的方法可证得 ,
, ,
, ,
, ,此时设
,此时设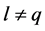 ,由(13)可知
,由(13)可知 ,由
,由 知
知 ,因此
,因此 ,结论(ii)的(2)被证明。
,结论(ii)的(2)被证明。
(iii)充分性
设 ,易证
,易证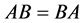 当且仅当
当且仅当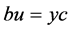 ,
, 和
和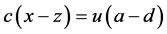 成立。
成立。
由(iii)中(1)可知
 ,
, ,
,
若 其一为0,则有
其一为0,则有 ,即
,即 。
。
若 都不为0,则
都不为0,则
 。
。
又 是自同态,由
是自同态,由 可得
可得 成立。故此时
成立。故此时 依然成立。
依然成立。
由(iii)中(1)可知 ,
,

若 其一为0,则有
其一为0,则有 ,即
,即
若 都不为0,则
都不为0,则
 。又
。又 是自同态,由
是自同态,由 可得
可得 成立,故此时
成立,故此时 依然成立。
依然成立。
同理 成立,故有
成立,故有 ,由(iii)中(2)可知
,由(iii)中(2)可知 ,
, 都为0,显然有
都为0,显然有 ,故充分性成立。
,故充分性成立。
下证必要性若 ,
,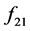 至少其一不为0时,不妨设
至少其一不为0时,不妨设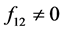 (若
(若 ,证明是类似的)由
,证明是类似的)由 ,其中
,其中 ,
, ,知
,知 ,从而有
,从而有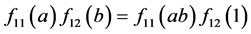 。
。
由(14)令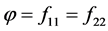 ,则
,则
 (21)
(21)
又由(15)得
 (22)
(22)
综合(21)及(22)得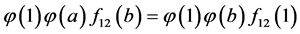 及
及 ,由已知
,由已知 及(21)易见
及(21)易见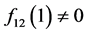 从而得
从而得
 (23)
(23)
于是令 则仿
则仿 的情形易证
的情形易证 为
为 的域自同态。
的域自同态。

对 ,
, 都为0时,仿
都为0时,仿 情形易得
情形易得 ,故(iii)成立。
,故(iii)成立。
注记3.2:如果在定理3.1中去掉 或
或 ,结论如何?这仍然是个开问题。
,结论如何?这仍然是个开问题。
文章引用
闫盼盼,张 隽,曹重光. 关于诱导映射的两个保持问题
Two Preserver Problems on Induced Maps[J]. 理论数学, 2015, 05(05): 247-254. http://dx.doi.org/10.12677/PM.2015.55035
参考文献 (References)
- 1. Li, C.K., Plevnik, L. and Semrl, P. (2012) Preservers of matrix pairs with a fixed inner product value. Operators and Matrices, 6, 433-464. http://dx.doi.org/10.7153/oam-06-29
- 2. Cao, C.G., Ge, Y.L. and Yao, H.M. (2013) Maps preserving classical adjoint of products of two matrices. Linear and Multilinear Algebra, 61, 1593-1604. http://dx.doi.org/10.1080/03081087.2012.753592
- 3. Semrl, P. (2008) Commutativity preserving maps. Linear Algebra and Its Applications, 429, 1051-1070. http://dx.doi.org/10.1016/j.laa.2007.05.006
- 4. Li, C.K., Semrl, P. and Sze, N.S. (2007) Maps preserving the nilpotency of products of operators. Linear Algebra and Its Applications, 424, 222-239. http://dx.doi.org/10.1016/j.laa.2006.11.013
- 5. Chooi, W.L. and Ng, W.S. (2010) On classical adjoint-commuting mappings betweenmatrix algebras 0. Linear Algebra and Its Applications, 432, 2589-2599. http://dx.doi.org/10.1016/j.laa.2009.12.001
- 6. Liu, S.W. and Zhang, G.D. (2006) Maps preserving rank 1 ma-trices over fields. Journal of Natural Science of Heilongjiang University, 23, 138-140.
- 7. Yang, L., Ben, X.Z., Zhang, M. and Cao, C.G. (2014) Induced maps on matrices over fields. Abstract and Applied Analysis, 2014, Article ID: 596796, 5 p.