Pure Mathematics
Vol.06 No.03(2016), Article ID:17543,5
pages
10.12677/PM.2016.63029
Properties of Finite Order Meromorphic Solutions of Two Classes of Nonlinear Difference Equations
Sheng Li, Baoqin Chen
College of Science, Guangdong Ocean University, Zhanjiang Guangdong

Received: Apr. 29th, 2016; accepted: May 10th, 2016; published: May 13th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
This paper is mainly to consider the finite order meromorphic solutions of two classes of nonlinear difference equations. Some results on the properties of the solutions are proved and examples are provided.
Keywords:Difference Equation, Meromorphic Function, Nevanlinna Theory

两类非线性差分方程有限级亚纯解的性质
李升,陈宝琴
广东海洋大学理学院,广东 湛江

收稿日期:2016年4月29日;录用日期:2016年5月10日;发布日期:2016年5月13日

摘 要
本文主要研究两类非线性差分方程的有限级亚纯解,得到了一些关于解的性质,并给出了一些例子。
关键词 :差分方程,亚纯函数,Nevanlinna理论

1. 引言
在下文中,我们将使用Nevanlinna理论 [1] - [3] 的标准记号。设 为亚纯函数,用
为亚纯函数,用 ,
,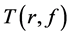 和
和 分别表示
分别表示 的极点计数函数,特征函数和增长级。如果
的极点计数函数,特征函数和增长级。如果 满足
满足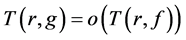 ,则称
,则称 为
为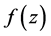 的小函数。用
的小函数。用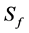 表示
表示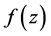 的所有小函数之集,并记由
的所有小函数之集,并记由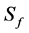 生成的域为
生成的域为 。
。
J. Rieppo在文 [4] 中考虑了差分方程
 , (1)
, (1)
的有限级整函数解,其中 为有限级周期函数函数且
为有限级周期函数函数且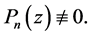 用
用 表示由
表示由 添加元素
添加元素 后所得的域扩张。J. Rieppo证明了以下结果:
后所得的域扩张。J. Rieppo证明了以下结果:
定理1 [4] 设 为有限级整函数且满足方程(1)。如果方程(1)的系数均为以c为周期的有限级整函数,那么或者
为有限级整函数且满足方程(1)。如果方程(1)的系数均为以c为周期的有限级整函数,那么或者 为以c为周期的周期函数,或者
为以c为周期的周期函数,或者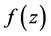 满足关于代数方程:
满足关于代数方程:
 ,(2)
,(2)
其中,方程(2)的系数均属于L。
一个自然的问题是:当 为有限级亚纯函数时,有何结果?考虑这个问题,我们证明了如下结果。
为有限级亚纯函数时,有何结果?考虑这个问题,我们证明了如下结果。
定理2 设 为有限级亚纯函数且满足方程(1)。如果方程(1)的系数均为以c为周期的有限级整函数且
为有限级亚纯函数且满足方程(1)。如果方程(1)的系数均为以c为周期的有限级整函数且 ,那么或者
,那么或者 为以c为周期的周期函数,或者
为以c为周期的周期函数,或者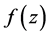 满足关于代数方程(2)其中,方程(2)的系数均属于L。
满足关于代数方程(2)其中,方程(2)的系数均属于L。
我们还考虑了以下形式的差分方程:
 , (3)
, (3)
的有限级整函数解,其中 为有限级周期函数函数且
为有限级周期函数函数且 并得到以下结果:
并得到以下结果:
定理3 设 为有限级亚纯函数且满足方程(1)。如果方程(1)的系数均为以c为周期的有限级整函数且
为有限级亚纯函数且满足方程(1)。如果方程(1)的系数均为以c为周期的有限级整函数且 ,那么或者
,那么或者 为以c为周期的周期函数,或者
为以c为周期的周期函数,或者 满足关于代数方程
满足关于代数方程
 (4)
(4)
其中,方程(4)的系数均属于L。
根据M. Ozawa在文 [5] 中的结果,对任意给定的正数 总存在周期整函数
总存在周期整函数 满足
满足 。下面的例1和例2表明,存在函数满足定理2和定理3的条件。例3和例4则表明条件
。下面的例1和例2表明,存在函数满足定理2和定理3的条件。例3和例4则表明条件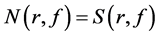 并不是必要的。这将在未来的研究中做进一步的探讨。
并不是必要的。这将在未来的研究中做进一步的探讨。
例1 选取周期为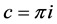 的整函数函数
的整函数函数 ,则函数
,则函数 满足方程
满足方程
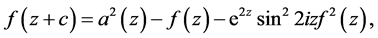
此时, 以
以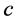 为周期,且
为周期,且 满足
满足 和方程
和方程
例2 选取周期为 的整函数函数
的整函数函数 ,则函数
,则函数 满足方程
满足方程
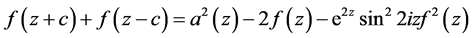 ,
,
此时, 以
以 为周期,且
为周期,且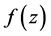 满足
满足 和方程
和方程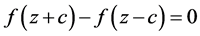 。
。
例3 函数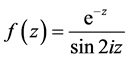 满足方程
满足方程
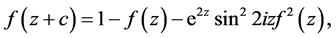
此时, 以
以 为周期,且
为周期,且 满足方程
满足方程 ,但不满足条件
,但不满足条件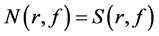 。
。
例4 函数 满足方程
满足方程

此时,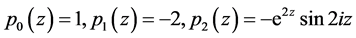 以
以 为周期,且
为周期,且 满足方程
满足方程 但不满足条件
但不满足条件 。
。
2. 引理
引理1 [6] 设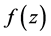 为有限级亚纯函数,则对任意常数c,有
为有限级亚纯函数,则对任意常数c,有
 ,
,
在至多除去一个有限对数测度的集合外成立。
引理2 [7] [8] 设 为有限级亚纯函数,则对任意常数c,有
为有限级亚纯函数,则对任意常数c,有
 ,
,
在至多除去一个有限对数测度的集合外成立。
3. 定理2的证明
不失一般性,假设 ,则由引理1可知
,则由引理1可知
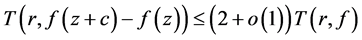 ,
,
在至多除去一个有限对数测度的集合外成立。故 为有限级亚纯函数。
为有限级亚纯函数。
注意到 以
以 为周期,对两边作一次平移运算,可得
为周期,对两边作一次平移运算,可得
 。
。
再结合方程(1)即得,
 。 (5)
。 (5)
对方程(5)两边同时除以 可得
可得
 。
。
进而由定理条件以及引理2可得
 。
。
故存在函数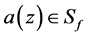 ,使得
,使得 。这就证明了
。这就证明了 满足代数方程
满足代数方程
 ,
,
其中,方程的系数均属于 。
。
4. 定理3的证明
注意到,若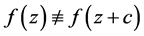 ,则一方面由引理2易得
,则一方面由引理2易得
 。
。
另一方面,由方程(3)可得
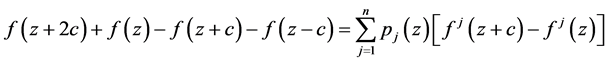 ,
,
进而有
 。
。
由上式,并类似于定理2的证明,即可证明定理3。
致谢
本文得到国家自然科学基金项目(No. 11526057)和广东省自然科学基金项目(No. 2015A030313620)的资助。
文章引用
李 升,陈宝琴. 两类非线性差分方程有限级亚纯解的性质
Properties of Finite Order Meromorphic Solutions of Two Classes of Nonlinear Difference Equations[J]. 理论数学, 2016, 06(03): 190-194. http://dx.doi.org/10.12677/PM.2016.63029
参考文献 (References)
- 1. Hayman, W. (1964) Meromorphic Functions. Clarendon Press, Oxford.
- 2. Laine, I. (1993) Nevanlinna Theory and Complex Differential Equations. W. de Gruyter, Berlin. http://dx.doi.org/10.1515/9783110863147
- 3. 杨乐. 值分布论及其新研究[M]. 北京: 科学出版社, 1982.
- 4. Rieppo, J. (2015) Malmquist-Type Results for Difference Equations with Periodic Coefficients. Computa-tional Methods and Function Theory, 15, 449-457. http://dx.doi.org/10.1007/s40315-015-0109-z
- 5. Ozawa, M. (1978) On the Existence of Prime Periodic Entire Functions. Kodai Mathematical Seminar Reports, 29, 308-321. http://dx.doi.org/10.2996/kmj/1138833654
- 6. Halburd, R.G. and Korhonen, R.J. (2007) Finite-Order Mero-morphic Solutions and the Discrete Painlevé Equations. Proceedings of the London Mathematical Society, 94, 443-474. http://dx.doi.org/10.1112/plms/pdl012
- 7. Chiang, Y.M. and Feng, S.J. (2009) On the Growth of Logarithmic Differences, Difference Quotients and Logarithmic Derivatives of Meromorphic Functions. Transactions of the American Mathematical Society, 7, 3767-3791. http://dx.doi.org/10.1090/S0002-9947-09-04663-7
- 8. Halburd, R.G. and Korhonen, R.J. (2006) Nevanlinna Theory for the Difference Operator. Annales Academiæ Scientiarum Fennicæ Mathematica, 31, 463-478.