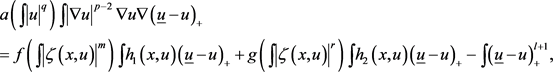Pure Mathematics
Vol.
09
No.
03
(
2019
), Article ID:
30136
,
8
pages
10.12677/PM.2019.93041
Existence of Solution for One Class of p-Laplacian Problem
Lei Li
Department of Mathematics and Statistics, Guangxi Normal University, Guilin Guangxi
Received: Apr. 16th, 2019; accepted: Apr. 27th, 2019; published: May 9th, 2019

ABSTRACT
In this paper, we study the existence of weak solutions for the Dirichlet problems for one class of nonlinear p-Laplacian equations. Our proof combines the presence of sub and supersolution with the pseudomonotone operators theory.
Keywords:Sub and Supersolution, Pseudomonotone Operators Theory, p-Laplacian Equations
一类p-Laplace方程解的存在性问题
李磊
广西师范大学,数学与统计学院,广西 桂林
收稿日期:2019年4月16日;录用日期:2019年4月27日;发布日期:2019年5月9日

摘 要
本文利用上下解与伪单调算子方法讨论一类p-Laplace方程的Dirichlet问题解的存在性问题。
关键词 :上下解,伪单调算子,p-Laplace

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
因为含p-Laplace算子
的微分方程的边值问题在非牛顿力学、宇宙物理、血浆问题和弹性理论等诸多领域有着广泛的应用,所以对此类问题的研究吸引了很多学者的目光。
本文考虑一类具有p-Laplace算子方程的Dirichlet边值问题:
(1)
解的存在性。该方程满足下列假设:
(H1)
,是一个有界的区域且边界光滑。
(H2)
。
(H3)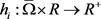 是连续的函数。
是连续的函数。
(H4)
是连续的函数且
。
(H5)
。
解的存在性问题一直是偏微分方程研究中的重要课题,注意到p = 2时,方程(1)化为一类含有Laplace算子的边值问题:
(2)
文 [1] 在满足H1~H5的假设条件下,使用上下解与伪单调算子的方法证明方程(2)至少存在一个解。
在偏微分方程理论中,解的存在性与不存在性都与所选取的函数空间有关,本文所选取的函数空间是依赖于参数p的,其中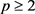 。之所以这样做是为了使结果具有一般性。需要强调的是,方程(1)、方程(2)所选取的函数空间是不同的。由文 [1] 知,方程(2)选取的函数空间是
并且证明了解存在且解
。本文选取的函数空间是
,本文的目的在于使用上下解与伪单调算子方法证明方程(1)的解存在且解
。之所以这样做是为了使结果具有一般性。需要强调的是,方程(1)、方程(2)所选取的函数空间是不同的。由文 [1] 知,方程(2)选取的函数空间是
并且证明了解存在且解
。本文选取的函数空间是
,本文的目的在于使用上下解与伪单调算子方法证明方程(1)的解存在且解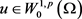 。此外,由于p-Laplace算子的非线性性,对比于
的特殊情形解的存在性
。此外,由于p-Laplace算子的非线性性,对比于
的特殊情形解的存在性
结果的建立需要更精细的讨论。本文将得到与文 [1]
情形相一致的结果 (本文规定 )
本文所得的结果是:
定理1 在满足(H1~H5)的假设下,假设方程(1)存在上下解
并且满足下列条件:
(3)
(4)
(5)
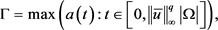 (6)
(6)
那么对于所有的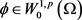 ,方程(1)至少存在一个解
使得:
,方程(1)至少存在一个解
使得:
(7)
成立并且满足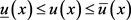 。
。
2. 预备知识
为证明定理1我们先做一些必要准备。
定义2.1 (见文献 [2] [3] )称算子
a) 是有界算子,如果
,
是
中的有界凸集。
b) 是强制算子,如果满足
(8)
c) 是伪单调算子,如果满足
在
中,且
(9)
则对任意的
,有
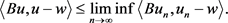 (10)
(10)
引理2.2 (Brezis) (见文献 [4] )算子
是伪单调的,有界的,强制的。X是实自反的可分的Banach空间,则对于任意的
,方程
存在解
。
定义2.3 (见文献 [5] )设X是一个
空间,
。称
弱收敛到x,记做
,是指:对于
都有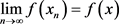 。这时x称做点列
。这时x称做点列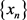 的弱极限。
的弱极限。
引理2.4 设
,若对每一个
(q为p的共轭数),当
时,有
,则称
弱收敛于f。
证明:因为
,可令
,那么
,再由定义2.3知
弱收敛于f。
定义2.5 (见文献 [5] )设X是
空间,
。称
弱收敛到f记做
,是指:对于
,都有
。这时f称做泛函序列
的*弱极限。
定义2.6 (见文献 [6] )设X是一个赋范空间,如果在典型映射的意义下
,则称空间X是自反的。
引理2.7 (见文献 [5] )当X是一个自反空间时,*弱收敛与弱收敛等价。
引理2.8 (见文献 [7] )对任意
下面不等式成立:
(11)
引理2.9 (见文献 [8] ) (Holder不等式)设
,
。若
,则
,并且
。
3. 定理1的证明
第一步,构造修正问题:
定义截断函数:
令:
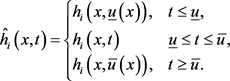
因为
是连续的函数,所以可令
,再由
的定义易得:
。
定义函数:
(12)
其中,
。
再定义修正函数:
。
利用上述函数我们研究下列Dirichlet问题:
(13)
第二步,对H作出估计:
在
时:
,此时,对方程(13)用最值原理易得:
,因此:
(14)
在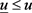 时:
时:
(15)
第三步,证明
:
已知
,显然有
。
令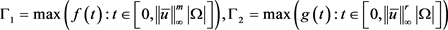 ,利用上述条件以及Minkowski不等式我们有:
,利用上述条件以及Minkowski不等式我们有:
所以有
,且与u的选取无关。
第四步,作算子:
。
(16)
对任意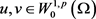 。
。
第五步,证明B是有界的:
已知
,
(17)
其中,
,那么由上式知B是有界的。
第六步,证明B是强制的:
当
时,则
因此,B是强制的。
第七步,证明B是一个伪单调算子:
根据定义(2.1)就是证明如果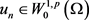 且
并且:
且
并且:
(18)
那么有:
(19)
已知
且
,又由第三步知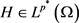 ,与
,与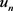 选取无关且
选取无关且 ,根据引理(2.4)得:
,根据引理(2.4)得:

又已知
因此
(20)
根据弱收敛的定义(2.3)可得:
类似可以证明:
(21)
联合(20),(21)两式可得:
(22)
进而得出:
(23)
所以有:
。
由(22),(23)易知:
(24)
又已知
是自反空间联合引理(2.7)可得:
(25)
这就证明了B是伪单调算子。
所以B是有界的、强制的、伪单调的,根据引理(2.2)可知方程(13)有解已经证明。
第八步,我们证明方程(1)有解:
即证明
。
先令
,
进而有:
因此,
对(4)分步积分可得:
,
所以,
又由(11)知,
,进而有:
。
再令
,
进而有:
又由前面的
和 的定义得到:
的定义得到:
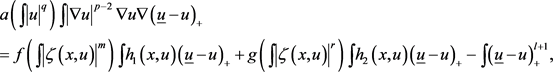
对(5)分步积分得:
(26)
进而有:
进而可得,
。
综上,
。
因此,定理1得证。
文章引用
李 磊. 一类p-Laplace方程解的存在性问题
Existence of Solution for One Class of p-Laplacian Problem[J]. 理论数学, 2019, 09(03): 308-315. https://doi.org/10.12677/PM.2019.93041
参考文献
- 1. Alves, C.O. and Covei, D.P. (2015) Existence of Solution for a Class of Nonlocal Elliptic Problem via Sub-Supersolution Method. Nonlinear Analysis Real World Applications, 23, 1-8.
https://doi.org/10.1016/j.nonrwa.2014.11.003
- 2. Zeidler, E. (1991) Nonlinear Functional Analysis and Its Applications, Part I: Fixed-Point Theorems. Acta Applicandae Mathematica, 24, 312-314.
- 3. 李开泰, 马逸尘. 数学物理方程Hilbert空间方法[M]. 北京: 科学出版社, 2008.
- 4. Troianiello, G.M. (2010) Elliptic Differential Equations and Obstacle Problems. University Series in Mathematics. Springer US, New York.
- 5. 张恭庆, 林源渠. 泛函分析讲义[M]. 北京: 北京大学出版社, 1987.
- 6. 孙炯, 王万义, 郝建文. 泛函分析[M]. 北京: 高等教育出版社, 2010.
- 7. Peral, I. (2010) Multiplicity of Solutions for the p-Laplacian. http://matematicas.uam.es/~ireneo.peral/ICTP.pdf
- 8. 王明新. 索伯列夫空间[M]. 北京: 高等教育出版社, 2013.





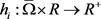 是连续的函数。
是连续的函数。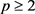 。之所以这样做是为了使结果具有一般性。需要强调的是,方程(1)、方程(2)所选取的函数空间是不同的。由文 [1] 知,方程(2)选取的函数空间是
并且证明了解存在且解
。本文选取的函数空间是
,本文的目的在于使用上下解与伪单调算子方法证明方程(1)的解存在且解
。之所以这样做是为了使结果具有一般性。需要强调的是,方程(1)、方程(2)所选取的函数空间是不同的。由文 [1] 知,方程(2)选取的函数空间是
并且证明了解存在且解
。本文选取的函数空间是
,本文的目的在于使用上下解与伪单调算子方法证明方程(1)的解存在且解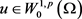 。此外,由于p-Laplace算子的非线性性,对比于
的特殊情形解的存在性
。此外,由于p-Laplace算子的非线性性,对比于
的特殊情形解的存在性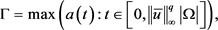 (6)
(6)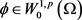 ,方程(1)至少存在一个解
使得:
,方程(1)至少存在一个解
使得: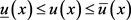 。
。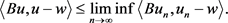 (10)
(10)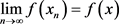 。这时x称做点列
。这时x称做点列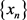 的弱极限。
的弱极限。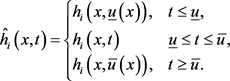
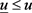 时:
时: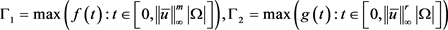 ,利用上述条件以及Minkowski不等式我们有:
,利用上述条件以及Minkowski不等式我们有: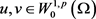 。
。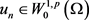 且
并且:
且
并且: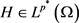 ,与
,与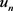 选取无关且
选取无关且 ,根据引理(2.4)得:
,根据引理(2.4)得:
 的定义得到:
的定义得到: