Modeling and Simulation
Vol.05 No.04(2016), Article ID:19104,7
pages
10.12677/MOS.2016.54025
Principal Basis Analysis and Application in Feature Selection of Water Quality Data
Hui Zou1,2, Zhihong Zou1*, Xiaojing Wang1
1School of Economics and Management, Beihang University, Beijing
2School of Science, China Agricultural University, Beijing

Received: Nov. 11th, 2016; accepted: Nov. 27th, 2016; published: Nov. 30th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
With the increasing emphasis on the environment and the improvement of monitoring technology, there appear more and more multivariate data in which the variable sets have multi-collinearity problem. The water quality data of Taizi River belong to this kind of data. In order to avoid the limitation of the traditional method, the principal basis analysis method based on the Gram- Schmidt transform is used to the feature selection of the water quality data of the Taizi River. This method selects information effectively from the large-scale variable set with the minimal loss of original information. Meanwhile, this method can exclude all redundant variables and reduplicate information. Furthermore, it can obtain a mini-dimensional orthogonal basis. Using the measurement of the net information content ratio of the selected features, it is effective to select the representative water quality monitoring variables. It is conducive to the improvement of water quality monitoring work and the experimental results indicate the effectiveness of this method.
Keywords:Gram-Schmidt Transform, Principal Basis, Variable Selection

主基底分析方法及在水质监测指标 筛选中的研究
邹辉1,2,邹志红1*,王晓静1
1北京航空航天大学经济管理学院,北京
2中国农业大学理学院,北京

收稿日期:2016年11月11日;录用日期:2016年11月27日;发布日期:2016年11月30日

摘 要
随着人们对环境的日益重视和监测技术的提高,水质监测中出现了越来越多变量相关的多变量数据。其中,太子河水质数据属于数据相关的多变量数据。由于传统方法的局限性,本文利用基于Gram-Schmidt变换的主基底分析方法进行太子河水质数据的监测指标筛选工作。这种方法能够在原数据信息损失尽可能小的前提下,排除所有的冗余变量以及变量集合中的重叠信息,有效地对大规模变量集中的信息进行筛选,从而得到一个标准正交的主基底。并且,通过对所选基底的“净信息含量比”的测度,可以有效地选择具有代表性的水质监测变量。有利于对水质监测工作进行科学合理的改进。数值实验表明,使用Gram-Schmidt变换的主基底分析方法对太子河水质数据进行分析是有效的。
关键词 :Gram-Schmidt变换,主基底,变量筛选

1. 引言
在许多研究领域的建模与数据处理工作中,为了不遗漏重要的信息,研究人员往往倾向于选择数量较多的初始变量。这样形成的数据集具有高维度,变量中的冗余信息较多。很多时候自变量集合中包含严重的多重相关性,如果直接采用所有这些变量进行建模,还将对分析结论造成不良影响。很多的多元统计方法比如多元线性回归、Fisher判别、聚类分析等都具有变量筛选的功能。然而从理论上看,当变量集合中存在严重的多重相关性时,这些方法的计算精度都会受到影响。在数据降维方面也有许多非常经典的方法,例如主成分分析、因子分析、典型相关分析等。已经被广泛应用于环境问题中高维数据的降维和分类 [1] - [8] 。这些方法的共同特点是依照某种最优化原则,在原变量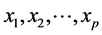 中提取成分
中提取成分 ,然后再利用这些成分进行相关的分析工作。但是,由于每一个成分都是原始变量的线性组合,所以这些方法都没有变量筛选的功能。一个突破性的研究进展是文献 [9] 提出的改良主成分分析方法。该方法通过变量筛选,找到原始变量集合的一个子集,使得筛选后的变量尽可能地在表现主成分的结构方面与原变量有很相似的效果。此外,一种简便可靠的基于Gram Schmidt过程的主基底分析方法被提出来并应用于指标筛选 [10] 。该方法可以消除重叠信息的所有冗余变量,在信息的损失降低到最少的前提下,得到一组正交基,可以更有效地进行变量筛选。
,然后再利用这些成分进行相关的分析工作。但是,由于每一个成分都是原始变量的线性组合,所以这些方法都没有变量筛选的功能。一个突破性的研究进展是文献 [9] 提出的改良主成分分析方法。该方法通过变量筛选,找到原始变量集合的一个子集,使得筛选后的变量尽可能地在表现主成分的结构方面与原变量有很相似的效果。此外,一种简便可靠的基于Gram Schmidt过程的主基底分析方法被提出来并应用于指标筛选 [10] 。该方法可以消除重叠信息的所有冗余变量,在信息的损失降低到最少的前提下,得到一组正交基,可以更有效地进行变量筛选。
本文中,将应用这种方法进行太子河水质数据的指标筛选,更有效地选择具有代表性的变量。
2. 基于Gram-Schmidt变换的变量筛选方法
2.1. 主基底分析方法
用于指标筛选的主基底分析方法就是基于主成分分析的Gram-Schmidt过程 [10] 。它的原理如下:
定义1:记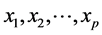 是秩为
是秩为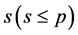 的向量集,
的向量集,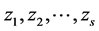 是经过Gram-Schmidt过程后得到的正交向量。如果满足条件
是经过Gram-Schmidt过程后得到的正交向量。如果满足条件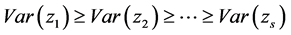 ,并且
,并且 达到最大值,则
达到最大值,则 就是相应于原始变量的主基底。
就是相应于原始变量的主基底。
从Gram-Schmidt过程和定义1得到,最大方差法可以被用于得到一组变量的主基底,具体计算过程如下:
1) 对向量 进行标准化;
进行标准化;
2) 令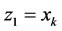 ,要求满足
,要求满足
 (1)
(1)
不妨假设 ,那么
,那么 ;
;
3) 对于剩下的变量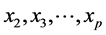 ,继续分别和
,继续分别和 进行Gram-Schmidt变换,得到一组相应的变量:
进行Gram-Schmidt变换,得到一组相应的变量:
 (2)
(2)
4) 对于 ,选择这组变量中方差最大的一个记为
,选择这组变量中方差最大的一个记为 ,that is
,that is
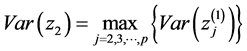 (3)
(3)
不妨假设 ,也就是
,也就是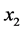 是第二个进行Gram-Schmidt变换的向量;
是第二个进行Gram-Schmidt变换的向量;
5) 对于剩下的变量 ,分别和
,分别和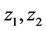 进行Gram-Schmidt变换。得到一组相应的变量:
进行Gram-Schmidt变换。得到一组相应的变量:
 (4)
(4)
6) 对于 ,选择具有最大方差的变量记为
,选择具有最大方差的变量记为 ,即
,即
 (5)
(5)
7) 重复以上的过程,得到一组相互正交的向量 。
。
根据主基底中信息量的特点,下面给出净信息总量和净信息含量比的概念:
定义2: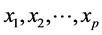 是秩为
是秩为 的一组向量。经过Gram-Schmidt变换后得到主基底
的一组向量。经过Gram-Schmidt变换后得到主基底 ,主基底的信息总量
,主基底的信息总量 就是原始向量
就是原始向量 的信息总量。
的信息总量。
定义3:对任意的 ,定义它所携带的“净信息含量比”为
,定义它所携带的“净信息含量比”为
 (6)
(6)
根据累计的净信息含量比,就可以最终确定在应用分析中所需要的主基底的维数。
2.2. 主基底分析和主成分分析的比较
设原始变量集合为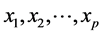 ,则该数据集合的总信息量为
,则该数据集合的总信息量为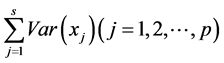 ,经主成分分析计算后得到的主成分集合为
,经主成分分析计算后得到的主成分集合为 ,并且有
,并且有 。如果最终保留了m个成分,则原始变量的总信息量被分解为两个部分,这可以表达为
。如果最终保留了m个成分,则原始变量的总信息量被分解为两个部分,这可以表达为
 (7)
(7)
其中, 为保留的信息;
为保留的信息; 为被删除的信息。
为被删除的信息。
由于有 ,所以很显然,主成分分析不能解决变量筛选的问题。而且,变量之间的多重相关性和冗余信息还会对主成分分析的计算结论产生重要的影响。
,所以很显然,主成分分析不能解决变量筛选的问题。而且,变量之间的多重相关性和冗余信息还会对主成分分析的计算结论产生重要的影响。
与之相反,主基底分析中的信息分解与选择则采用了完全不同的一种形式。对于一组秩为 的变量集合
的变量集合 ,经过主基底分析后,得到s个主基底变量
,经过主基底分析后,得到s个主基底变量 。为了记号方便起见,这里不妨设与
。为了记号方便起见,这里不妨设与 对应的关联变量分别为
对应的关联变量分别为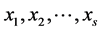 。于是,其信息分解方式可以表达为
。于是,其信息分解方式可以表达为
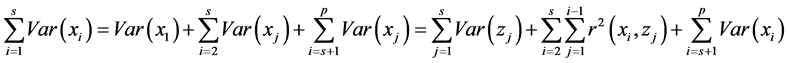
其中, 为保留信息,也为全部的净信息;
为保留信息,也为全部的净信息; 为被删除变量的信息。特别值得关注的部分是
为被删除变量的信息。特别值得关注的部分是 ,这里是在由
,这里是在由 得到
得到 的过程中,逐渐被剥离的重叠信息的总和。式(19)说明,通过Gram-Schmidt过程不但可以完整地删除所有的冗余变量,而且还可以有效地拆分和去除
的过程中,逐渐被剥离的重叠信息的总和。式(19)说明,通过Gram-Schmidt过程不但可以完整地删除所有的冗余变量,而且还可以有效地拆分和去除 之间多重相关性的冗余信息。
之间多重相关性的冗余信息。
3. 案例研究
3.1. 研究区域及数据
太子河发源于抚顺,全长约413 km,流域面积约13,883 km2。太子河辽阳段位于太子河中游,经本溪市进入辽阳市境内,入口与参窝水库相接,出口进入鞍山境内,境内流程142.8 km,流域面积约4000 km2,约占全市总面积的85%。太子河辽阳段及其支流汤河、北沙河和柳壕河与参窝水库和汤河水库构成了辽阳地表水监测体系。太子河辽阳段干流上共设有3个监测断面,分别为入市断面参窝坝下断面、国控断面下王家桥断面和出市断面下口子断面。本文采用太子河流域的一个监测点参窝坝下2012年月度监测数据,选取了13个变量, ——流量(m3/s),
——流量(m3/s),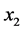 ——水温(℃),
——水温(℃), ——pH,
——pH, ——电导率(MS/m),
——电导率(MS/m), ——溶解氧(mg/l),
——溶解氧(mg/l), ——高锰酸盐指数(mg/l),
——高锰酸盐指数(mg/l), ——五日生化需氧量(mg/l),
——五日生化需氧量(mg/l), ——氨氮(mg/l),
——氨氮(mg/l),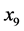 ——石油类(mg/l),
——石油类(mg/l), ——挥发酚(mg/l),
——挥发酚(mg/l),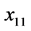 ——总磷(mg/l),
——总磷(mg/l), ——氟化物(mg/l),
——氟化物(mg/l), ——阴离子表面活化剂(mg/l)。原始数据见表1。
——阴离子表面活化剂(mg/l)。原始数据见表1。
3.2. 水质监测指标的筛选
将主基底分析方法应用于太子河的水质数据,进行监测指标的筛选。
首先,对于原始变量做标准化处理,之后,选取 ,使得
,使得

从表2中对应的最大数值可知,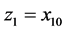 。
。
通过计算这13个变量的相关系数矩阵,可以发现,在自变量集合间存在非常严重多重相关性。
然后分别将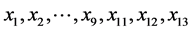 与
与 做Gram-Schmidt变换,并计算
做Gram-Schmidt变换,并计算 的方差,见表3。由表3中对应的最大数值可知,
的方差,见表3。由表3中对应的最大数值可知, ,所以
,所以 是主基底采用的第2个变量。重复以上过程,直到所有的变量都经过Gram-Schmidt变换变成相互正交的变量。
是主基底采用的第2个变量。重复以上过程,直到所有的变量都经过Gram-Schmidt变换变成相互正交的变量。
Table 1. Original data
表1. 原始数据表
Table 2. Values of
表2. 的数值
的数值
Table 3. Variance of
表3. 的方差
的方差
计算每个变量的净信息含量 ,得到主基底中各维变量
,得到主基底中各维变量 的净信息含量比
的净信息含量比 (见表4)。该表的第1行中,括号内的变量为各个
(见表4)。该表的第1行中,括号内的变量为各个 所对应的原始变量。
所对应的原始变量。
由表4得到的各变量累计净信息含量比,见图1可见,经过Gram-Schmidt正交变换后,
 的累积净信息含量比达到96.096%。所以在太子河水质数据的研究中,选取8个原变量
的累积净信息含量比达到96.096%。所以在太子河水质数据的研究中,选取8个原变量 ——挥发酚(毫克/升),
——挥发酚(毫克/升), ——pH,
——pH, ——石油类(毫克/升),
——石油类(毫克/升),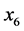 ——高锰酸盐指数(毫克/升),
——高锰酸盐指数(毫克/升), ——阴离子表面活化剂(毫克/升),
——阴离子表面活化剂(毫克/升), ——氨氮(毫克/升),
——氨氮(毫克/升), ——流量(m3/s),
——流量(m3/s), ——电导率(MS/m),
——电导率(MS/m),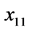 ——总磷(毫克/升),便可以96.096%的精度代表所有原变量集合中的净信息量。
——总磷(毫克/升),便可以96.096%的精度代表所有原变量集合中的净信息量。
Table 4. RNI of variables
表4. 每个变量的RNI值

Figure 1. The cumulative net information content ratio
图1. 累计净信息含量比
4. 结论
在实际工作中,数据分析人员往往要面对变量数目庞大的数据.本文利用基于Gram-Schmidt变换的一种主基底分析方法进行太子河水质数据的监测指标筛选工作。有效地利用主基底分析方法对大规模变量集中的信息进行筛选,并且通过对所选基底的“净信息含量比”的测度从13个监测指标中选择具有代表性的8个水质监测变量。有利于对水质监测工作进行科学合理的改进。
基金项目
国家自然科学基金(No. 51478025)资助。
文章引用
邹辉,邹志红,王晓静. 主基底分析方法及在水质监测指标筛选中的研究
Principal Basis Analysis and Application in Feature Selection of Water Quality Data[J]. 建模与仿真, 2016, 05(04): 198-204. http://dx.doi.org/10.12677/MOS.2016.54025
参考文献 (References)
- 1. Shrestha, S. and Kazama, F. (2007) Assessment of Surface Water Quality Using Multivariate Statistical Techniques: A Case Study of the Fuji River Basin, Japan. Environmental Modelling & Software, 22, 464-475. http://dx.doi.org/10.1016/j.envsoft.2006.02.001
- 2. Kowalkowski, T., Zbytniewski, R., et al. (2006) Application of Chemo-metrics in River Water Classification. Water Research, 40, 744-752. http://dx.doi.org/10.1016/j.watres.2005.11.042
- 3. Wang, X., Lu, Y., et al. (2007) Identification of Anthropogenic Influences on Water Quality of Rivers in Taihu Watershed. Journal of Envi-ronmental Sciences, 19, 475-481. http://dx.doi.org/10.1016/S1001-0742(07)60080-1
- 4. Juahir, H., Zain, S.M., et al. (2011) Spatial Water Quality Assessment of Langat River Basin (Malaysia) Using Environmetric Techniques. Environmental Monitoring and Assessment, 173, 625-641. http://dx.doi.org/10.1007/s10661-010-1411-x
- 5. Venkatesharaju, K., Somashekar, R.K., et al. (2010) Study of Seasonal and Spatial Variation in Surface Water Quality of Cauvery River Stretch in Karnataka. Journal of Ecology and the Natural Environment, 2, 1-9.
- 6. Singh, K.P., Malik, A., et al. (2005) Water Quality Assessment and Apportionment of Pollution Sources of Gomti River (India) Using Multivariate Statistical Techniques—A Case Study. Analytica Chimica Acta, 538, 355-374. http://dx.doi.org/10.1016/j.aca.2005.02.006
- 7. Zhou, F., Liu, Y., et al. (2007) Application of Multivariate Statistical Methods to Water Quality Assessment of the Watercourses in Northwestern New Territories, Hong Kong. Environmental Monitoring and As-sessment, 132, 1-13. http://dx.doi.org/10.1007/s10661-006-9497-x
- 8. Wang, Y., Liu, C., et al. (2013) Spatial Pattern Assessment of River Water Quality: Implications of Reducing the Number of Monitoring Stations and Chemical Parameters. Environmental Monitoring and Assessment, 186, 1781- 1792. http://dx.doi.org/10.1007/s10661-013-3492-9
- 9. Tanaka, Y. and Mori, Y. (1997) Principal Component Analysis Based on a Subset of Variables: Variable Selection and Sensitivity Analysis. American Journal of Mathematical and Management Sciences, 17, 61-89. http://dx.doi.org/10.1080/01966324.1997.10737430
- 10. 王惠文, 仪彬, 叶明. 基于主基底分析的变量筛选[J]. 北京航空航天大学学报, 2008, 34(11): 1288-1291.
