Advances in Applied Mathematics
Vol.03 No.02(2014), Article ID:13605,7
pages
10.12677/AAM.2014.32018
Extinction for a Class of p-Laplace Evolution Equation with Nonlocal Sources
Haixing Zhang1*, Ruiya Hao1, Juanjuan Shen1, Shuanglong Gan1, Lang Chen2
1School of Sciences, Nantong University, Nantong
2School of Xinglin, Nantong University, Nantong
Email: *13020004@yjs.ntu.edu.cn, 13020005@yjs.ntu.edu.cn
Received: Mar. 5th, 2014; revised: Apr. 1st, 2014; accepted: Apr. 8th, 2014
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this article, the authors establish conditions for the extinction of nonlocal solutions, in finite time, of a class of evolution p-Laplace equation  with
with , in a bounded domain
, in a bounded domain  with
with .
.
Keywords:Fast Diffusion System, Extinction in Finite Time, Nonlinear Sources

带非局部源的p-Laplace发展方程解的熄灭
张海星1*,郝瑞亚1,沈娟娟1,甘双龙1,陈浪2
1南通大学理学院,南通
2南通大学杏林学院,南通
Email: *13020004@yjs.ntu.edu.cn, 13020005@yjs.ntu.edu.cn
收稿日期:2014年3月5日;修回日期:2014年4月1日;录用日期:2014年4月8日

摘 要
本文研究了一类非局部p-Laplace方程
 在一个有界域
在一个有界域
 解的熄灭条件。
解的熄灭条件。
关键词 :快速扩散系统,有限时间熄灭,非局部源

1. 引言
自然界中,在生物进化、物质燃烧等过程中,在诸如死亡速率较快、物质对热量的吸收较强等因素的作用下,进化或燃烧过程可能将无法延续下去,也就是说在某个时刻这种生物将灭绝、燃烧将停止。这种现象在数学意义上,我们就说用来模拟这些扩散运动的模型的解在有限时刻熄灭。
本文研究如下p-Laplace方程
 (1)
(1)
非负解的熄灭性质,其中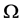 是
是 中的有界域,具有光滑边界
中的有界域,具有光滑边界 均为正常数,
均为正常数,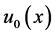 是非负连续函数。
是非负连续函数。
所谓熄灭,即存在一个有限时间 ,使得解在
,使得解在 时非平凡,但对所有的
时非平凡,但对所有的 ,有
,有 。这时
。这时 被称为熄灭时间。
被称为熄灭时间。
关于解的熄灭问题,自从1974年Kalashnikov在文献 [1] 中研究了如下Cauchy问题

并提出了解的熄灭概念以后,许多的数学工作者对熄灭问题产生了兴趣,其中在文献 [2] - [4] 中Lair和Oxley等先后研究了如下形式的非线性扩散方程
 (2)
(2)
证明了问题(2)的解熄灭的充分条件为(对某个 )
)

对于如下的带吸收项的多孔介质方程

它的解的熄灭的充要条件是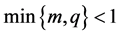 ,也就是说在强吸收
,也就是说在强吸收 ,或者快速扩散
,或者快速扩散 的情况下,问题的解才可能在有限时间熄灭。
的情况下,问题的解才可能在有限时间熄灭。
同样的,对于扩散系数对未知函数具有依赖性的方程,如发展的p-Laplace方程
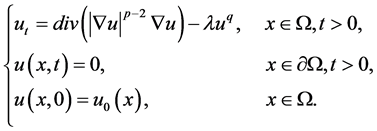 (3)
(3)
顾永耕在文献 [5] 中证明了仅在 或者
或者 时,(3)的解在有限时间熄灭,对于问题(3)中
时,(3)的解在有限时间熄灭,对于问题(3)中 的情况,Dibenedetto和袁洪君等论证了(3)的解在
的情况,Dibenedetto和袁洪君等论证了(3)的解在 时熄灭,而在
时熄灭,而在 时具有正性,即解不会在有限时间熄灭。
时具有正性,即解不会在有限时间熄灭。
从上述的例子中我们可以归纳出,这几类非线性扩散方程在扩散、吸收或者二者耦合作用达到一定强度的情形下解会在某个有限时间熄灭。那么对于具有源的问题,解的熄灭现象能发生的条件就变复杂了。由于源的存在必定阻碍着熄灭现象的发生,则源和扩散项间呈“竞争”关系,而这种“竞争”的结果造成了解的不同性态。下面以具有源的多孔介质方程为例
 (4)
(4)
众所周知,在 或者
或者 且
且 的情况下,问题(4)的解可能在有限时间爆破。然而,最近李玉祥等在文献 [6] 中证明了在
的情况下,问题(4)的解可能在有限时间爆破。然而,最近李玉祥等在文献 [6] 中证明了在 的情形下,仅当
的情形下,仅当 或者
或者 且
且 时(这儿
时(这儿 是算子
是算子 的第一特征值),解有可能在有限时间熄灭。
的第一特征值),解有可能在有限时间熄灭。
反应项带有局部和非局部形式的抛物问题已经被广泛研究,但是绝大部分研究的都是解的爆破性质,如王明新等( [7] )研究下列问题

得到了解整体存在和爆破的条件。在文章 [8] 中,林支桂研究了某类具有非局部源和非局部边界条件的爆破模式。陈玉娟在( [9] )研究了如下问题

也得到解的整体存在性和爆破性质。
对于含有非局部源的解的熄灭,Fang等在 [10] 中研究了如下抛物型问题:

Han等在 [11] 中研究了
 (5)
(5)
并且得到如果在 时,如果
时,如果 ,当初值充分小时,问题(5)的唯一解熄灭,如果
,当初值充分小时,问题(5)的唯一解熄灭,如果 ,问题(5)的最大解是正的,即解不会熄灭,如果
,问题(5)的最大解是正的,即解不会熄灭,如果 解是否熄灭不与第一特征值
解是否熄灭不与第一特征值 有关,而与
有关,而与 有关,其中
有关,其中 是如下椭圆问题
是如下椭圆问题

的唯一正解。
本文的目的在于得到(1)弱解熄灭的充分条件,包括熄灭时间的估计,解的衰减估计等。下面给出弱解的定义,为方便起见,定义 。
。
定义1.1:称非负函数 是问题(1)的在
是问题(1)的在 上的一个解,当且仅当
上的一个解,当且仅当 ,
, ,且对任意的
,且对任意的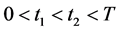 都有
都有
 (6)
(6)
以及

这里,检验函数 。
。
同样可定义问题(1)的一个上(下解) ,我们只要在
,我们只要在 中,
中,
 ,在
,在 上,
上, ,以及对所有的
,以及对所有的 ,在(6)中用
,在(6)中用 代替等号。
代替等号。
本文的主要结论如下:
定理1.1:如果 ,且初值适当小,则(1)的非负弱解在有限时刻熄灭,且如果
,且初值适当小,则(1)的非负弱解在有限时刻熄灭,且如果 则
则
 (7)
(7)
如果 ,令
,令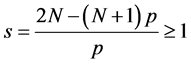 ,则
,则
 (8)
(8)
其中 分别由(14),(17)定义,
分别由(14),(17)定义, 分别由(15),(18)定义。
分别由(15),(18)定义。
2. 定理1.1的证明
定理的证明需用到下面引理,具体证明参阅文献[12] 。
引理2.1:设 分别为(1)的下解和上解,则对几乎所有的
分别为(1)的下解和上解,则对几乎所有的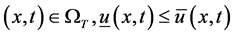 。
。
定理1.1的证明,在(1)两边同时乘以 ,并在Ω上积分,得到
,并在Ω上积分,得到
 (9)
(9)
令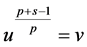 ,则有
,则有

即

则(9)可写成为
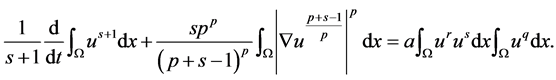 (10)
(10)
下面分两种情况讨论(1) 和(2)
和(2)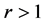 或者
或者 讨论。
讨论。
1) 在第一种情况下,对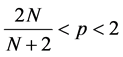 在(10)中取
在(10)中取 ,因为
,因为 ,由
,由 不等式以及Sobolev嵌入定理,我们有
不等式以及Sobolev嵌入定理,我们有
 (11)
(11)
这儿 是嵌入常数,仅依赖于
是嵌入常数,仅依赖于 和
和 。由(10)和(11),我们可得到微分不等式
。由(10)和(11),我们可得到微分不等式

因为 分别对
分别对 用
用 不等式,我们得到
不等式,我们得到

也就是说

由于 ,故可以选择
,故可以选择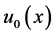 足够小,以满足
足够小,以满足
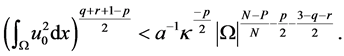 (12)
(12)
则
 (13)
(13)
其中
 (14)
(14)
将(13)积分,得到
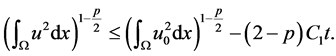
这意味着

所以 在有限时间
在有限时间
 (15)
(15)
熄灭,且(7)成立。
如果 ,在(9)中令
,在(9)中令 ,利用
,利用 不等式和
不等式和 的取值,我们将得到
的取值,我们将得到

如果 满足
满足
 (16)
(16)
则有

其中
 (17)
(17)
通过积分可得

则 在有限时间
在有限时间
 (18)
(18)
熄灭,且(8)成立。
接下来我们来证明第二种情况,即 或者
或者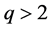 。设
。设 是下面问题
是下面问题

的唯一正解,那么易验证当 时,如果
时,如果 ,则
,则 是(1)的一个上解。
是(1)的一个上解。
当 或者
或者 时。由(1)可得
时。由(1)可得
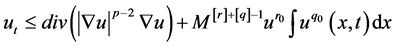 (19)
(19)
其中[]表示取整函数。 ,
, 由此可得
由此可得 ,以下可用与第一种情况完全相同的方法证明,由此本定理证明结束。
,以下可用与第一种情况完全相同的方法证明,由此本定理证明结束。
致谢
作者衷心感谢导师陈玉娟教授的悉心指导和热心鼓励,感谢江苏省大学生实践创新计划项目2012JSSPITP1493的支持,感谢审稿专家对稿件进行了认真的审阅并提出了宝贵的意见。
项目基金
江苏省大学生实践创新计划项目(2012JSSPITP1493),南通大学杏林学院大学生创新训练计划项目。
文章引用
张海星,郝瑞亚,沈娟娟,甘双龙,陈 浪, (2014) 带非局部源的p-Laplace发展方程解的熄灭
Extinction for a Class of p-Laplace
Evolution Equation with
Nonlocal Sources. 应用数学进展,02,119-126. doi: 10.12677/AAM.2014.32018
参考文献 (References)
- 1. Kalashnikov, A.S. (1974) The propagation of disturbances in problems of nonlinear heat conduction with absorption. USSR Computational Mathematics and Mathematical Physics, 14, 70-85.
- 2. Lair, A.V. (1993) Finite extinction time for solutions of nonlinear parabolic equations. Nonlinear Analysis: Theory, Methods & Applications, 21, 1-8.
- 3. Lair, A.V. and Oxley, M.E. (1994) Extinction in finite time for a nonlinear absorption diffusion equation. Journal of Mathematical Analysis and Applications, 182, 857-866.
- 4. Lair, A.V. and Oxley, M.E. (1994) Finite extinction time for a nonlinear parabolic Neumann boundary value problem. Applied Analysis, 55, 41-50.
- 5. 顾永耕 (1994) 抛物型方程的解熄灭的充要条件. 数学学报, 37, 73-79.
- 6. Li, Y.X. and Wu, J.C. (2005) Extinction for fast diffusion equations with nonlinear sources. Electronic Journal of Dif- ferential Equations, 2005, 1-7.
- 7. Wang, M.X. and Wang, Y.M. (1996) Properties of positive solutions for non-local reaction-diffusion problems. Ma- thematical Methods in the Applied Sciences, 19, 1141-1156.
- 8. Lin, Z.G. and Liu, Y.R. (2004) Uniform blow up profiles for diffusion equations with nonlocal source and nonlocal boundary. Acta Mathematica Scientia, 24, 443-450.
- 9. 陈玉娟 (2006) 非局部的退化抛物型方程组的解的爆破和整体存在性. 数学物理学报, 26A, 731-740.
- 10. Fang, Z.B. and Xu, X.H. (2012) Extinction behavior of solutions for the p-Laplacian equations with nonlocal sources. Nonlinear Analysis: Real World Applications, 13, 1780-1789.
- 11. Han, Y.Z. and Gao, W.J. (2011) Extinction for a fast diffusion equation with a nonlinear nonlocal source. Archiv der Mathematik, 97, 353-363.
- 12. Tian, Y. and Mu, C.L. (2008) Extinction and non-extinction for a p-Laplacian equation with nonlinear source. Nonlinear Analysis, 69, 2422-2431.