Advances in Applied Mathematics
Vol.05 No.04(2016), Article ID:19032,6
pages
10.12677/AAM.2016.54076
Research on Posedness of Ternary Graded Interpolation
Ying Liu, Xiaoqian Fan, Lihong Cui
Liaoning Normal University, Dalian Liaoning

Received: Nov. 3rd, 2016; accepted: Nov. 19th, 2016; published: Nov. 24th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Multifunction interpolation is a classic but complex issue. Based on the previous binary graded interpolation research, we study the ternary graded interpolation further. Firstly, we give the definition of ternary graded space, then we explore the well-posedness of the ternary interpolation node group in the European space. We generalize the recursive structure principle to ternary space, and then construct new properly posed node group by adding bevel plane. Lastly, we research the problem of structuring the nodes group of ternary graded interpolation by adding plane and quadric surface, and show the calculation results of the practical examples by using MATLAB.
Keywords:Ternary Graded Interpolation, Properly Posed Node Group, Ternary Polynomial

关于三元分次插值适定性的研究
刘莹,范晓倩,崔利宏
辽宁师范大学,辽宁 大连

收稿日期:2016年11月3日;录用日期:2016年11月19日;发布日期:2016年11月24日

摘 要
多元函数插值是一个经典而又复杂的问题,本文在以往二元分次插值研究的基础上,进一步对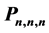 的三元分次插值问题进行探究。首先给出了三元分次空间的定义,进而在欧式空间中对三元插值结点组的适定性进行了探索。将递归构造原理具体到三元空间,通过添加斜平面法来证明构造新的插值适定结点组。然后,通过添加平面和二次代数曲面研究了构造三元分次多项式插值的适定结点问题,并使用MATLAB软件对实际应用的例题计算结果进行了展示。
的三元分次插值问题进行探究。首先给出了三元分次空间的定义,进而在欧式空间中对三元插值结点组的适定性进行了探索。将递归构造原理具体到三元空间,通过添加斜平面法来证明构造新的插值适定结点组。然后,通过添加平面和二次代数曲面研究了构造三元分次多项式插值的适定结点问题,并使用MATLAB软件对实际应用的例题计算结果进行了展示。
关键词 :三元分次插值,适定结点组,三元多项式

1. 引言
多元函数插值一直是计算数学中的一个重要的研究课题。近些年来,人们在解决某些科学计算问题时,常常要涉及多元函数插值问题,在许多实际问题中,常常涉及到 代数(多元函数的计算,散乱数据插值及拟合,曲面外形设计和有限元格式建立等)。这使得有关多元函数插值理论与方法的研究越来越受到相关领域专家和学者的关注。对多元分次插值问题研究最早的是梁学章教授 [1] [2] ,在1965年,他给出了二元分次多项式插值适定结点组的构造方法,构造出了竖线型(横线型),十字型等各种适定结点组,后来又给出了迭加插值法,朱平与傅凯新 [3] 在此基础上在文献中向高维情况做了推广,姜志敏 [4] 也将构造沿平面代数曲线的插值适定结点组的方法进一步推广,有了新的发现。利用无重复分量代数曲面上的分次插值适定结点组的构造方法,我们又得到了构造三维空间中分次插值适定结点组的递归构造方法。
代数(多元函数的计算,散乱数据插值及拟合,曲面外形设计和有限元格式建立等)。这使得有关多元函数插值理论与方法的研究越来越受到相关领域专家和学者的关注。对多元分次插值问题研究最早的是梁学章教授 [1] [2] ,在1965年,他给出了二元分次多项式插值适定结点组的构造方法,构造出了竖线型(横线型),十字型等各种适定结点组,后来又给出了迭加插值法,朱平与傅凯新 [3] 在此基础上在文献中向高维情况做了推广,姜志敏 [4] 也将构造沿平面代数曲线的插值适定结点组的方法进一步推广,有了新的发现。利用无重复分量代数曲面上的分次插值适定结点组的构造方法,我们又得到了构造三维空间中分次插值适定结点组的递归构造方法。
2. 基本概念及引理
设 是非负整数,且
是非负整数,且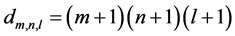 ,而
,而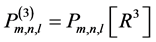 来表示所有关于
来表示所有关于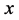 次数不超过
次数不超过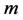 ,关于
,关于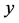 的次数不超过
的次数不超过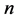 ,关于
,关于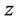 的次数不超过
的次数不超过 三元实系数多项式空间。即
三元实系数多项式空间。即
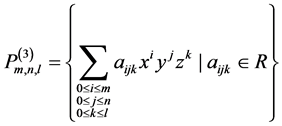
定义1 [5] 设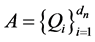 是
是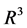 中的
中的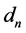 个相异点,对于一个任意给定的实数组
个相异点,对于一个任意给定的实数组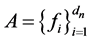 ,寻找一个多项式
,寻找一个多项式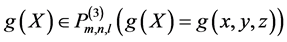 使之满足如下插值条件:
使之满足如下插值条件:
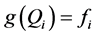 ,
,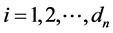 (1)
(1)
如果对于每一个任意给定的实数组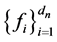 ,方程组(1)总存在唯一的一组解,则称该插值问题是关于多项式空间
,方程组(1)总存在唯一的一组解,则称该插值问题是关于多项式空间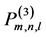 适定插值问题(或称该插值问题是适定的),并称相应的插值结点组
适定插值问题(或称该插值问题是适定的),并称相应的插值结点组 为
为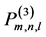 的一个插值适定结点组。
的一个插值适定结点组。
本文中,我们规定,与坐标轴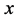 轴垂直的平面称为竖平面,与
轴垂直的平面称为竖平面,与 轴垂直的平面称为纵平面,与
轴垂直的平面称为纵平面,与 轴垂直的平面称为横平面。
轴垂直的平面称为横平面。
引理1 [6] 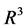 中的
中的 个相异点
个相异点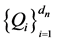 能够做成
能够做成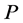 中的适定结点组的充要条件是:
中的适定结点组的充要条件是: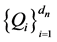 不落在
不落在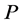 中任何一条代数曲面上。(我们称
中任何一条代数曲面上。(我们称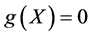 为
为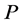 中的代数曲面,如果
中的代数曲面,如果 且
且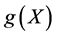 不恒等于0 [1] 。
不恒等于0 [1] 。
引理2 [7] 设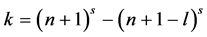 ,其中
,其中 ,
,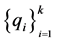 是
是 次无重复分量代数超曲面
次无重复分量代数超曲面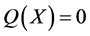 上的
上的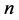 次分次插值适定结点组的充要条件:
次分次插值适定结点组的充要条件:
对所有满足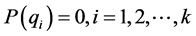 的
的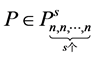 ,均有
,均有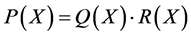 成立,其中
成立,其中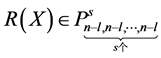 ,当
,当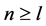 时。
时。
证明:只需证明必要性。
设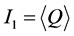 ,
,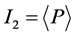 ,若
,若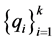 是代数超曲面
是代数超曲面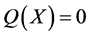 上的
上的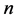 次分次差值适定结点组,且
次分次差值适定结点组,且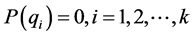 ,那么,在超曲面
,那么,在超曲面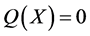 上有
上有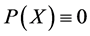 ,即
,即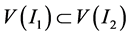 ,由命题有
,由命题有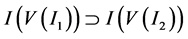 。注意到
。注意到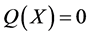 无重复分量的代数多项式,所以有
无重复分量的代数多项式,所以有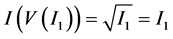 ,另一方面
,另一方面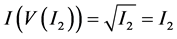 ,从而
,从而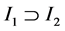 ,由理想的定义有
,由理想的定义有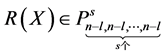 使得
使得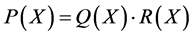 。证毕。
。证毕。
引理3 [5] (递归构造定理)设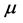 是
是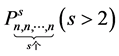 的适定结点组,
的适定结点组,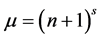 ,做一个
,做一个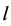 次无重复分量的代数超曲面
次无重复分量的代数超曲面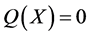 ,使其不通过
,使其不通过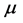 中任何点,任取超曲面
中任何点,任取超曲面 上的
上的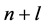 次分次插值适定结点组
次分次插值适定结点组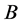 ,则
,则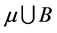 必是
必是 的插值适定结点组。
的插值适定结点组。
证明: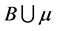 所含点数为
所含点数为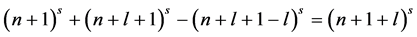 ,恰为
,恰为 的维数,下面证明其适定性,用反证法。
的维数,下面证明其适定性,用反证法。
假设点组 不是
不是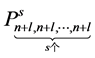 的插值适定结点组,则必有不恒为零的
的插值适定结点组,则必有不恒为零的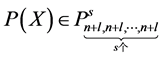 ,使得
,使得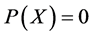 通过
通过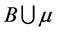 中的点。特别的,
中的点。特别的, 通过
通过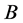 中的点,注意到
中的点,注意到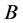 是代数超曲面
是代数超曲面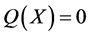 上的
上的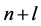 次分次插值适定结点组,故有
次分次插值适定结点组,故有 使得
使得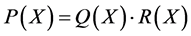 ,又
,又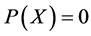 通过超曲面
通过超曲面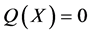 以外的点组
以外的点组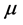 ,则
,则 通过
通过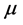 中的点,而这与
中的点,而这与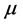 是
是 的适定结点组矛盾。证毕。
的适定结点组矛盾。证毕。
3. 主要结果及证明
由引理2具体到三元分次空间,我们可以得到:
定理1 设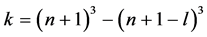 ,
, 是
是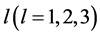 次无重复分量的曲面
次无重复分量的曲面 上的
上的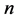 次分次插值适定结点组的充要条件是:
次分次插值适定结点组的充要条件是:
对所有满足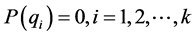 的
的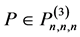 均有如下分解:
均有如下分解:
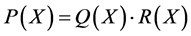
其中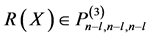 ,当
,当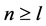 时。
时。
定理2:设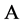 是
是 的适定结点组,
的适定结点组,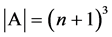 ,不通过
,不通过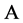 中任何点作一个平面
中任何点作一个平面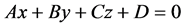 (
( 均不为零),任取该平面上的
均不为零),任取该平面上的 次分次插值适定结点组
次分次插值适定结点组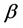 ,则
,则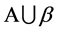 必是
必是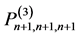 的插值适定结点组。
的插值适定结点组。
证明:分次插值空间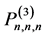 的维数是
的维数是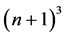 ,
,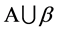 所含的点数为
所含的点数为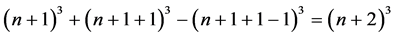 ,这恰好是
,这恰好是 的维数。下用反证法证明其适定性。
的维数。下用反证法证明其适定性。
假设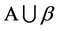 不是
不是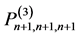 的适定结点组,则必有不恒为零的
的适定结点组,则必有不恒为零的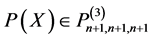 使得
使得 通过
通过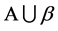 中的点,特别地,
中的点,特别地,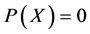 会通过
会通过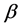 中的点,注意到
中的点,注意到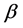 是
是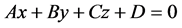 平面上的
平面上的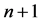 次分次插值适定结点组,故有
次分次插值适定结点组,故有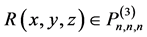 ,使得
,使得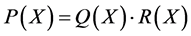 ,又
,又 通过
通过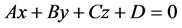 平面以外的点组
平面以外的点组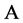 ,则
,则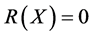 通过
通过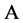 中的点,而这与
中的点,而这与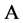 是
是 的适定结点组矛盾。证毕。
的适定结点组矛盾。证毕。
4. 具体构造方法及实验示例
三元欧式空间中,分次插值适定结点组的构造方法如下:
在空间中,任取一点都可以作成空间中的0次分次插值适定结点组,下面给出在三维空间中构造分次插值适定结点组的两种方法。
1) 添加平面法
第0步,在空间中任取一点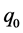 ,它一定是
,它一定是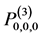 的适定结点组;
的适定结点组;
第1步,不过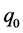 点作一个平面,在平面上任取7个互不相同的点
点作一个平面,在平面上任取7个互不相同的点 与
与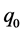 一起构成
一起构成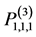 的适定结点组;
的适定结点组;
……
第 步,不过上面所有点,做一个平面,在这个平面上任取
步,不过上面所有点,做一个平面,在这个平面上任取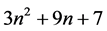 个互不相同的点。
个互不相同的点。
到第 步结束后,得到的所有的点的组合便构成
步结束后,得到的所有的点的组合便构成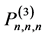 的分次适定结点组。
的分次适定结点组。
2) 添加二次代数曲面法
第0步,在空间中任取一点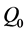 ,它一定是
,它一定是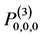 的适定结点组;
的适定结点组;
第1步,不过 点,作一个二次代数曲面,在其上任取26个互不相同的点,与
点,作一个二次代数曲面,在其上任取26个互不相同的点,与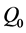 一起构成
一起构成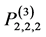 的适定结点组;
的适定结点组;
……
第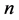 步,不过上面所有点,做一个二次代数平面,在曲面上任取
步,不过上面所有点,做一个二次代数平面,在曲面上任取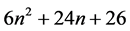 个互不相同的点。
个互不相同的点。
到第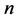 步结束后,得到的所有的点的组合便构成
步结束后,得到的所有的点的组合便构成 的适定结点组。
的适定结点组。
例题:设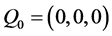 为
为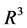 上任意一点,
上任意一点,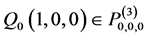 ,在平面
,在平面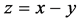 上任取7个点,
上任取7个点,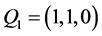 ,
,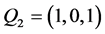 ,
,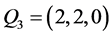 ,
,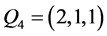 ,
,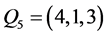 ,
,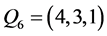 ,
,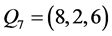 ,且
,且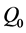 不在平面
不在平面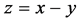 上,则
上,则 这八个点构成空间
这八个点构成空间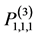 的插值适定结点组。
的插值适定结点组。
设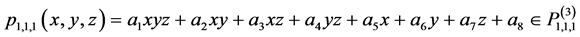 ,将相应的点代入
,将相应的点代入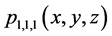 并令其为零,便得到一个8阶的齐次线性方程组,系数行列式如下:
并令其为零,便得到一个8阶的齐次线性方程组,系数行列式如下:
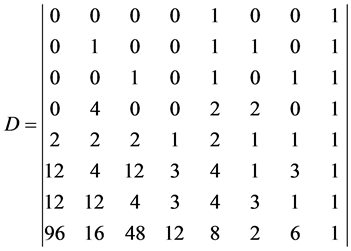
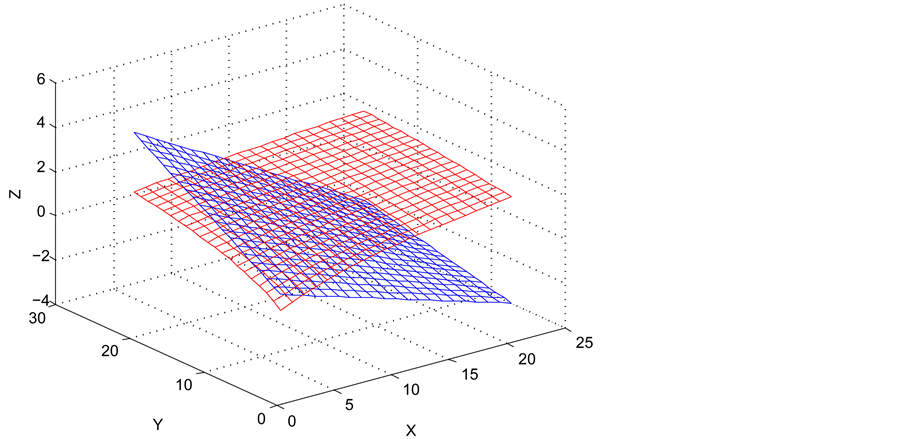
Figure 1. The effect diagram of ternary graded interpolation
图1. 三元分次插值效果图
由于 ,因此
,因此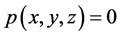 解唯一存在。
解唯一存在。
设一个被插曲面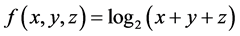 ,将这八个点代入
,将这八个点代入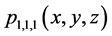 和
和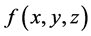
解得: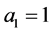 ,
,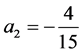 ,
,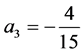 ,
,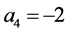 ,
,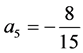 ,
,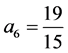 ,
,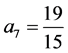 ,
,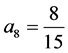 ,
,
所以确定唯一的插值曲面:
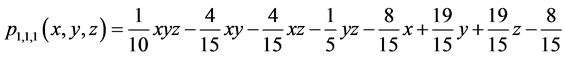 。
。
由MATLAB做出被插值函数与所求多项式的图像如图1所示。
致谢
在本篇论文完成的同时,我首先要感谢我的导师崔利宏老师。在崔老师的悉心指导下,我的论文才能如此顺利的完成。在本篇论文的完成过程中,崔老师对我提出了很多建设性的指导意见,细心地和我讲解论文中出现的问题,给予专业上的指导,信心上的鼓励。同时我也要感谢学校和学校的领导给我们创造的良好的学习环境,让我们能够在良好的氛围中完成论文。感谢同学和家人在这期间的大力支持。
基金项目
辽宁大学生实践基地建设项目基金资助。
文章引用
刘莹,范晓倩,崔利宏. 关于三元分次插值适定性的研究
Research on Posedness of Ternary Graded Interpolation[J]. 应用数学进展, 2016, 05(04): 651-656. http://dx.doi.org/10.12677/AAM.2016.54076
参考文献 (References)
- 1. 梁学章, 李强. 多元逼近[M]. 北京: 国防工业出版社, 2005.
- 2. 崔利宏, 梁学章. 关于中Lagrange插值适定结点组结构问题的研究[J]. 辽宁师范大学学报, 2004, 27(4): 392-398.
- 3. 朱平, 傅凯新. 十字型结点组及R2上的插值[J]. 高等学校计算数学学报, 1995(1): 12-20.
- 4. 崔利宏, 姜志敏. 关于多元分次插值结点组适定性问题的研究[J]. 延边大学学报(自然科学版), 2008, 34(2): 86-88.
- 5. 崔利宏. 多元Lagrange插值与多元Kergin插值[D]: [博士学位论文]. 长春: 吉林大学, 2003.
- 6. Liang, X.Z., Cui, L.H. and Zhang, J.L. (2002) Properly Posed Set of Nodes for Bivariate Lagrange Interpolation along an Algebraic Curve. Analysis,Combinatories and Computing, Nova Science Publishers Inc., American, 10.
- 7. 徐艳, 野金花. 多元空间分次插值适定结点组的几何结构[J]. 黑龙江八一农垦大学学报, 2009, 21(6): 80-82.