Advances in Applied Mathematics
Vol.06 No.01(2017), Article ID:19641,14
pages
10.12677/AAM.2017.61011
Convergence Analysis of the Two-Step Combined Method for Solving Nonlinear Operator Equations
Weidi Wu, Weiping Shen, Lihua Xu
Department of Mathematics, Zhejiang Normal University, Jinhua Zhejiang

Received: Jan. 3rd, 2017; accepted: Jan. 21st, 2017; published: Jan. 24th, 2017
Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, we consider the convergence of the two-step combined method for solving nonlinear operator equations. A semi-local convergence of the method is presented under some continuity conditions. Moreover, we establish the uniqueness result of the solutions. Finally, a numerical example is provided to demonstrate our theoretical results.
Keywords:Semi-Local Convergence, Two-Step Combined Method, Divided Differences

求解非线性算子方程的两步组合方法的收敛性分析
吴伟笛,沈卫平,徐丽华
浙江师范大学数学系,浙江 金华

收稿日期:2017年1月3日;录用日期:2017年1月21日;发布日期:2017年1月24日

摘 要
本文考虑求解非线性方程问题的两步组合方法的收敛性。在某些连续性条件下,我们给出了该方法的半局部收敛性。另外对算子方程的解的唯一性也做出了说明。最后通过数值例子来说明收敛性分析的有效性。
关键词 :半局部收敛性,两步组合方法,差商

1. 引言
设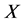 与
与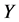 为Banach空间,且
为Banach空间,且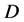 为
为 中的一开凸子集。考虑非线性算子方程
中的一开凸子集。考虑非线性算子方程
 (1)
(1)
其中, 为定义在
为定义在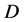 上的一个非线性算子。
上的一个非线性算子。
众所周知,牛顿法是求解方程(1)的最著名的方法之一。其中,文献 [1] 及 [2] 研究了在算子 的一阶导数满足
的一阶导数满足 条件下牛顿法的平方收敛性结果。
条件下牛顿法的平方收敛性结果。
在文章 [3] 中,M. Bartish首次提出了两步修正牛顿法:
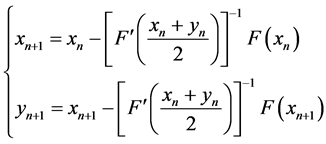 对任意的
对任意的 (2)
(2)
并且在康托洛维奇型条件下给出了该算法的半局部收敛性。这里, ,
, 为给定的初始值。此外,文章 [4] [5] [6] [7] [8] 对该算法及其收敛性也做了一定的研究。
为给定的初始值。此外,文章 [4] [5] [6] [7] [8] 对该算法及其收敛性也做了一定的研究。
同样,通过引入了差商的定义,M. Bartish在文章 [3] 中给出了不同于(2)的如下两步算法来求解方程(1):
 对任意的
对任意的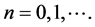 (3)
(3)
这里,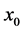 ,
, 为给定的初始值,
为给定的初始值,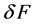 为由
为由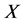 到
到 的有界线性算子。很多学者对算法(3)的收敛性也作出了一定的研究。例如,文 [9] 在相对弱的康托洛维奇条件下对算法(3)的半局部收敛性进行了研究。再如,类似 [10] [11] [12] 中古典割线法的收敛条件,S. M. Shakhno研究了仅在
的有界线性算子。很多学者对算法(3)的收敛性也作出了一定的研究。例如,文 [9] 在相对弱的康托洛维奇条件下对算法(3)的半局部收敛性进行了研究。再如,类似 [10] [11] [12] 中古典割线法的收敛条件,S. M. Shakhno研究了仅在 条件下算法(3)的收敛性问题。又如,文章 [13] 与 [14] 给出了二阶均差满足
条件下算法(3)的收敛性问题。又如,文章 [13] 与 [14] 给出了二阶均差满足 条件下该方法的收敛性定理。另外,文章 [15] 及 [16] 也对算法(3)的收敛性进行了研究。特别地,当算子
条件下该方法的收敛性定理。另外,文章 [15] 及 [16] 也对算法(3)的收敛性进行了研究。特别地,当算子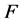 满足下列条件时:
满足下列条件时:
 (4)
(4)
文章 [16] 给出了算法(3)的半局部收敛性以及方程(1)的解的唯一性。这里, ,
, 。
。
下面,我们考虑非线性算子方程
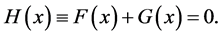 (5)
(5)
这里, 均为定义在
均为定义在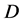 上的非线性算子。
上的非线性算子。 为Fréchet可微算子,
为Fréchet可微算子, 为连续算子。最近,S. M. Shakhno等通过结合算法(2)与(3)在文章 [17] 中首次提出了下列两步组合方法用于求解方程(5):
为连续算子。最近,S. M. Shakhno等通过结合算法(2)与(3)在文章 [17] 中首次提出了下列两步组合方法用于求解方程(5):
 对任意的
对任意的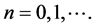 (6)
(6)
其中, 为给定的初始值。文章 [18] 通过假设
为给定的初始值。文章 [18] 通过假设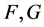 满足带有积分形式的
满足带有积分形式的 条件,给出该算法的局部收敛性结果,并且证明了它的收敛阶为
条件,给出该算法的局部收敛性结果,并且证明了它的收敛阶为 。
。
在这篇文章中,我们讨论用于求解方程(5)的两步组合方法的半局部收敛性问题。当算子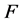 的一阶F-导数满足
的一阶F-导数满足 条件,二阶导数满足
条件,二阶导数满足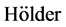 条件以及算子
条件以及算子 的差商满足
的差商满足 条件下,我们给出了该方法的收敛性定理, 并证明了解的唯一性。另外,在最后一节中,我们还给出了一个数值例子来说明我们理论结果。
条件下,我们给出了该方法的收敛性定理, 并证明了解的唯一性。另外,在最后一节中,我们还给出了一个数值例子来说明我们理论结果。
2. 定义与引理
本节中,我们给出一些基本的定义及引理。
定义1 [16] 假设 表示由
表示由 到
到 的一个线性算子。设
的一个线性算子。设 ,若
,若 满足条件:
满足条件:
 (7)
(7)
则称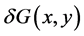 为在点
为在点 的差商。
的差商。
引理2 (Banach引理 [19] ) 设 的有界线性算子,
的有界线性算子, 且为单位算子,若
且为单位算子,若 则
则 为可逆的且有
为可逆的且有
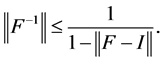
引理3 [8] 已知 ,
, 。设
。设 表示所有连续可微的且二阶导数
表示所有连续可微的且二阶导数 连续的全体算子。
连续的全体算子。
假设(1)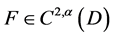 。
。
(2) 可逆且存在非负数
可逆且存在非负数 使得
使得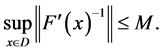
(3) ,
,
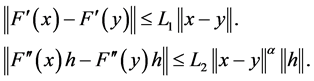
则有
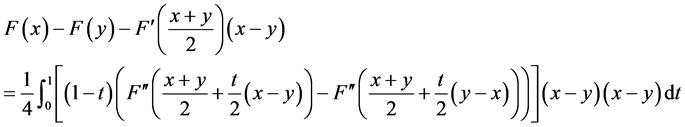
3. 半局部收敛性定理
下面,我们建立两步组合方法的半局部收敛性定理。在下面的讨论中,我们令 表示以
表示以 为中心以
为中心以 为半径的闭球。假设算子
为半径的闭球。假设算子 的一阶F-导数
的一阶F-导数 和二阶
和二阶 -导数
-导数 ,以及算子
,以及算子 的差商
的差商 均存在。设
均存在。设 为
为 中的两点。令
中的两点。令 其中
其中
定理1假设(1)算子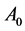 可逆;
可逆;
(2)存在非负常数 及
及 ,使得对
,使得对 ,下列条件成立:
,下列条件成立:
 (8)
(8)
 (9)
(9)
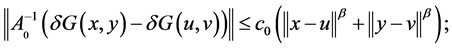 (10)
(10)
(3) 且存在非负数
且存在非负数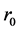 使得
使得
 (11)
(11)
其中

(4) 闭球 。假设实序列
。假设实序列 由如下定义:
由如下定义:
 (12)
(12)
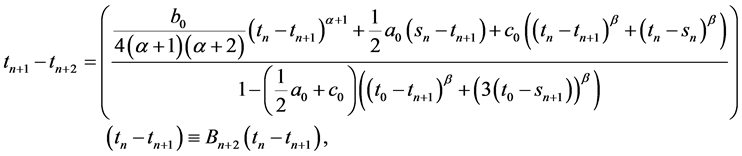 (13)
(13)
 (14)
(14)
则我们有如下结论:
(i) 为非负,递减序列且收敛于
为非负,递减序列且收敛于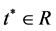 满足
满足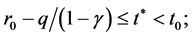
(ii)算法(6)是适定的。所得序列 收敛于解
收敛于解 ,且满足不等式
,且满足不等式
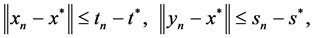 对任意
对任意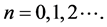 (15)
(15)
并且解是唯一的。特别的,当 时,我们有
时,我们有
 (16)
(16)
证明:(i) 我们用数学归纳法证明下列不等式是成立的:
 (17)
(17)
以及
 (18)
(18)
其中,由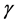 定义,有
定义,有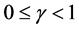 。那么由序列递减且有下界,就可得序列
。那么由序列递减且有下界,就可得序列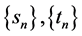 是收敛的。因此,由
是收敛的。因此,由
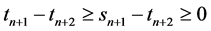 及
及
即可得 从而
从而 也收敛。
也收敛。
首先,当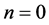 时,由式子(12),(13),(14),我们可以得到
时,由式子(12),(13),(14),我们可以得到
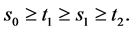
又由于

因此
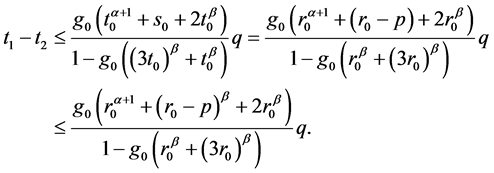
即可得

所以

并且

即当 时,(17)与(18)成立。假设
时,(17)与(18)成立。假设 时,不等式(17)与(18)是成立的,即
时,不等式(17)与(18)是成立的,即

且

则当 时,
时,
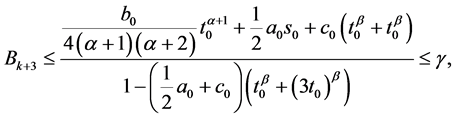 (19)
(19)
 (20)
(20)
由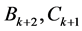 定义及假设,可得
定义及假设,可得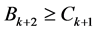 。由条件(13),(14)及假设,我们可得:
。由条件(13),(14)及假设,我们可得:

以及

又由条件(13)及(19),

所以

因此,由上式及 定义可得
定义可得

综上可得

即可得(17)与(18)对 是成立的。从而,我们证得(i)成立。
是成立的。从而,我们证得(i)成立。
下面给出(ii)的证明。我们将用数学归纳法证明迭代过程(6)是适定的且有
 (21)
(21)
因此

当 时,显然,由算法(6),
时,显然,由算法(6), 定义及(12),很容易可以证明(21)是成立的。现假设
定义及(12),很容易可以证明(21)是成立的。现假设 为非负整数,并且对所有
为非负整数,并且对所有 ,不等式(21)是成立的。若令
,不等式(21)是成立的。若令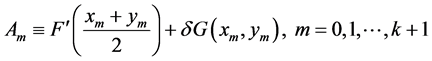 ,则有
,则有
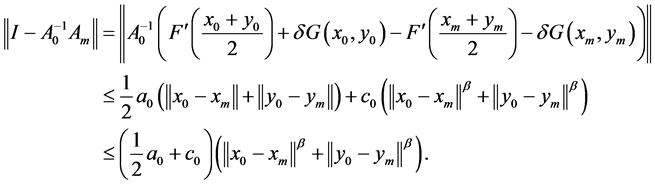 (22)
(22)
由假设及条件(11)
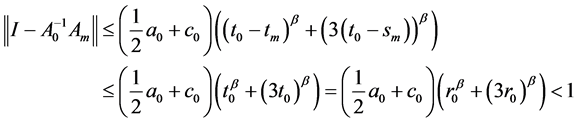 (23)
(23)
则由引理2, 为可逆的,并且
为可逆的,并且
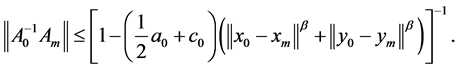 (24)
(24)
下证当 时,迭代过程是可以定义的。
时,迭代过程是可以定义的。
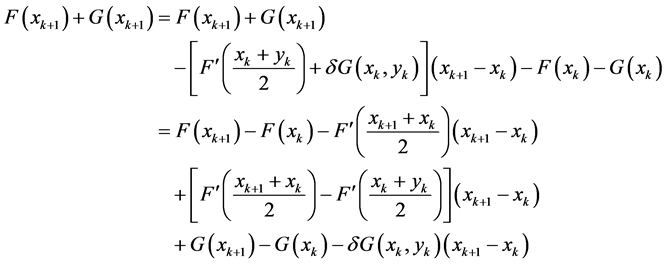 (25)
(25)
由引理3,有

因此,我们可以得到
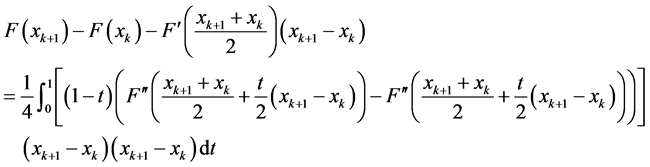
另外由均差定义,有

所以
 (26)
(26)
所以,由上可得


然后,由(21),(13),(14),我们可得
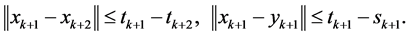 (27)
(27)
因此,即可证得迭代方法对任意 是可以定义的。又由
是可以定义的。又由
 (28)
(28)

以及前面已证的 及
及 也收敛,就证得了
也收敛,就证得了 ,
, 为柯西序列且是收敛的。不妨设
为柯西序列且是收敛的。不妨设 ,因此,在(28)中,当
,因此,在(28)中,当 时,我们便可以得到(15)是成立的,即
时,我们便可以得到(15)是成立的,即
 (29)
(29)
又因为当 时,有
时,有

所以我们即可得 即为方程
即为方程 的根。
的根。
接下来我们证明(16)是成立的。由等式
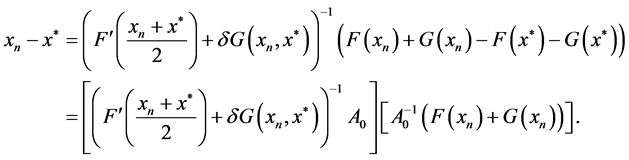
由条件(28),(29),(8),(9),(10)知
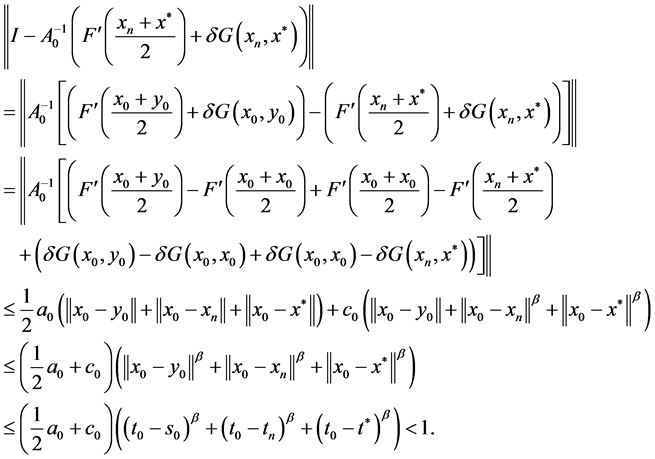
所以由引理2,线性算子 为可逆的,且有
为可逆的,且有

另外,(26)可得
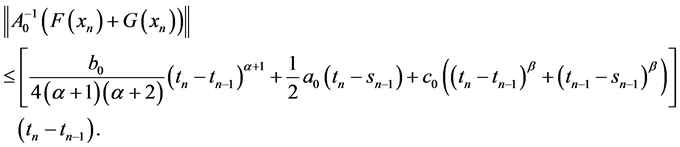
所以

下面我们证解的唯一性。由(11)式,我们可以得到
 (30)
(30)
设 为方程
为方程 在
在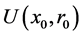 上的另一解,其中
上的另一解,其中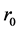 是满足(12)式。则由迭代算法(5),(8),(9)及(1)我们可以得
是满足(12)式。则由迭代算法(5),(8),(9)及(1)我们可以得

因此,由式子(24),(8),(10)及引理3,我们即可得

下面我们用数学归纳法证明 是小于1的。首先,由式(14),我们可得
是小于1的。首先,由式(14),我们可得
 (31)
(31)
当 时由式(30),(31)及
时由式(30),(31)及

所以有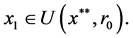 假设当
假设当 时,有
时,有 则当
则当 时,由假设及式(30),(31),我们有
时,由假设及式(30),(31),我们有

取 表示
表示 的上界,则有
的上界,则有 。
。

当 时,
时, 所以
所以
所以唯一性得证。
4. 数值例子
本文将引用文献 [16] 中的例子验证定理1中的条件是非空的。考虑下面的二阶非线性边界值问题:
 (32)
(32)
将[0,1]分成 个子区间,
个子区间, 表示细分的点,且有
表示细分的点,且有 。令
。令 我们给出一个二阶导数的标准近似:
我们给出一个二阶导数的标准近似:
取 ,则将
,则将 代入问题(32),我们即可得
代入问题(32),我们即可得
 (33)
(33)
因此我们可得方程组(33)的系数矩阵
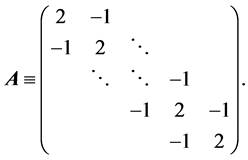
另外,对于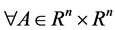 ,相应的有范数
,相应的有范数 。定义
。定义

令 其中
其中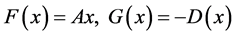 ,显然
,显然
接下来我们对 做一些相关计算。由文献 [10] , [11] , [12] ,
做一些相关计算。由文献 [10] , [11] , [12] , 可以由矩阵的元素来表示:
可以由矩阵的元素来表示:

这里
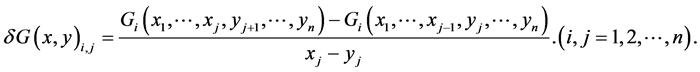
由均差定义,我们可以把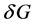 转化为积分的形式(参见文献 [16] ):
转化为积分的形式(参见文献 [16] ):

注意到,对所有 。
。

由此
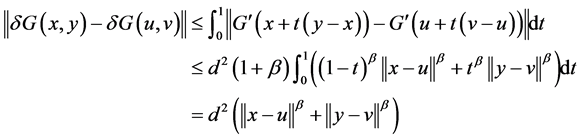 (34)
(34)
所以

最后,易知

即对条件(8),(9),(10)中的系数 均取为
均取为 。
。
我们选定下组数据作为初始值:

下面我们通过计算来验证定理1的结论。为此,取 ,通过定理1及上面说明,我们可得:
,通过定理1及上面说明,我们可得:
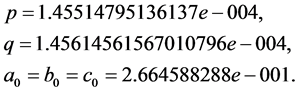
取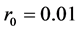 ,则通过计算(13),(14),(15)可得:
,则通过计算(13),(14),(15)可得:

由上面计算,我们可以看出定理1中的条件是非空的,即存在这样的一组数据满足定理1的条件。
基金项目
浙江省自然科学基金资助项目(LY17A010006)。
文章引用
吴伟笛,沈卫平,徐丽华. 求解非线性算子方程的两步组合方法的收敛性分析
Convergence Analysis of the Two-Step Combined Method for Solving Nonlinear Operator Equations[J]. 应用数学进展, 2017, 06(01): 90-103. http://dx.doi.org/10.12677/AAM.2017.61011
参考文献 (References)
- 1. Kantorovich, L.V. and Akilov, G.P. (1982) Functional Analysis. Pergamon, Oxford.
- 2. Ortega, J.M., Rheinboldt, W.C. (1970) Iterative Solution of Nonlinear Equations in Several Variable. Academic Press, New York.
- 3. Ya, B.M. (1968) About One Iterative Method of Solving Functional Equations. Dopovidi Akademii Nauk Ukrains'koi RSR seriya A, 5, 387-391.
- 4. Argyros, I.K. (2011) On the Semi-Local Convergence of Werner’s Method for Solving Equations Using Recurrent Functions. Punjab University journal of mathematics, 43, 19-28.
- 5. Han, D. and Wang, X. (1998) Convergence of Deformed Newton Method. Applied Mathematics and Computation, 94, 65-72. https://doi.org/10.1016/S0096-3003(97)10066-2
- 6. King, R.F. (1972) Tangent Method for Nonlinear Equations. Numerische Mathematik, 18, 298-304. https://doi.org/10.1007/BF01404680
- 7. Laasonen, P. (1969) Einüberquadratisch konvergenter iterativer algorithmus. Annales Academia Scientiarum Fennica.series A, 450, 1-10.
- 8. Werner, W. (1979) On an Order Method for Solving Nonlinear Equations. Numerische Mathematik, 32, 333-342. https://doi.org/10.1007/BF01397005
- 9. Kantorovich, L.V. and Akilov, G.P. (1984) Functional Analysis, Nauka, Moscow (in Russian).
- 10. Argyros, I.K. (1991) On an Iterative Algorithm for Solving Nonlinear Operator Equations. Journal of Analysis and Its Applications, 10, 83-92. https://doi.org/10.4171/ZAA/433
- 11. Hernandez, M. and Rubio, M.J. (2001) The Secant Method and Divided Differences Hölder Continuous, Applied Mathematics and Computation, 124, 139-149. https://doi.org/10.1016/S0096-3003(00)00079-5
- 12. Shakhno, S.M. (2004) Application of Nonlinear Majoriants for Investigation of the Secant Method for Solving Nonlinear Equations. Matematychni Studii, 22, 79-86.
- 13. Potra, F.A. (1984-1985) on an Iterative Algorithm of Order 1.839… for Solving Nonlinear Operator Equations. Numerical Functional Analysis and Optimization, 7, 75-106. https://doi.org/10.1080/01630568508816182
- 14. Shakhno, S.M. (2004) On a Kurchatov’s Method of Linear Interpolation for Solving Nonlinear Equations. Proceedings in Applied Mathematics and Mechanics, 4, 650-651. https://doi.org/10.1002/pamm.200410306
- 15. Bartish, M., Shcherbyna, Y. and Yu, M. (1972) About One Difference Method of Solving Operator Equations. Dopovidi Akademii Nauk Ukrains'koi RSR series A, 7, 579-582.
- 16. Shakhno, S.M. (2009) On an Iterative Algorithm with Super-Quadratic Convergence of Solving Nonlinear Operator Equations. Journal of Computational and Applied Mathematics, 231, 222-235. https://doi.org/10.1016/j.cam.2009.02.010
- 17. Shakhno, S.M. and Yarmola, H. (2012) Two-Step Method for Solving Nonlinear Equations with Non-Differentiable Operator. Journal of Computational and Applied Mathematics, 109, 105-115.
- 18. Shakhno, S.M. (2014) Convergence of the Two-Step Combined Method and Uniqueness of the Solution of Nonlinear Operator Equations. Journal of Computational and Applied Mathematics, 261, 378-386. https://doi.org/10.1016/j.cam.2013.11.018
- 19. 李庆杨, 莫孜中, 祁力群. 非线性方程组的数值解法[M]. 北京: 科学出版社, 1999.