Advances in Applied Mathematics
Vol.06 No.03(2017), Article ID:20781,9
pages
10.12677/AAM.2017.63036
Positive Periodic Solutions for a Generalized Prey–Predator Model
Xianglai Zhuo1, Fengxue Zhang2
1College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao Shandong
2College of Mining and Safety Engineering, Shandong University of Science and Technology, Qingdao Shandong

Received: May 7th, 2017; accepted: May 23rd, 2017; published: May 27th, 2017

ABSTRACT
The existence of positive periodic solutions for a generalized prey-predator model with harvesting term was studied by using Mawhin’s continuation theorem of coincidence degree theory. Some sufficient conditions were obtained to ensure the existence of positive periodic solutions. The results obtained in this paper generalized the known results.
Keywords:Coincidence Degree, Prey-Predator Model, Harvesting Term, Positive Periodic Solution
具收获项和周期系数的广义捕食-被捕食模型的正周期解题
卓相来1,张丰雪2
1山东科技大学数学与系统科学学院,山东 青岛
2山东科技大学矿业与安全工程学院,山东 青岛
收稿日期:2017年5月7日;录用日期:2017年5月23日;发布日期:2017年5月27日

摘 要
利用重合度理论,我们研究具收获项的广义捕食-被捕食模型,得到系统存在正周期解的充分条件。本文结果推广了已有文献的结果。
关键词 :重合度理论,捕食-被捕食模型,收获项,正周期解

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
众所周知,具收获项的捕食-被捕食系统可以被描述为 [1] [2] [3] [4]
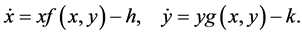
这里 分别表示捕食-被捕食猎物的密度,h和k是收获项 [5] 。特别地,一个具收获项的捕食-被捕食非自治模型可以被描述为
分别表示捕食-被捕食猎物的密度,h和k是收获项 [5] 。特别地,一个具收获项的捕食-被捕食非自治模型可以被描述为
 (1)
(1)
这里 分别表示猎物的内在增长率,捕获率,捕食者的死亡率,转换率和半饱和参数。设(1)的所有参数均正,详细的生态意义可参考 [6] - [11] 及其相应的参考文献。
分别表示猎物的内在增长率,捕获率,捕食者的死亡率,转换率和半饱和参数。设(1)的所有参数均正,详细的生态意义可参考 [6] - [11] 及其相应的参考文献。
由于实际的模型常受到环境变化的影响,因此文 [9] 研究了模型
 (2)
(2)
这里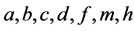 均是连续的正
均是连续的正 周期函数。
周期函数。
本文研究
 (3)
(3)
这里 是连续的正
是连续的正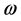 周期函数,n是正整数。显然文 [9] 是本文的特殊情况。
周期函数,n是正整数。显然文 [9] 是本文的特殊情况。
本文用重合度理论研究系统(3)正周期解的存在性。为方便,我们列举(详细请参考 [10] )
引理1 (连续定理)。假设L是指标为零的Fredholm映射,N在 上是L-紧的,若
上是L-紧的,若
(1)对任意 ,对算子方程
,对算子方程 的任一解满足
的任一解满足 。
。
(2)当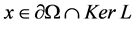 时,
时, ,
, 。
。
则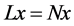 在
在 上至少有一个解。
上至少有一个解。
2. 主要结果
令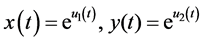 ,则系统(3)成为
,则系统(3)成为
 (4)
(4)
如果 是(4)的
是(4)的 周期解,则
周期解,则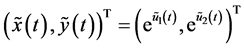 是(3)的
是(3)的 周期解。令
周期解。令
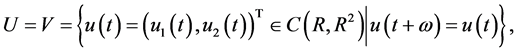
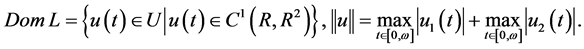
在此范数下,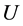 是Banach空间。定义
是Banach空间。定义 和
和 分别为
分别为

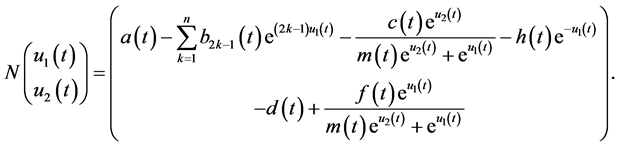
定义投影 和
和 为
为

易知 ,
,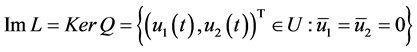 是
是 的闭集,这里
的闭集,这里
 。于是
。于是 是指标为零的Fredholm算子。
是指标为零的Fredholm算子。
为了叙述方便,我们引进下述记号

考虑算子方程 ,这里
,这里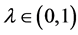 ,即考虑
,即考虑
 (5)
(5)
若对于任意的 ,
, 是(5)的
是(5)的 周期解,令
周期解,令

则
 (6)
(6)
由(5)和(6)得
 (7)
(7)
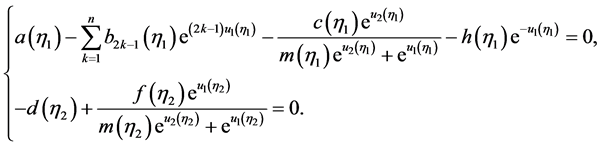 (8)
(8)
为了叙述方便,记

对于函数 ,易证下面的引理(证明略)
,易证下面的引理(证明略)
引理2. 若 是连续的正
是连续的正 周期函数,则对于函数
周期函数,则对于函数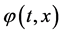 和
和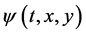 ,我们有
,我们有
(i)对于固定的 ,
, 关于
关于 单调减少。
单调减少。
(ii)对任意的 ,当
,当 时,
时, 。对于固定的
。对于固定的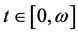 ,当
,当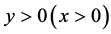 时,
时, 关于
关于 上升,而且当
上升,而且当 时,
时, 关于
关于 上升。
上升。
(iii)对 ,当
,当 时,
时, 。
。
(iv)对 ,当
,当 时,
时, 。
。
(v)对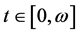 ,当
,当 时,
时, 。
。
定理1. 若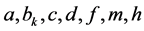 是连续的正
是连续的正 周期函数,则系统(4)至少有一个
周期函数,则系统(4)至少有一个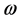 周期解。
周期解。
证明. 由(7)的第一个方程易知 ,由引理2的(iii)知
,由引理2的(iii)知 。由(8)的第一个方程和引理2的(i)知
。由(8)的第一个方程和引理2的(i)知 ,于是对
,于是对 ,
, 。由(7)的第二个方程和引理2(ii)得
。由(7)的第二个方程和引理2(ii)得 ,于是由引理2(iv)得
,于是由引理2(iv)得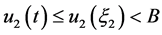 。由(8)的第二个方程和引理2(ii)得
。由(8)的第二个方程和引理2(ii)得 。于是对
。于是对 ,由引理2(v)得
,由引理2(v)得 。故
。故 。
。
记 。
。
 是U的有界开集,我们将证明N在
是U的有界开集,我们将证明N在 是L-紧的。事实上,
是L-紧的。事实上, 满足
满足

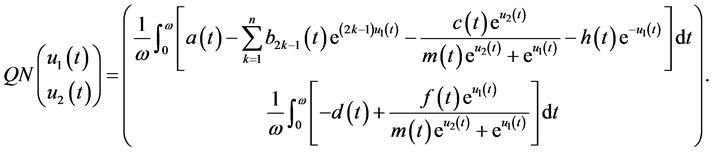
易知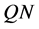 和
和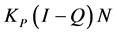 都在
都在 连续,
连续, 在
在 上有界且
上有界且 是紧的,于是
是紧的,于是 是L-紧的。注意到
是L-紧的。注意到 ,所以
,所以 是同构恒等映射。于是引理1的条件(1)成立。
是同构恒等映射。于是引理1的条件(1)成立。
往下我们证明:对于任意的 ,
, 。事实上,若不然,则存在
。事实上,若不然,则存在 使得
使得
 (9)
(9)
由积分中值定理,存在 使
使

用上面同样的证明方法得 。这与
。这与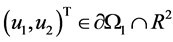 矛盾。
矛盾。
为证明 ,我们预先建立下面的引理。
,我们预先建立下面的引理。
引理3.若 ,
,

则 是同伦映射。
是同伦映射。
证明对于 ,易知
,易知 ,因此只要证明当
,因此只要证明当 或
或 且对于
且对于 ,
, 或
或 时,
时,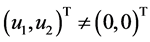 。因
。因 ,所以当
,所以当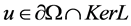 时,
时,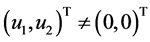 。当
。当 ,
, ,且当
,且当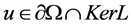 ,
, ,于是只要证明对
,于是只要证明对 ,
, 。
。
若 满足
满足

同样用积分中值定理,存在 使
使
 (10)
(10)
若 ,由引理2(iii),当
,由引理2(iii),当 时,
时, 。于是
。于是
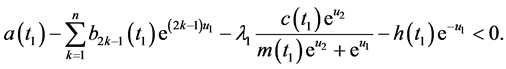
这与(10)的第一个方程矛盾。
若 ,由(10)的第一个方程得
,由(10)的第一个方程得
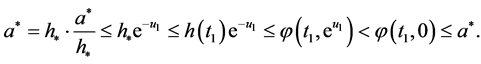
上式不可能成立。
若(10)成立,由(10)的第二个方程及 得
得 。
。
若 ,这与引理2(iv)矛盾;同样当
,这与引理2(iv)矛盾;同样当 时候,
时候,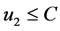 ,(10)的第二个方程不成立。故当
,(10)的第二个方程不成立。故当 时,
时, ,故
,故 在
在 上是同伦映射,因此
上是同伦映射,因此
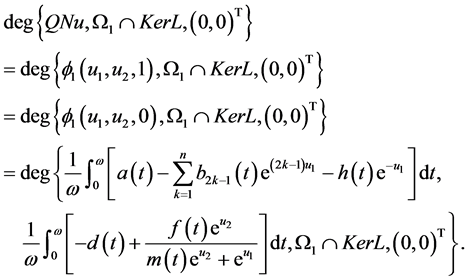
引理4.考虑代数方程组
 (11)
(11)
这里 都是正常数。如果
都是正常数。如果 且
且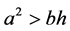 ,则易证(这里从略)
,则易证(这里从略)

由引理4易得(1)当 时,
时, ;(2)当
;(2)当 时,
时, ;
;
(3)当 时,
时,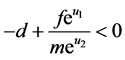 ;
;
(4)当 时,
时, 。
。
记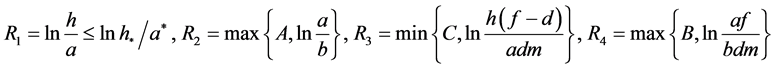 。
。
若 ,则
,则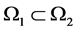 。
。
引理5.若 定义为
定义为

则 在
在 上是同伦映射。
上是同伦映射。
证明我们只需证明下面两个情况
情况1取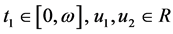 ,使满足
,使满足
 (12)
(12)
则 。事实上,若
。事实上,若 ,由引理2(iii)和引理4得
,由引理2(iii)和引理4得
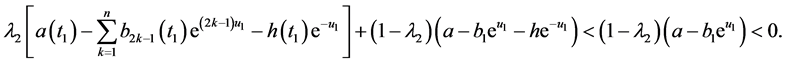 (13)
(13)
若 ,由引理4得
,由引理4得
 (14)
(14)
(13)和(14)与(12)矛盾。
情况2取 ,使对
,使对
 (15)
(15)
则 。事实上,若
。事实上,若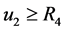 ,由引理2(iv)和引理4得
,由引理2(iv)和引理4得
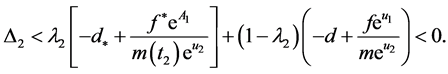 (16)
(16)
若 ,由引理2(v)和引理4得
,由引理2(v)和引理4得
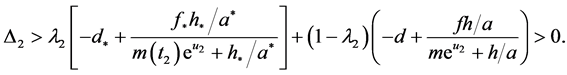 (17)
(17)
(16)和(17)与(15)矛盾。于是当 时,
时,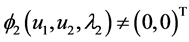 。引理5证毕。于是
。引理5证毕。于是

引理6.如果 ,则
,则
 (18)
(18)
证明记 。注意到
。注意到
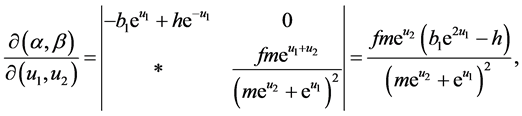
所以 。由(11)的第一个方程
。由(11)的第一个方程 ,得
,得
 . (19)
. (19)
若 ,由(18),(19)得
,由(18),(19)得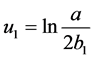 。于是由
。于是由 得
得 。这里
。这里 ,所以(18)成立,引理6证毕。
,所以(18)成立,引理6证毕。
注意1.考虑到引理4的代数方程,假设 且
且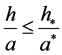 ,定理1不再需要其他条件。
,定理1不再需要其他条件。
基金项目
国家自然科学基金资助项目,项目批准号:60672085;山东省本科高校教学改革研究项目,项目批准号:2015M139。
文章引用
卓相来,张丰雪. 具收获项和周期系数的广义捕食-被捕食模型的正周期解题
Positive Periodic Solutions for a Generalized Prey–Predator Model[J]. 应用数学进展, 2017, 06(03): 308-316. http://dx.doi.org/10.12677/AAM.2017.63036
参考文献 (References)
- 1. 李永昆. 中立型捕食者—被捕食者系统的周期正解[J]. 应用数学和力学, 1999, 20(5): 545-550.
- 2. Zhang, Z.Q. and Wang, Z.C. (2004) The Existence of a Periodic Solution for a Generalized Prey-Predator System with Delay. Mathematical Proceedings of the Cambridge Philosophical Society, 137, 475-486. https://doi.org/10.1017/S0305004103007527
- 3. Zhang, Z.Q. (2005) Periodic Solutions of a Predator-Prey System with Stage-Structures for Predator and Prey. Journal of Mathematical Analysis and Applications, 30, 291-305. https://doi.org/10.1016/j.jmaa.2003.11.033
- 4. Zhang, Z.Q. and Zeng, X.W. (2005) Periodic Solutions of a Nonautonomous Stage-Structured Single Species Model with Diffusion. Quarterly of Applied Mathematics, 63, 277-289. https://doi.org/10.1090/S0033-569X-05-00947-5
- 5. 马知恩. 种群生态学的数学建模与研究[M]. 合肥: 安徽教育出版社, 1996.
- 6. Arditi, R. and Ginzburg, L.R. (1989) Coupling in Predator-Prey Dynamics: Ratio-Dependence. Journal of Theoretical Biology, 139, 311-326. https://doi.org/10.1016/s0022-5193(89)80211-5
- 7. Berryman, A.A. (1992) The Origins and Evolution of Predator-Prey Theory. Ecology, 73, 1530-1535. https://doi.org/10.2307/1940005
- 8. Fan, M., Wang, Q. and Zou, X. (2003) Dynamics of a Non-Autonomous Ratio-Dependent Predator-Prey System. Proceedings of the Royal Society of Edinburgh Section A: Mathematics, 133, 97-118. https://doi.org/10.1017/S0308210500002304
- 9. Tian, D.S. and Zeng, X.W. (2005) Existence of at Least Two Periodic Solutions of a Ratio-Dependent Predator-Prey Model with Exploited Term. Acta Mathematicae Applicatae Sinica (English Series), 21, 489-494.
- 10. Gaines, R.E. and Mawhin, J.L. (1977) Coincidence Degree and Non-linear Differential Equations. Springer, Berlin. https://doi.org/10.1007/BFb0089537
- 11. Zhuo, X.-L., and Zhang, F.-X. (2017) Stability for a New Discrete Ratio-Dependent Predator-Prey System. Qualitative Theory of Dynamical Systems, 1-14. https://doi.org/10.1007/s12346-017-0228-1