Pure Mathematics
Vol.
09
No.
03
(
2019
), Article ID:
30137
,
7
pages
10.12677/PM.2019.93042
Finite Abelian Group with Automorphism Group for Order
Jingjing Shi, Fang Zhou*
Department of Mathematics, Taiyuan Normal University, Jinzhong Shanxi
*通讯作者。

Received: Apr. 16th, 2019; accepted: Apr. 27th, 2019; published: May 9th, 2019

ABSTRACT
In this paper, according to the character of finite Abelian group G and the order of automorphism group of it, the structure of finite Abelian group G with automorphism group for the order
is discussed. The following results are obtained: G has 6 types when t = 1; G has 22 types when t = 2; G has 49 types when t = 3.
Keywords:Finite Abelian Group, Automorphism, Structure of Group

自同构群的阶为
的有限Abel群G
石静静,周芳*
太原师范学院数学系,山西 晋中

收稿日期:2019年4月16日;录用日期:2019年4月27日;发布日期:2019年5月9日

摘 要
本文利用有限Abel群G的性质和它的自同构群的阶,讨论了自同构群
的阶为
的有限Abel群G的构造。得出以下结果:当t = 1时,G最多有6型;当t = 2时,G最多有22型;当t = 3时, 最多有49型。
关键词 :有限Abel群,自同构群,群构造

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
众所周知,自同构群
是由群G决定的。反之,如果知道
的阶,能否确定群G的构造?余红宴和黄本文在这方面做了一些研究,见 [1] [2] [3] 。本文将讨论当
的阶为
时,群G的构造。文中设群G是有限Abel群,
表示群G的阶,
表示群G的自同构群,
表示n阶的循环群,而
表示群G的Sylow
子群,其它符号是标准的,见文献 [4] 。
2. 预备知识
引理2.1 [4] 若
,则
为
阶的交换群,其中
为欧拉函数。
引理2.2 [4] 若G是
阶交换群,则
。
引理2.3 [4] 设
,则当
时,
。
引理2.4 [5] 设G是
阶交换群,G的型为
,其中
,,则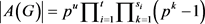 ,其中
,其中
下面在定理的证明中,总假定
为不同的奇素数。
3. 主要结果及证明
定理3.1设 为有限交换群,当
(p,q为互异的奇素数)时,群G最多有6型。
证明:设
,则
,并且
。由于对每个奇素数
来说,都有
,而
,则有
,所以
。
(1) 当
时,
。又
,而
,故
。
(I) 当
时,
,则
,进而
,与
矛盾。
(II) 当
时,
,则
,。
(i) 若
,有
,与
矛盾。
(ii) 若
,有
,与
矛盾。
(2) 当
时,由于
,得
,则有
。又由
,而
,故
。
(I) 当
时,则有
,我们有
,。由于
,可得
。当
为素数时,有
,。
(II) 当
时,则
,。
(i) 若
,有
,。因为
,令
,即
。当
为素数时,有
,。同理,令
,即
,当
为素数时,有
,。
(ii) 若
,则有
,,此时
,与
矛盾,故G不存在。
定理3.2设G为有限交换群,当
(p,q为互异的奇素数)时,群G最多有22型。
证明:设
,则有
,且
。由于对每一个奇素数
,有
,而且
,所以
,故
。
(1) 当
时,
。由于
,且
,可得
。
(I) 当
时,由定理3.1的证明可知,G是不存在的。
(II) 当
时,
,则
。
(i) 若
,有
。
(ii) 若
,有
。
(iii) 若
,有
。均与
矛盾。
(2) 当
时,
,由
可知,
,则
。
(I) 当
时,我们有
,并且
,故
。
(i) 当
时,有
,此时
,得出
。当
为素数时,有
,。
(ii) 当
时,可知
。
(a) 若
,则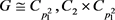 。由于
,若令
,即
。当
为素数时,有
,。同理,令
,有
,。
。由于
,若令
,即
。当
为素数时,有
,。同理,令
,有
,。
(b) 若
,则有
,而
,与
矛盾,因此G不存在。
(II) 当
时,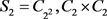 。
。
(i) 当
时,
。
(a) 若
,有
,由于
,可得
。当
为素数时,有
。
(b) 若
,有
,因为
,可令
,则有
。当
为素数时,有
。
(ii) 当
时,
。
(a) 若
,则有
。
若
,此时
。若令
,则
。当
为素数时,有
。同理,令
时,有
。
若
,由于
,得
,矛盾,故G不存在。
(b) 若
,此时
。
若
,由于
,则有
,此时得到
,与
为不同的奇素数矛盾,因此G不存在。
若
,由
,我们有
,矛盾,故G不存在。
(3) 当
时,
,又
,所以
。由
,可得
,。
(I)
:
,此时有
。由于
是不同的偶数,而
,则当
为素数时,有
, ;当
为素数时,有
,。
(II)
:此时只需考虑
。由于
,若令
,则有
。由于
是不同的偶数,而
,则当
为素数时,有
,,,。同理,令
时,有
,,,。
(III)
:只需考虑
,由
,可得
,与
为互异的奇素数不符,故G不存在。
定理3.3 设G为有限交换群,当
(p,q为互异的奇素数)时,群G最多有49型。
证明:设
,则有
,以及
。由于对每个奇素数
,有
,而
,所以
,因此可得
。
(1) 当
时,
。又因为
,而
,所以
。
(I) 当
时,由定理3.2的证明知,G不存在。
(II) 当
时,
,则
。
(i) 若
,则有
与
不符。
(ii) 若
,由计算可知均有
矛盾,故G不存在。
(2) 当
时,
,因为
,可知
,则
。
(I) 当
时,由于
,而又有
,故
。
(i) 当
时,
,此时
,得到
。当
为素数时,有
,。
(ii) 当
时,可知
。
(a) 若
,有
,此时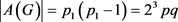 。若令
,即
。当
为素数时,有
,。同理,令
时,有
,。
。若令
,即
。当
为素数时,有
,。同理,令
时,有
,。
(b) 若
,则有
。由
,若
, 为偶数时,产生矛盾。
为奇数时,代入等式左边为偶数,右边为奇数,不符,因此G不存在。
(II) 当
时,
。
(i) 当
时,
。
(a) 若
,有
,由
,得出
。当
为素数时,有
。
(b) 若
,则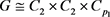 ,此时
。若
,可知
。当
为素数时,有
。
,此时
。若
,可知
。当
为素数时,有
。
(ii) 当
时,
。
(a) 若
,可知
。
当
,由
,得
。若令
,即
。当
为素数时,有
。同理,令
时,有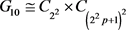 。
。
当
,由
,得
,产生矛盾,故G不存在。
(b) 若
,有
,。
当
,我们有
,从而
。若令
,则
,于是有
。
当
,则有
,于是
,产生矛盾,因此G不存在。
(III) 当
时,
。当
时,由前面的证明易知G不存在,所以只需考虑
。
(i) 当
时,
,有
。由于
,可得
,从而
。当
为素数时,有
。
(ii) 当
时,
,同样也只考虑
,于是
,此时
,可得
。若令
,即
,当
为素数时,有
。同理,令
时,有
。
(3) 当
时,
,又因为
,所以
。由
,得出
,。
(I) 当
时,
(i)
:此时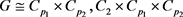 ,于是
。由于
是不同的偶数,而
。所以当
为素数时,有
, ;当
为素数时,有
, ;当
为素数时,有
, ;当
为素数时,有
,。
,于是
。由于
是不同的偶数,而
。所以当
为素数时,有
, ;当
为素数时,有
, ;当
为素数时,有
, ;当
为素数时,有
,。
(ii)
:只需考虑
,于是有
。由于
是不同的偶数,若
,则
,而
。所以当
为素数时,有 ,
,, ;当
为素数时,有
,,,。同理,若令
,则当
为素数时,有
,,, ;当
为素数时,有
,,,。
,
,, ;当
为素数时,有
,,,。同理,若令
,则当
为素数时,有
,,, ;当
为素数时,有
,,,。
(iii)
:我们只需考虑
,由
,可得
,,则有
,。
(II) 当
时,
。
(i) 当
时,
(a) 若
,有
,从而
,进而
。由于
是不同的偶数,而
。所以当
为素数时,有
;当
为素数时,有
。
(b) 若
,有
,从而
,进而
。若令
,则有
,而
。所以当
为素数时,有
。
(ii) 当
时,
(a) 若
,我们有
,从而
,进而
。若
,则
,而
。当
为素数时,有
, ;同理,若令
,则有
,。
(b) 若
,有
。由于
,从而
。此时
,与
为互异的奇素数不符,故G不存在。
(iii) 当
时,
(a) 则
,于是
,可得
。此时
,与
为不同的奇素数矛盾,所以G不存在。
(b) 有
,此时
,从而可得
,矛盾,所以G不存在。
(4) 当
时,我们有
。
(I)
:此时
,从而
,而
。所以当
为素数时,有
,。
(II)
:此时
,从而
。令
,而
,此时
,,产生矛盾,因此G不存在。同理,
时,G也是不存在的。
(III)
:有
。由于
,此时得到
,与
为互异的奇素数不符,从而G不存在。
(IV)
:有
,此时
,产生矛盾,故G不存在。
4. 结束语
本文讨论了自同构群的阶为
的有限Abel群G的构造,得出:当t = 1时,G最多有6型;当t = 2时,G最多有22型;当t = 3时,G最多有49型。
基金项目
国家自然科学基金(11401424)资助项目资助。
文章引用
石静静,周 芳. 自同构群的阶为2tpq(1≤t≤3)的有限Abel群G
Finite Abelian Group with Automorphism Group for Order 2tpq(1≤t≤3)[J]. 理论数学, 2019, 09(03): 316-322. https://doi.org/10.12677/PM.2019.93042
参考文献
- 1. 余红宴, 黄本文.自同构群的阶为2tp2q(t=1,2,3)的有限Abel群G [J]. 数学杂志, 2010, 30(5): 883-890.
- 2. 余红宴. 自同构群的阶为2tp2(p为奇素数)的有限Abel群G [J]. 信阳师范学院学报(自然科学版), 2011, 24(3): 287-291.
- 3. 黄本文.|A(G)|=2tpqr(1≤t≤3)的有限Abel群G的构造[J]. 武汉大学学报(自然科学版), 1993(2): 9-13.
- 4. 张远达. 有限群构造(上、下册) [M]. 北京: 科学出版社, 1982.
- 5. 俞曙霞. 有限交换p-群的自同构群的阶的几点注记[J]. 数学杂志, 1983(2): 189-194.








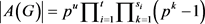 ,其中
,其中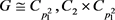 。由于
,若令
,即
。当
为素数时,有
,。同理,令
,有
,。
。由于
,若令
,即
。当
为素数时,有
,。同理,令
,有
,。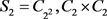 。
。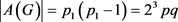 。若令
,即
。当
为素数时,有
,。同理,令
时,有
,。
。若令
,即
。当
为素数时,有
,。同理,令
时,有
,。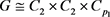 ,此时
。若
,可知
。当
为素数时,有
。
,此时
。若
,可知
。当
为素数时,有
。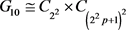 。
。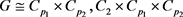 ,于是
。由于
是不同的偶数,而
。所以当
为素数时,有
, ;当
为素数时,有
, ;当
为素数时,有
, ;当
为素数时,有
,。
,于是
。由于
是不同的偶数,而
。所以当
为素数时,有
, ;当
为素数时,有
, ;当
为素数时,有
, ;当
为素数时,有
,。 ,
,, ;当
为素数时,有
,,,。同理,若令
,则当
为素数时,有
,,, ;当
为素数时,有
,,,。
,
,, ;当
为素数时,有
,,,。同理,若令
,则当
为素数时,有
,,, ;当
为素数时,有
,,,。