Advances in Applied Mathematics
Vol.
10
No.
05
(
2021
), Article ID:
42446
,
7
pages
10.12677/AAM.2021.105161
(2 + 1)维Sawada-Kotera方程波的态转换
庞燕敏
华北电力大学,北京
收稿日期:2021年4月17日;录用日期:2021年5月2日;发布日期:2021年5月20日

摘要
本文研究了(2 + 1)维Sawada-Kotera方程的转换动力学特性。通过Hirato双线性方法和复数化参数,我们给出孤立波解和一阶呼吸波解。基于转换条件,我们得到了几种转换波,包括(振荡) W型或M型孤子、和多峰孤子。接着,我们研究了转换波的时变性质。
关键词
(2 + 1)维Sawada-Kotera方程,态转换,时变性质
State Transition of the Wave for (2 + 1)-Dimensional Sawada-Kotera Equation
Yanmin Pang
North China Electric Power University, Beijing
Received: Apr. 17th, 2021; accepted: May 2nd, 2021; published: May 20th, 2021

ABSTRACT
Under investigation in this work is the (2 + 1)-dimensional Sawada-Kotera equation. By the Hirato bilinear method and complex parameters, we give the solitary-wave solution and the first-order breath-wave solution. Based on the transition condition, we obtained the transformed waves, including the (oscillating) M- and W-shaped solitons and multi-peak solitons. Next, we investigate the time-varying features.
Keywords:(2 + 1)-Dimensional Sawada-Kotera Equation, State Transition, Time-Varying Property

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
众所周知,所有可积方程都有孤子解,这反映了自然界中一种常见的非线性现象 [1]。孤立子 [2] [3] [4] [5] 理论的研究对非线性偏微分方程有重要意义。近来,越来越多的研究者已经注意到精确解的研究,如有理解、怪波解和呼吸波解 [6] [7] [8] [9] [10],它们可以在某些方向上指数地定位解。研究已经发现许多可积方程具有精确解,例如KP方程 [11],非线性薛定谔方程 [12] 和Boussinesq方程 [13]。本文研究的是(2 + 1)维Sawada-Kotera方程
(1)
它由Konopelchenko和Dubrovsky首次提出 [14],其中u是变量x,y,t的函数。
本文的结构如下:
第2章给出了几种转换波。首先,我们推导出(2 + 1)维Sawada-Kotera方程的孤立波解和一阶呼吸波解。然后,我们利用转换条件得到转换波。第3章研究了方程(1~2)的转换波的时变性质。通过分析孤立波源和周期波源的相移,我们发现叠加区域随时间而变化,这导致了转换波形状的变化。第4章为结论。
2. 转换波
首先,我们给出以下变换 [1]
(2)
其中, 是一个未知的实函数。将方程(2)代入方程(1),得到双线性式 [1]:
(3)
其中, 和 表示Hirota双线性算子被定义为 [15]
它的N-孤立波解为
(4)
其中,
(5)
和 是自由常数。
考虑 ,取 和 为复常数,即
(6)
其中, 表示复共轭, 和 是实值的。把上式代入(4),我们得到 为
(7)
其中,
(8)
(9)
(10)
(11)
(12)
我们把方程(7)带入方程(4)得到呼吸波解
(13)
呼吸波解由双曲函数以及三角函数组成。双曲函数和三角函数分别决定孤立波源和周期波源的行为。因此,呼吸波可以被认为是它们的非线性组合。当波数满足
即
(14)
此时,呼吸波发展成了另一种叫做转换波的波。在这种情况下,方程(7)中的函数 被改写为
(15)
其中,
(16)
(17)
(18)
(19)
我们将方程(15)代入方程(4)得到转换波解的表达式为
(20)
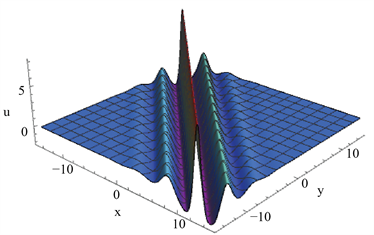
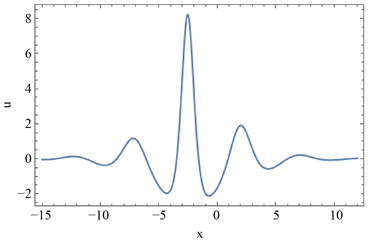
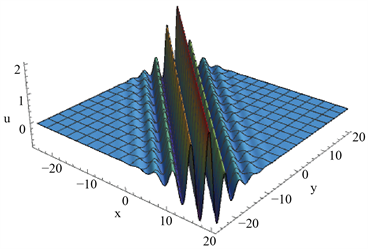
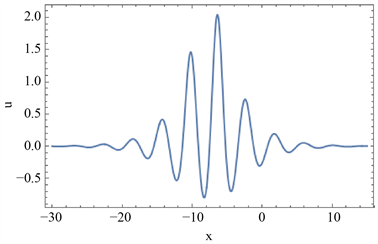
当参数满足一定的物理条件时,转换波可以被展示为M型孤子(见图1)、振荡W型(M型)孤子(见图2,图3)、多峰孤子(见图4)。(a)表示几种转换波的三维结构,(b)表示它们在y = 0处的截面图。
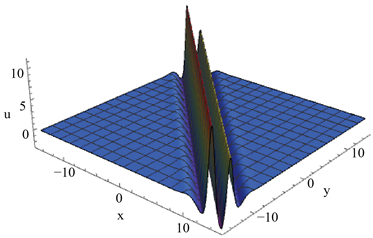 (a)
(a)
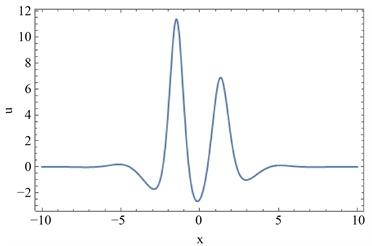 (b)
(b)
Figure 1. M-shaped soliton. The parameters are
图1. M型孤子。参数为
 (a)
(a)
 (b)
(b)
Figure 2. The oscillating W-shaped soliton. The parameters are
图2. 振荡W型孤子。参数为 。
 (a)
(a)
 (b)
(b)
Figure 3. Theoscillating M-shaped soliton. The parameters are
图3. 振荡M型孤子。参数为
 (a)
(a)
 (b)
(b)
Figure 4. The multi-peak soliton. The parameters are
图4. 多峰孤子。参数为
3. 时变性质
转换波的孤立波源和周期波源的相位如下
(21)
(22)
它们之间的相位差是
与时间变量t有关。因此,这些转换波的形状随时间而变化。
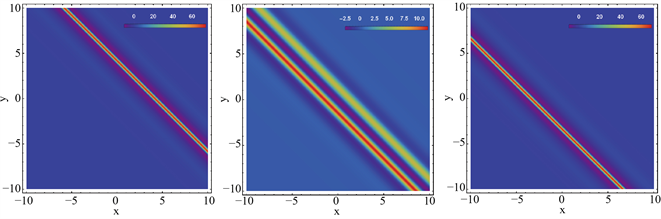
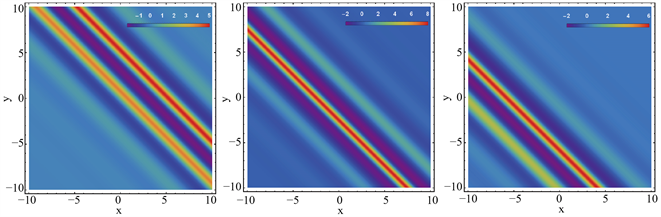
本节介绍W型或M型孤子和振荡W型或M型孤子的时变性质。图5(a)~(c)是M型或W型孤子在三个不同时刻的密度图。图5(d)是它们在三个不同时刻的截面图,从中我们看到W型孤子和M型孤子交替变换。图6(a)~(c)是振荡M型或振荡W型孤子在三个不同时刻的密度图。图6(d)是它们在三个不同时刻的截面图,从中我们看出转换波有明显的时变性质。
 (a) (b) (c)
(a) (b) (c)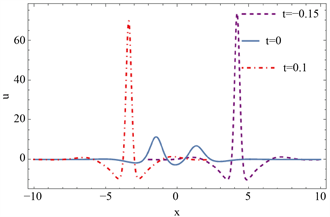 (d)
(d)
Figure 5. The time-varying property of M-shaped solitons
图5. M型孤子的时变性质
 (a) (b) (c)
(a) (b) (c)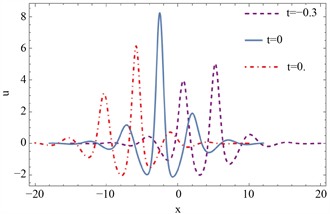 (d)
(d)
Figure 6. The time-varying property of oscillating W-shaped solitons
图6. 振荡W型孤子的时变性质
4. 结论
本文研究了(2 + 1)维Sawada-Kotera方程的不同类型的转换波,包括M型孤子(见图1)、振荡W型或M型孤子(见图2和图3)和多峰孤子(见图4)。另外,我们讨论了几种转换波的时变性质(见图5和图6)。我们发现叠加区域随时间而变化,这造成转换波发生形变。
致谢
本文作者衷心感谢审稿人的意见和建议。
文章引用
庞燕敏. (2 + 1)维Sawada-Kotera方程波的态转换
State Transition of the Wave for (2 + 1)-Dimensional Sawada-Kotera Equation[J]. 应用数学进展, 2021, 10(05): 1515-1521. https://doi.org/10.12677/AAM.2021.105161
参考文献
- 1. Chen, Y., Huang, L.L., et al. (2017) Lump Solutions and Interaction Phenomenon for (2 + 1)-Dimensional Sawada-Kotera Equation. Communications in Theoretical Physics, 67, 473. https://doi.org/10.1088/0253-6102/67/5/473
- 2. 李翊神. 孤子与可积系统[M]. 上海: 上海科技教育出版社, 1999.
- 3. 黄景宁, 徐济仲, 熊吟涛. 孤子: 概念、原理和应用[M]. 北京: 高等教育出版社, 2004.
- 4. 陈登远. 孤子引论[M]. 北京: 科学出版社, 2006.
- 5. 広田良吾, 王红艳, 李春霞, 等. 孤子理论中的直接方法[M]. 北京: 清华大学出版社, 2008.
- 6. Akhmediev, N., Ankiewicz, A. and Taki, M. (2009) Waves That Appear from Nowhere and Disappear without a Trace. Physics Letters A, 373, 675-678.
- 7. Osborne, A.R. (2010) Nonlinear Ocean Waves and the Inverse Scattering Transform. Academic Press Inc., Cambridge.
- 8. Kuznetsov, E.A. (1977) Solitons in Parametrically Unstable Plasma. Doklady Akademiinauk SSSR, 22, 507-508.
- 9. Falcon, É., Laroche, C. and Fauve, S. (2002) Observation of Depression Solitary Surface Waves on a Thin Fluid Layer. Physical Review Letters, 89, Article ID: 204501. https://doi.org/10.1103/PhysRevLett.89.204501
- 10. Pelinovsky, D.E., Stepanyants, Y.A. and Kivshar, Y.S. (1995) Self-Focusing of Plane Dark Solitons in Nonlinear Defocusing Media. Physical Review E, Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics, 51, 5016-5026. https://doi.org/10.1103/PhysRevE.51.5016
- 11. Manakov, S.V., Zakharov, V.E., Bordag, L.A., et al. (1977) Two-Dimensional Solitons of the Kadomtsev-Petviashvili Equation and Their Interaction. Physics Letters A, 63, 205-206. https://doi.org/10.1016/0375-9601(77)90875-1
- 12. Peregrine, D.H. (1983) Water Waves, Nonlinear Schrdinger Equations and Their Solutions. The ANZIAM Journal, 25, 16-43. https://doi.org/10.1017/S0334270000003891
- 13. Ma, H.C. and Deng, A.P. (2016) Lump Solution of (2 + 1)-Dimensional Boussinesq Equation. Communications in Theoretical Physics, 65, 546-552. https://doi.org/10.1088/0253-6102/65/5/546
- 14. Konopelchenko, B.G. and Dubrovsky, V.G. (1984) Some New Integrable Nonlinear Evolution Equations in 2+1 Dimensions. Physics Letters A, 102, 15-17. https://doi.org/10.1016/0375-9601(84)90442-0
- 15. Hirota, R. (2004) The Direct Method in Soliton Theory. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511543043