基于相似结构的算法设计 Algorithms Design Based on Similar Structure

doi:10.12677/AAM.2013.23014

设为首页加入收藏期刊导航网站地图

期刊菜单

文章导航

Advances in Applied Mathematics 应用数学进展, 2013, 2, 107-113

http://dx.doi.org/10.12677/aam.2013.23014 Published Online August 2013 (http://www.hanspub.org/journal/aam.html)

Algorithms Design Based on Similar Structure

Congyin Fan, Shunchu Li, Xiaoxu Dong, Lixia Bai

Institute of Applied Mathematics, Xihua University, Chengdu

Email: fcy8843@163.com

Received: Jun. 20th, 2013; revised: Jun. 29th, 2013; accepted: Jul. 8th, 2013

permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract: Based on the similar structure theory, we conduct a rigorous mathematical derivation and prove the

solution procedure of a class of differential equation boundary value problems. Thus, we put forward a new

algorithm to solve this kind of boundary value problem—Similar Structure Algorithm. As the similar struc-

ture algorithms only have four arithmetic and logical operations, they are easily available for the computer.

An example was given at the end of this paper. Also a simulation experiment was designed by using MAT-

LAB programming language according to the proposed algorithms. By changing the coefficients of the

boundary conditions, results are observed and analyzed.

Keywords: MATLAB Programming; Algorithms Design; Simulation Experiment; Similar Structure

基于相似结构的算法设计

范聪银，李顺初，董晓旭，白丽霞

西华大学应用数学研究所，成都

Email: fcy8843@163.com

收稿日期：2013 年6月20 日；修回日期：2013 年6月29 日；录用日期：2013 年7月8日

摘要：基于相似结构理论，本文对一类微分方程边值问题的求解过程进行严谨的数学推导和证明；

由此提出解决这类边值问题的一种新算法——相似结构算法。相似结构算法仅仅只包含四则运算和逻

辑运算，所以该算法很容易面向计算机。在文章最后，列举一个例子，根据本文所设计出来的算法利

用MATLAB 语言编写程序作仿真实验，且通过改变边界条件的系数来观察和分析实验结果的变化。

关键词：MATLAB 程序；算法设计；仿真实验；相似结构

1. 引言

对于一个给定的数值问题或非数值问题可以有许多种不同的算法去解决它，这些算法都能给出近似答案，

但所需的计算量和得到的精确程度可能相差很大。而判断一个算法的优劣主要看这个算法是否能面向计算机，

是否有可靠理论分析，同时还要考虑计算的复杂程度。2001 年，李庆扬等提出了有关数值问题算法的理论基础[1]。

2010 年李雪峰提出了在云计算环境下的web 数据挖掘算法研究，该研究为原先的算法提供了可靠的理论分析和

提高了算法的精度[2]。2006~2012 年，万海平等在不同环境下对HITS 算法进行了改进，这些研究不仅降低了原

算法的复杂程度而且也为该类算法提供了可靠的理论分析[3-7]。

事实上，算法的设计是基于数学思想的。而一种优异的数学思想对于设计一个好的算法有着很重要的导向。

2004 年李顺初教授首先发表了第一篇关于微分方程边值问题解的具有相似结构的文章[9]。随后 2010年严娟等证

范聪银等  基于相似结构的算法设计

明了含参数 λ的Bessel 方程边值问题的解具有相似结构[10]。黄荣军，王芙蓉等于 2012~2013年在相结构思想的

基础上分别提出了关于求第一种 Weber方程和Airy 方程边值问题的解的相似构造法[11,12]。文献[9-12]的研究共

同证实了一个结论：解式作为数与图形的桥梁，它也具有某种相似的结构—可以表示为连分式的乘积形式，这

为设计新的算法提供了新的思路。

本文研究针对如下二阶线性齐次微分方程的边值问题

 





ypxyqxy

EyEF yD

Gy Hy



 







 











;

(1)

的求解进行研究，其中均为已知的常数，且

,,,, ,,DEFGHab 22

0, 0,DGH a



 

；已知函数













,,pxCab qx2

,C ab。不失一般性，假设知道目标方程的两个线性无关解，并用这两个解来构造引解

函数；其次求边值问题(1)在非齐次左边值条件为一种特殊情形下的解，得到相似核函数(用引解函数和齐次右边

值条件中的系数表示出来)；再次求出边值问题(1)的解(用相似核函数和非齐次左边值条件中的系数组装得到)。

最后根据边值问题(1)的解设计出求该类边值问题解的一个新算法——相似算法。本文给出一个具体例子

(Thomson方程边值问题)，根据所设计出来的算法利用MATLAB[13]语言编写程序作仿真实验，并且通过改变实

例中的右边界条件的系数来观察和分析版图的变化，这对于Thomson 方程的边值问题在实际中的应用有重要理

论价值，同时也能体现本文所设计出来算法的可行性。

2. 算法设计的理论前提

假设



x，



x是二阶线性齐次微分方程









0ypxyqxy

 



的两个线性无关的解，作如下四个引

解函数：



















0,01 22 1

,xyxy yxy









(2)

  

1,00,0122 1

,,xxyxyyx



 









(3)

  

0,10,01 22 1

,,xxyxyyxy















 (4)

 

1,10,00,01 22 1

,, ,xxxyxyyx



 











  (5)

3. 算法理论依据

先讨论边值问题(1)的左边界条件的一种特殊情形，它的解将是(1)的解的相似结构中的相似核函数。

定理 1 若边值问题

 



ypxyqxy

Gy Hy



 



















(6)

(参数的限制与(1)中相同)有唯一解，则其解为：











 

0,0 0,1

1,01,1

GxbHxb

GabHab





 

(7)

证明边值问题(6)中目标方程的通解：

范聪银等  基于相似结构的算法设计











112 2

xCyxCyx (8)

其中为任意常数。

,CC

由边值问题(6)中的左边界条件 1

y

可得









1122 1yaC Cya





 (9)

再由边值问题(6)中的右边界条件





Gy Hy 





可得















1112 220CHy bGy bCHybGyb



 

 



(10)

由边值问题(6)有唯一解知，关于待定系数的线性方程组(9)、(10)的系数行列式，结合(3)、(5)

式可求得

,CC 0









1,01,1

,GabHab



 , (11)

利用 Cramer 法则求得

 

122

CHybGyb















(12)

 

211

CHybGy



 b











(13)

把(12)、(13)代入(8)式中，可得边值问题(6)的解：

 













22 11

HybGybHy bGy b

yxyx y







 x







再应用(11)式及(2)、(4)式，可得(7)式。

定理 2 若边值问题(1)有唯一解，则其解为：

  

yD x

EFa

 





(14)

证明同理可知，边值问题(1)中目标方程的通解为(8)式，由(1)中的左边界条件可得



1xa

EyEF yD





 





 

















1112 2

11EyaEFyaCEyaEFyaC



 



2







(15)

再由(1)中的右边界条件





Gy Hy 





，得到(10)式。

因为边值问题(1)有唯一解，所以关于的线性方程组(10)、(15)的系数行列式，结合(3)、(5)式可

求得

,CC 0





 



 

0,00,11,0 1,11,0 1,1

,,,, ,EGabHabFG abH abGabH ab

 









, (16)

利用 Cramer 法则求解线性方程组(10)、(15)得

 

122

CHybGyb













 (17)

 

211

CHybGy



 b









 (18)

将由(17)、(18)式代入(8)式中，可得边值问题(1)的解

 



221 112

yHybGybyxHybGyby



 





x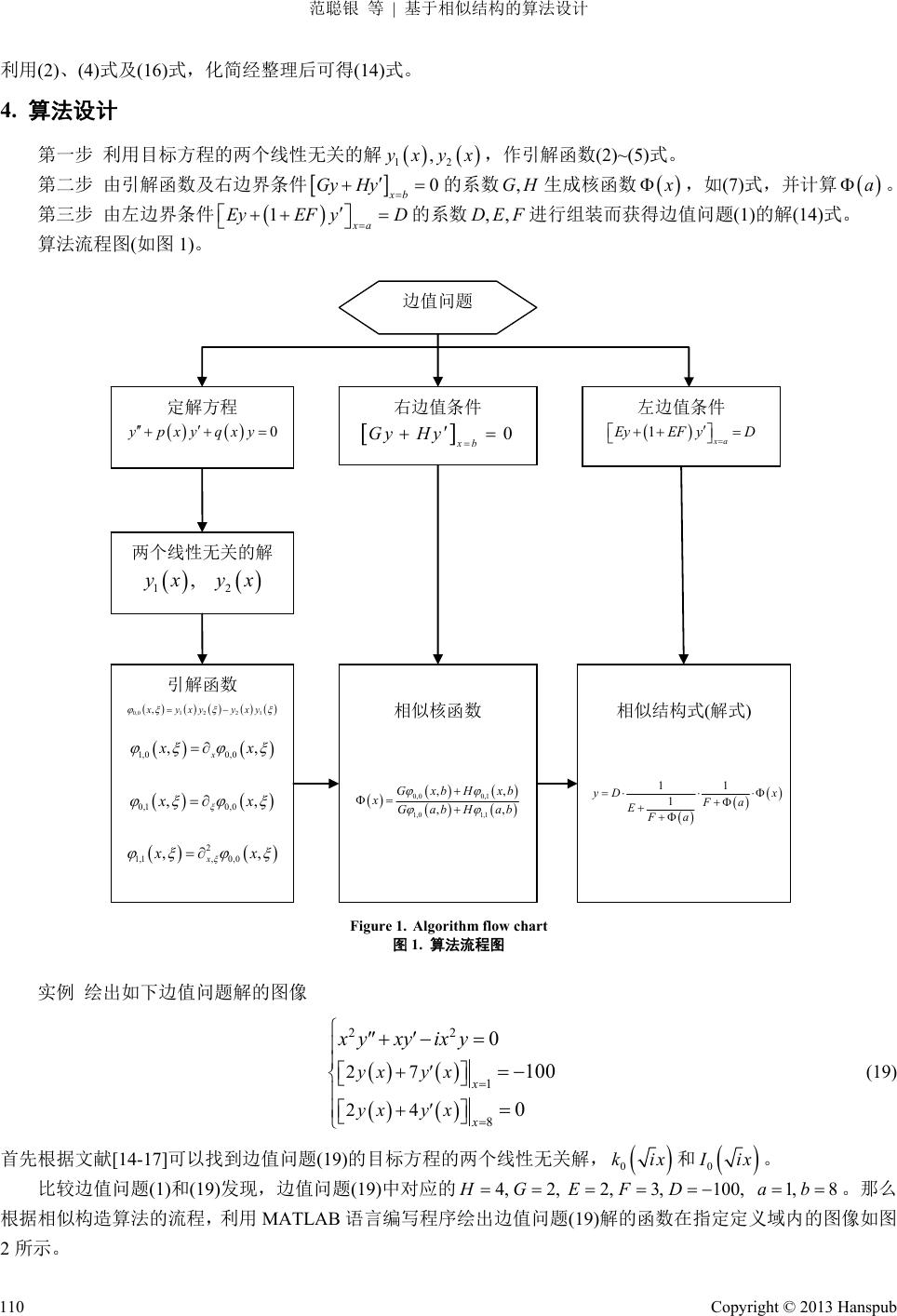

范聪银等  基于相似结构的算法设计

利用(2)、(4)式及(16)式，化简经整理后可得(14)式。

4. 算法设计

第一步利用目标方程的两个线性无关的解









xyx，作引解函数(2)~(5)式。

第二步由引解函数及右边界条件





Gy Hy 





的系数生成核函数,GH





，如(7)式，并计算





a。

第三步由左边界条件的系数进行组装而获得边值问题(1)的解(14)式。



1xa

EyEF yD





 

 ,,DEF

算法流程图(如图 1)。

相似结构式(解式)

  

yD x

EFa

 





边值问题

定解方程









0ypxyqxy

 



两个线性无关的解







,yx yx

引解函数





















0,01 22 1

,xyxyyxy







 

1,0 0,0







 

0,1 0,0









 

1,1, 0,0









相似核函数











 

0,0 0,1

1,0 1,1

GxbHxb

xGabHab





 

左边值条件





1xa

yEFyD











右边值条件





GyHy







Figure 1. Algorithm flow chart

图1. 算法流程图

实例绘出如下边值问题解的图像

 

100

yxyx

xyxy ixy





















 





(19)

首先根据文献[14-17]可以找到边值问题(19)的目标方程的两个线性无关解，





kix和





ix 。

比较边值问题(1)和(19)发现，边值问题(19)中对应的 4, 2,HG



2, 3,100,EFD



1,8ab。那么

根据相似构造算法的流程，利用 MATLAB 语言编写程序绘出边值问题(19)解的函数在指定定义域内的图像如图

2所示。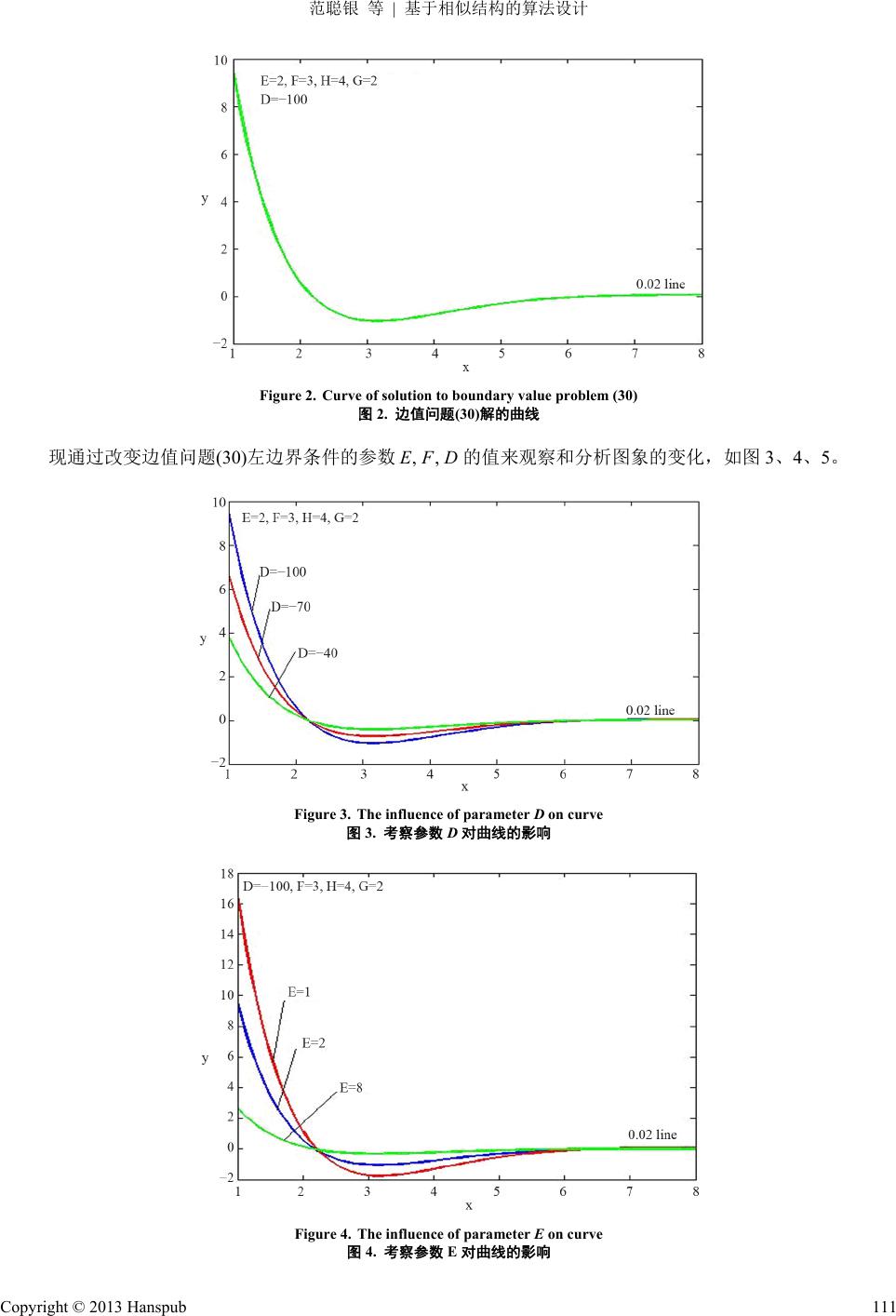

范聪银等  基于相似结构的算法设计

Figure 2. Curve of solution to boundary value problem (30)

图2. 边值问题 (30)解的曲线

现通过改变边值问题(30)左边界条件的参数的值来观察和分析图象的变化，如图 3、4、5。 ,,EFD

Figure 3. The influence of parameter D on curve

图3. 考察参数 D对曲线的影响

Figure 4. The influence of parameter E on curve

图4. 考察参数 E对曲线的影响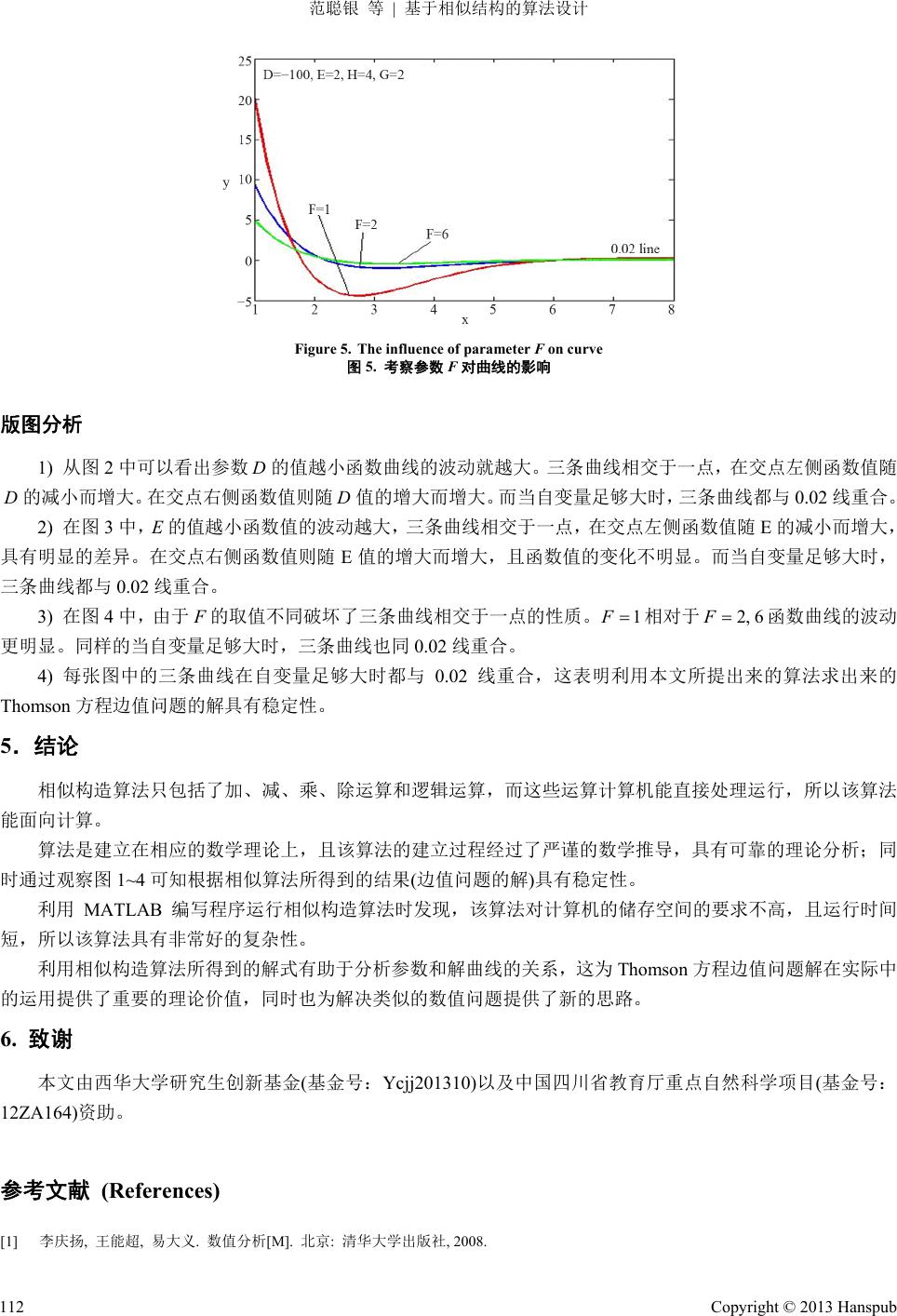

范聪银等  基于相似结构的算法设计

Figure 5. The influence of parameter F on curve

图5. 考察参数 F对曲线的影响

版图分析

1) 从图 2中可以看出参数的值越小函数曲线的波动就越大。三条曲线相交于一点，在交点左侧函数值随

的减小而增大。在交点右侧函数值则随值的增大而增大。而当自变量足够大时，三条曲线都与 0.02 线重合。

D D

2) 在图 3中，E的值越小函数值的波动越大，三条曲线相交于一点，在交点左侧函数值随 E的减小而增大，

具有明显的差异。在交点右侧函数值则随E值的增大而增大，且函数值的变化不明显。而当自变量足够大时，

三条曲线都与0.02 线重合。

3) 在图 4中，由于 F的取值不同破坏了三条曲线相交于一点的性质。 1



相对于函数曲线的波动

更明显。同样的当自变量足够大时，三条曲线也同0.02 线重合。

2, 6F

4) 每张图中的三条曲线在自变量足够大时都与 0.02 线重合，这表明利用本文所提出来的算法求出来的

Thomson 方程边值问题的解具有稳定性。

5．结论

相似构造算法只包括了加、减、乘、除运算和逻辑运算，而这些运算计算机能直接处理运行，所以该算法

能面向计算。

算法是建立在相应的数学理论上，且该算法的建立过程经过了严谨的数学推导，具有可靠的理论分析；同

时通过观察图1~4 可知根据相似算法所得到的结果(边值问题的解)具有稳定性。

利用 MATLAB 编写程序运行相似构造算法时发现，该算法对计算机的储存空间的要求不高，且运行时间

短，所以该算法具有非常好的复杂性。

利用相似构造算法所得到的解式有助于分析参数和解曲线的关系，这为Thomson 方程边值问题解在实际中

的运用提供了重要的理论价值，同时也为解决类似的数值问题提供了新的思路。

6. 致谢

本文由西华大学研究生创新基金(基金号：Ycjj201310) 以及中国四川省教育厅重点自然科学项目(基金号：

12ZA164)资助。

参考文献 (References)

[1] 李庆扬, 王能超, 易大义. 数值分析[M]. 北京: 清华大学出版社, 2008.

范聪银等  基于相似结构的算法设计

[2] 李雪锋. 基于云计算环境的 web 数据挖掘算法研究[J]. 北京交通大学学报, 2010, 30(2): 30-33.

[3] 万海平, 何华灿, 周延泉. HITS 算法的改进[J]. 山东大学学报(理学版), 2006, 41(2): 17-20.

[4] 邓超, 何月顺. 基于 web 结构挖掘的 HITS 算法分析及改进[J]. 湖南农机, 2011, 38(1): 80-82.

[5] 谢海艇. 基于锚文本的HITS 算法研究[J]. 内蒙古科技与经济, 2009, 12(190): 28-30.

[6] 郭鸿. 一种基于文本内容的 H ITS 改进算法[J]. 计算机系统应用, 2009, 18(9): 38-42.

[7] 李昕, 朱永胜, 武港山. Web 结构分析算法 HITS 的改进及应用[J]. 计算机工程, 2005, 31(6): 40-43.

[8] 马瑞新, 邓贵仕, 王晓. 基于扩散理论的 HITS 算法在 web 挖掘中的研究与优化[J]. 计算机应用研究, 2012, 29(1): 145-147.

[9] S. C. Li, M. H. Jia. The formal similarity of solutions on the class of differential equation[J]. 电子科技大学学报, 2004, 33(增刊): 95-98.

[10] 迟颖, 李顺初, 严娟. 含参数λ的Bessel 方程边值问题的相似结构[J]. 大连交通大学学报, 2010, 31(5): 109-111.

[11] 黄荣军, 李顺初, 许东旭. 求解第一种Weber 方程边值问题的相似构造法[J]. 绵阳师范学院学报, 2012, 31(11): 1-5(-15).

[12] 王芙蓉, 李顺初, 许东旭. Airy 方程的一类边值问题的解的相似构造法[J]. 湖北师范学院学报(自然科学版), 2013, 33(1): 79-85.

[13] 龚纯, 王正林. MATLAB 语言常用算法程序集[M]. 北京: 电子工业出版社, 2008.

[14] 溪定平. Bessel function[M]. 北京: 高等教育出版社, 1998.

[15] 刘式适, 刘式达. 特殊函数[M]. 北京: 气象出版社, 2002.

[16] 李顺初, 黄柄光. Laplace 变换与Bessel 函数及试井分析理论基础[M]. 北京: 石油工业出版社, 2000: 8.

[17] N. H. Asmar. Partial differential equations with Fourier series and boundary value problems. Upper Saddle River: Prentice Hall, 2005.