 Hans Journal of Civil Engineering 土木工程, 2013, 2, 232-239 http://dx.doi.org/10.12677/hjce.2013.24040 Published Online September 2013 (http://www.hanspub.org/journal/hjce.html) Based on the Experiment of Saturated Water Concrete Fatigue Life’s Finite Element Analysis Yongcheng Sun1, Gang Wang1, Xuemin Wang2 1China IPPR International Engineering Corporation, Beijing 2Gen China Holdings Co., Ltd., Tianjin Email: sunyongcheng2002@163.com Received: Apr. 1st, 2013; revised: May 10th, 2013; accepted: May 28th, 2013 Copyright © 2013 Yongcheng Sun et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Abstract: Based on the experiment, the paper gets saturated water concrete’s Double logarithm fatigue equation. The article uses nonlinear finite element software ANSYS, combines with engineering instances, obtains the relationship between the panel thickness, frequency and fatigue life and lays the foundation for the further study. Keywords: Double Logarithm Fatigue Equation; Fatigue, Saturated Water Concrete; Finite Element 基于试验基础的饱和水混凝土疲劳寿命有限元分析 孙永成 1,王 刚1,王学敏 2 1中国中元国际工程公司,北京 2融创中国控股股份有限公司,天津 Email: sunyongcheng2002@163.com 收稿日期:2013 年4月1日;修回日期:2013年5月10 日;录用日期:2013 年5月28 日 摘 要:本文在试验的基础上得出饱和水混凝土的双对数疲劳方程,并且利用非线性有限元 ANSYS 软件,结 合工程实例进行了分析,得出了实际工程中面板厚度、疲劳次数和寿命的关系,为下一步的深入研究打下了基 础。 关键词:双对数疲劳方程;疲劳;饱和水混凝土;有限元 1. 引言 在工程应用中,混凝土结构处承受静荷载外还承 受多次循环动荷载作用,并且循环动荷载如风荷载、 波浪荷载等所占的比例相对增大,这些结构在重复荷 载作用下,很有可能产生疲劳破坏,所以深入研究疲 劳寿命意义非常深远。 2. 试验材料、参数的选取及试验方法 2.1. 试验材料及参数的选取 本实验采用标准实验试件,即150 mm × 150 mm × 550 mm。水泥采用普通硅酸盐水泥,混凝土强度 C30,其配合比如表 1所示。在本次混凝土的弯曲疲 劳试验中,疲劳荷载上限的应力水平分别取为 0.900、 0.800、0.750、0.675、0.600 和0.550,即疲劳荷载的 上限值分别为 0.900 f 抗折 、0.800 f 抗折 、0.750 f 抗折 、 0.675 f 抗折 、0.600 f 抗折 和0.550 f 抗折 ,疲劳荷载的 Table 1. The concrete mixture proportion 表1. 混凝土配合比 水 水泥 砂 1~3碎石 0.5~1碎石 153 368 6530 1043 259 Copyright © 2013 Hanspub 232  基于试验基础的饱和水混凝土疲劳寿命有限元分析 下限值取为 0.1 f 抗折 。 2.2. 试验方法 实验前先检查试件,如试件中部l/3 长度内有蜂 窝(如直径大于7 mm × 2 mm),该试件应立即作废, 否则应在记录中注明。在试件中部量出其宽度和高 度,精确到 1 mm。然后调整两个可移动支座,使其 与实验机 PMS—500D 疲劳试验机下压头中心距离各 为150 mm,将试件置于支座上如图1、2所示[1]。 3. 试验结果 混凝土试块疲劳试验结果如表2、3所示。 表2可以看出,混凝土的疲劳寿命数据的离散性 很大。因此,只有在详细地研究各种不同应力水平情 况下疲劳寿命的规律之后,才能比较准确的,全面的 了解和掌握混凝土疲劳的规律。首先在不同应力水平 下考虑失效概率时的疲劳寿命的威布尔分布规律,并 Figure 1. The fatigue experiment under the level of stress under the level of stress 图1. 应力水平下的疲劳实验 Figure 2. The destruction map under fatigue load 图2. 疲劳破坏图 Table 2. The concrete fatigue test data sheet 表2. 混凝土疲劳实验数据表 应力水平 试件编号 0.900 0.800 0.750 0.675 0.600 1 37 535 7161 20,402 561,243 2 50 668 9403 83,719 918,231 3 53 1028 10,286 84,718 976,835 4 70 2920 11,169 87,364 1,015,872 5 72 3533 11,668 107,5071,085,700 6 80 3915 13,876 109,0781,201,474 7 123 4464 17,905 114,1412,116,598 Table 3. The result of regression analysis with experimental data 表3. 实验数据回归分析结果 应力水平 Smax 回归系数 b 回归系数 blnNa 相关系数 R 0.600 3.599779 24.457427 0.96590 0.675 3.028736 15.287192 0.95800 0.750 7.560868 31.555050 0.95000 0.800 6.885070 24.359980 0.97778 0.900 5.453900 10.362070 0.96750 计算出 和lg i N1 lnln p 的值[2]。然后将实验数据回 归分析整理的结果表 3。 从以上五种应力水平下威布尔分布拟合的方程 中各数值的相关系数很高(R 值均在0.95 以上),所以 可以表明, 1 lnln p 与 是线性相关的,而且线 lg i N 性相关的程度很高。 由回归分析整理过程中计算公式可以计算得出 不同应力水平下威布尔疲劳寿命预测值如表 4所示。 根据表 4中的疲劳寿命预测值和可靠度值整理得 到单对数 值[3],数据列于表5。 lg i N 将表 4、表 5按照公式 进行一元 线性回归,回归分析结果如表 6所示。 lg lglgSab 从表 6中可以看出:不同可靠度下威布尔分布拟 合的方程中的相关系数均在0.97 以上可以看出:1) 与应力水平 是成线性关系的,说明假设线性 关系是成立的,并且线性相关的程度很高; 2) 失效概 率(可靠度)对回归系数 b的影响很小,因此可以忽略 不计,通常情况下取 b的平均值作为通用结果。 lg Nlg S 饱和水混凝土的双对数疲劳方程为[4]: lg0.0385lg lgSNa (1) Copyright © 2013 Hanspub 233  基于试验基础的饱和水混凝土疲劳寿命有限元分析 Copyright © 2013 Hanspub 234 Table 4. The predictions of fatigue life of Weibull distribution under the different level of stress and failure probability 表4. 不同应力水平不同失效概率下威布尔分布的疲劳寿命预测值 应力水平 可靠度 0.900 0.800 0.750 0.675 0.600 10% 113 4563 19,221 210,260 1,061,292 20% 97 4047 17,235 160,143 8,440,050 30% 85 3673 15,777 128,432 7,009,919 40% 77 3353 14,518 104,350 5,886,566 50% 68 3053 13,335 84,401 4,924,136 60% 60 2758 12,151 66,927 4,050,839 70% 51 2445 10,892 50,933 3,219,289 80% 42 2090 9442 35,657 2,384,905 90% 31 1626 7513 20,155 1,475,727 95% 23 1278 6034 11,660 931,198 Table 5. The logarithms predictions of fatig ue life of Weibull distri bu t ion under the different level of stress and failure probability 表5. 不同应力水平不同失效概率下威布尔分布的疲劳寿命对数预测值 应力水平 可靠度 0.900 0.800 0.750 0.675 0.600 10% 7.025837 5.322756 4.283778 3.659224 2.052862 20% 6.926345 5.204507 4.236410 3.607206 1.987194 30% 6.845713 5.108672 4.198020 3.565048 1.933973 40% 6.769862 5.018519 4.161907 3.525390 1.883908 50% 6.692331 4.926371 4.124994 3.484854 1.832736 60% 6.607545 4.825599 4.084627 3.440525 1.776773 70% 6.507760 4.707000 4.037118 3.388353 1.710911 80% 6.377471 4.552147 3.975087 3.320233 1.624916 90% 6.169006 4.304378 3.875836 3.211240 1.487321 95% 5.969042 4.066712 3.780631 3.106691 1.355337 Table 6. The double logarithmic result of regression analysis 表6. 双对数回归分析结果 可靠度 回归系数 b 回归系数lga 相关系数R 10% 0.03735 0.0218 0.9885 20% 0.0377 0.0200 0.9970 30% 0.03798 0.01897 0.9960 40% 0.03823 0.01793 0.9940 50% 0.0385 0.01680 0.9940 60% 0.03878 0.01552 0.9920 70% 0.0391 0.01392 0.9886 80% 0.03953 0.01237 0.9885 90% 0.03993 0.01077 0.9858 95% 0.03997 0.00921 0.9760 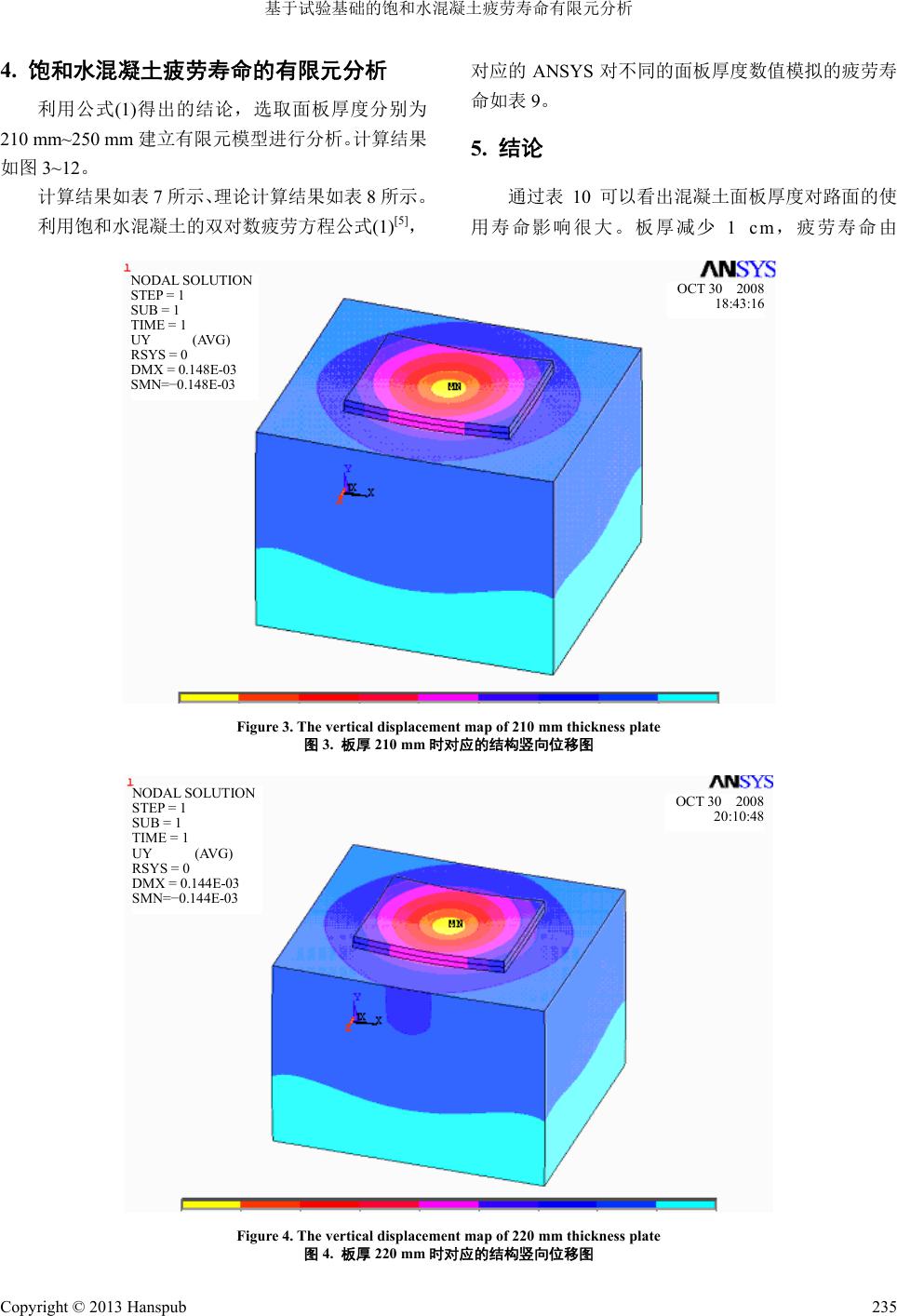 基于试验基础的饱和水混凝土疲劳寿命有限元分析 4. 饱和水混凝土疲劳寿命的有限元分析 利用公式(1)得出的结论,选取面板厚度分别为 210 mm~250 mm建立有限元模型进行分析。计算结果 如图 3~12。 计算结果如表7所示、理论计算结果如表 8所示。 利用饱和水混凝土的双对数疲劳方程公式(1)[5], 对应的 ANSYS对不同的面板厚度数值模拟的疲劳寿 命如表 9。 5. 结论 通过表 10 可以看出混凝土面板厚度对路面的使 用寿命影响很大。板厚减少 1 cm,疲劳寿命由 N ODAL SOLUTION STEP = 1 SUB = 1 TIME = 1 UY (AVG) RSYS = 0 DMX = 0.148E-03 SMN=−0.148E-03 OCT 30 2008 18:43:16 Figure 3. The vertical displacement map of 210 mm thickness plate 图3. 板厚 210 mm时对应的结构竖向位移图 N ODAL SOLUTION STEP = 1 SUB = 1 TIME = 1 UY (AVG) RSYS = 0 DMX = 0.144E-03 SMN=−0.144E-03 OCT 30 2008 20:10:48 Figure 4. The vertical displacement map of 220 mm thickness plate 图4. 板厚 220 mm时对应的结构竖向位移图 Copyright © 2013 Hanspub 235  基于试验基础的饱和水混凝土疲劳寿命有限元分析 N ODAL SOLUTION STEP = 1 SUB = 1 TIME = 1 UY (AVG) RSYS = 0 DMX = 0.140E-03 SMN=−0.140E-03 OCT 31 2008 08:16:49 Figure 5. The vertical displacement map of 230 mm thickness plate 图5. 板厚 230 mm时对应的结构竖向位移图 N ODAL SOLUTION STEP = 1 SUB = 1 TIME = 1 UY (AVG) RSYS = 0 DMX = 0.136E-03 SMN=−0.136E-03 OCT 31 2008 08:27:05 Figure 6. The vertical displacement map of 240 mm thickness plate 图6. 板厚 240 mm时对应的结构竖向位移图 OCT 31 2008 21:24:34 N ODAL SOLUTION STEP = 1 SUB = 1 TIME = 1 UY (AVG) RSYS = 0 DMX = 0.132E-03 SMN=−0.132E-03 Figure 7. The vertical displacement map of 250 mm thickness plate 图7. 板厚 250 mm时对应的结构竖向位移图 Copyright © 2013 Hanspub 236  基于试验基础的饱和水混凝土疲劳寿命有限元分析 N ODAL SOLUTION STEP = 1 SUB = 1 TIME = 1 S1 (AVG) DMX = 0.148E-03 SMN=−453388 SMX=112952 OCT 30 2008 18:47:21 Figure 8. The 1st principal stress map of 210 mm thickness plate 图8. 板厚 210 mm时对应的结构第一主应力图 Figure 9. The 1st principal stress map of 220 mm thickness plate 图9. 板厚 220 mm时对应的结构第一主应力 Figure 10. The 1st principal stress map of 230 mm thickness plate 图10. 板厚 230 mm时对应的结构第一主应力 Copyright © 2013 Hanspub 237 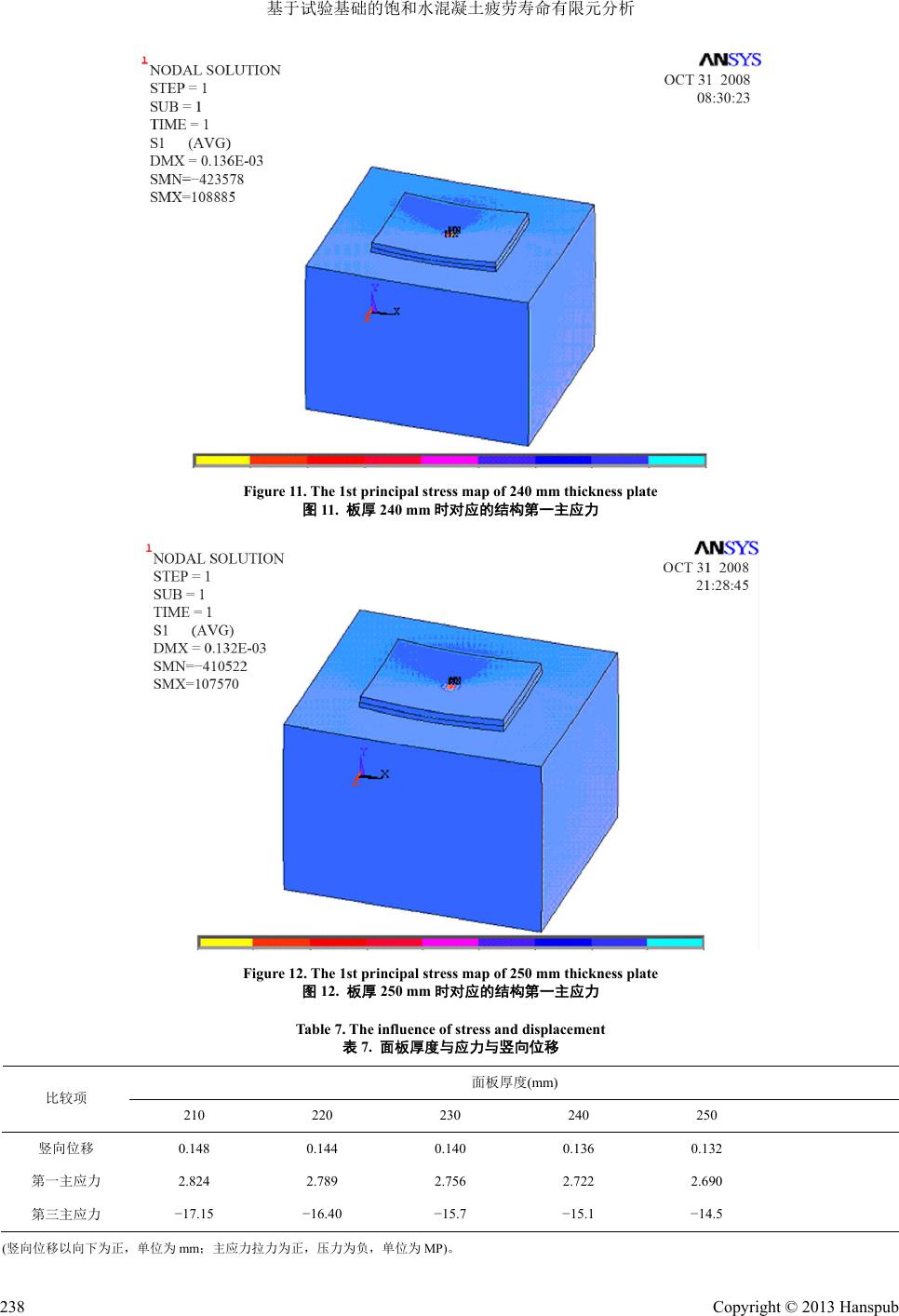 基于试验基础的饱和水混凝土疲劳寿命有限元分析 Figure 11. The 1st principal stress map of 240 mm thickness plate 图11. 板厚240 mm时对应的结构第一主应力 Figure 12. The 1st principal stress map of 250 mm thickness plate 图12. 板厚 250 mm时对应的结构第一主应力 Table 7. The influence of stress and displacement 表7. 面板厚度与应力与竖向位移 面板厚度(mm) 比较项 210 220 230 240 250 竖向位移 0.148 0.144 0.140 0.136 0.132 第一主应力 2.824 2.789 2.756 2.722 2.690 第三主应力 −17.15 −16.40 −15.7 −15.1 −14.5 (竖向位移以向下为正,单位为 mm;主应力拉力为正,压力为负,单位为 MP)。 Copyright © 2013 Hanspub 238  基于试验基础的饱和水混凝土疲劳寿命有限元分析 Copyright © 2013 Hanspub 239 Table 8. The theory calculation of fatigue life 表8. 理论计算疲劳寿命值 面板厚度(mm) 比较项 210 220 230 240 250 疲劳寿命 1.82 7.41 20 37.11 58.83 Table 9. The valve of parameter for fatigue 表9. S-N疲劳性能参数值 N 1E2 2E2 1E3 5E3 1E4 5E4 S/MPa 0.870563 0.847638 0.79671 0.748841 0.729122 0.685134 N 1E5 2E5 5E5 1E6 1.5E6 2E6 S/MPa 0.667268 0.649696 0.627176 0.610661 0.601202 0.594580 Table 10. The influence of fatigue life with different plates thickness 表10. 面板厚度对路面疲劳寿命的影响 面板厚度(mm) 比较项 210 220 230 240 250 疲劳寿命(次数) 0.138576E + 06(次) (1.9 年) 0.583926E + 06(次) (8.0 年) 0.1509E + 07(次) (20.7年) 0.27886E + 07(次) (38.2年) 0.44311 + 07(次) (60.7年) 20.7 年减少到了 8.0 年;减少2 cm,疲劳寿命由20.7 年减少到了 1.9 年;而板厚增加 1 cm,疲劳寿命由 20.7 年增加到了 38.2年;增加 2 cm,疲劳寿命增加到了 60.7 年。由此可见,面层板厚对水泥混凝土路面结构 疲劳使用年限的影响是非常显著的。同时,AN SYS 模拟的结果(见表 9)与理论计算的结果(见表8)比较, 其结果误差不超过 10%,从而说明ANSYS 有限元分 析的精确性。 参考文献 (References) [1] 程育仁等. 疲劳强度[M]. 北京: 中国铁道出版社, 1990: 11. [2] 姚明初等. 混凝土在变幅重复应力下疲劳性能的研究[R]. “铁道建筑安全度(可靠性)及设计原理”专题报告, 北京, 1986: 4. [3] 铁道部科学研究院混凝土疲劳研究组. 混凝土在等幅和变幅 重复应力下疲劳性能的研究. 铁道部科学研究院, 1990: 10. [4] 宋玉普, 赵国藩. 钢筋混凝土结构分析中的有限单元法[M]. 大连: 大连理工大学出版社, 1994. [5] 欧进萍, 林燕清. 混凝土高周疲劳损伤的性能劣化实验研究 [J]. 土木工程学报, 1995, 32. |