 Hans Journal of Civil Engineering 土木工程, 2013, 2, 253-258 http://dx.doi.org/10.12677/hjce.2013.25043 Published Online November 2013 (http://www.hanspub.org/journal/hjce.html) Analysis for Dynamic Response of Irregular Structure under Multi-Dimensional Non-Stationary Random Excitations* Mingsheng Fang, Zuoyu Sun#, Hui Wang College of Civil Engineering, Guangzhou University, Guangzhou Email: #sunzuoyu@163.com Received: Sep. 13th, 2013; revised: Oct. 8th, 2013; accepted Oct. 17th, 2013 Copyright © 2013 Mingsheng Fang. This is an open access article distributed under the Creative Commons Attribution License, which permits unre- stricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Abstract: Dynamic responses analysis of an irregular structure under multi-dimensional seismic excitations is studied, in which the seismic excitations are constructed by equivalent excitation method, while the non-stationary features of the input power spectral density both in time domain and frequency domain are considered, and the characteristics of local site are also incorporated in the model. The simulation of a typical frame-tube building is carried out; the results demonstrate that those factors mentioned are very essential to the dynamic responses of the structure. Keywords: Irregular Structure; Dynamic Response; Non-Stationary; Equivalent Excitation 不规则结构在多维非平稳随机激励下的动力响应分析* 方明胜,孙作玉#,王 晖 广州大学土木工程学院,广州 Email: #sunzuoyu@163.com 收稿日期:2013 年9月13 日;修回日期:2013年10 月8日;录用日期:2013 年10月17 日 摘 要:本文着重研究不规则结构在多维地震动激励下的动力响应分析,基于等效激励法构造了多维地震动激 励,考虑了随机激励功率谱在时域和频域上的非平稳性,同时模型中也考虑了场地等因素的影响。对一个典型 的框架–筒体不规则结构进行了数值仿真,结果表明同时考虑激励的非平稳特性和多维激励对结构的动力响应 至关重要。 关键词:不规则结构;动力响应;非平稳;等效激励法 1. 引言 随着现代建筑结构技术的发展,高耸大跨等结构 日益增多,同时由于对建筑美学和实际应用的功能需 求,不规则结构也得到了广泛的应用,如国家歌剧院、 中央电视台总部大楼、上海证券大厦等。对于这类结 构,详细地分析其在多维地震激励作用下动力响应具 有十分重要的科学意义和工程价值。近年来,国内外 学者在此方面做了一系列的探讨,取得了诸多研究成 果[1-3],但多数局限于单维地震激励分析或者平稳随机 震动分析,同时考虑激励的非平稳特性和多维激励对 结构的动力响应的影响并不多见。而真实地震激励往 往是多维、非平稳的,并和建筑所在场地以及震中距 等诸多因素有关。李宏男进行了多维地震激励的研 究,但没有考虑激励的非平稳特性[4]。林家浩在传统 理论的基础上提出了虚拟激励法[5],大大提高了计算 效率和精度,但并没有解决激励的非平稳特性。孙作 *基金项目:国家自然科学基金资助项目(51178127)。 #通讯作者。 Open Access 253  不规则结构在多维非平稳随机激励下的动力响应分析 玉在虚拟激励法的基础上提出了等效激励法[6],进一 步地提高了计算效率,并考虑了激励能量的在时域上 的非平稳特性,但忽略掉了随机激励中振动能量随频 率分布的非平稳性。为此,他进一步提出了考虑双非 平稳性的等效地震动激励的构造方法[7],即基于等效 激励法,运用连续小波变换理论构造了多维等效非平 稳演变随机地震激励,实现了随机激励的能量在时域 和频域上的非平稳性。本文采用了这种方法,构造了 多维地震动激励,同时考虑场地特性、震中距、震级 等因素的影响,更真实地模拟了实际地震波。对一个 典型的不规则结构进行了数值仿真分析,探讨了这些 因素对结构动力响应的影响。 2. 多维非平稳激励的构造 2.1. 等效非平稳随机激励的构造 结构受地震、强风等随机激励作用往往持续时间 较短,以至于激励的平稳特性假设不能成立。若再考 虑震中距与震级对地震动特性的影响,这一矛盾将更 加突出。因此施加于建筑结构上的大多数外部激励都 是非平稳的随机过程。由于演变功率谱的复调制函数 难以确定,因此在工程应用和大多数的理论研究中, 往往忽略掉随机激励中振动能量随频率分布的非平 稳性,将实际的双非平稳激励简化为了强度非平稳激 励,这样必然带来计算上的误差。最近孙作玉教授提 出了能同时考虑随机激励的能量在时域和频域上的 双平稳性的等效非平稳演变随机地震激励[7],实现了 激励的双非平稳特性。其主要思路是,基于虚拟激励 法可以构造出虚拟激励 it xx Sgte ,同理可以构 造等效激励 T it xx Sgte d ,运用非平稳功 率谱密度函数 来处理更为真实的情况,通过 连续小波变换同时考虑幅值和相位。其中 a为伸缩因 子,a > 0, , xx S t 为偏移,对 f t进行连续小波变换表达 式如下: ,, * ,, 1d aa Cft tft t t f t a a t (1) 其中*表示复共轭。这个公式进行逆傅里叶变换后: * , 1ˆˆ ,, 2π it a Cfttftaa e 其中 ˆ, f t 和 ˆ 为傅里叶变换的信号和小波。 在逆傅里叶变换中的是时间变量平移参数 t。这 表明我们可以通过逆傅里叶变换对其进行连续小波 变换,其中 ˆ,, i xx f tSte , 。 0, 2π 对于连续小波变换,小波函数必须经过精心挑 选,本文使用 Morelet 函数。在进化功率谱密度中给 出了圆频率、时间、CWT 系数,确定计算的尺度 范 围和位置,小波系数可以采用MATLAB 小波工具箱 函数 sacle2freq 获得。 连续小波变换如下: ,, 2 11 ,d aa ad f tfttt Ca a (3) 其中 2 ˆdC 是可容许条件。 因此,等效激励 f(t)可以很容易通过MATLAB 小 波工具箱函数 icwtft构造,实现了随机激励的能量在 时域和频域上的双平稳性。 2.2. 频谱特性关键参数的影响 强震观测表明,地震发生时,开始阶段高频成分 较强,后来低频成分逐渐增强,最后只剩下低频成分, 这是非均匀调制演变的一个典型例子。因此,本文在 等效随机激励生成以后,考虑其频率分布的非平稳 性,采用非均匀调制函数取 对生成的 激励进行调制。地震波的加速度峰值会在地震波传播 过程中逐渐衰减,其衰减规律与震级、场地土特性和 震中距关系密切。对此,霍俊荣等人进行了全面、系 统的研究,其主要原理是:考虑震级和距离的不确定 性,对大量的地震观察数据进行回归分析,从而获得 某一类型场地上地震峰值加速度与震级 zt gtxt M 和震中距 的衰减规律,同时考虑了场地条件,震级和震中距 的影响。并提出了考虑地震动的近场距离饱和与震级 饱和特性的地震动水平加速度峰值的衰减关系,并与 实际地震的观察数据资料吻合。本文采用其所得的回 归关系[8]: R 6 2 12 34 lg PGAlgCM CCMCMCRe (4) d (2) 其中 PGA 为加速度峰值,R为震级,C1、C2、C3、 Open Access 254 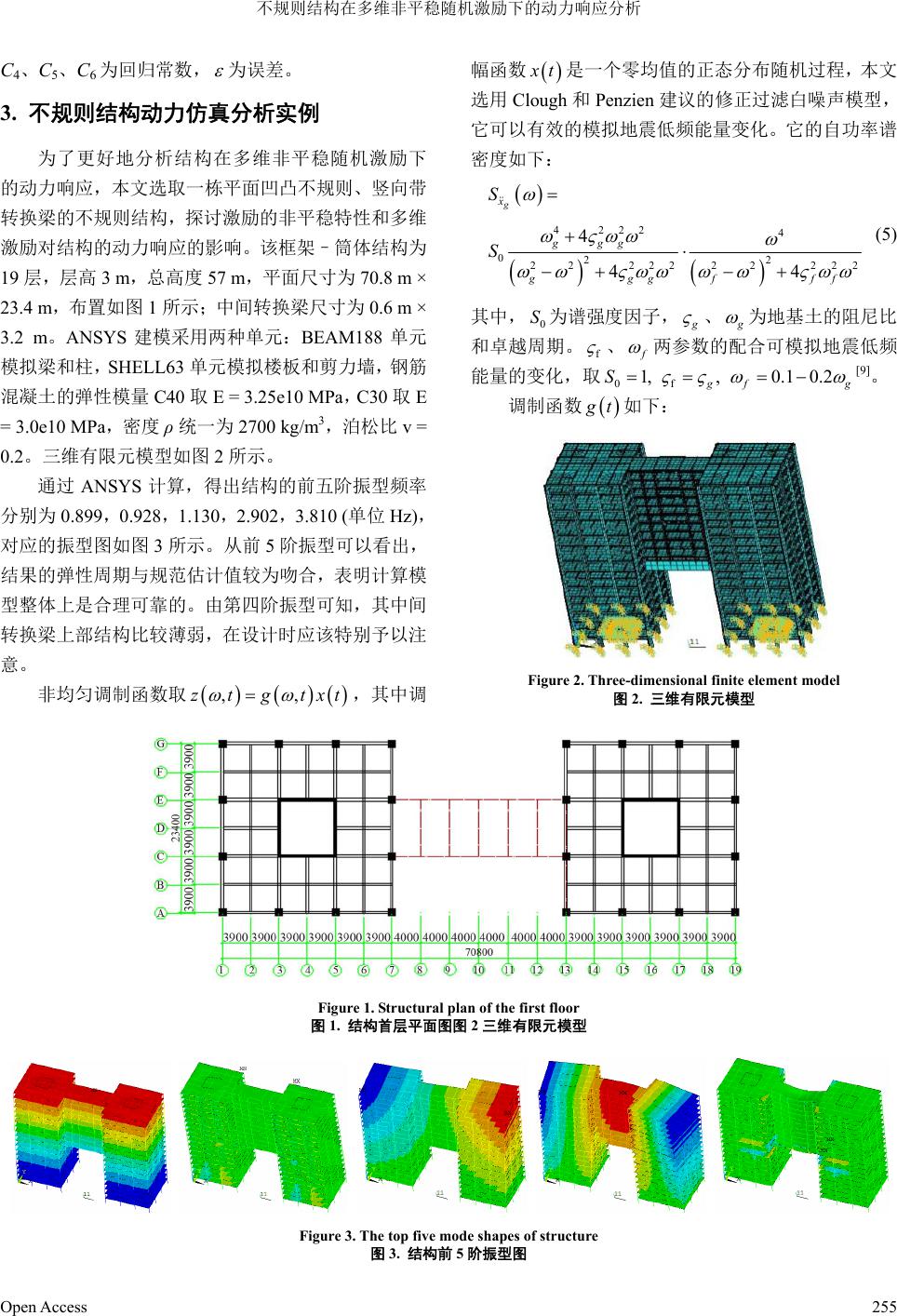 不规则结构在多维非平稳随机激励下的动力响应分析 Open Access 255 幅函数 x t是一个零均值的正态分布随机过程,本文 选用 Clough和Penzien 建议的修正过滤白噪声模型, 它可以有效的模拟地震低频能量变化。它的自功率谱 密度如下: C4、C5、C6为回归常数, 为误差。 3. 不规则结构动力仿真分析实例 为了更好地分析结构在多维非平稳随机激励下 的动力响应,本文选取一栋平面凹凸不规则、竖向带 转换梁的不规则结构,探讨激励的非平稳特性和多维 激励对结构的动力响应的影响。该框架–筒体结构为 19 层,层高 3 m,总高度 57 m,平面尺寸为 70.8 m × 23.4 m,布置如图 1所示;中间转换梁尺寸为 0.6 m × 3.2 m。ANSYS 建模采用两种单元:BEAM188 单元 模拟梁和柱, SHELL63 单元模拟楼板和剪力墙,钢筋 混凝土的弹性模量C40 取E = 3.25e10 MPa,C30 取E = 3.0e10 MPa,密度 ρ统一为2700 kg/m3,泊松比 v = 0.2。三维有限元模型如图 2所示。 4222 4 022 22 22222 222 4 44 g x ggg gggff S S f (5) 其中, 为谱强度因子, 0 S g 、 g 为地基土的阻尼比 和卓越周期。 f 、 f 两参数的配合可模拟地震低频 能量的变化,取0f 0.1 0.21,, g fg S [9]。 调制函数 g t如下: 通过 ANSYS 计算,得出结构的前五阶振型频率 分别为 0.899,0.928,1.130,2.902,3.810 (单位 Hz), 对应的振型图如图 3所示。从前 5阶振型可以看出, 结果的弹性周期与规范估计值较为吻合,表明计算模 型整体上是合理可靠的。由第四阶振型可知,其中间 转换梁上部结构比较薄弱,在设计时应该特别予以注 意。 Figure 2. Three-dimensional finite element model 非均匀调制函数取 ,其中调 ,,ztgtxt 图2. 三维有限元模型 Figure 1. Structural plan of the first floor 图1. 结构首层平面图图 2三维有限元模型 Figure 3. The top five mode shapes of structure 图3. 结构前 5阶振型图 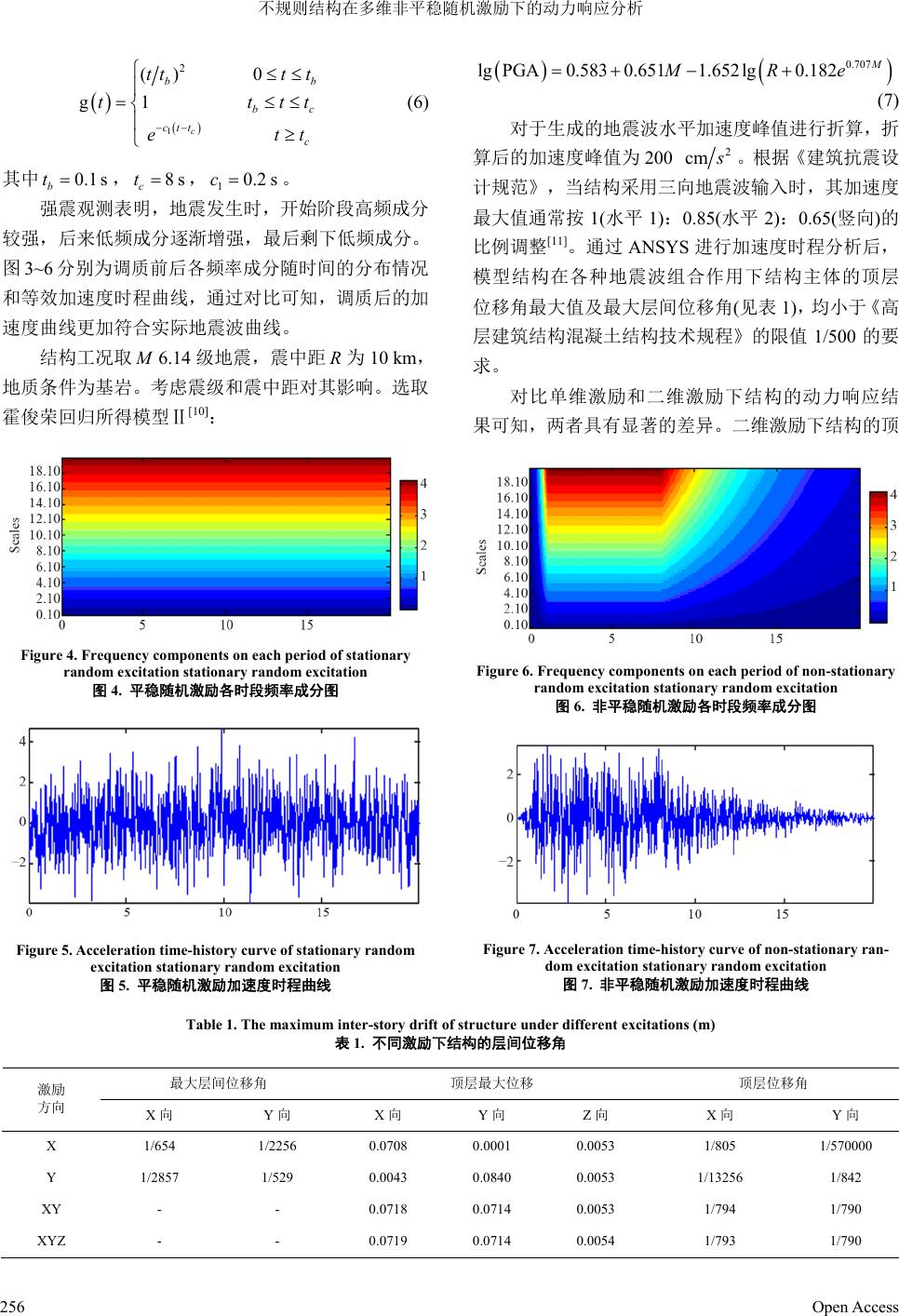 不规则结构在多维非平稳随机激励下的动力响应分析 1 2 () 0 g1 c bb bc ctt c ttt t tt e tt tt (6) 其中, ,0.1 s b t8s c t10.2 sc 。 ,地, 阶段高频成分 较强 强震观测表明震发生时 开始 ,后来低频成分逐渐增强,最后剩下低频成分。 图3~6分别为调质前后各频率成分随时间的分布情况 和等效加速度时程曲线,通过对比可知,调质后的加 速度曲线更加符合实际地震波曲线。 结构工况取 M 6.14 级地震,震中距 R为10 km, 地质考影条件为基岩。 虑震级和震中距对其 响。选取 霍俊荣回归所得模型Ⅱ[10]: Figure 4. Frequency components on each period of stationary random excitation stationary random excitation 图4. 平稳随机激励各时段频率成分图 Figure 5. Acceleration time-history curve of stationary random excitation stationary random excitation 图5. 平稳随机激励加速度时程曲线 0.707 0.583 0.6511.652lg0.182M MRe lg PGA (7 对于生成的地震波水平加速度峰值进行折算, 算后 ) 折 的加速度峰值为 200 2 cm s 。根据《建筑抗震设 计规范》,当结构采用三向 波输入时,其加速度 最大值通常按 1(水平 1):0.85(水平 2):0.65(竖向)的 比例调整[11]。通过 ANSYS 进行加速度时程分析后, 模型结构在各种地震波组合作用下结构主体的顶层 位移角最大值及最大层间位移角(见表 1),均小于《高 层建筑结构混凝土结构技术规程》的限值 1/500 的要 求。 对 地震 比单维激励和二维激励下结构的动力响应结 果可知,两者具有显著的差异。二维激励下结构的顶 Figure 6. Frequency components on each period of non-stationary random excitation stationary random excitation 图6. 非平稳随机激励各时段频率成分图 Figure 7. Acceleration time-history curve of non-stationary ran- inter-story drift of structure under different excitations (m) 最大层间位移角 顶层位移角 dom excitation stationary random excitation 图7. 非平稳随机激励加速度时程曲线 Table 1. The maximum 表1. 不同激励下结构的层间位移角 顶层最大位移 激励 X向 向 X向 YZ向 X向 向 方向 Y向 Y X 1/654 1/2256 0.0708 0.0001 0.0053 1/805 1 /570000 Y 1/2857 1/529 0.0043 0.0840 0.0053 1/13256 1/842 XY - - 0.0718 0.0714 0.0053 1/794 1/790 XYZ - - 0.0719 0.0714 0.0054 1/793 1/790 Open Access 256 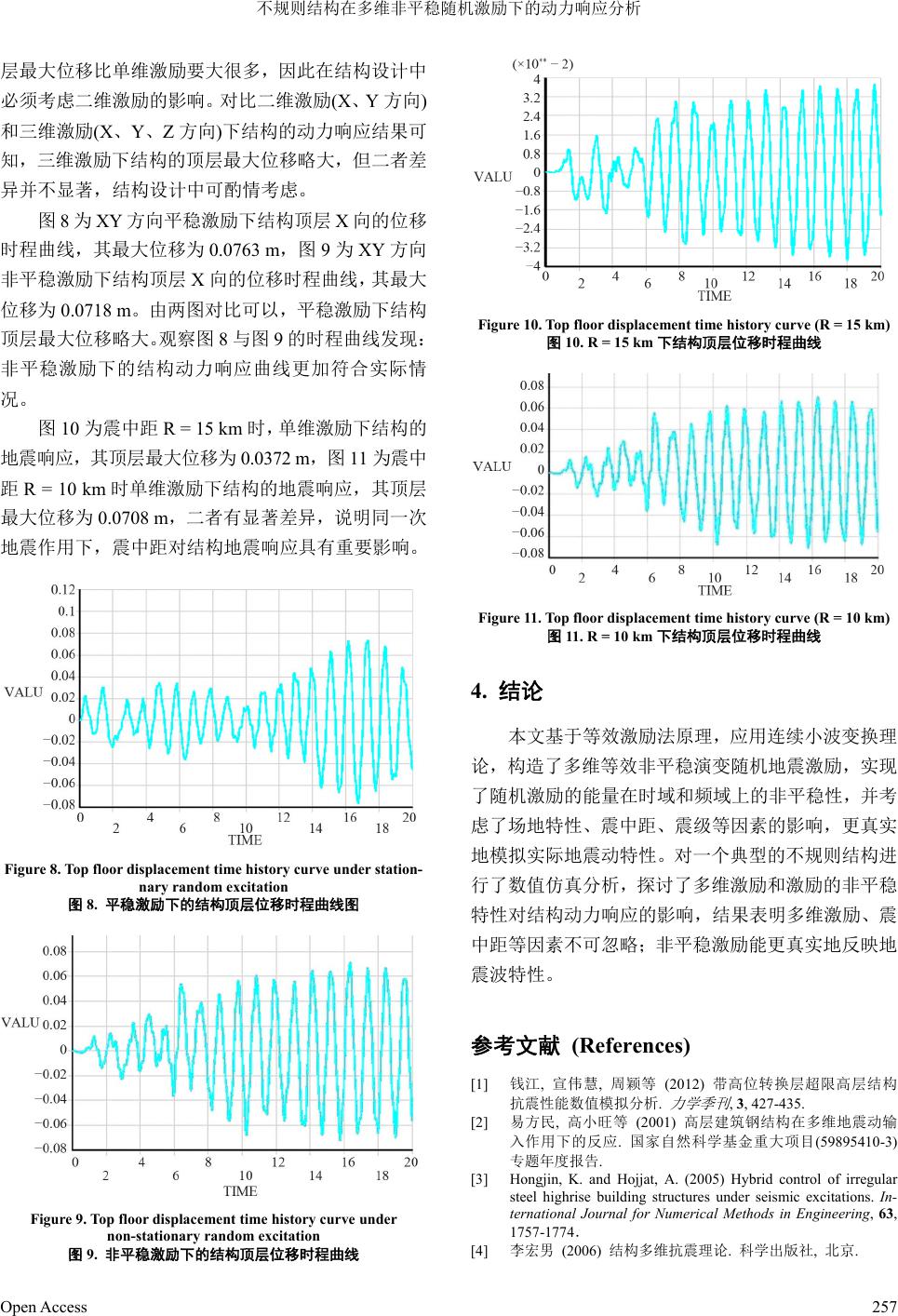 不规则结构在多维非平稳随机激励下的动力响应分析 层最大位移比单维激励要大很多, 此在结构 X向的位移 时程曲线 10 为震中距R = 15 km 时,单维激励下结构的 地震 因 设计中 必须考虑二维激励的影响。对比二维激励(X、Y方向) 和三维激励(X、Y、Z方向)下结构的动力响应结果可 知,三维激励下结构的顶层最大位移略大,但二者差 异并不显著,结构设计中可酌情考虑。 图8为XY 方向平稳激励下结构顶层 ,其最大位移为 0.0763 m,图 9为XY方向 非平稳激励下结构顶层 X向的位移时程曲线,其最大 位移为 0.0718 m。由两图对比可以,平稳激励下结构 顶层最大位移略大。观察图 8与图 9的时程曲线发现: 非平稳激励下的结构动力响应曲线更加符合实际情 况。 图 响应,其顶层最大位移为 0.0372 m,图 11 为震中 距R = 10 km时单维激励下结构的地震响应,其顶层 最大位移为 0.0708 m,二者有显著差异,说明同一次 地震作用下,震中距对结构地震响应具有重要影响。 Figure 8. Top floor displacement time history curve under station- nary random excitation 图8. 平稳激励下的结构顶层位移时程曲线图 Figure 10. Top floor displacement time history curve (R = 15 km) 图10. R = 15 km下结构顶层位移时程曲线 Figure 11. Top floor displacement time history curve (R = 10 km) 图11. R = 10 km下结构顶层位移时程曲线 4. 结论 论,构造了多维等效非平稳演变随机地震激励,实现 的能量在时域和频域上的非平稳性,并考 虑了场地特性、震中距、震级等因素的影响,更真实 地模 慧, 周颖等 (2012) 带高位转换层超限高层结构 抗震性能数值模拟分析. 力学季刊 , 3, 427-435. [2] 易方民, 高小旺等 (2001) 高层建筑钢结构在多维地震动输 学基金重大项目(59895410-3) Hybrid control of irregular gineering, 63, 本文基 法原理,应用连续小波变换理于等效激励 了随机激励 拟实际地震动特性。对一个典型的不规则结构进 行了数值仿真分析,探讨了多维激励和激励的非平稳 特性对结构动力响应的影响,结果表明多维激励、震 中距等因素不可忽略;非平稳激励能更真实地反映地 震波特性。 参考文献 (References) [1] 钱江, 宣伟 入作用下的反应. 国家自然科 专题年度报告. [3] Hongjin, K. and Hojjat, A. (2005) steel highrise building structures under seismic excitations. In- ternational Journal for Numerical Methods in En Figure 9. Top floor displacement time history curve under non-stationary random excitation 图9. 非平稳激励下的结构顶层位移时程曲线 1757-1774. [4] 李宏男 (2006) 结构多维抗震理论. 科学出版社, 北京. Open Access 257  不规则结构在多维非平稳随机激励下的动力响应分析 [5] 林家浩, 张亚辉 (2004) 随机振动的虚拟激励法. 科学出版 H., Fang, M., 2013) c Ex- 生, 曹资 (2003) 基于新抗震规范的地震动随 规律的研究. 中国地震 . 中国建筑工业出 社, 北京, 60. [6] 孙作玉, 王晖 (2010) 结构振动分析的等效激励法. 工程力 学 , S1, 20-22. Sun, Z.Y., Wang, [7] S. et al. ( Random vibr of a Cable-Stayed Bridge under Multi-Dimensional Seismi ation 局工程力学研究所. [11] GB 50011-2001 (2001) 建筑抗震设计规范 citations. Materials Processing and ManufacturingⅢ, 753-755, 1119-1123. [8] 霍俊荣, 胡聿贤 (1992) 地震动峰值参数衰减规律的研究. 地震工程与工程震动 , 1992, 2, 1-11. [9] 薛素铎, 王雪 机模型参数研究. 土木工程学报 , 5, 5-10. [10] 霍俊荣 (1989) 近场强地面运动衰减 版社, 北京, 2. Open Access 258 |