 Advances in Applied Mathematics 应用数学进展, 2013, 2, 165-170 http://dx.doi.org/10.12677/aam.2013.24022 Published Online November 2013 (http://www.hanspub.org/journal/aam.html) The Solitary Loop Wave Solution of a CH-KP Equation Dexiang Zhao Xinping Second Middle School, Yuxi Email: xshaml@yxnu.net Received: Aug. 12th, 2013; revised: Sep. 6th, 2013; accepted: Sep. 19th, 2013 Copyright © 2013 Dexiang Zhao. This is an open access article distributed under the Creative Commons Attribution License, which per- mits unrestricted u s e , distribution, and reproduction in any medium, provided the original work is properly c it ed . Abstract: The solitary loop wave of a CH-DK equation is investigated by using the dynamical system theory. The existence conditions of solitary loop wave are found and the explicit parametric function expressions of solitary loop wave are given in this article. Keywords: CH-KP Equation; Travelling Wave Equation; Equilibrium Point; Solitary Loop Wave 一个 CH-KP 方程的孤立圈波 赵德祥 新平第二中学,玉溪市 Email: xsham l@yxnu.net 收稿日期:2013 年8月12 日;修回日期:2013 年9月6日;录用日期:2013 年9月19 日 摘 要:用微分方程动力系统方法研究一个 CH-KP 方程发现 CH-KP 方程存在孤立圈波。给出了孤立 圈波的存在条件,得到了孤立圈波的精确参数函数表达式。 关键词:CH-KP 方程;行波方程;平衡点;孤立圈波 1. 引言 文献[1]研究了 CH-KP 方程的行波结构及性质。 2 mn tx xyy xxt x ukuuauu u 0 (1) 在一些特定的条件下,文献[1]给出了方程(1)的一些光滑和非光滑行波解。文献[2]用拟孤立波方法得到了方 程(1)的1-孤立波解。对任意 m、n,计算方程(1)的行波很困难,因此在m = 2、n = 1,和 a < 0的条件下,本文 用动力系统分支方法[1,3,4]研究方程(1),发现方程(1)存在孤立圈波,并计算出孤立圈波的精确参数形式解。 2. 行波方程 2, 1mn 时,方程(1)可写为 2 2 tx xyy xxt x ukuuauu u 0 (2) 作变换 ,,uxyt 、 x yct ,方程(2)变为 Open Access 165  赵德祥 一个 CH-KP 方程的孤立圈波 2 2kc ca 0 (3) 对方程(3)积分两次,第一次积分取0为积分常数,第二次积分以g为积分常数,得行波方程 22 21 2 a kcc g (4) 设z ,方程(4)变为2维平面系统 2 d d 21 2 d2 d2 z akcg cz z c 2 (5) 令 d2dc (6) 系统(6)变为 22 d2 d d21 2 d2 cz za kcg cz (7) 明显地,系统(5)和(7)有同样的首次积分 2243 2 22 1 ,2 43 kc a H zcz g h (8) 设 2 1 21 2 kc ga (9) 2 2 42 1 9 kc ga (10) 2 1 21212 , kckc ag g gc a (11) 根据平面微分方程动力系统关于平衡点的结论知系统(7)的平衡点有下列性质: 1) 时, 0gc 0, 2 g c 是2个鞍点; 2) 1 g g时,21 ,0 kc a 是1个尖点; 3) 时, 和 是2个中心点; 0, 0gc ,0 ,0 4) 时,和是 2个鞍点; g0, 0c ,0 ,0 5) 时, 是1个中心点, 10,0,21 0gg ckc ,0 ,0 是1个鞍点; 6) 时, 1个鞍点, 10,0,21 0gg ckc ,0 ,0 是1个中心点; 7) 时, 是1个鞍点, 10,0,21 0gg ckc ,0 ,0 是1个中心点; Open Access 166 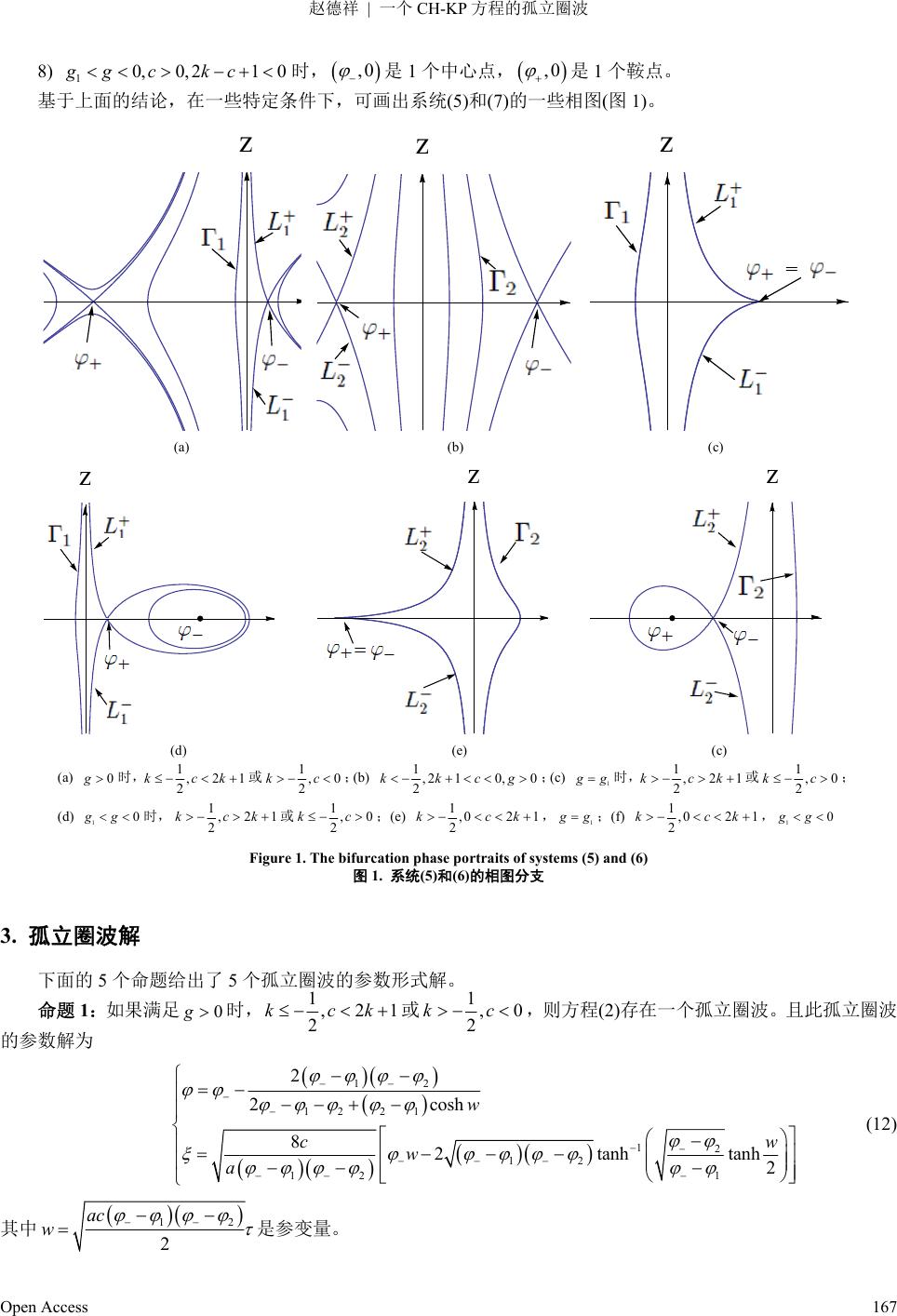 赵德祥 一个 CH-KP 方程的孤立圈波 8) 时, 是1个中心点, 10,0,21 0gg ckc ,0 ,0 是1个鞍点。 基于上面的结论,在一些特定条件下,可画出系统(5)和(7)的一些相图(图1)。 z z z (a) (b) (c) z z z (d) (e) (c) (a) 时, 0g1,21 2 kck或1,0 2 kc ;(b) 1,2 10,0 2 kkcg ;(c) 1 g g 时, 1,2 2 kck 1 或1, 2 kc 0 ; (d) 时, 1 gg01,21 2 kck 或1,0 2 kc ;(e) 1,02 1 2 kck ,1 g g ;(f) 1,02 1 2 kck , 10gg Figure 1. The bifurcation phase portraits of systems (5) and (6) 图1. 系统 (5)和(6)的相图分支 3. 孤立圈波解 下面的 5个命题给出了5个孤立圈波的参数形式解。 命题 1:如果满足 时, 0g1,2 2 kck 1 或1, 2 kc 0 ,则方程(2)存在一个孤立圈波。且此孤立圈波 的参数解为 12 12 21 12 12 12 1 2 2cosh 82tanh 2 w cw w a tanh (12) 其中 1 2 ac w 2 是参变量。 Open Access 167  赵德祥 一个 CH-KP 方程的孤立圈波 命题 2:如果 1,2 10,0 2 kkcg ,则方程(2)存在一个孤立圈波。且此孤立圈波的参数解为 12 12 21 11 12 12 2 2 2cosh 82tanhtanh 2 w cw w a (13) 其中 12 2 ac w 参变量。 命题 3:如果满足 1 g g时, 1,0,2 2 kcck 1 或1, 2 kc0 ;记 021kc a ,则方程(2)存在一个 孤立圈波。且此孤立圈波的参数解为 01 022 01 01 0 4 4 82arctan 2 w cww a (14) 其中 2 ac w 是参变量。 命题 4:如果满足 时, 10gg 1,2 2 kck 1 或1, 2 kc0 ,则方程(2)存在一个孤立圈波。且此孤立 圈波的参数解为 12 12 21 1 12 12 2 2 2cosh 82arctan 2 w cw w a tanh (15) 其中 12 2 ac w 是参变量。 命题 5:如果 1,02 1 2 kc k ,10gg ,则方程(2)存在一个孤立圈波。且此孤立圈波的参数解为 12 12 21 1 12 12 2 2 2cosh 82arctan 2 w cw w atanh (16) 其中 12 2 ac w 是参变量。 证明:只证命题1和命题 2,其余3个命题有类似的证明。 命题 1的证明,如果满足时, 0g1,2 2 kck 1 或1, 2 kc 0 ,则过 ,0 的异宿轨线 1 L 、1 L 和开 轨线 等势,且在渐近线两侧(看图 1(a)),所以方程(2)有一个孤立圈波。根据(8)式, 1 1 L 、1 L 和由方程 所确定。于是 1 Hz ,H ,0 2 12 2 42 a zc (17) 其中 12 。 Open Access 168  赵德祥 一个 CH-KP 方程的孤立圈波 把(17)代入系统(7 ) 的第一个方程,沿 1 L 、1 L 和1 积分,得 12 12 21 2 2cw osh (18) 其中 1 2 ac w 2 是参变量。 把(18)代入系统(6 ) 积分,得 12 12 12 1 82tanh 2 cw w a tanh (19) 结合(18)和(19),即得孤立圈波解(12)。 命题 2的证明,在满足 1,210,0 2 kkcg 时,过 ,0 的异宿轨线 2 L 、2 L 和开轨线 等势,且在 2 渐近线两侧(看图1(b)),所以方程(2)有一个孤立圈波。根据(8)式,2 L 、2 L 和2 由方程 所确 定。于是 ,,HzH 0 2 12 2 42 a zc (20) 其中 12 。 把(20)代入系统(7 ) 的第一个方程,沿 2 L 、2 L 和2 积分,得 12 12 21 2 2cw osh (21) 其中 12 2 ac w 是参变量。 把(21)代入系统(6 ) 积分,得 11 12 12 2 82tanhtanh 2 cw w a (22) 结合(21)和(22),即得孤立圈波解(13)。 依据(12)和(13),用 Mathematica 7.0可画出两个孤立圈波的平面图图2。 10 6 2 2610 1 1 3 u 10 6 22610 3 1 1 u (a) (b) Figure 2. The solit ary l o o p waves of Equation (2) with 1, 1ak and 6g ; (a) ; (b) 1.5c 0.5c 图2. ,时,方程(2)的孤立圈波平面模拟图;(a) 1, 1ak 6g1.5c ;(b) 0.5c 4. 结论 在的条件下,本文用微分方程动力系统方法研究一个 CH-KP 方程。找到了孤立圈波的存在条件。计0a Open Access 169  赵德祥 一个 CH-KP 方程的孤立圈波 Open Access 170 算出了孤立圈波的精确参数函数表达式。用 Mathematica 7.0模拟出了两个孤立圈波的平面图(看图2),这 些 结 果 丰富了 CH-KP 方程的研究内容。 5. 致谢 感谢谢绍龙教授在本文写作中所提的宝贵意见。 参考文献 (References) [1] Zhang, K.L., Tang, S.Q. and Wang, Z.J. (2010) Bifurcation of travelling wave solutions for the generalized Camassa-Holm-KP equations. Communications in No nlinear Science and N umerical Simulation, 15, 564-572. [2] Biswas, A. (2009) 1-Soliton solution of the generalized Camassa-Holm Kadomtsev-Petviashvili equation. Communications in Nonlinear Sci- ence and Numerical Simulation, 14, 2524-2527. [3] 谢绍龙, 洪晓春 (2009) Reduced Ostrovsky方程的周期圈波解. 湖南师范大学自然科学学报 , 32, 3-16. [4] Xie, S.L. and Wang, L. (2010) Compacton and generalized kink wave solutions of the CH-DP equation. Applied Mathematics and Computa- tion, 215, 4028-40 39. |