多元插值格式的计算机实现 Acquired by Computer on the Schemes of Multivariate Interpolation

doi:10.12677/AAM.2013.24024

设为首页加入收藏期刊导航网站地图

期刊菜单

文章导航

Advances in Applied Mathematics 应用数学进展, 2013, 2, 179-185

http://dx.doi.org/10.12677/aam.2013.24024 Published Online November 2013 (http://www.hanspub.org/journal/aam.html)

Acquired by Computer on the Schemes of Multivariate

Interpolation*

Lihong Cui1, Xiaowan Wang1, Yinong Yang1, Huan Bao2

1College of Mathematics, Liaoning Normal University, Dalian

2College of Mathematics, Dalian University of Technology, Dalian

Email: cuilihong@lnnu.edu.cn, 377057874@qq.com, fytjmflvv907@qq.com, 12190499882@qq.com

Received: Oct. 30th, 2013; revised: Nov. 12th, 2013; accepted: Nov. 18th, 2013

permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract: Multivariate interpolation is one of the hot research problems of computational mathematics, which

derives its widespread application in the list, the multiple functions of finite element method, industrial prod-

uct design, research and production. This paper first introduces the basic concepts of multivariate interpola-

tion, and then studies the existence and uniqueness of multivariate interpolation function, that is, how to cho-

ose the set of nodes to make the existence and uniqueness of multivariate interpolation polynomial function at

the same time; this paper gives some construction methods on set of nodes for multivariate interpolation, such

as: linear superposition method and curve superposition method. The application of construction method is

given in this paper. We use MATLAB software to realize binary linear interpolation, binary quadric and bi-

nary cubic interpolation and find that interpolation effect is also getting better and better along with the in-

crease in the degree of interpolation polynomial

Keywords: Well-Posed Node Set; The Multivariate Polynomial; The Multivariate Interpolation

多元插值格式的计算机实现*

崔利宏 1，王晓婉1，杨一浓 1，鲍焕2

1辽宁师范大学数学学院，大连

2大连理工大学数学学院，大连

Email: cuilihong@lnnu.edu.cn, 377057874@qq.com, fytjmflvv907@qq.com, 12190499882@qq.com

收稿日期：2013 年10 月30 日；修回日期：2013 年11 月12 日；录用日期：2013 年11 月18日

摘要：多元插值是目前计算数学领域的一个热门研究问题，这源于它在多元函数列表、有限元法、

工业产品外形设计等实际科研生产中的广泛应用。本文首先介绍了多元插值的基本概念，进而研究了

多元插值函数的存在唯一性问题，也就是如何选择结点组才能使多元插值多项式函数惟一存在问题，

同时本文给出了多元插值结点组的一些构造方法，如：直线法叠加法、弧线叠加法。本文将这两种构

造方法应用到具体的示例中，最后应用本文给出的构造方法，我们用 MATLAB 软件来分别实现了二

元一次、二元二次和二元三次插值，并将它们进行了对比，发现随着插值多项式次数的增加插值效果

也越来越好。

关键词：适定结点组；多元多项式；多元插值

*基金项目：本论文得到国家自然科学基金(NO：41171137)项目资助。

Open Access 179

崔利宏等  多元插值格式的计算机实现

1. 引言

多元插值问题是计算数学领域中一个非常重要的基本问题，同时也是一个经典的数学问题，在计算数学中

占据着核心地位。由于多元插值在许多科研领域有广泛的应用，因此多元插值问题的研究也越来越受到人们的

重视。但是，传统的多元差值格式的构造方法，其中的公式十分繁琐，计算量又很大，单纯依赖便携式计算器

或手工操作是远远达不到科研生产需要的，因此如果能够使用计算机来解决插值问题的一个很重要的手段，本

文就是利用MATLAB 数学软件来实现多元插值。

本文参考[1,2]中给出了多元插值问题的定义，提出了文章研究的课题；参考文献[3,4]给出的适定结点组存在性

和唯一性的相关定理，并给出了选取适定结点组的几种方法，为下文具体示例中选取适定结点组用MATLAB

软件来实现插值做理论铺垫；借鉴文献[5,6]，本文选择适当示例用MATLAB 软件[7]编程得以实现多元插值格式，

并给出了相应插值多项式及被插函数的图像，以便直观地观察插值的效果。

1.1. 多元多项式函数插值问题提法

定义 1[1]：设，，…，



1,Pxy



2,Pxy







Pxy

是一组线性无关的实系数二元多项式

















Span,, ,,, ,

PPxyPxyPxy，

D是上的有界闭区域，



D，是 D中互异的点。二元多项式插值问题，寻找 p P，使得下

述插值条件被满足：

1,,

qq









,1,,

pqf qik (1)

这样的多项式称为



,pxy







xy在P中的插值多项式，称为插值结点。

1,,

qq

1.2. 多元插值多项式存在性讨论

定义 1[3]：(Haar 定理)设S是欧式空间





Rn中包含一个内点 q的点集。设定义于 S

上，且其中每个函数均在 q的一个邻域内连续，则这个函数组在 S上不是唯一可解的。



,,, 1

 





根据 Haar定理，在构造多元插值多项式时，插值结点组的选取是一个关键的问题，因为并不是对于任意给

定的插值结点组，多元插值多项式都是存在并且唯一的，为求得插值多项式，首要的问题就是选择插值结点组

，使得插值问题(1)的解存在并且唯一。

1,,

qq

定义 2：若对任意给定的被插函数



xy，插值问题 (1 )的解均存在并且唯一，则称是空间的适

定结点组。

1,,

qqP

引理 1[2]：点组是空间P的适定结点组，必须且只须该点组不在P中的任何一条代数曲线上。

1,,

qq

2. 主要定理及其证明

关于的适定结点组的选取问题本文给出下列构造方法。

定理 2：(多元插值函数适定结点组构造方法)若是的适定结点组，且它们的每个点都不在某条

次(或2)不可约代数曲线

1,,

qqn

1l





,qxy0

上。则将在该曲线上任取的





3nl1



个不同点与放在一起，必

构成空间的一个适定结点组。

1,,

qq

P

证明：用A表示不可约代数曲线



,qxy 0



上所取的





3nl1



个不同点的集合，



的点数

q



。

用B表示这两个点集的并，则点集 B的点数恰与 nl



的维数 2

2nl



相同(注： 1l



或2)。利用反证法来证明B是

的适定结点组。假若B不是 P适定结点组，则由引理，必存在非零多项式

Pnl的





y P



,xp 得B中的所有

点落在代数曲线



p。但 A中的点均位于不可约代数曲线

使

0上,xy





,0qxy



上，于是 l次不可约代数曲线





,y0qx 与代数曲线至少有



,y0px





1l31nl n个交点。由Bezout定理，与必有公



,pxy



,yqx

Open Access 180

崔利宏等  多元插值格式的计算机实现

因子存在。但是不可约多项式，是故



,qxy







,qxy必为





,pxy的因子。即有多项式因子存在，使

得



rxy P

 

pxy xy



,,qxyr ,





,1,

i2,

rqpq qq,k注意到





是的适定结点组，所以



,0yrx



，

进而，此与是非零多项式的假设相矛盾。



,pxypx0





3. 适定结点组的构造方法

利用定理 2可以构造出一系列的适定结点组，例如有以下构造的适定结点组的几个方法：

3.1. 直线型结点组

第0步：在上任取一点作为结点，

第1 步：在上任做一条直线1不通过点 1，在其上任取两个互不相同的点作为新增加的结点，

Rl Q

…………………，

第n步：在上任做一条直线不同过前面已经选好的点，在其上任取 n + 1个互不相同的点作为新增加

的结点，

当n步完成时所得到的结点组记为，并称它为直线型结点组。根据定理 2显然是的适定结点组(例

如图 1的取法)。

Q4 Q5 Q6

Q2 Q3

Figure 1. Method of adding the straight-lines

图1. 添加直线法

3.2. 弧线型结点组

第0步：在上任取一点作为结点，

第1步：在上任做一条二次不可约曲线 (可以是椭圆、双曲线或抛物线)不通过点，在其上任选 5个

互不相同的点作为新增加的结点，

………………，

第n步：在上再做一条二次不可约曲线不通过前面已经选好的点，在其上任选4n + 1 个互不相同的点

作为新增加的结点，

当n步完成时所得到的结点组记为 2n

，称为2n次弧线型结点组(例如图2的取法)。

Figure 2. Method of adding the conic curves

图2. 添加圆锥曲线法

Open Access 181

崔利宏等  多元插值格式的计算机实现

定理 3：2n

是的适定结点组。

然，

证明：显2n

是P的插值结点组。下面只需要证 2n

2n的适定性。用数学归纳法。当 n = 0时命题显然

为真。现在假设命题nk真，来证对 1nk也为真。用法，假若不然，则根据引理 2，H必在 P

对为反证



21k



21k



中的某条代数曲线



 



00 1001210

02 1

Pxyccxcycx



 

 



设的方程是：

由于它是一条二次曲线，故其二次项系数不全为0，并且如果它不是

l



00 1001112002

,0Qxyxy xyxy

 

 





,0Pxy



的分量，则根据Bezout 定

理，它至多和



,Pxy交于





41k个点，但是按照我们的选点规则， 1k



包含





41k



个中的点，也就是

说，它与





41k



21k

H



,0y有



个交点，这就发生了矛盾。因此 1k



一定是





,0Pxy



的分量，从而有分解式：













,,xyPx,Pxy y



y是2k次多项式。由选点规则知，

Q其中 1,Px 1k



不通过第 k + 1步以前所选取的点，

组因此 1



y,0通过结点 2k

，由引理 2，此处的 2n

在中不适定，，该命题得证。

点O为圆心做 n个不同的同心圆周，周上分别取 5, 9,13,,41n个不同的点，则

P矛盾。故此

推论 1：以一在每个圆这

些点和一般地

点O就作定了 P中的一个适定结点组。另外添加直线法和添加弧线法可，若已知的

一个适定结点组，则在不通过的任何一条 i次(i = 1或2)曲线上再取

2n交替使用。 n





21n



个点，便可构成的适定结

点组。

1：

P

T

注记以上给出的构造多元函数插值适定结点组的方法是与要插值的函数无关的；也就是说只要在实际

科研生产

多元多项式插值示例

例1：用多项式插值

中给定了要插值的函数，按照我们给出的构造插值结点组的方法，就一定能够构造出唯一的插值多项

式来，通常，只要插值的函数不同，所构造出的插值多项式函数也会不同。



xyx y这个二元函数。我们先用二元一次多项式函数做插值函数：取点



10, 0Q作为结点，作直线 1





适定

如图 2~4 所示，并在该直线上取异于点的两点



，



作为结点，

知，，为一组结点组，一次插值多项式为：

Q20,1Q31, 0Q

由定理 31





xyx y



。

-2



= -x+1Q2

Figure 3. A diagrammatic sketch of example one (interpolation of degree one)

用二元二次多项式函数做插值函数：

图3. 例一的示意图(一次插值)

取点





，





40, 1Q







20,1Q，





31, 0Q，，和



51, 0Q

10, 0Q作为结点，做单位圆，在单位圆取

Q





这5个互异的点作为结点组(如图 4所示)，由定理 3可知，所取点组为适定结点组，

,,QQ

Open Access 182

崔利宏等  多元插值格式的计算机实现

得到该函数的二次插值多项式为：



2,22

xyx y。

-2

Figure 4. example one (interpolation of degre e two)

图(二次插值)

用二元三次多项式函

在平面直角坐标系中做单位圆并将其记正五边形，延长五边形的五条边，得到这

五条记圆为，则和是同心圆，经计算得圆的半径为

A diagrammatic ketch of

图4. 例一的示意

数做插值函数：

为O，并做该单位圆的内接

该边分别相交于五个点且这五个点共圆， 21 22

OO OO35

如图 5所示，在圆 1

O上取互异的 5个点

，

Q



，











0, 2

Q



，





3,0

Q









，40,

Q











，

32 1032 10

Q





，在圆 2

O上取个点



互异的 5





61,0Q，





0,1Q7，



81,0Q9

Q





，，

Q





，由定理2.3得，得

110

,,QQ是一个适定结点组到





0 .4472

30.44,.552872 0

xyx y

数的二次插值

 ，即为该函

多项式。

-2

Q8 Q6

Q10

Figure 5. A diagrammatic sketch of example one (interpolation of degree three)

图5. 例一的示意图(三次插值)

. 用MATLAB 来实现多项式插值 5

),( xyxf 给定要插值的函数： y，用MATLAB 软件实现二元一次、二元二次和二元三次插值图

像如下：

Open Access 183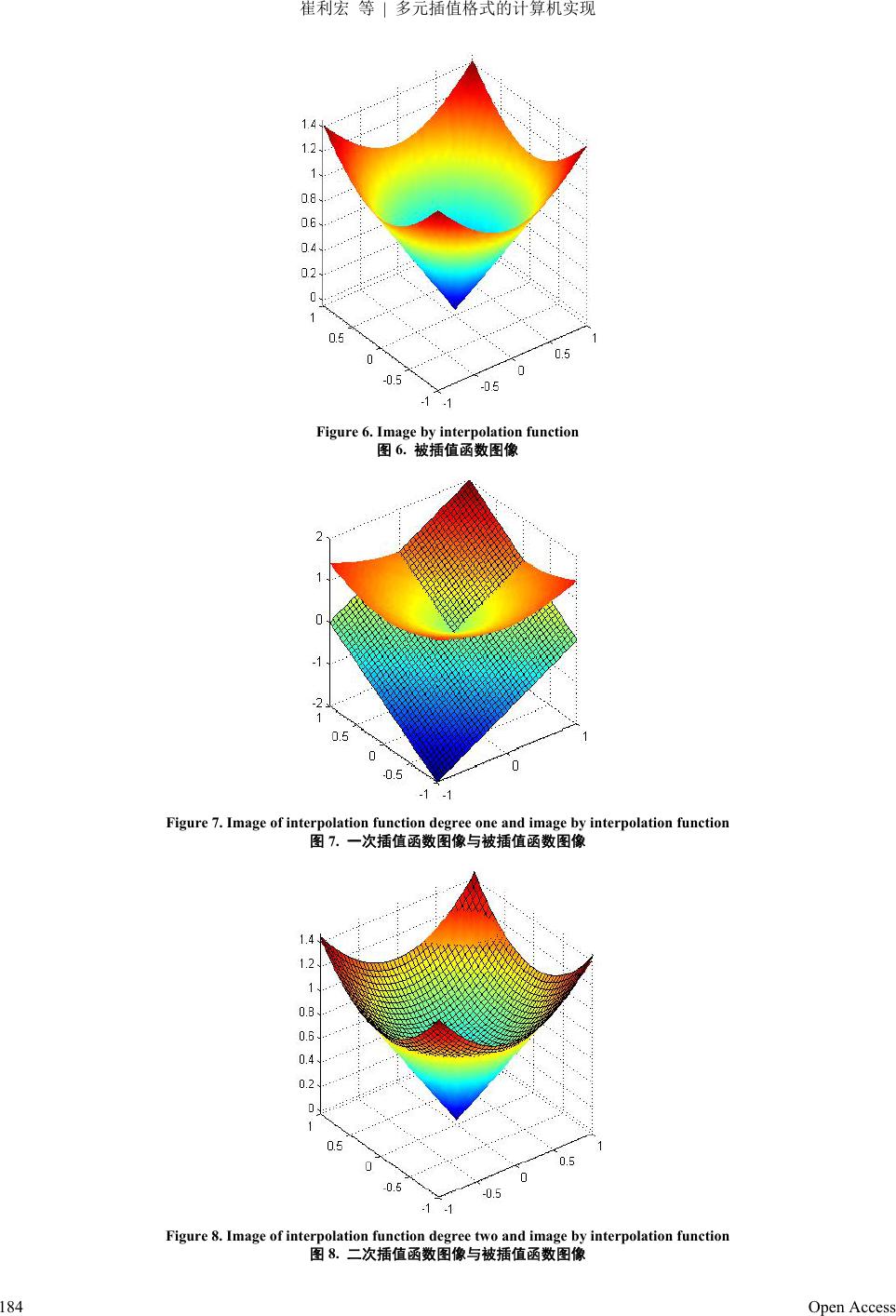

崔利宏等  多元插值格式的计算机实现

Figure 6. Image by interpolation function

图6. 被插值函数图像

Figure 7. Image of interpolation function degree one and image by interpolat i on function

图7. 一次插值函数图像与被插值函数图像

Figure 8. Image of interpolation function degree two and image by interpolation function

图8. 二次插值函数图像与被插值函数图像

Open Access 184

崔利宏等  多元插值格式的计算机实现

Open Access 185

说明：图 6是插值函数

igure 9. Image of interpolation function degree three and image by interpolation function

图9. 三次插值函数图像与被插值函数图像



xyx y的曲面图；图 7是构造出的二元一次插值函数插值效果图；图 8

是构造出的二元二次插值函数插值效果图；图 9是构造出的二元三次插值函数插值效果图。

由以上图像我们可以看出：随着插值次数的增加插值效果越来越好，插值多项式的图像越来越贴近原函数

图像。

比如，我们用插值多项式求在





1, 1 处的函数值，一次、二次、三次的插值结果分别为：−2.00，2.00，1.4472，

而在该点处的精确值为 2，那么误差分别为 122 3.414t ，222 0.586t ，31.44722 0.033t。

6. 致谢

本文得到国家自然科学基金(NO：41171137)项目资助；感谢吉林大学数学科学学院梁学章教授的悉心指导。

参考文献 (References)

] 王仁宏 (2005) 数值逼近. 高等教育出版社

[2] . 国防工业出版社, 北

[5]

峰 (2010) MATLAB数值分析第二版. 机械工业出版社, 北京.

[7] 与应用

[1 , 北京.

梁学章, 李强 (2005) 多元逼近京.

[3] Kincaid D. and Cheney W. 著, 王国荣, 余耀明, 徐兆亮, 译 (2005) 数值分析. 机械工业出版社, 北京.

[4] 崔利宏, 姜志敏 (2008) 关于多元分次插值结点组适定性问题的研究.

延边大学学报

(

自然科学版

), 2, 86-88.

梁学章 (1979) 二元插值的适定结点组与迭加插值法.

吉林大学自然科学学报

, 1, 27-32.

[6] 张德

张德峰, 著 (2007) MATLAB数值分析 . 国防工业出版社, 北京.