ABSTRACT

Combing A. Genocchi’s definition of the Genocchi numbers in 1852, L. Carlitz’s definition of the degenerate Bernoulli numbers in 1956, M. Kaneko’s definition of poly-Bernoulli numbers in 1999 and T. Kim et al.’s definition of fully degenerate poly-Bernoulli polynomials in 2016, in this paper, we introduce the notion of the fully degenerate poly-Genocchi polynomials, we also investigate their properties and prove five combinatorial identities of them.

Keywords:Genocchi Polynomial, The Fully Degenerate Poly-Genocchi Polynomials

完全退化的Poly-Genocchi多项式

秦松

华南理工大学数学学院，广东 广州

收稿日期：2020年3月27日；录用日期：2020年4月16日；发布日期：2020年4月23日

摘 要

结合意大利学者A. Genocchi于1852年关于经典Genocchi数的定义，美国学者L. Carlitz于1956年关于退化Bernoulli数的定义，日本学者M. Kaneko于1999年关于poly-Bernolli数的定义，以及韩国学者T. Kim等人于2016年关于完全退化的poly-Bernoulli多项式的定义，本文给出了完全退化的poly-Genocchi多项式的定义，研究了它们的性质，并得到了关于它们的五个组合恒等式。

关键词 :Genocchi多项式，完全退化的Poly-Genocchi多项式

Copyright © 2020 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

1713年，瑞士数学家Jocob Bernoulli引进了Bernoulli数的概念，用以解决Leibniz关于自然数的幂和问题 [1]。他证明了

$1^n+2^n+3^n+\cdot \cdot \cdot +m^n=\frac{B_{n+1}\left(m+1\right)-B_{n+1}}{n+1}\mathrm{.}$

这里Bernoulli多项式 $B_n\left(x\right)$ 由生成函数

$\frac{t{\text{e}}^{xt}}{{\text{e}}^t-1}={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}}{B}_n\left(x\right)\frac{t^n}{n!}$

所定义，而数 $B_n=B_n\left(0\right)$ 称为Bernoulli数(见文献 [1] 定理2)。1874年，德国数论学家E. Kummer利用Bernoulli数给出了非正则素数的定义，并用以解决代数数论中关于分圆域的类数和素数幂次Fermat方程的解的问题(见文献 [2])。

1755年，L. Euler为计算交错幂和引入了Euler多项式的定义。他证明了

$1^n-2^n+3^n+\cdot \cdot \cdot +{\left(-1\right)}^{\left(m+1\right)}{m}^n=\frac{{\left(-1\right)}^m{E}_n\left(m+1\right)+E_n\left(0\right)}{2}\mathrm{.}$

这里Euler多项式 $E_n\left(x\right)$ 由生成函数

$\frac{2{\text{e}}^t}{{\text{e}}^t+1}{\text{e}}^{xt}={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}}{E}_n\left(x\right)\frac{t^n}{n!}$

所定义(见文献 [1] 定理2)。1852年，德国数学家Scherk在著作中首次明确了Euler数和Euler多项式

的称谓 [3]。按照他的叫法，故 $E_k=2^k{E}_k\left(\frac{1}{2}\right),\mathrm{<mi>\; </mi>}k=0,1,2,\cdot \cdot \cdot$ 被称为Euler数。

1852年，为了研究对称群 $S_{2n-1}$ 中置换的组合性质，意大利数学家Angelo Genocchi给出了Genocchi数 $G_n$ 的定义：

$\frac{2t}{{\text{e}}^t+1}{\text{e}}^{xt}={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}}{G}_n\left(x\right)\frac{t^n}{n!}.$

而k阶Genocchi多项式 $G_n^{\left(k\right)}\left(x\right)$ 定义为：

${\left(\frac{2t}{{\text{e}}^t+1}\right)}^k{\text{e}}^{xt}={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}}{G}_n^{\left(k\right)}\left(x\right)\frac{t^n}{n!},$ (1)

当 $x=0$ 时， $G_n^{\left(k\right)}=G_n^{\left(k\right)}\left(0\right)$ 为k阶Genocchi数，当 $k=1$ 时， $G_n^{\left(1\right)}\left(x\right)=G_n\left(x\right)$ 为Genocchi多项式 [4]。

2019年，类比Kummer在1874年的工作，胡甦老师，Min-Soo Kim，沙敏老师以及德国学者Pieter Moree在文 [5] 中给出了Genocchi数对应的非正则多项式的定义，并得到了它们与分圆域类数之间的联系。

从数学分析我们知道

$e=\underset{n\to \infty }{lim}{\left(1+\frac{1}{n}\right)}^n\mathrm{,}$

(见文献 [6] 的第74页)。类比Bernoulli数的定义，美国著名数论学家L. Carlitz [7] 在1956年提出退化的Bernoulli数的定义：

$\frac{t}{e_{\lambda }\left(t\right)-1}=\frac{t}{{\left(1+\lambda t\right)}^{\frac{1}{\lambda }}-1}{\left(1+\lambda t\right)}^{\frac{x}{\lambda }}={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}}{\beta }_{n,\lambda }\frac{t^n}{n!},$ (2)

并得到了相应的Staudt-Clausen定理，见文献 [8]。

1999年，日本数论学家Arakawa和Kaneko [9] 通过Mellin变换给出了一类新的zeta函数 ${\zeta }_k\left(s\mathrm{,}x\right)$ 的定义：

$\Gamma \left(s\right){\zeta }_k\left(s,x\right)={\displaystyle {\int }_0^{\infty }}{t}^{s-1}\frac{L{i}_k\left(1-{\text{e}}^{-t}\right)}{1-{\text{e}}^{-t}}{\text{e}}^{-xt}\text{d}t,$

其中 $L{i}_k\left(z\right)={\displaystyle {\sum }_{m=1}^{\infty }}\frac{z^m}{m^k}$ 为k阶超对数(polylogarithm)函数。他们发现上面所定义的zeta函数 ${\zeta }_k\left(s\mathrm{,}x\right)$ 在负整

数处的特殊值通过poly-Bernoulli多项式加以表达，即

${\zeta }_k\left(-n\mathrm{,}x\right)={\left(-1\right)}^n{B}_n^{\left(k\right)}\left(x\right)\mathrm{.}$

这里poly-Bernoulli多项式定义为：

$\frac{L{i}_k\left(1-{\text{e}}^{-t}\right)}{1-{\text{e}}^{-t}}{\text{e}}^{xt}={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}}{B}_n^{\left(k\right)}\left(x\right)\frac{t^n}{n!},$ (3)

并且 $B_n^{\left(k\right)}=B_n^{\left(k\right)}\left(0\right)$ 称为poly-Bernoulli数。

2015年，韩国特殊函数方向的专家T. Kim研究了一类退化的zeta函数并发现它在复平面上是解析的，并且在负整数处的特殊值即为Carlitz的退化Euler多项式 [10]。随后，他又在2016年推导出退化q-Bernoulli多项式的系列性质 [11] [12]。与此同时，他与俄罗斯学者D. V. Dolgy合作，用p-进~q-积分得出了退化q-Euler多项式的对称性 [13]。之后，他与D. S. Kim等学者合作对退化的Frobenius-Euler数和退化的poly-Bernoulli数，poly-Bernoulli多项式进行了研究，将若干经典的性质推广到了退化情形 [14] [15]。另外，他们还给出了完全退化的poly-Bernoulli多项式的定义：

$\frac{L{i}_k\left(1-{\left(1+\lambda t\right)}^{-\frac{1}{\lambda }}\right)}{1-{\left(1+\lambda t\right)}^{-\frac{1}{\lambda }}}{\left(1+\lambda t\right)}^{\frac{x}{\lambda }}={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}}{\beta }_{n,\lambda }^{\left(k\right)}\left(x\right)\frac{t^n}{n!},$ (4)

并对其性质进行了详细证明 [16]。

受经典Genocchi多项式的定义(1)，退化的Bernoulli数的定义(2)，poly-Bernoulli多项式的定义(3)以及完全退化的poly-Bernoulli多项式的定义(4)的启发，我们通过下面的生成函数给出退化的Genocchi多项式 ${\mathcal{G}}_{n\mathrm{,}\lambda }\left(x\right)$ 的定义：

$\frac{2t}{{\left(1+\lambda t\right)}^{\frac{1}{\lambda }}+1}{\left(1+\lambda t\right)}^{\frac{x}{\lambda }}={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}}{\mathcal{G}}_{n,\lambda }\left(x\right)\frac{t^n}{n!},$ (5)

当 $x=0$ 时， ${\mathcal{G}}_{n\mathrm{,}\lambda }\left(0\right)={\mathcal{G}}_{n\mathrm{,}\lambda }$ 被称为退化的Genocchi数。注意到，

$\frac{2t}{{\text{e}}^t+1}{\text{e}}^{xt}=\underset{\lambda \to 0}{\lim }\frac{2t}{{\left(1+\lambda t\right)}^{\frac{1}{\lambda }}+1}{\left(1+\lambda t\right)}^{\frac{x}{\lambda }}={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}}\underset{\lambda \to 0}{\lim }{\mathcal{G}}_{n,\lambda }\left(x\right)\frac{t^n}{n!},$

故 $G_n\left(x\right)=li{m}_{\lambda \to 0}{\mathcal{G}}_{n\mathrm{,}\lambda }\left(x\right)$。我们也通过下面的生成函数给出poly-Genocchi多项式的定义：

$\frac{L{i}_k\left(1+{\text{e}}^t\right)}{1+{\text{e}}^t}{\text{e}}^{xt}={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}}{G}_n^{\left(k\right)}\left(x\right)\frac{t^n}{n!},$ (6)

当 $x=0$ 时， $G_n^{\left(k\right)}=G_n^{\left(k\right)}\left(0\right)$ 是poly-Genocchi数。当 $k=1$ 时，有 $G_n^{\left(1\right)}\left(x\right)=\frac{1}{2}{G}_n\left(x\right)$，这是因为

${\displaystyle \underset{n=0}{\overset{\infty }{\sum }}}{G}_n^{\left(1\right)}\left(x\right)\frac{t^n}{n!}=\frac{t}{1+{\text{e}}^t}{\text{e}}^{xt}=\frac{1}{2}{\displaystyle \underset{n=0}{\overset{\infty }{\sum }}}{G}_n\left(x\right)\frac{t^n}{n!}.$

我们还通过下面的生成函数给出完全退化的poly-Genocchi多项式的定义：

$\frac{L{i}_k\left(1+{\left(1+\lambda t\right)}^{\frac{1}{\lambda }}\right)}{1+{\left(1+\lambda t\right)}^{\frac{1}{\lambda }}}{\left(1+\lambda t\right)}^{\frac{x}{\lambda }}={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}}{\mathcal{G}}_{n,\lambda }^{\left(k\right)}\left(x\right)\frac{t^n}{n!},$ (7)

当 $x=0$ 时， ${\mathcal{G}}_{n\mathrm{,}\lambda }^{\left(k\right)}={\mathcal{G}}_{n\mathrm{,}\lambda }^{\left(k\right)}\left(0\right)$ 被称为完全退化的poly-Genocchi数。注意到，

$\frac{2t}{{\text{e}}^t+1}{\text{e}}^{xt}=\underset{\lambda \to 0}{\lim }\frac{2t}{{\left(1+\lambda t\right)}^{\frac{1}{\lambda }}+1}{\left(1+\lambda t\right)}^{\frac{x}{\lambda }}={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}}\underset{\lambda \to 0}{\lim }{\mathcal{G}}_{n,\lambda }\left(x\right)\frac{t^n}{n!},$

故 $G_n^{\left(k\right)}\left(x\right)=li{m}_{\lambda \to 0}{\mathcal{G}}_{n\mathrm{,}\lambda }^{\left(k\right)}\left(x\right)$。

本文沿着前人的道路研究了上面定义的完全退化的poly-Genocchi多项式 ${\mathcal{G}}_{n\mathrm{,}\lambda }^{\left(k\right)}\left(x\right)$ 的性质，并得到了

关于它们的下面五个组合恒等式。

定理1 下面等式成立：

${\mathcal{G}}_{n\mathrm{,}\lambda }^{\left(k\right)}\left(x+y\right)={\displaystyle \underset{l=0}{\overset{n}{\sum }}}\left(\begin{array}{c}n\\ l\end{array}\right){\left(\frac{y}{\lambda }\right)}_{n-l}{\lambda }^{n-l}{\mathcal{G}}_{n\mathrm{,}\lambda }^{\left(k\right)}\left(x\right)\mathrm{,\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\left(n\ge \mathrm{0,\; <mi>\; </mi>}k\in \mathbb{Z}\right)\mathrm{.}$

特别地，

${\mathcal{G}}_{n\mathrm{,}\lambda }^{\left(k\right)}\left(x\right)={\displaystyle \underset{l=0}{\overset{n}{\sum }}}\left(\begin{array}{c}n\\ l\end{array}\right){\left(\frac{x}{\lambda }\right)}_{n-l}{\lambda }^{n-l}{\mathcal{G}}_{n\mathrm{,}\lambda }^{\left(k\right)}\mathrm{,\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\left(n\ge \mathrm{0,\; <mi>\; </mi>}k\in \mathbb{Z}\right)\mathrm{.}$

定理2 记 ${\left(j\mathrm{<mo>\; |\; </mo>}\lambda \right)}_n=j\left(j-\lambda \right)\left(j-2\lambda \right)\cdot \cdot \cdot \left(j-\left(n-1\right)\lambda \right)$，有

${\mathcal{G}}_{n,\lambda }^{\left(k\right)}+{\mathcal{G}}_{n,\lambda }^{\left(k\right)}\left(1\right)={\displaystyle \underset{m=0}{\overset{\infty }{\sum }}}{\displaystyle \underset{j=0}{\overset{m+1}{\sum }}}\left(\begin{array}{c}m+1\\ j\end{array}\right)\frac{{\left(j|\lambda \right)}_n}{{\left(m+1\right)}^k},\mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\left(n\ge 0,k\in \mathbb{Z}\right).$

定理3 记 ${\left(j\mathrm{<mo>\; |\; </mo>}\lambda \right)}_n=j\left(j-\lambda \right)\left(j-2\lambda \right)\cdot \cdot \cdot \left(j-\left(n-1\right)\lambda \right)$，有

${\mathcal{G}}_{n\mathrm{,}\lambda }^{\left(k\right)}={\displaystyle \underset{m=0}{\overset{\infty }{\sum }}}{\displaystyle \underset{j=0}{\overset{m}{\sum }}}\left(\begin{array}{c}m\\ j\end{array}\right)\frac{{\left(j|\lambda \right)}_n}{{\left(m+1\right)}^k}\mathrm{,\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\left(n\ge \mathrm{0,\; <mi>\; </mi>}k\in \mathbb{Z}\right)\mathrm{.}$

定理4 记 ${\left(j\mathrm{<mo>\; |\; </mo>}\lambda \right)}_n=j\left(j-\lambda \right)\left(j-2\lambda \right)\cdot \cdot \cdot \left(j-\left(n-1\right)\lambda \right)$，有

${\mathcal{G}}_{n,\lambda }^{\left(k-1\right)}=\left(1+\lambda n\right){\mathcal{G}}_{n,\lambda }^{\left(k\right)}+{\mathcal{G}}_{n+1,\lambda }^{\left(k\right)}+{\displaystyle \underset{m=0}{\overset{n}{\sum }}}\left(\begin{array}{c}n\\ m\end{array}\right){\left(\lambda -1|\lambda \right)}_{n-m}{\mathcal{G}}_{m+1,\lambda }^{\left(k\right)},\mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\left(n\ge 1,\mathrm{<mi>\; </mi>}k\in \mathbb{Z}\right).$

定理5 记 ${\left(j\mathrm{<mo>\; |\; </mo>}\lambda \right)}_n=j\left(j-\lambda \right)\left(j-2\lambda \right)\cdot \cdot \cdot \left(j-\left(n-1\right)\lambda \right)$，有

${\mathcal{G}}_{n,\lambda }^{\left(-k\right)}={\displaystyle \underset{m=0}{\overset{\infty }{\sum }}}{\displaystyle \underset{j=0}{\overset{m}{\sum }}}\left(\begin{array}{c}m\\ j\end{array}\right){\left(j|\lambda \right)}_n{\left(m+1\right)}^k,\mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\left(n\ge 1,\mathrm{<mi>\; </mi>}k\in \mathbb{Z}\right).$

2. 预备知识

2.1. Stirling序列的定义 [5]

第一类Stirling数 $S_1\left(n\mathrm{,}l\right)$ 通过下降阶乘 ${\left(x\right)}_n$ 的展开式中x的幂的系数定义：

${\left(x\right)}_n={\displaystyle \underset{l=0}{\overset{n}{\sum }}}{S}_1\left(n,l\right)x^l,$

第二类Stirling数 $S_2\left(n\mathrm{,}l\right)$ 则被定义为：

$x^n={\displaystyle \underset{l=0}{\overset{n}{\sum }}}{S}_2\left(n,l\right){\left(x\right)}_l.$

这里，当 $n\ge 1$ 时，下降阶乘 ${\left(x\right)}_n=x\left(x-1\right)\left(x-2\right)\cdot \cdot \cdot \left(x-n+1\right)$，${\left(x\right)}_0$ 定义为1。

2.2. 退化的概念 [5]

对 $\lambda \in ℝ\mathrm{,\; <mi>\; </mi>}t\in ℝ$，退化的指数函数 $e_{\lambda }^x\left(t\right)$ 定义为：

$e_{\lambda }^x\left(t\right)={\left(1+\lambda t\right)}^{\frac{x}{\lambda }}={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}}{\left(x\right)}_{n,\lambda }\frac{t^n}{n!},$

其中 ${\left(x\right)}_{n\mathrm{,}\lambda }$ 是退化的下降阶乘，当 $n\ge 1$，${\left(x\right)}_{n,\lambda }=x\left(x-\lambda \right)\left(x-2\lambda \right)\cdot \cdot \cdot \left(x-\left(n-1\right)\lambda \right),\mathrm{<mi>\; </mi>}{\left(x\right)}_{0,\lambda }=1$。

当 $x=1$ 时，

$e_{\lambda }\left(t\right)={\left(1+\lambda t\right)}^{\frac{1}{\lambda }}\mathrm{,}$

注意到， ${\lim }_{\lambda \to 0+}{e}_{\lambda }^x\left(t\right)={\lim }_{\lambda \to 0+}{\left(1+\lambda t\right)}^{\frac{x}{\lambda }}={\displaystyle {\sum }_{n=0}^{\infty }}\frac{{\left(xt\right)}^n}{n!}={\text{e}}^{xt}$。

2.3. 退化的Stirling数，Euler多项式，Bernoulli多项式 [5]

对 $\lambda \in ℝ\mathrm{,\; <mi>\; </mi>}t\in ℝ$，退化的第二类Stirling数 $S_{\mathrm{2,}\lambda }\left(n\mathrm{,}k\right)$ 定义为：

$\frac{1}{k!}\left(e_{\lambda }\left(t\right)-1\right)={\displaystyle \underset{n=k}{\overset{\infty }{\sum }}}{S}_{2,\lambda }\left(n,k\right)\frac{t^n}{n!}.$

注意到， $li{m}_{\lambda \to 0}{S}_{2.\lambda }\left(n\mathrm{,}k\right)=S_2\left(n\mathrm{,}k\right)\mathrm{,}\left(n\mathrm{,}k\ge 0\right)$。

对 $\lambda \in ℝ\mathrm{,\; <mi>\; </mi>}t\in ℝ$，退化的Euler多项式 $E_{n\mathrm{,}\lambda }\left(x\right)$ 由如下的生成函数给出：

$\frac{2}{e_{\lambda }\left(t\right)+11}{e}_{\lambda }^x\left(t\right)=\frac{t}{{\left(1+\lambda t\right)}^{\frac{1}{\lambda }}+1}{\left(1+\lambda t\right)}^{\frac{x}{\lambda }}={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}}{E}_{n\mathrm{,}\lambda }\left(x\right)\frac{t^n}{n\mathrm{<mo>\; !\; </mo>}}\mathrm{,}$

当 $x=0,\mathrm{<mi>\; </mi>}{E}_{n,\lambda }=E_{n,\lambda }\left(0\right)$ 称为退化的Euler数。注意到，

$\frac{2}{{\text{e}}^t+1}{\text{e}}^{xt}=\underset{\lambda \to 0}{\lim }\frac{t}{{\left(1+\lambda t\right)}^{\frac{1}{\lambda }}-1}{\left(1+\lambda t\right)}^{\frac{x}{\lambda }}={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}}\underset{\lambda \to 0}{\lim }{\beta }_{n,\lambda }\left(x\right)\frac{t^n}{n!},$

所以有 $E_n\left(x\right)=li{m}_{\lambda \to 0}{E}_{n\mathrm{,}\lambda }\left(x\right)$。

对 $\lambda \in ℝ\mathrm{,\; <mi>\; </mi>}t\in ℝ$，退化的Bernoulli多项式 ${\beta }_{n\mathrm{,}\lambda }\left(x\right)$ 由如下生成函数给出：

$\frac{t}{e_{\lambda }\left(t\right)-1}{e}_{\lambda }^x\left(t\right)=\frac{t}{{\left(1+\lambda t\right)}^{\frac{1}{\lambda }}-1}{\left(1+\lambda t\right)}^{\frac{x}{\lambda }}={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}}{\beta }_{n,\lambda }\left(x\right)\frac{t^n}{n!},$

当 $x=0,\mathrm{<mi>\; </mi>}{\beta }_{n,\lambda }={\beta }_{n,\lambda }\left(0\right)$ 称为退化的Bernoulli数。注意到，

$\frac{2}{{\text{e}}^t+1}{\text{e}}^{xt}=\underset{\lambda \to 0}{lim}\frac{t}{{\left(1+\lambda t\right)}^{\frac{1}{\lambda }}-1}{\left(1+\lambda t\right)}^{\frac{x}{\lambda }}={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}}\underset{\lambda \to 0}{lim}{\beta }_{n,\lambda }\left(x\right)\frac{t^n}{n!},$

所以有 $B_n\left(x\right)=li{m}_{\lambda \to 0}{\beta }_{n\mathrm{,}\lambda }\left(x\right)$。

2.4. 完全退化的Poly-Bernoulli多项式 [14]

设 $k\in \mathbb{Z}$，完全退化的poly-Bernoulli多项式 ${\beta }_{n\mathrm{,}\lambda }^{\left(k\right)}$ 的生成函数如下：

$\frac{L{i}_k\left(1-{\left(1+\lambda t\right)}^{-\frac{1}{\lambda }}\right)}{1-{\left(1+\lambda t\right)}^{-\frac{1}{\lambda }}}{\left(1+\lambda t\right)}^{\frac{x}{\lambda }}={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}}{\beta }_{n,\lambda }^{\left(k\right)}\left(x\right)\frac{t^n}{n!},$

当 $x=0,\mathrm{<mi>\; </mi>}{\beta }_{n,\lambda }^{\left(k\right)}={\beta }_{n,\lambda }^{\left(k\right)}\left(0\right)$ 称为完全退化的poly-Bernoulli数。注意到，

$\frac{L{i}_k\left(1-{\text{e}}^{-t}\right)}{1-{\text{e}}^{-t}}{\text{e}}^{xt}=\underset{\lambda \to 0}{\lim }\frac{L{i}_k\left(1-{\left(1+\lambda t\right)}^{-\frac{1}{\lambda }}\right)}{1-{\left(1+\lambda t\right)}^{-\frac{1}{\lambda }}}{\left(1+\lambda t\right)}^{\frac{x}{\lambda }}={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}}\underset{\lambda \to 0}{\lim }{\beta }_{n,\lambda }^{\left(k\right)}\left(x\right)\frac{t^n}{n!},$

所以有 $B_n^{\left(k\right)}\left(x\right)=li{m}_{\lambda \to 0}{\beta }_{n\mathrm{,}\lambda }^{\left(k\right)}\left(x\right)$。

3. 关于完全退化的Poly-Genocchi数和多项式的组合恒等式

我们需要下面的引理。

引理 对退化的Genocchi多项式 ${\mathcal{G}}_{n\mathrm{,}\lambda }\left(x\right)$，我们有

(1) ${\displaystyle {\sum }_{n=0}^{\infty }}\left({\mathcal{G}}_{n\mathrm{,}\lambda }\left(1\right)+{\mathcal{G}}_{n\mathrm{,}\lambda }\right)\frac{t^n}{n\mathrm{<mo>\; !\; </mo>}}=2t\mathrm{,\; <mi>\; </mi>}{\mathcal{G}}_{n\mathrm{,}\lambda }\left(1\right)+{\mathcal{G}}_{n\mathrm{,}\lambda }=2{\delta }_{\mathrm{1,}n}\mathrm{<mi>\; </mi>}\left(n\ge 0\right)\mathrm{,\; <mi>\; </mi>}{\mathcal{G}}_{\mathrm{0,}\lambda }=0$，

(2) ${\mathcal{G}}_{n\mathrm{,}\lambda }\left(x\right)={\displaystyle {\sum }_{l=0}^{\infty }}\left(\begin{array}{c}n\\ l\end{array}\right){\mathcal{G}}_{n\mathrm{,}\lambda }{\lambda }^{n-l}{\left(\frac{x}{\lambda }\right)}_{n-l}$。

证明 (1) 根据退化的Genocchi多项式的定义(5)，当x分别取1和0时有

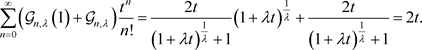
(2) 根据退化的Genocchi多项式的定义(5)有

这里是第一类Stirling数。 □

定理1 下面等式成立：

(8)

特别地，

(9)

定理1的证明 根据完全退化的poly-Genocchi多项式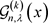的定义(7)有

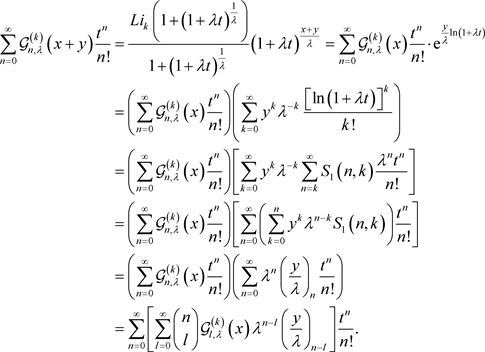
这里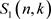是第一类Stirling数，比较上式两端关于项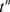的系数，得到

特别地，当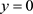时，有

比较上式两端关于项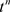的系数即得定理的结论。 □

定理2 记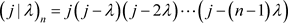，有

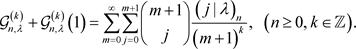(10)

定理2的证明 根据完全退化的poly-Genocchi多项式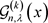的定义(7)有

比较上式两端关于项的系数即得定理的结论。 □

定理3 记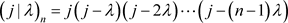，有

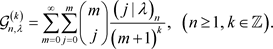(11)

定理3的证明 根据完全退化的poly-Genocchi多项式的定义(7)有

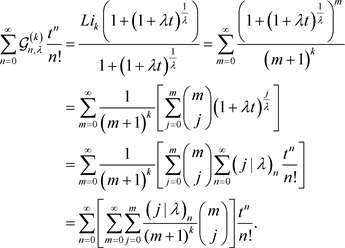
比较上式两端关于项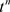的系数即得定理的结论。 □

定理4 记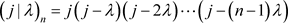，有

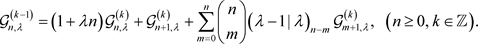(12)

定理4的证明 根据完全退化的poly-Genocchi多项式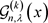的定义(7)有

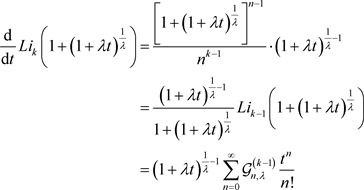(13)

和

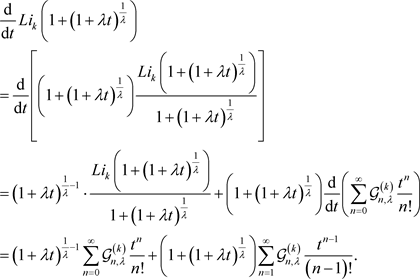(14)

比较等式(13)，(14)得到

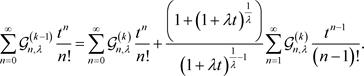
进一步化简得：

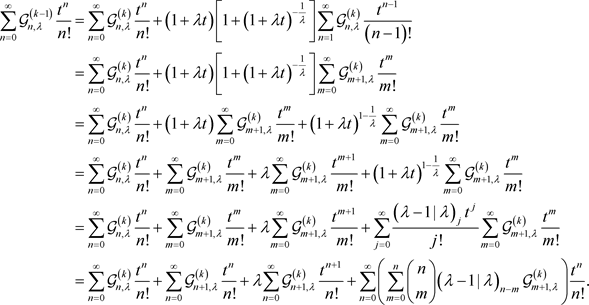
比较上式两端关于项的系数，得到

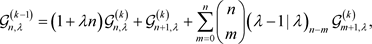
此即得定理的结论。 □

定理5 记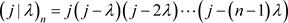，有

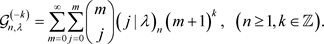(15)

定理5的证明 根据完全退化的poly-Genocchi多项式的定义(7)有

于是

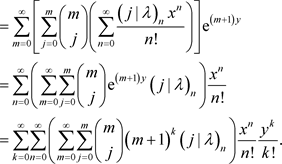
比较上式两端关于项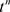的系数即得定理的结论。 □

文章引用

秦 松. 完全退化的Poly-Genocchi多项式
Fully Degenerate Poly-Genocchi Polynomials[J]. 理论数学, 2020, 10(04): 345-355. https://doi.org/10.12677/PM.2020.104044

参考文献