Advances in Applied Mathematics
Vol.04 No.02(2015), Article ID:15307,9
pages
10.12677/AAM.2015.42022
The
 Module of Quantum Electrodynamics on Planar Binary Tree
Module of Quantum Electrodynamics on Planar Binary Tree
Miaohao Jiang, Beishang Ren*, Ruju Zhao, Junwei Liu
School of Mathematical and Statistical Sciences, Guangxi Teachers Education University, Nanning Guangxi
*通讯作者。
Email: Jiangmiaohao@163.com, *beishangen@126.com
Received: May 5th, 2015; accepted: May 22nd, 2015; published: May 27th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Using the combination of Feynman diagrams and the planar binary tree, the renormalization group of QED was defined and the
 module of semidirect product of the group, the semidirect coproduct of the
module of semidirect product of the group, the semidirect coproduct of the
 module, the spread of the
module, the spread of the
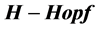 module on the planar binary tree and the
module on the planar binary tree and the
 module with charge were pointed out. Finally it concluded the
module with charge were pointed out. Finally it concluded the
 module of quantum electrodynamics and the renormalization coaction of electron and photon.
module of quantum electrodynamics and the renormalization coaction of electron and photon.
Keywords: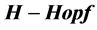 Module, Quantum Electrodynamics, Semidirect Coproduct, Renormalization Coaction
Module, Quantum Electrodynamics, Semidirect Coproduct, Renormalization Coaction

在平面二元树族上的量子电动力学的 模
模
江妙浩,任北上*,赵汝菊,刘君伟
广西师范学院数学与统计科学学院,广西 南宁
Email: Jiangmiaohao@163.com, *beishangen@126.com
收稿日期:2015年5月5日;录用日期:2015年5月22日;发布日期:2015年5月27日

摘 要
利用费曼图和平面二元树的结合,定义了QED的重正化群并指出群上半直积的 模和
模和 模的半直余积,平面二元树上的
模的半直余积,平面二元树上的 模的传播及带电的
模的传播及带电的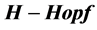 模,最后得出量子电动力学的
模,最后得出量子电动力学的 模及电子和量子的重正化余作用。
模及电子和量子的重正化余作用。
关键词 : 模,量子电动力学,半直余积,重正化余作用
模,量子电动力学,半直余积,重正化余作用

1. 引言
随着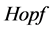 代数理论发展的日益完善,它已不再是一个孤立的体系,它与数学的许多其它领域建立了紧密的联系,在图论、数学物理、离散数学等学科中的应用日趋广泛。近二十多年来,用图的性质去研究代数学结构是一个比较热门的话题。随着Nata等人于1940年所发表的关于拼方的文章,创立了电视网络上的一种数学理论,打开了现代图论研究的序幕。1988年,Istvan Beck首次提出了交换环的零因子图。并系统的研究了这类图的着色数,从而刻画了所有着色数小于4的有限环[1] 。1994年,Schmitt WR在完全图上建立了关联
代数理论发展的日益完善,它已不再是一个孤立的体系,它与数学的许多其它领域建立了紧密的联系,在图论、数学物理、离散数学等学科中的应用日趋广泛。近二十多年来,用图的性质去研究代数学结构是一个比较热门的话题。随着Nata等人于1940年所发表的关于拼方的文章,创立了电视网络上的一种数学理论,打开了现代图论研究的序幕。1988年,Istvan Beck首次提出了交换环的零因子图。并系统的研究了这类图的着色数,从而刻画了所有着色数小于4的有限环[1] 。1994年,Schmitt WR在完全图上建立了关联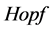 代数结构,开创了
代数结构,开创了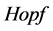 代数与图论的研究 [2] [3] 。1999年Anderson与M. Nseer发表了一篇关于环的性质与零因子图的性质之间是如何相互影响的论文 [4] ,1997年邓汉元等人给出了二元树族的
代数与图论的研究 [2] [3] 。1999年Anderson与M. Nseer发表了一篇关于环的性质与零因子图的性质之间是如何相互影响的论文 [4] ,1997年邓汉元等人给出了二元树族的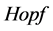 代数结构 [5] 。2005年赵燕提出了完全图与完全二部图及完全
代数结构 [5] 。2005年赵燕提出了完全图与完全二部图及完全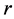 部图的
部图的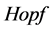 代数结构并指出它们分别与一元二元及
代数结构并指出它们分别与一元二元及 元多项式
元多项式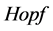 代数同构 [6] 。
代数同构 [6] 。
 代数与图论是数学中的两个非常重要的分支,它们不仅内涵丰富,而且在许多其它数学分支(如组合数学、数学物理、自动机理论以及几何学等)中也有重要作用。研究的
代数与图论是数学中的两个非常重要的分支,它们不仅内涵丰富,而且在许多其它数学分支(如组合数学、数学物理、自动机理论以及几何学等)中也有重要作用。研究的 模图结构,主要是通过
模图结构,主要是通过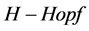 模的某些特征去研究其图结构;反过来,也使用图性质研究的
模的某些特征去研究其图结构;反过来,也使用图性质研究的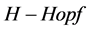 模一些性质。它提供了一种研究数学问题的新方法,从而使得
模一些性质。它提供了一种研究数学问题的新方法,从而使得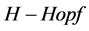 模与图之间相互促进,共同发展。本文是在文献 [7] 中加以研究的,进一步把平面二元树与量子电动力学相结合,将会对
模与图之间相互促进,共同发展。本文是在文献 [7] 中加以研究的,进一步把平面二元树与量子电动力学相结合,将会对 模理论的研究、应用和发展有重要的意义。
模理论的研究、应用和发展有重要的意义。
所谓的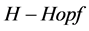 模,文 [8] 中作了如下的定义:设
模,文 [8] 中作了如下的定义:设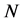 是一个向量空间,
是一个向量空间, 是一个代数,
是一个代数, 是一个
是一个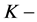 同态,使得下两式成立即:
同态,使得下两式成立即: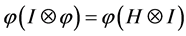 ,
, ,则
,则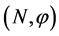 是一个左
是一个左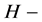 模。设
模。设 是一个向量空间,
是一个向量空间,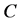 是一个余代数,
是一个余代数,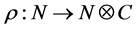 是一个
是一个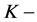 同态,使得下两式成立即:
同态,使得下两式成立即: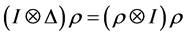 ,
,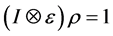 ,则
,则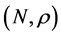 是一个右
是一个右 余模。设
余模。设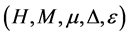 是一个
是一个 代数,
代数,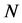 是一个右
是一个右 模,
模,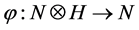 是一个
是一个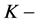 同态,
同态, 是一个右
是一个右 余模,
余模,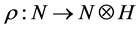 是一个
是一个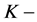 同态,如果
同态,如果 是一个余代数同态或
是一个余代数同态或 是一个代数同态或
是一个代数同态或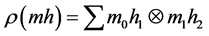 ,则
,则 是一个右
是一个右 模。
模。
量子电动力学,简称为QED (quantum electrodynamics),它主要研究电磁场与带电粒子相互作用的基本过程,两个带电粒子(如两个电子)是通过相互交换光子而相互作用的,这种交换可以有很多种不同的方式,最简单的是其中一个电子发射出一个光子,另一个电子吸收这个光子。稍为复杂一点的是一个电子发射一个光子后,那光子又可以变成一对电子和正电子,这个正负电子对可以随后一起湮灭为光子,也可以由其中的那个正电子与原先的一个电子湮灭,使得结果看起来像是原先的电子运动到了新产生的那个电子的位置,所有这些复杂的过程最终表现为个电子之间的相互作用,计算表明,不同复杂程度的交换方式,对最终作用的贡献是不一样的,它们的贡献随着过程中的光子的吸收或发射次数呈指数式下降,而这个指数的底正好就是精细结构常数,即任何电磁现象可以用精细结构常数的幂级数来表示。
在量子电动力学的范围内,可以把带电粒子与电磁场相互作用当作微扰来处理光的吸收和受激发射问题,但不能处理光的自发射问题,原子中处于激发态的电子是量子力学中的定态,没有辐射场作为微扰,这就不会发生跃迁。
理查德·费曼(1918~1988)是现代及至有史以来最受爱戴的科学家之一,他在量子电动力学领域以最卓越的科学贡献获得了诺贝尔物理奖,这称为“第二个犹拉克”,他发明了费曼图(Feynman Diagram),不但能以直观的方式表达了客观现象,同时也可以对数学进行分析和推导,它把很长很费力的而且很容易产生代数差错的运算加以概括,并把它们按照一定的规则来转换成很简单的过程。用哈密顿量H所构成S矩阵元来描述微观粒子所组成的系统散射或反应过程,在S矩阵元中提出一个反映由初态向末态转化过程中能量动量守恒因子 后,便得到M矩阵元,具体物理过程的跃迁几率直接与
后,便得到M矩阵元,具体物理过程的跃迁几率直接与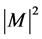 成正比。一个重要而又困难的问题是如何计算各种反应的M矩阵元,“费曼图”就是如何计算M矩阵元的图解方法。给出计算有关过程跃迁几率的计算规则,称为费曼规则。早期的微扰计算也可以得出最低级的近似结果,但为了计算高阶近似就要用重正化方法处理发散问题,用新的理论表述,费曼规则就是最常用的方法。
成正比。一个重要而又困难的问题是如何计算各种反应的M矩阵元,“费曼图”就是如何计算M矩阵元的图解方法。给出计算有关过程跃迁几率的计算规则,称为费曼规则。早期的微扰计算也可以得出最低级的近似结果,但为了计算高阶近似就要用重正化方法处理发散问题,用新的理论表述,费曼规则就是最常用的方法。
本文首先介绍了重正化群和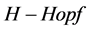 模的半直余积,结合费曼图,定义了QED的重正化群和群上半直积的
模的半直余积,结合费曼图,定义了QED的重正化群和群上半直积的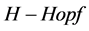 模;其次介绍平面二元树上的
模;其次介绍平面二元树上的 模的传播;再次描述了树上带电的
模的传播;再次描述了树上带电的 模;最后描述平面二元树上的QED的
模;最后描述平面二元树上的QED的 模和余作用,电子和量子的重正化余作用。
模和余作用,电子和量子的重正化余作用。
2. 重正化群和 模的半直余积
模的半直余积
2.1. 费曼图
矩阵M的每一项都与一定的费曼图联系起来,由此确定的图,可以根据“费曼规则”写出相应矩阵元的表达式,而且能清楚地解释这过程的物理现象。
费曼图是用一根带箭头的实线代表电子,带反箭头的实线代表正电子,波浪线代表光子。电子、正电子和光子的每一次相互作用,都用交于一点的两根实线(箭头分别指向和指离支点)和一根波浪线来描写,这支点称为作用顶点。代表初态或末态的线是有一头连接顶点,称为外线,而介于两个顶点之间的线称为内线,内线描写传递相互作用的中间过程的粒子,称为虚粒子。在任一费曼图中,沿实线箭头方向移动,实线或者联成圈或者由外线引向另一外线,它不会在任一顶点终止,这反映了在反应过程中电子数是守恒的。在任何一个图上多增加一条内线,都会使该图的贡献降低一个系数,该系数大致等于一个基
本常数,称为“精细结构常数”,约为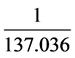 。粒子从空间中一点运动到另一点的每一条可能的路径
。粒子从空间中一点运动到另一点的每一条可能的路径
对应一个数,称之为振幅。费曼图的顶点数称为费曼图的级数,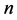 级费曼图代表M矩阵展开式中Mn的一项。
级费曼图代表M矩阵展开式中Mn的一项。
例如两个电子的散射过程,它的二级费曼图(如图1)它描写一个电子先放出一个光子,这带有一定能量的光子传递到另一电子,并被后一个电子所吸收,这样,两个电子的电磁散射,不是它们的直接作用,也不是超距作用,而是由电子与电磁场的相互作用,透过发射和吸收光子的过程来实现。
当两个电子(以直线表示)碰撞时,它们交换光子(以波浪线表示),在图1(a)中,碰撞的电子交换一个光子,在图1(b)中,交换两个光子,在图1(c)中,交换许多光子。
 (a) (b) (c)
(a) (b) (c)
Figure 1. Feynman diagram
图1. 费曼图
2.2. QED的重正化群
这部分介绍电子的重正化群及重正化过程,类似的,也有量子的重正化群及其过程 [9] - [12] 。
定义1 一个电子的重正化群是在直积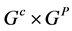 下的由一对
下的由一对 构成的半直积
构成的半直积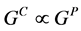 ,且满足条件
,且满足条件 ,
, 。
。
定义2 一个重正化过程是在 上的
上的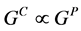 的右作用,且满足以下条件:
的右作用,且满足以下条件:
1) 通过 嵌入
嵌入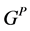 ;
;
2) 投射到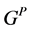 上,且
上,且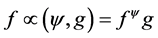 。
。
类似地,一个量子的重正化群是群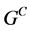 本身;而它的重正化过程是
本身;而它的重正化过程是 上的作用,且
上的作用,且 是
是 的子群,
的子群,

其中 ,且
,且 ,
,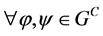 。
。
2.3. 群上半直积的 模
模
设 分别是费曼空图和重正化振幅,选择合适的费曼的图(这里我们先择平面二元树)可以重建空图,重正化传播及正重化群的元素(看文献 [11] - [14] )。
分别是费曼空图和重正化振幅,选择合适的费曼的图(这里我们先择平面二元树)可以重建空图,重正化传播及正重化群的元素(看文献 [11] - [14] )。
如果是两个群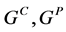 ,则
,则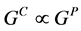 也是群,分别记为
也是群,分别记为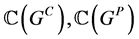 和
和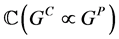 。它们都是
。它们都是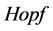 代数。在卷积的作用下,有以下代数同构:
代数。在卷积的作用下,有以下代数同构:
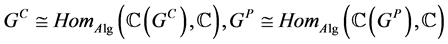 ,
,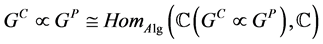
下面是构造 模
模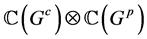 和
和 上的余作用。
上的余作用。
设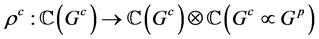 和
和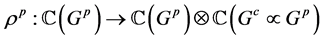 ,对偶于的
,对偶于的 和
和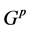 群作用,即有
群作用,即有 和
和 ,其中
,其中 ,即
,即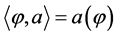 ,也可记为
,也可记为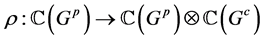 ,它的余作用对偶于
,它的余作用对偶于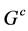 的作用,即
的作用,即 。
。
这样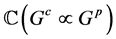 是
是 模,记为
模,记为 ,且满足以下条件:
,且满足以下条件: 对偶于群作用
对偶于群作用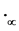 ,即
,即 ,其中是一个模同态即
,其中是一个模同态即 。
。
而且,在 上
上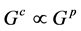 的作用对偶于余作用
的作用对偶于余作用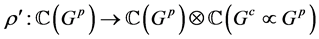 ,
,
即有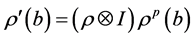 。类似的,线性映射
。类似的,线性映射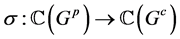 对偶于余圈
对偶于余圈 ,则
,则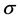 满足下面等式:
满足下面等式:
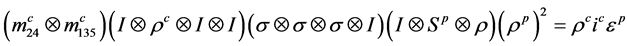
其中, 是
是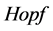 代数
代数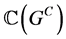 上乘法
上乘法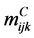 的作用位置,
的作用位置, 是
是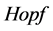 代数
代数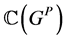 上的反积元,
上的反积元, ,
,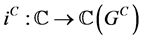 是
是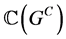 上的单位,
上的单位, 是
是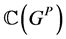 上的余单位。这种情况还有一个等式成立即:
上的余单位。这种情况还有一个等式成立即: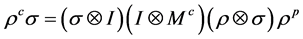 。
。
在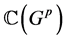 上
上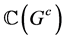 的余作用对偶于作用
的余作用对偶于作用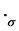 是一个模同态
是一个模同态 ,即
,即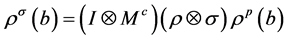 。
。
2.4.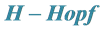 模的半直余积
模的半直余积
设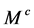 和
和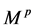 是两个
是两个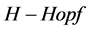 模,
模,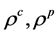 分别是它们的结构映射,设
分别是它们的结构映射,设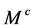 从右边作用于
从右边作用于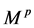 ,余作用
,余作用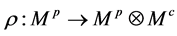 ,且满足如下关系:
,且满足如下关系:
 , (1)
, (1)
 , (2)
, (2)
其中 是位置2和位置4作用,结果放在位置3的乘法;
是位置2和位置4作用,结果放在位置3的乘法;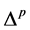 是余积。这样半直余积
是余积。这样半直余积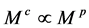 是
是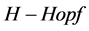 模,且
模,且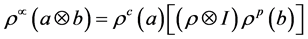 ,
, 余单位
余单位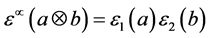 。
。
在文献 [11] [12] [15] ,Molnar已证明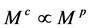 是一个
是一个 代数,反积元是
代数,反积元是 。
。
引理1 设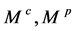 是两个
是两个 模,
模,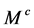 对
对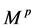 作用如上述(1) (2),如果存在一个映射
作用如上述(1) (2),如果存在一个映射 ,且有
,且有 ,即
,即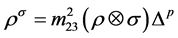 ,使得
,使得
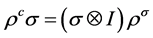 (3)
(3)
则 。
。
证明:由Sweedler的记法,得 ,
,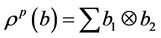 ,
,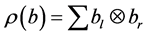 。
。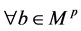
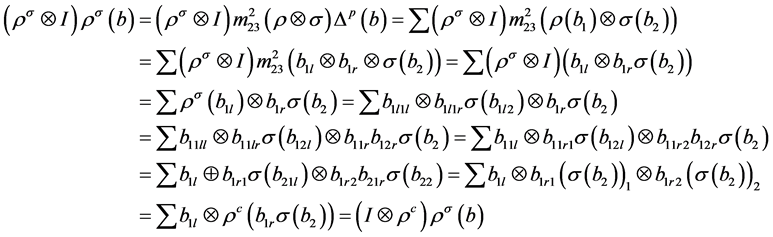
所以 。
。
3. 平面二元树上的 模的传播
模的传播
在这部分我们将介绍树上的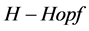 模对偶于电子和量子的传播,它们都是重正化群作用的集合。这些对应于带有积的群和带有余积的非交换同类环,我们将证明它们是
模对偶于电子和量子的传播,它们都是重正化群作用的集合。这些对应于带有积的群和带有余积的非交换同类环,我们将证明它们是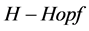 模,对它们的定义主要是通过平面二元树上的积“over and under”[11] [12] [16] 。
模,对它们的定义主要是通过平面二元树上的积“over and under”[11] [12] [16] 。
3.1. 修剪余模(The Pruning Comodules)
定义3 设 是一个线性空间,映射
是一个线性空间,映射 对偶于运算
对偶于运算 和
和 ,即:
,即: ,
,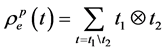 。余单位
。余单位 对偶于单位元
对偶于单位元 ,且
,且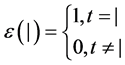 ,则称
,则称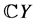 具有两种不同结构的余模。
具有两种不同结构的余模。
定义4 设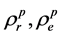 分别是修剪树的左边和右边的树枝,并把它们放在一边,且有如下运算:
分别是修剪树的左边和右边的树枝,并把它们放在一边,且有如下运算: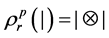 ,
,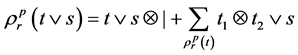 ;类似的,
;类似的, ,
,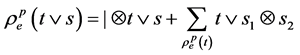 ,则称
,则称 是有两种结构的修剪余模。
是有两种结构的修剪余模。
3.2. 电子和量子传播的 模
模
在文献[17] -[20] 中证明了电子和量子传播的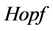 代数。在这部分,我们在树上推广修剪映射
代数。在这部分,我们在树上推广修剪映射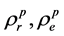 ,根树作为单位元1,我们将得到两种不同的非交换的
,根树作为单位元1,我们将得到两种不同的非交换的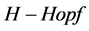 模
模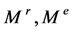 。
。
定义5 设 ,
, 由
由 决定,
决定,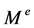 由
由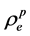 决定,对
决定,对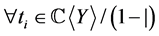 ,
,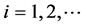 ,有
,有 ,且
,且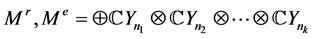 ,则称
,则称 分别是电子和光子传播的
分别是电子和光子传播的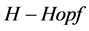 模。
模。
4. 树上带电的 模
模
我们将介绍树上的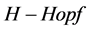 模对偶于作用在电子的重正化群,这类群带有构图法,树上的余积为一个运算。
模对偶于作用在电子的重正化群,这类群带有构图法,树上的余积为一个运算。
4.1. 一个带电的模
设 是一个由平面二元树
是一个由平面二元树 生成的模,对
生成的模,对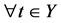 ,有唯一的分解
,有唯一的分解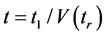 ,映射
,映射 和
和 即
即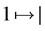 ,它们都是模同态,在
,它们都是模同态,在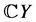 中,度为
中,度为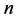 的
的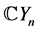 对应于子空间
对应于子空间 ,度为
,度为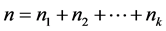 。
。
定义6 我们把带有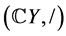 的模
的模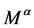 称为带电的模,且根树
称为带电的模,且根树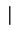 的单位元为1。
的单位元为1。
4.2. 一个带电的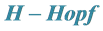 模
模
定义7 定义一个余映射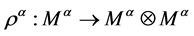 和一个余作用
和一个余作用 ,作为线性运算满足以下关系:
,作为线性运算满足以下关系:
1) ,
,
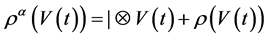

2)
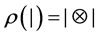
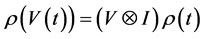
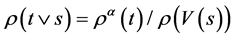
设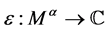 是一线性映射,且
是一线性映射,且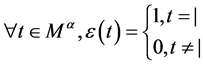 。
。
定理1 模 是一个
是一个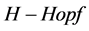 模,且
模,且 是一个右
是一个右 余作用即
余作用即 。
。
证明:首先,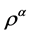 是保
是保 分层的,即
分层的,即 ,
,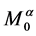 表示树,这样
表示树,这样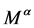 是联通的。由定义5知,
是联通的。由定义5知, 是一个
是一个 模。
模。
先用数学归纳法证明运算 定义一个
定义一个 的左
的左 余作用
余作用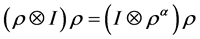
当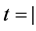 时,等式成立。假设当树的序为
时,等式成立。假设当树的序为 时等式
时等式 是成立的,则当树的序为
是成立的,则当树的序为 时,有
时,有

设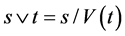 的序是
的序是 ,
, ,则
,则 和
和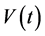 的序小于或等于
的序小于或等于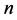 。由Sweedler的符号,得
。由Sweedler的符号,得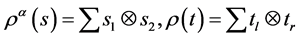 。
。
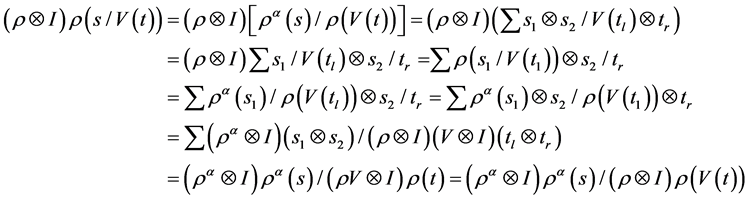
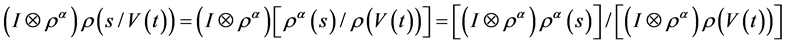
由归纳假设,得等式成立即 。
。
下面我们用数学归纳法证明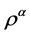 是满足余结合的,即
是满足余结合的,即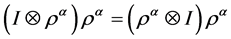 。
。
当 时,等式成立。假设当树的序为
时,等式成立。假设当树的序为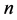 时等式
时等式 是成立的,则当树的序为
是成立的,则当树的序为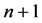 时,有
时,有
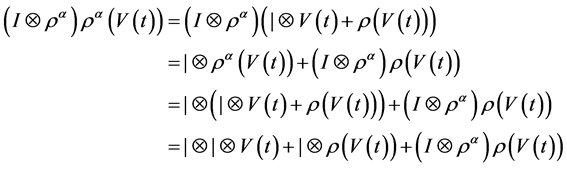
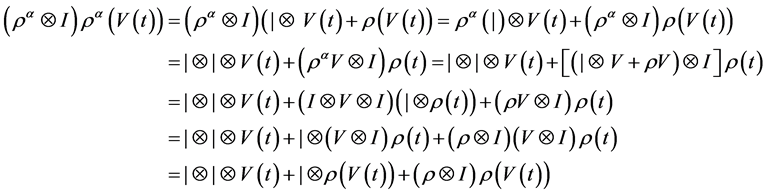
又因为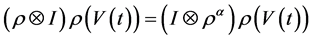 ,所以
,所以 。
。
4.3. 一个非交换的带电的 模
模
设 是一个由树
是一个由树 生成的非交换的模,则带电模
生成的非交换的模,则带电模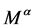 是
是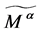 的交换商群,由定义6知,
的交换商群,由定义6知,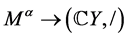 是同构,进而得出
是同构,进而得出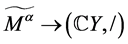 是同构的。由定义7知,由
是同构的。由定义7知,由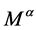 上的运算
上的运算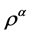 和
和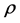 诱导出
诱导出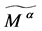 上的运算
上的运算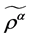 和
和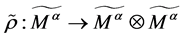 。
。
定理2 模 是一个分层联通非交换的
是一个分层联通非交换的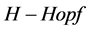 模。
模。
证明:由于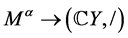 同构,
同构,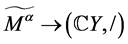 同构,所以
同构,所以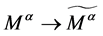 同构,且
同构,且 和
和 ,故由定理1,得出定理成立。
,故由定理1,得出定理成立。
5. 平面二元树上的QED的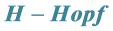 模和余作用
模和余作用
我们将利用第3,4部分定义的运算和第2部分的描述,介绍树上的重正化余作用及QED的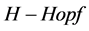 模。
模。
5.1. 电子和光子的余作用
由于 ,则
,则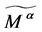 上的余作用
上的余作用 可写成
可写成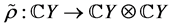 ,
, 是由模
是由模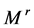 和
和 生成的集合,
生成的集合,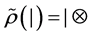 ,
, 推广为两个集合
推广为两个集合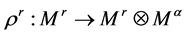 ,
,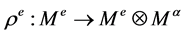 ,即对
,即对
 ,
,
 ,
,
且 ,
,
其中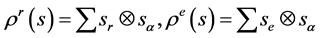 。
。
引理2 1) 映射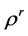 和
和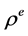 是右
是右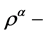 余作用,即满足
余作用,即满足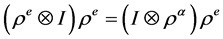 ,
,
 .
.
2) 分别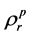 和
和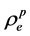 用代替
用代替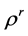 和
和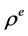 ,即满足
,即满足 ,
,
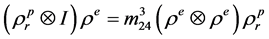 .
.
证明:只需证第一情况。由于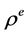 是右
是右 余作用,故在单树上是成立的,即
余作用,故在单树上是成立的,即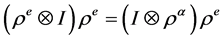 。在积
。在积 上,有:
上,有:
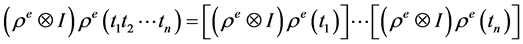 ,
,
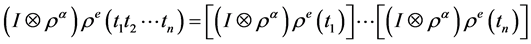
所以是成立的。
下面用数学归观纳法证明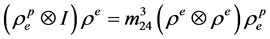 。
。
当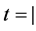 时,等式成立。假设当树的序为
时,等式成立。假设当树的序为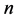 时等式
时等式 是成立的,则树
是成立的,则树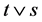 的序为
的序为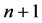 时,有
时,有
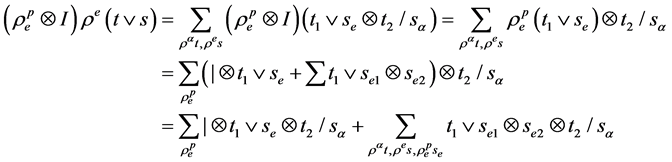

对任意树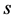 ,有
,有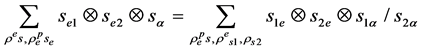 。
。
最后在积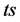 上证明等式
上证明等式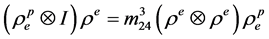 成立
成立
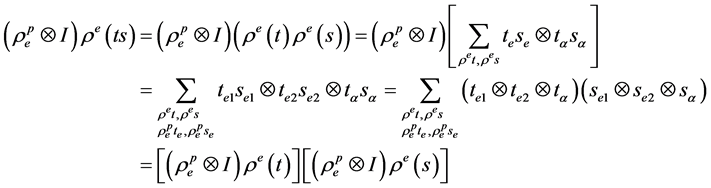
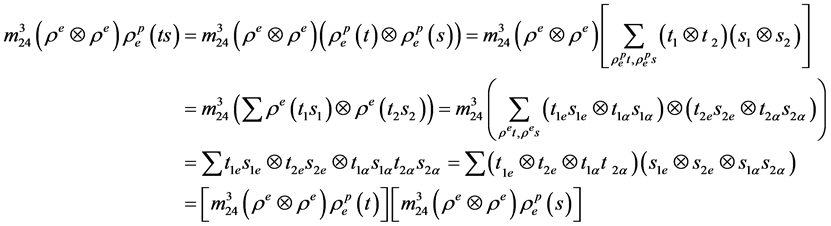
由归纳假设得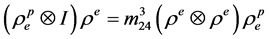 是成立的。
是成立的。
5.2. QED的 模
模
文[16] [21] [22] 证明存在一个QED的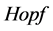 代数,且是分层联通的,作者在此基础上,推广得到一个QED的
代数,且是分层联通的,作者在此基础上,推广得到一个QED的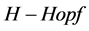 模。
模。
在(2.4)我们定义的一个半直余积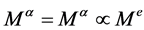 ,且满足以下关系:
,且满足以下关系:
 ,
,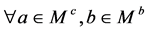 ,
, ,这样
,这样 是
是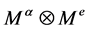 ,是一个
,是一个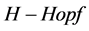 模。
模。
下面定义余映射: ,即
,即

显然,满足这个余映射的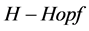 模是QED的
模是QED的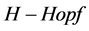 模。
模。
基金项目
广西研究生教育创新计划资助项目(JGY2014092);新世纪广西高等教育教学改革工程A类项目(2012JGA162);2014年度校级教学方法改革专项立项项目;2014年度校级新增博士授权教育学学科建设资助校级科研项目;2014年度校级精品视频公开课立项项目;2015年度校级课堂改革专项课题。
文章引用
江妙浩,任北上,赵汝菊,刘君伟, (2015) 在平面二元树族上的量子电动力学的H-Hopf模
The H-Hopf Module of Quantum Electrodynamics on Planar Binary Tree. 应用数学进展,02,172-181. doi: 10.12677/AAM.2015.42022
参考文献 (References)
- 1. Beck, I. (1988) Coloring of commutative rings. Journal of Algebra, 116, 208-226.
- 2. Schmitt, W.R. (1994) Incidence Hopf algebras. Journal of Pure and Applied Algebra, 96, 299-330.
- 3. Schmitt, W.R. (1995) Hopf algebra methods in graph theory. Journal of Pure and Applied Algebra, 101, 77-90.
- 4. Anderson, D.F. and Livingston, P.S. (1999) The zero-divisor graph of a commutative ring. Algebra, 217, 434-447.
- 5. 邓汉元, 胡国权, 何国梁 (1998) 二元树族的H-Hopf代数结构. 湖南大学学报(自然科学学报), 3, 1-3.
- 6. 赵燕 (2005) 完全图与完全二部图上的H-Hopf代数结构. 曲阜师范大学学报(自然科学版), 3, 25-29.
- 7. 江妙浩, 任北上, 赵汝菊 (2015) 平面二元树族上的H-Hopf模结构. 广西师范院学报(自然科学学报), 3, 21-23.
- 8. Dascalescu, S., Nastasescu, C. and Raianu, S. (2000) Hopf algebra: An introduction. CRC Press, Boca Raton.
- 9. Brouder, Ch. (2000) On the trees of quantum fields. The European Physical Journal C, 12, 535-549.
- 10. Grossman, R. and Larson, R.G. (1989) Hopf algebraic structure of families of trees. Journal of Algebra, 126, 184-210.
- 11. Brouder, Ch. and Frabetti, A. (2001) Renormalization of QED with planar binary trees. European Physical Journal C, 19, 715-741.
- 12. Brouder, Ch. and Frabetti, A. (2003) QED Hopf algebra on planar binary trees. Journal of Algebra, 267, 298-322.
- 13. Connes, A. and Kreimer, D. (2000) Renormalization in quantum field theory and the Riemann-Hilbert problem I: The Hopf algebra structure of graphs and the main theorem. Communications in Mathematical Physics, 210, 249-273.
- 14. Molnar, R.K. (1977) Semi-direct products of Hopf algebras. Journal of Algebra, 47, 29-51.
- 15. Itzykson, C. and Zuber, J.B. (1980) Quantum field theory. McGraw-Hill, New York.
- 16. Loday, J.L. (2002) Arithmetree. Journal of Algebra, 258, 275-309.
- 17. Kreimer, D. (1998) On the Hopf algebra structure of perturbative quantum field theories. Advances in Theoretical and Mathematical Physics, 2, 303-334.
- 18. Loday, J.L. and Ronco, M.O. (1998) Hopf algebra of the planar binary trees. Advances in Mathematics, 139, 293-309.
- 19. Foissy, L. (2002) Les algèbres de Hopf des arbres enracinés décorés I. Bulletin des Sciences Mathématiques, 126, 193- 239.
- 20. Holtkamp, R. (2003) Comparison of Hopf algebras on trees. Archiv der Mathematik, 80, 368-383.
- 21. Loday, J.L. and Ronco, M.O. Order structure on the algebra of permutations and planar binary trees. Journal of Algebraic Combinatorics, to Appear.
- 22. Peskin, M.E. and Schroeder, D.V. (1995) An introduction to quantum field theory. Perseus Books Pub. L.L.C., New York.