 Dynamical Systems and Control 动力系统与控制, 2013, 2, 69-72 http://dx.doi.org/10.12677/dsc.2013.24012 Published Online October 2013 (http://www.hanspub.org/journal/dsc.html) Design and Realization of State Feedback Predictive Control Simulation Software Based on Matlab Feng Guan Collection and Reading Department, National Library of China, Beijing Email: guanfeng1111@163.com Received: Sep. 22nd, 2013; revised: Oct. 20th, 2013; accepted: Oct. 27th, 2013 Copyright © 2013 Feng Guan. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Abstract: This article first introduces the basic principle and characteristics of the State Feedback Predictive Control (SFPC) algorithm. Combined with matlab GUI interface technology, the State Feedback Predictive Control simulation software is designed. And with first-order system and second-order system, it shows State Feedback Predictive Control algorithm simulation analysis. The results show that the Predictive Control algorithm for nonlinear system static and dynamic performance has got fast response resistance, smaller steady state error and good robustness control effect. Keywords: Matlab; State Feedback Predictive Control; Simulation; Design 基于 Matlab 的状态反馈预测控制仿真软件设计与实现 管 峰 中国国家图书馆典藏阅览部,北京 Email: guanfeng1111@163.com 收稿日期:2013 年9月22 日;修回日期:2013年10月20日;录用日期:2013 年10 月27日 摘 要:本文首先阐述了状态反馈预测控制(State Feedback Predictive Control, SFPC)算法的基本原理和特点,结 合matlab GUI 人机界面接口技术,设计开发了状态反馈预测控制仿真软件,并且以一阶系统和二阶系统为例, 进行状态反馈预测控制算法仿真分析,结果表明,该预测控制算法对于非线性系统的静态和动态性能具有快速 响应性、稳态误差小以及鲁棒性好等良好控制效果。 关键词:Matlab;状态反馈预测控制;仿真;设计 1. 引言 由于很多算法依赖被控对象精确的数学模型,而 工业过程的对象往往比较复杂,具有非线性、时变性 和不确定性,多输入多输出并有多重滞后,很难建立 精确的数学模型,针对工业过程的上述特点,人们开 始试图寻找对模型精度要求低,在线计算方便,控制 质量好的控制方案。预测控制就是在这种背景下发展 起来的。它比较适合工业过程的特点,并且具有良好 的控制性能和抗干扰能力,自出现以来,便迅速地在 石油化工等复杂工业过程中得到了成功应用[1]。 预测控制技术如动态矩阵控制(Dynamic Matrix Control, DMC)、广义预测控制(Generalized Predictive Control, GPC))和状态反馈预测控制(State Feedback Predictive Control, SFPC)等算法,都以模型预测、反 馈校正和滚动优化的特点越来越受到广大科技工作 者的重视[2]。经 过20 多年的发展与应用,已经产生从 线性时不变系统,扩展应用到非线性、时变系统的多 种新的预测控制技术,预测控制成为控制工程界研究 Copyright © 2013 Hanspub 69  基于 Matlab的状态反馈预测控制仿真软件设计与实现 的一个热点[3]。 本文主要是应用状态反馈预测控制算法的特点, 对单输入单输出线性系统仿真及分析。用 MATLAB 程序实现 GUI人机接口界面,并且在该界面中实现状 态反馈控制系统的仿真,很好地对该预测控制算法的 控制效果进行了展示。 2. 状态反馈预测控制 状态反馈和输出反馈属于状态空间中的系统反 馈。将系统的状态反馈到输入端就是状态反馈,并与 控制输入端一起作用到系统。状态反馈预测控制模 型,如图1所示。 状态反馈预测控制(State Feedback Predictive Control, SFPC)算法是一种用被控对象的阶跃响应特 性来描述系统动态模型的预测控制算法。若其被控过 程的状态是可以实际测量的,那么它就可以引入状态 反馈,这时,宜采用状态空间模型,进行预测计算[4]。 当模型准确且无干扰时(v = 0),虽然输出反馈通道无 作用相当于断开,但是状态反馈通道仍是闭合的,那 么,闭环极点与被控过程的极点是不同的,是这种结 构的系统可用于被控过程不稳定的状况。实测状态中 包含了未知干扰v的信息是状态反馈的另一个特点, 状态反馈相就当于引入了未知干扰的前馈,使闭环系 统抑制干扰的能力得到了很大的提高。SFPC 保留了 其他预测控制算法的一个特点,即如果闭环控制系统 是稳定的,则无论模型是否准确,对于阶跃输入(给定 值或干扰)均是无稳态偏差的,并有较强的鲁棒性[5]。 3. 在MATLAB 中GUI简介 图形用户界面(Graphical User Interface,简称 GUI,又称图形用户接口)是指采用图形方式显示的计 算机操作用户介面。准确来说 GUI 就是屏幕产品的视 觉体验和互动操作部分。GUI 是一种结合计算机科学、 美学、心理学、行为学,及各商业领域需求分析的人 机系统工程,强调人–机–环境三者作为一个系统进 行总体设计[6]。 MATLAB 图形用户界面开发环境 GUIDE (MATLAB’s Graphical User Interface Development En- vironment)。MATLAB 为用户开发图形界面提供了一 个方便高效的集成环境。上述所有工作都能够使用 GUIDE 方便的实现。GUIDE 主要是一个界面设计工 Figure1. State feedback predictive control schematic 图1. 状态反馈预测控制示意图 具集,MATLAB将所有 GUI 支持的用户控件都集成 在这个环境中并提供界面外观,属性和行为响应方式 的设置方法。GUIDE将用户保存设计好的 GUI 界面 保存在一个 FIG 资源文件中,同时还能够生成包含 GUI 初始化和组件界面布局控制代码的M文件。这个 M文件为实现回调函数(当用户激活 GUI 某一组件时 执行的函数)提供了一个参考框架[7]。虽然使用用户自 己编写的,包含GUI所有发布命令的 M文件也能够 实现一个 GUI,但是使用 GUIDE 执行效率更高:使 用GUIDE 不但能够交互式的进行组件界面布局,而 且能够生成两个用来保存和发布GUI 的文件。 4. 状态反馈预测控制仿真软件设计 4.1. GUI人机接口界面图 用户界面主要分了四大区域,如图 2所示,下面 分别对个区域进行分别介绍: (1) 曲线显示区域:此处用来显示已选择的状态 变量值。 (2) 系统选择:用 Pop-Up 按钮做成的下拉菜单, 可以随意选择系统(一阶系统、二阶系统、三阶系统)。 (3) 参数设置区:用户可以在文本框中设置各个 参数的值。 (4) 行为命令区域:此区域块共有3个按钮,分 别是“plot”,“disturb ”和“close”。点击“plot”按 钮,状态反馈预测控制仿真曲线会如图所示在曲线显 示区域显示。点击“disturb”按钮,会显示加入干扰 后的状态反馈预测控制仿真曲线。点击“close”按 钮 , 可以关闭仿真软件。 4.2. 状态反馈预测控制仿真软件实现 4.2.1. 一阶系统仿真及功能演示 假定一阶系统对象动态模型如下 A d = [0.45], = [1], = [1], Bd Cd D d = 0 状态反馈预测控制仿真曲线如图3所示。 Copyright © 2013 Hanspub 70  基于 Matlab的状态反馈预测控制仿真软件设计与实现 Figure2. GUI graphical interface 图2. GUI图形接口界面 Figure3. First-order system simulation curve 图3. 一阶系统仿真曲线 如图 3所示,各参数值都是程序中赋予的初始值, 他们都可以改变。预测时域p为20 ,输出给定值 sp 为1,建立动态模型的参数值 A d = [0.45],Bd= [1], = [1], Cd D d = 0。此时对预测控制没有加干扰。 (1) 不同预测时域对控制系统的影响 在一阶系统下对单输入单输出(SISO)系统进行状 态反馈预测控制仿真,仿真曲线如图4所示。 由图 4中(a),(b),( c),(d) 所示,我们可以看出,当预 测时域 p = 1 时,系统不能稳定;当预测控制时域p = 3时,虽然最后系统稳定但有振荡;当预测时域p = 5 时,控制效果较好;当预测时域p = 11时,控制效果 最好。所以,取预测时域p = 11 时,控制效果最好。 预测时域的选取对控制系统的稳定性有很大的影响, 预测时域越大时,控制效果越好。而且当预测时域大 于某一值后,控制效果将不再发生变化[8]。 (2) 对一阶系统加入干扰,其他设定值不变,如 图5所示。 如图 5所示,一阶系统加入干扰,状态反馈预测 (a) p = 1 (b) p = 3 (c) p = 5 (d) p = 11 Figure 4. First-order system simulation curve under different forecast time domain 图4. 不同预测时域下一阶系统仿真曲线 Copyright © 2013 Hanspub 71 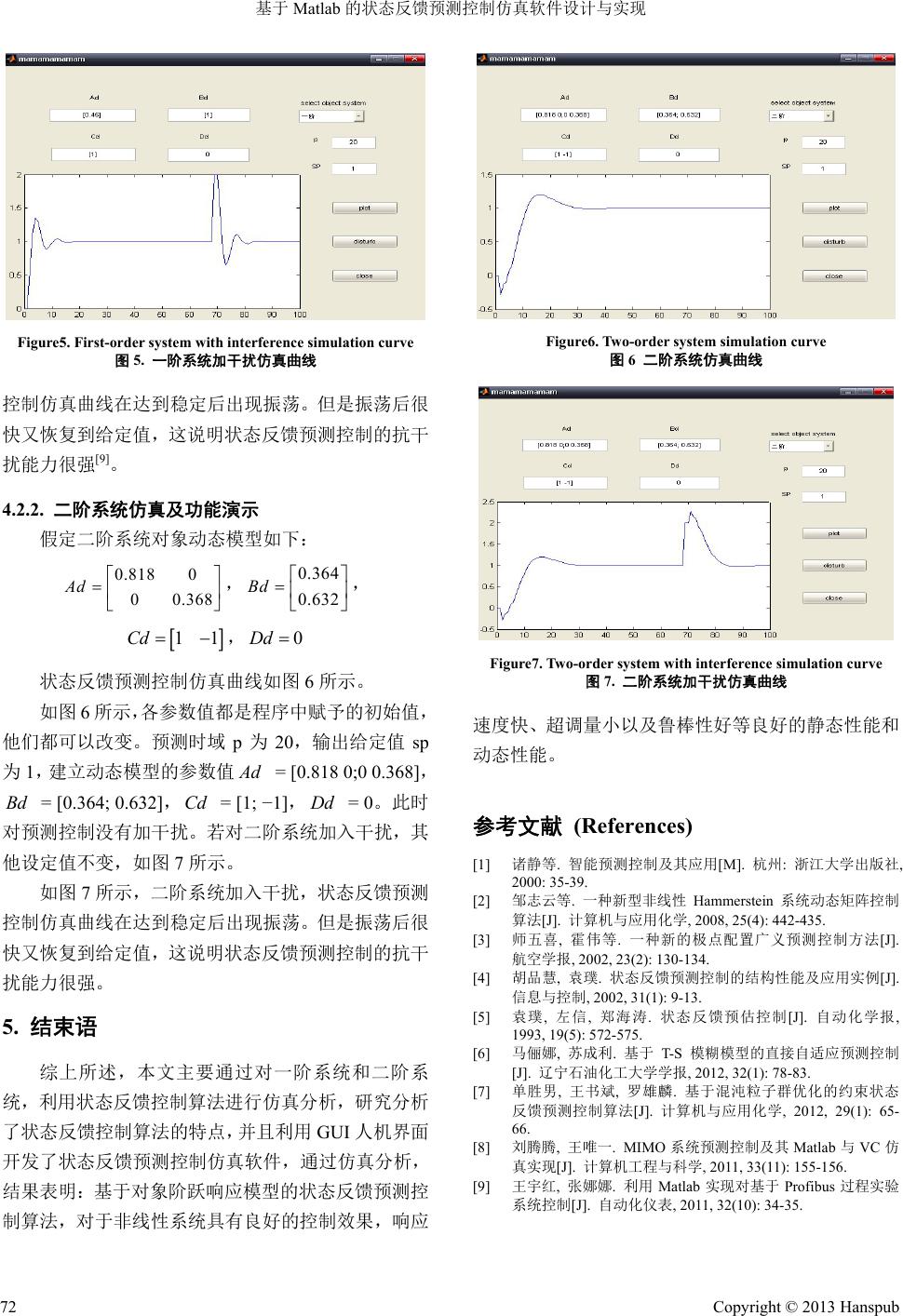 基于 Matlab的状态反馈预测控制仿真软件设计与实现 Copyright © 2013 Hanspub 72 Figure6. Two-order system simulation curve Figure5. First-order system with interference simulation curve 图6 二阶系统仿真曲线 图5. 一阶系统加干扰仿真曲线 控制仿真曲线在达到稳定后出现振荡。但是振荡后很 快又恢复到给定值,这说明状态反馈预测控制的抗干 扰能力很强[9]。 4.2.2. 二阶系统仿真及功能演示 假定二阶系统对象动态模型如下: 0.818 0 00.368 Ad , , 0.364 0.632 Bd 11Cd , 0Dd Figure7. Two-order system with interference simulation curve 状态反馈预测控制仿真曲线如图6所示。 图7. 二阶系统加干扰仿真曲线 如图 6所示,各参数值都是程序中赋予的初始值, 他们都可以改变。预测时域p为20 ,输出给定值 sp 为1,建立动态模型的参数值 A d = [0.818 0;0 0.368], = [0.364; 0.632],Cd = [1; −1], Bd D d = 0。此时 对预测控制没有加干扰。若对二阶系统加入干扰,其 他设定值不变,如图7所示。 速度快、超调量小以及鲁棒性好等良好的静态性能和 动态性能。 参考文献 (References) [1] 诸静等. 智能预测控制及其应用[M]. 杭州: 浙江 大学出 版社 , 2000: 35-39. 如图 7所示,二阶系统加入干扰,状态反馈预测 控制仿真曲线在达到稳定后出现振荡。但是振荡后很 快又恢复到给定值,这说明状态反馈预测控制的抗干 扰能力很强。 [2] 邹志云等. 一种新型非线性 Hammerstein 系统动态矩阵控制 算法[J]. 计算机与应用化学, 2008, 25(4): 442-435. [3] 师五喜, 霍伟等. 一种新的极点配置广义预测控制方法[J]. 航空学报, 2002, 23(2): 130-134. [4] 胡品慧, 袁璞. 状态反馈预测控制的结构性能及应用实例[J]. 信息与控制, 2002, 31(1): 9-13. [5] 袁璞, 左信, 郑海涛. 状态反馈预估控制[J]. 自动化学报, 1993, 19(5): 572-575. 5. 结束语 [6] 马俪娜, 苏成利. 基于 T-S模糊模型的直接自适应预测控制 [J]. 辽宁石油化工大学学报, 2012, 32(1): 78-83. 综上所述,本文主要通过对一阶系统和二阶系 统,利用状态反馈控制算法进行仿真分析,研究分析 了状态反馈控制算法的特点,并且利用GUI 人机界面 开发了状态反馈预测控制仿真软件,通过仿真分析, 结果表明:基于对象阶跃响应模型的状态反馈预测控 制算法,对于非线性系统具有良好的控制效果,响应 [7] 单胜男, 王书斌, 罗雄麟. 基于混沌粒子群优化的约束状态 反馈预测控制算法[J]. 计算机与应用化学 , 2012, 29(1): 65- 66. [8] 刘腾腾, 王唯一. MIMO系统预测控制及其 Matlab 与VC仿 真实现[J]. 计算机工程与科学, 2011, 33(11): 155-156. [9] 王宇红, 张娜娜. 利用 Matlab实现对基于 Profibus 过程实验 系统控制[J]. 自动化仪表, 2011, 32(10): 34-35. |