设为首页 加入收藏 期刊导航 网站地图

Advances in Applied Mathematics
Vol.05 No.03(2016), Article ID:18408,14 pages
10.12677/AAM.2016.53053

Research on Generalized Uncertainty Principles

Xiaotong Wang1, Guanlei Xu2*, Lijia Zhou2, Limin Shao2, Xiaogang Xu1

1Navigation Department of Dalian Navy Academy, Dalian Liaoning

2Ocean Department of Dalian Navy Academy, Dalian Liaoning

Received: Jul. 28th, 2016; accepted: Aug. 19th, 2016; published: Aug. 25th, 2016

Copyright © 2016 by authors and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

ABSTRACT

The uncertainty principle plays an important role in both physics and mathematics, and it also plays an important role in information science. This paper reviewed the Heisenberg’s uncertainty principles, windowed uncertainty principles, logarithmic uncertainty principles, entropic uncertainty principles and so on in the fractional Fourier transform domains and linear canonical transform domains in great details. The development and applications of generalized uncertainty principles were analyzed, and the trend and direction were given as well.

Keywords:Fractional Fourier Transform (FRFT), Linear Canonical Transform (LCT), Uncertainty Principle

广义测不准原理理论研究

王孝通1，徐冠雷2*，周立佳2，邵利民2，徐晓刚1

1海军大连舰艇学院航海系，辽宁 大连

2海军大连舰艇学院军事海洋系，辽宁 大连

收稿日期：2016年7月28日；录用日期：2016年8月19日；发布日期：2016年8月25日

摘 要

测不准原理不仅是物理学中的一个基本问题，也是数学中的一个基本问题，同时对于信息学等多种学科均有较大的影响。从信号处理的角度，本文对分数阶域以及广义分数阶域(线性完整变换域或线性正则变换域)的Heisenberg测不准原理、加窗测不准原理、对数测不准原理、熵测不准原理等理论及其扩展进行了全面分析和综述，与传统测不准原理作了深入分析比较，剖析了广义测不准原理的发展和应用现状，并给出了广义测不准原理尚需进一步研究的问题。

关键词 :分数Fourier变换，线性正则变换，测不准原理

1. 引言

1927年，德国物理学家Heisenberg首次提出了测不准原理(Uncertainty Principle)，又称Heisenberg测不准原理 [1] 。它解释了量子力学存在的基本问题，即不能同时确定两个共轭变量(例如，位置和速度，时间和频率)的测量精度，并且这两个共轭变量准确度的乘积存在下界。Heisenberg测不准原理被证明在很多其它领域(数学、信息学、社会科学等)也是一条通用的自然法则 [2] - [30] ，如应用于时频平面分辨率分析的加窗测不准原理 [4] - [7] ，数学理论中的对数测不准原理 [4] [8] [9] ，量子力学与信息学中的熵(主要包括香农熵、Renyi熵、Tsallis熵、黑洞普朗克熵等)测不准原理 [4] [10] - [22] 等等，这些结论在各自学科领域的理论和应用研究中发挥了重要的作用。同时，也给出了一个重要的结论：在不同的域内，测不准原理具有不同物理含义和不同下限 [23] - [42] ，研究和获得这些下限，可以进一步指导在其相关领域的理论研究和工程应用。

从信号处理的角度，本文对Heisenberg测不准原理、加窗测不准原理、对数测不准原理、熵测不准原理等在分数阶域以及广义分数阶域内(有关分数阶Fourier变换和线性正则变换的内容请读者参考文献 [43] - [45] )的理论及其应用扩展进行了全面分析和综述，与传统测不准原理也作了深入分析比较，并剖析广义测不准原理的发展和应用现状，最后给出广义测不准原理尚需要进一步研究的内容和方向。

2. 信号处理中的测不准原理

在信号处理中，Heisenberg测不准原理具有两层含义：时间分辨率和频率分辨率不能同时无限制地提高，它们的乘积存在一个下限；时间分辨率和频率分辨率之间存在着相互制约的关系，即如果要提高频率分辨率就得降低时间分辨率，反之亦然。

目前多数多分辨率分析/变换方法 [31] - [41] 的分析思想源于测不准原理，即高频区域具有低的频率分辨率和高的时间分辨率，而低频区域具有高的频率分辨率和低的时间分辨率。根据测不准原理等式成立的条件，获得了多种变换的最优基函数，例如短时Fourier变换的高斯窗函数 [42] 、S变换的频变高斯窗函数 [31] - [34] 以及最优小波基函数 [32] - [41] 等等。

在Heisenberg测不准原理的指导下，信号处理研究工作取得了许多成果。然而，随着信号处理技术的进一步发展，人们对测不准原理又有了新的认识。2000年和2004年，在条件概率情况下，L. Cohen得到了较传统测不准原理更小的下限 [6] [7] ，这意味着在某些情况下，可以突破传统测不准原理的束缚，推动了测不准原理进一步深入研究。

在FRFT变换(Fractional Fourier Transform)和LCT变换(Linear Canonical Transform，又称为广义变换)域 [42] - [52] ，一些学者开始探索新变换域的测不准原理 [23] - [30] [53] - [59] [86] ，又称为广义测不准原理。为了便于描述，按照变换域，广义测不准原理可以分为FRFT域的广义测不准原理和LCT域广义测不准原理。

3. FRFT域的广义测不准原理

文献 [23] [24] 首先证明了时间支撑和FRFT域的广义频率支撑的Heisenberg测不准原理，其有效支撑乘积的下限为(为FRFT的变换参数)，但是它只是一种特例，没有给出普遍意义的下限和明确的物理解释。2001年，Shinde等接着给出了任意两个不同FRFT域内实数信号的Heisenberg测不准原理，得到了一个更为严格的下限，其下限不仅与实数信号传统的时间支撑和频率支撑(有效带宽)有关，还与FRFT变换的参数有关，而且还进一步分析了明确的物理意义。但是，这个结论只适合于实数信号 [24] 。在此基础上，我们证明和推导了FRFT域的任意复数信号的Heisenberg测不准原理、对数测不准原理和加窗测不准原理，并给出了其物理分析 [53] ，并且我们也深入探讨了FRFT变换域的广义熵测不准原理 [54] 。此外，我们把任意两个不同FRFT域内实数信号的Heisenberg测不准原理，从一个测不准关系扩展到三个具有严格下限的测不准关系，并给出了各自的物理解释 [55] 。此后，我们又把任意两个不同FRFT域内复数信号的Heisenberg测不准原理，从一个测不准关系扩展到三个具有严格下限的测不准关系，同样给出了各自的物理解释 [86] [87] 。

4. LCT域的广义测不准原理

论文应采用A4幅面进行排版。论文页面设置为：上边距 3 厘米 ，下边距3厘米，左右边距 2 厘米 ；页眉 2 厘米 ，页脚1.5厘米。2008年，Sharma等对文献 [25] 的结果在LCT域内进行了扩展，论证了实数信号的任意两个LCT域内的测不准原理，并给出了带限信号的特例：在两个不同的LCT域内，存在一个实数信号和两个变换参数系，使得该实数信号在这两个LCT域内同时是带限的 [30] 。尽管这一特例是对特殊的LCT变换参数而言，但至少从理论上证明：在新的变换域内，存在这样的情况，可以使得信号分辨率分析得到极大的提高。差不多与Sharma研究工作的同时，我们和Zhao等都进行了类似的工作 [56] [57] 。我们把实数信号的任意两个LCT域的测不准原理扩展为：两个有效支撑之间的测不准原理、两个群延迟之间的测不准原理、一个群延迟和一个有效支撑之间的交叉测不准原理，并给出了新的物理解释 [56] 。Zhao等则把实数信号LCT下Heisenberg测不准原理应用矩的关系进行了重新证明，可以避免Cauchy-Schwartz不等式对特殊LCT参数的无效性 [57] 。另外，针对复数信号，我们把任意复数信号的Heisenberg测不准原理、对数测不准原理、加窗测不准原理以及熵测不准原理在LCT域内进行了扩展 [55] [58] 。文章 [90] 还研究了复信号情况下线性正则域的不确定原理，得到了信号在两个不同线性正则域带宽乘积的下界。该下界与时频协方差相关，已有的Heisenberg不确定原理的下界均可看成是该下界的特殊情况，另外利用该下界可解释线性正则(分数阶傅里叶)域不确定原理中实信号与复信号具有不同下界的现象。在研究过程中，我们还发现这些测不准原理并不那么严密，其下限没有像实数那样严格，而此前，Stern等已经给出了Heisenberg测不准原理在LCT特定参数下的几个特例 [26] [27] 。

此后，我们又把任意两个不同LCT域内复数信号的Heisenberg测不准原理，从一个测不准关系扩展到三个具有严格下限的测不准关系，并给出了各自的物理解释 [86] [87] 。这些已有的工作表明，广义测不准原理均与变换参数有关，可以为广义域的时频分析提供更好更多的选择，只要选择合适的变换参数可获得更高分辨率的分析，而且在某些特定情况下，理论上信号分辨率同时在两个不同变换域内可以没有约束地提高。此外，在信息学和量子力学中，广义域的熵测不准原理又可以提供新的思路，为潜在的应用提供重要的理论基础。因此，无论是从信号处理的角度，还是从物理学对自然界认识的角度，测不准原理都具有重要的理论指导意义和工程应用价值。

5. 不同变换域测不准原理及不等式的比较分析

本节列出了传统的测不准原理关系不等式、新推导的测不准关系不等式等，其中，表1~6分别列出了Shannon熵测不准原理，Rényi熵测不准原理，Heisenberg测不准原理，加窗测不准原理以及对数测不准原理。表7给出了两种不等式：Hausdorff-Young不等式和Pitt不等式。显然，从表中可以看出新推导的不等式与以往给出的不等式(包括传统不等式)的关系和不同，下面就对它们进行了深入分析。

5.1. 广义Heisenberg测不准原理下限参数的有关性

(广义)分数阶Fourier变换域的Heisenberg测不准原理，其下限均与变换参数有关，其物理含义以表1

最后一个不等式(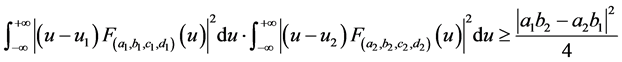)为例，加以分析说明。

Table 1. Heisenberg Uncertainty Principles

表1. Heisenberg测不准原理

传统时频域，Heisenberg测不准原理的下限为1/4。

广义分数阶Fourier变换域，当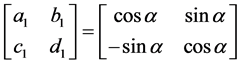和时，Heisenberg测不准原理下限值为。当时，其下限值则为。

Table 2. Shannon Entropic Uncertainty Principles

表2. Shannon熵测不准原理

Table 3. Rényi Entropic Uncertainty Principles

表3. Rényi熵测不准原理

Table 4. Windowed Uncertainty Principles

表4. 加窗测不准原理

Table 5. Logarithmic Uncertainty Principles

表5. 对数测不准原理

理论上，广义分数阶Fourier变换域的Heisenberg测不准原理的下限可以接近于零。如果为零，这一新变换域仅仅是通过单纯尺度变换或调制得到的，这个结论和文献 [30] 结果吻合，不同的是文献 [30] 认为单纯尺度变换或调制得到的变换域为新的变换域，即对于同一信号，它在两个广义分数阶Fourier变换域可同为带限信号。

5.2. Shannon熵测不准原理较传统情况具有更小的下限

(广义)分数阶Fourier变换域的Shannon熵测不准原理具有更小的下限，如表2中下式为例：

只要选择合适的参数和，并考虑到，当、和时，，则求解方程组：

可得到：，。

当时，则广义分数阶Fourier变换域的Shannon熵测不准原理的下限可以达到零。很明显，上述方程组是欠定的，存在无数解。

5.3. 广义Rényi熵测不准原理较传统情况具有更小下限

较传统Rényi熵测不准原理，(广义)分数阶Fourier变换域的Rényi熵测不准原理可以达到更小的下限，如表3中下式：

。

只要选择合适的参数和使成立，则分数阶及广义分数阶Fourier变换域的Rényi熵测不准原理的下限可以达到零。

Table 6. Heisenberg Uncertainty Principles for complex signal

表6. 复数信号的Heisenberg测不准原理

Table 7. Other inequalities (Hausdorff-Young and Pitt Inequalities)

表7. 其他不等式(Hausdorff-Young不等式和Pitt不等式)

同理，当和时，其中，则其下限可为零。

Shannon熵与Rényi熵测不准原理类似，不再详述。

5.4. 广义加窗测不准原理比传统加窗测不准原理具有更小的下限

(广义)分数阶Fourier变换域的加窗测不准原理可以获取比传统加窗测不准原理更小的下限，如表4

中不等式，当和时，则其下限值为，最小下限可为1/4，小于传统下限1。

5.5. (广义)分数阶Fourier变换域的对数测不准原理的下限与变换参数相关

如表5中下式：

只要使，则其下限也可以达到零。

同理，当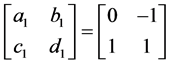和时，其中，则其下限可为零。

综上所述，(广义)分数阶Fourier变换域的时频分析可提供更好更多的选择，只要选择合适的变换参数就可获得更高分辨率的分析，而且在某些特定情况下，信号分辨率在两个不同变换域可以极大地提高。在信息学和量子力学中，新型变换域的熵测不准原理又可以提供新的思路，为潜在的应用提供了重要的理论基础。

值得注意的是，所有连续测不准原理不等式关系当等号成立时，信号几乎均为高斯类型的函数，目前还没有发现特例。

与此同时，我们还发现了许多有待于进一步解决的问题。

6. 测不准原理的进一步研究问题

对于广义域，测不准原理还有很多问题需要进一步研究，特别是离散广义测不准原理、复数信号的广义测不准原理、多维广义测不准原理等等。

6.1. 离散广义测不准原理

目前所公开发表的广义测不准原理都是针对连续信号的，但离散信号与连续信号有许多不同点：首先，在实际工程应用中离散信号的时间支撑和频率支撑都是有限的，而对于连续信号不成立 [60] ，因此，广泛应用于连续信号的数学不等式 [9] [15] (例如广义Pitt不等式、广义Hausdorff-Young不等式等)及其证明方法(例如基于广义Jensen不等式的凹凸理论)都需要进一步完善。其次，目前离散信号的时间支撑和频率支撑的表述还没有一个被广泛接受的统一定义，理论上尚不完善。还有，广义变换离散计算方法、离散性质等还有待进一步分析 [43] 。另外，业已证明：在传统域内，高斯信号不再是离散测不准原理等式成立的条件 [61] - [65] [92] [93] 。

纵观现有的成果，在FRFT、LCT域所对应的离散信号广义测不准原理(包括Heisenberg测不准原理、对数测不准原理、加窗测不准原理、香农熵测不准原理和Renyi熵测不准原理等)尚属空白，而且连续信号和离散信号的Tsallis熵 [66] 和黑洞普朗克熵 [15] 广义测不准原理，目前都还没有文献涉及。

6.2. 复数信号的广义测不准原理

实数和复数的测不准原理在广义域内具有不同的下限 [23] - [30] [53] - [59] ，而这与传统测不准原理的规律相悖 [43] [45] ，我们知道传统测不准原理无论是实数还是复数都具有相同的下限1/4或1/16π2，那么，实数和复数在广义域内确实存在不同的下限，是因为目前的证明和推导存在问题呢？同时现有的工作还表明，复数信号在广义域似乎还没有得到类似于实数信号那样更为严格的下限？目前还没有公开的报道给出明确的答案。这一问题至关重要，对于相关领域问题研究的指导性不言而喻，每一种测不准原理都应只有唯一的准确和严密下限，否则会误导对问题的求证和理解。对于传统的四元复数，Mawardi Bahri等 [67] 进行了相关讨论，不过得到的结论只是纵横方向上的一维测不准原理，并没有反映四元复数本身特性。

另外，由Hilbert变换 [68] - [73] [94] 和广义Hilbert变换 [74] - [76] [94] 生成的复数信号是目前信号处理常用的复数信号形式，而且在信号处理中具有重要的作用，但它不同于传统意义上的复数信号，目前还没有公开的文献论述这类信号的测不准原理。

6.3. 多维广义测不准原理

一直以来，对于多维信号的测不准原理，通常将其投影到多个方向上的一维信号进行独立分析与处理，例如对于图象，传统的小波变换、Fourier变换等将其行列可分离进行变换，对应的测不准原理也就是行列上一维测不准原理的乘积 [2] - [4] 。但是，有些变换方法 [50] [77] 行列是相关的，不可分离，需要采取新的处理方法。实际上，多数信号在不同方向上是相关的(例如，边缘密度函数和x，y两个变量均相关)，在实际工程应用多数情况可以认为它们行列近似独立。对于这类信号，必须考虑不同方向的相关特征 [88] ，因此，多维广义测不准原理是这类信号的处理基础。

6.4. 广义测不准原理的应用

如何把测不准原理应用于多维信号分析。传统的测不准原理 [2] - [20] 还是广义测不准原理 [23] - [30] [53] - [59] ，已在一维信号分析中得到了广泛应用，而对于多维信号分析，如分析二维图象主要限于行列上的独立分析，但是图象具有重要的行列相关性，人类视觉敏感频率信息，也敏感方向信息，如频率相同而方向不同的图象很容易加以区分，因此二维信号的方向和内部维数 [70] [78] 也是图象的重要特征。因此，针对多维的图象信号，如何应用测不准原理进行分辨率分析十分重要，特别是针对图像融合，如何进行高分辨率信息的识别判读是重要的应用方向之一 [79] - [85] 。而且，广义一维和多维测不准原理在一维信号、图象、视频等信号的分析和处理方面是否能够发挥重大的作用呢？ [91] [95] 也需要加以深入研究。

7. 结论

从信号处理的角度，本文对(广义)分数阶Fourier变换域的测不准原理进行了全面分析和综述，包括Heisenberg测不准原理，Shannon熵测不准原理，Rényi熵测不准原理，加窗测不准原理、对数测不准原理、以及几个新的数学不等式等，给出了各种测不准原理的比对和不同表现形式，并剖析了广义测不准原理的发展和应用现状。(广义)分数阶Fourier变换域的测不准原理，其下限均与变换参数有关，选择合适的变换参数可获得更高分辨率的分析，(广义)分数阶Fourier变换域的时频分析也可提供更好更多的选择，而且在某些特定情况下，信号分辨率在两个不同变换域可以极大地提高。对于广义域，还指出了广义测不准原理尚需要进一步研究的内容和方向，特别是离散广义测不准原理、复数信号的广义测不准原理、多维广义测不准原理等等。

基金项目

国家自然科学基金(批准号：61002052，61250006，61273262，61471412)项目资助。

文章引用

王孝通,徐冠雷,周立佳,邵利民,徐晓刚. 广义测不准原理理论研究
Research on Generalized Uncertainty Principles[J]. 应用数学进展, 2016, 05(03): 421-434. http://dx.doi.org/10.12677/AAM.2016.53053

参考文献 (References)

  1. 1. Heisenberg, W. (1927) Uber den anschaulichen inhalt der quanten theoretischen Kinematik und Mechanik. Zeitschrift für Physik, 43, 172-198. http://dx.doi.org/10.1007/BF01397280

  2. 2. Heinig, H.P. and Smith, M. (1986) Extensions of the Heisenberg-Weyl Inequality. International Journal of Mathematics and Science, 9, 185-192. http://dx.doi.org/10.1155/S0161171286000212

  3. 3. Selig, K.K. (2002) Uncertainty Principles Revisited. Electronic Transactions on Numerical Analysis, 14, 145-177.

  4. 4. Folland, G.B. and Sitaram, A. (1997) The Uncertainty Principle: A Mathematical Survey. The Journal of Fourier Analysis and Applications, 3, 207-238. http://dx.doi.org/10.1007/BF02649110

  5. 5. Stankovic, L., Alieva, T. and Bastiaans, M.J. (2003) Time-Frequency Signal Analysis Based on the Windowed Fractional Fourier Transform. Signal Processing, 83, 2459-2468. http://dx.doi.org/10.1016/S0165-1684(03)00197-X

  6. 6. Cohen, L. (2000) The uncertainty principles of windowed wave functions. Optics Communications, 179, 221–229. http://dx.doi.org/10.1016/S0030-4018(00)00454-5

  7. 7. Loughlin, P.J. and Cohen, L. (2004) The Uncertainty Principle: Global, Local, or Both? IEEE Transaction on Signal Processing, 52, 1218-1227. http://dx.doi.org/10.1109/TSP.2004.826160

  8. 8. Beckner, W. (1995) Pitt’s Inequality and the Uncertainty Principle. Proceedings of the American Mathematical Society, 123, 1897-1905. http://dx.doi.org/10.1090/s0002-9939-1995-1254832-9

  9. 9. Beckner, W. (1975) Inequalities in Fourier analysis. The Annals of Mathematics, 2nd Ser, 102, 159-182. http://dx.doi.org/10.2307/1970980

  10. 10. Hirschman Jr., I.I. (1957) A Note on Entropy. American Journal of Mathematics, 79, 152-156. http://dx.doi.org/10.2307/2372390

  11. 11. Majerník, V., Majerníková, E. and Shpyrko, S. (2003) Uncertainty Relations Expressed by Shannon-Like Entropies. CEJP, 3, 393-420. http://dx.doi.org/10.2478/bf02475852

  12. 12. Iwo, B.B. (1985) Entropic Uncertainty Relations in Quantum Mechanics. Quantum Probability and Applications II. In: Accardi, L. and von Waldenfels, W., Eds., Lecture Notes in Mathematics 1136, Springer, Berlin, 90.

  13. 13. Maassen, H. (1988) A Discrete Entropic Uncertainty Relation. Quantum Probability and Applications V. Springer- Verlag, New York, 263-266.

  14. 14. Maassen, H. and Uffink, J.B.M. (1983) Generalized Entropic Uncertainty Relations. Physical Review Letters, 60, 1103-1106. http://dx.doi.org/10.1103/PhysRevLett.60.1103

  15. 15. Amir, D., Cover, T.M. and Thomas, J.A. (2001) Information Theoretic Inequalities. IEEE Transactions on Information Theory, 37, 1501-1508.

  16. 16. Iwo, B.B. (2006) Formulation of the Uncertainty Rela-tions in Terms of the Rényi Entropies. Physical Review A, 74, Article ID: 052101.

  17. 17. Iwo, B.B. (2007) Rényi Entropy and the Uncertainty Relations. In, Adenier, G., Fuchs, C.A. and Khrennikov, A.Y., Eds., Foundations of Probability and Physics, American Institute of Physics, Melville, 52-62.

  18. 18. Gill, J. (2005) An Entropy Measure of Uncertainty in Vote Choice. Electoral Studies, 24, 371-392. http://dx.doi.org/10.1016/j.electstud.2004.10.009

  19. 19. Rényi, A. (1960) Some Fundamental Questions of Information Theory. Selected Papers of Alfred Renyi, Vol 2, pp 526-552, Akademia Kiado, Budapest, 1976.

  20. 20. Rényi, A. (1960) On Measures of In-formation and Entropy. Proceedings of the 4th Berkeley Symposium on Mathematics, Statistics and Probability, Berkeley, 20 June-30 July 1960, 547-561.

  21. 21. Shannon, C.E. (1948) A Mathematical Theory of Communication. The Bell System Technical Journal, 27, 379-656. http://dx.doi.org/10.1002/j.1538-7305.1948.tb01338.x

  22. 22. Wódkiewicz, K. (1984) Operational Approach to Phase-Space Measurements in Quantum Mechanics. Physical Review Letters, 52, 1064-1067. http://dx.doi.org/10.1103/PhysRevLett.52.1064

  23. 23. Mustard, D. (1991) Uncertainty Principle Invariant under Fractional Fourier Transform. Journal of the Australian Mathematical Society, 33, 180-191. http://dx.doi.org/10.1017/S0334270000006986

  24. 24. Ozaktas, H.M. and Aytur, O. (1995) Fractional Fourier Domains. Signal Processing, 46, 119-124. http://dx.doi.org/10.1016/0165-1684(95)00076-P

  25. 25. Shinde, S. and Vikram, M.G. (2001) An Uncertainty Principle for Real Signals in the Fractional Fourier Transform Domain. IEEE Transaction on Signal Processing, 49, 2545-2548. http://dx.doi.org/10.1109/78.960402

  26. 26. Stern, A. (2007) Sampling of Compact Signals in Offset Linear Canonical Transform Domains. Signal, Image and Video Processing, 1, 359-367. http://dx.doi.org/10.1007/s11760-007-0029-0

  27. 27. Stern, A. (2008) Uncertainty Principles in Linear Canonical Transform Domains and Some of Their Implications in Optics. Journal of the Optical Society of America A, 25, 647-652. http://dx.doi.org/10.1364/JOSAA.25.000647

  28. 28. Aytur, O. and Ozaktas, H.M. (1995) Non-Orthogonal Domains in Phase Space of Quantum Optics and Their Relation to Fractional Fourier Transform. Optics Communi-cations, 120, 166-170. http://dx.doi.org/10.1016/0030-4018(95)00452-E

  29. 29. Lohmann, A.W. (1994) Relationships between the Radon-Wigner and Fractional Fourier Transfoms. Journal of the Optical Society of America A, 11, 1398-1401. http://dx.doi.org/10.1364/JOSAA.11.001798

  30. 30. Sharma, K.K. and Joshi, S.D. (2008) Uncertainty Principle for Real Signals in the Linear Canonical Transform Domains. IEEE Transaction on Signal Processing, 56, 2677-2683. http://dx.doi.org/10.1109/TSP.2008.917384

  31. 31. Adams, M.D., Kossentini, F. and Ward, R.K. (2002) Generalized S Transform. IEEE Transaction on Signal Processing, 50, 2831-2842. http://dx.doi.org/10.1109/TSP.2002.804085

  32. 32. Schimmel, M. and Gallart, J. (2005) The Inverse S-Transform in Filters with Time-Frequency Localization. IEEE Transaction on Signal Processing, 53, 4417-4422. http://dx.doi.org/10.1109/TSP.2005.857065

  33. 33. Simon, C., Ventosa, S., Schimmel, M. and Heldring, A. (2007) The S-Transform and Its Inverses: Side Effects of Discretizing and Filtering. IEEE Transaction on Signal Processing, 55, 4928-4937. http://dx.doi.org/10.1109/TSP.2007.897893

  34. 34. Chilukuri, M.V. and Dash, P.K. (2004) Multiresolution S-Transform-Based Fuzzy Recognition System for Power Quality Events. IEEE Transactions on Power Delivery, 19, 323-330. http://dx.doi.org/10.1109/TPWRD.2003.820180

  35. 35. Richard, C. (2005) Time-Frequency Analysis of Visual Evoked Potentials Using Chirplet Transform. IEE Electronics Letters, 41, 217-218. http://dx.doi.org/10.1049/el:20056712

  36. 36. Wim, S. (1995) The Lifting Scheme: A New Philosophy in Biorthogonal Wavelet Constructions. SPIE Proceedings of Wavelet Applications in Signal and Image Processing III, 2569, 68-79. http://dx.doi.org/10.1117/12.217619

  37. 37. Emmanuel, J. (2003) Ridgelets: Estimating with Ridge Functions. Annals of Statistics, 31, 1561-1599. http://dx.doi.org/10.1214/aos/1065705119

  38. 38. Donoho, D.L. (2000) Orthonormal Ridgelets and Linear Singularities. SIAM Journal on Mathematical Analysis, 31, 1062-1099. http://dx.doi.org/10.1137/S0036141098344403

  39. 39. Stockwell, R.G., Man-sinha, L. and Lowe, R.P. (1996) Localization of the Complex Spectrum: The S Transform. IEEE Transactions on Signal Processing, 44, 998-1001. http://dx.doi.org/10.1109/78.492555

  40. 40. Assous, S., Humeau, A., Tartas, M., Abraham, P. and L’Huillier, J. (2006) S-Transform Applied to Laser Doppler Flowmetry Reactive Hyperemia Signals. IEEE Transaction on Biomedical Engineering, 53, 1032-1037. http://dx.doi.org/10.1109/TBME.2005.863843

  41. 41. Pinnegar, C.R. and Mansinha, L. (2003) The S-Transform with Windows of Arbitrary and Varying Shape. Geophysics, 68, 381-385. http://dx.doi.org/10.1190/1.1543223

  42. 42. Tao, R., Li, Y. and Wang, Y. (2009) Short-Time Fractional Fourier Transform and Its Applications. IEEE Transaction on Signal Processing, 58, 2568-2580. http://dx.doi.org/10.1109/TSP.2009.2028095

  43. 43. 陶然, 邓兵, 王越. 分数阶Fourier 变换及其应用[M]. 北京: 北京清华大学出版社, 2009.

  44. 44. 冉启文, 谭立英. 分数傅里叶光学导论[M]. 北京: 北京科学出版社, 2004.

  45. 45. 张贤达, 保铮. 非平稳信号分析与处理[M]. 北京: 北京国防工业出版社, 1998.

  46. 46. Pei, S.C., Yeh, M.H. and Luo, T.L. (1999) Fractional Fourier Series Expansion for Finite Signals and Dual Extension to Discrete-Time Fractional Fourier Transform. IEEE Transaction on Signal Processing, 47, 2883-2888. http://dx.doi.org/10.1109/78.790671

  47. 47. Cariolaro, G., Erseghe, T., Kraniauskas, P. and Laurenti, N. (1998) A Unified Framework for the Fractional Fourier Transform. IEEE Transaction on Signal Processing, 46, 3206-3219. http://dx.doi.org/10.1109/78.735297

  48. 48. Barshan, B., Kutay, M.A. and Ozaktas, H.M. (1997) Optimal Filters with Linear Ca-nonical Transformations. Optics Communications, 135, 32-36. http://dx.doi.org/10.1016/S0030-4018(96)00598-6

  49. 49. Ozaktas, H.M., Kutay, M.A. and Zalevsky, Z. (2000) The Fractional Fourier Transform with Applications in Optics and Signal Processing. John Wiley & Sons, New York.

  50. 50. Pei, S.C. and Ding, J.J. (2001) Two-Dimensional Affine Generalized Fractional Fourier Transform. IEEE Transaction on Signal Processing, 49, 878-897. http://dx.doi.org/10.1109/78.912931

  51. 51. Tao, R., Li, B. and Wang, Y. (2007) Spectral Analysis and Reconstruction for Periodic No Uniformly Sampled Signals in Fractional Fourier Domain. IEEE Transactions on Signal Processing, 55, 3541-3547. http://dx.doi.org/10.1109/TSP.2007.893931

  52. 52. Tao, R., Deng, B., Zhang, W. and Wang, Y. (2008) Sampling and Sampling Rate Conversion of Band Limited Signals in the Fractional Fourier Transform Domain. IEEE Transactions on Signal Processing, 56, 158-171. http://dx.doi.org/10.1109/TSP.2007.901666

  53. 53. Xu, G., Wang, X. and Xu, X. (2009) The Logarithmic, Heisenberg’s and Windowed Uncertainty Principles in Fractional Fourier Transform Domains. Signal Processing, 89, 339-343. http://dx.doi.org/10.1016/j.sigpro.2008.09.002

  54. 54. Xu, G., Wang, X. and Xu, X. (2009) The Entropic Uncertainty Principle in Fractional Fourier Transform Domains. Signal Processing, 89, 2692-2697. http://dx.doi.org/10.1016/j.sigpro.2009.05.014

  55. 55. Xu, G., Wang, X. and Xu, X. (2010) Novel Uncertainty Relations in Frac-tional Fourier Transform Domain for Real Signals. Chinese Physics B, 19, 294-302.

  56. 56. Xu, G., Wang, X. and Xu, X. (2009) Three Cases of Uncertainty Principle for Real Signals in Linear Canonical Transform Domain. IET Signal Processing, 3, 85-92. http://dx.doi.org/10.1049/iet-spr:20080019

  57. 57. Zhao, J., Tao, R., Li, Y. and Wang, Y. (2009) Uncertainty Principles for Linear Canonical Transform. IEEE Transactions on Signal Processing, 57, 2856-2858. http://dx.doi.org/10.1109/TSP.2009.2020039

  58. 58. Xu, G., Wang, X. and Xu, X. (2009) Uncertainty Inequalities for Linear Ca-nonical Transform. IET Signal Processing, 3, 392-402. http://dx.doi.org/10.1049/iet-spr.2008.0102

  59. 59. Xu, G., Wang, X. and Xu, X. (2009) New Inequalities and Uncertainty Relations on Linear Canonical Transform Revisit. EURASIP Journal on Advances in Signal Processing, 1-17.

  60. 60. Xia, X.G. (1996) On Bandlimited Signals with Fractional Fourier Transform. IEEE Signal Processing Letter, 3, 72-74. http://dx.doi.org/10.1109/97.481159

  61. 61. Donoho, D.L. and Huo, X. (2001) Uncertainty Principles and Ideal Atomic Decom-position. IEEE Transactions on Information Theory, 47, 2845-2862. http://dx.doi.org/10.1109/18.959265

  62. 62. Calvez, L.C. and Vilbe, P. (1992) On the Uncertainty Principle in Discrete Signals. IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing, 39, 394-395. http://dx.doi.org/10.1109/82.145299

  63. 63. Ishii, R. and Furukawa, K. (1986) The Uncertainty Principle in Discrete Signals. IEEE Transactions on Circuits and Systems, 33, 1032-1034. http://dx.doi.org/10.1109/TCS.1986.1085842

  64. 64. Doroslovacki, M.I. (1998) Product of Second Moments in Time and Fre-quency for Discrete-Time Signals and the Uncertainty Limit. Signal Processing, 67, 59-76. http://dx.doi.org/10.1016/S0165-1684(98)00022-X

  65. 65. Venkatesh, Y.V., Kumar, S. and Vidyasagar, G. (2006) On the Uncer-tainty Inequality as Applied to Discrete Signals. International Journal of Mathematics and Mathematical Sciences, 2006, Article ID: 48185. http://dx.doi.org/10.1155/ijmms/2006/48185

  66. 66. Wilk, G. and Włodarczyk, Z. (2009) Uncertainty Relations in Terms of the Tsallis Entropy. Physical Review A, 79, Article ID: 062108. http://dx.doi.org/10.1103/PhysRevA.79.062108

  67. 67. Bahri, M., Hitzer, E.S.M., Hayashi, A. and Ashino, R. (2008) An Uncertainty Principle for Quaternion Fourier Transform. Computers and Ma-thematics with Applications, 56, 2398-2410. http://dx.doi.org/10.1016/j.camwa.2008.05.032

  68. 68. Stark, H. (1971) An Extension of the Hilbert Transform Product Theorem. Proceedings of the IEEE, 59, 1359-1360. http://dx.doi.org/10.1109/PROC.1971.8420

  69. 69. Havlicek, J.P., Havlicek, J.W., Mamuya, N.D. and Bovik, A.C. (1998) Skewed 2D Hilbert Transforms and Computed AM-FM Models. Proceedings of 1998 International Conference on Image Processing, 1, 602-606. http://dx.doi.org/10.1109/icip.1998.723573

  70. 70. Thomas, B. and Gerald, S. (2001) Hypercomplex Signals: A Novel Extension of the Analytic Signal to the Multidimensional Case. IEEE Transaction on Signal Processing, 49, 2844-2852. http://dx.doi.org/10.1109/78.960432

  71. 71. Sangwine, S.J. and Ell, T.A. (2001) Hypercomplex Fourier Transforms of Color Im-ages. IEEE International Conference on Image Processing, 1, 137-140. http://dx.doi.org/10.1109/icip.2001.958972

  72. 72. Bedrosian, E. (1963) A Product Theorem for Hilbert Transform. Proceedings of the IEEE, 51, 868-869. http://dx.doi.org/10.1109/PROC.1963.2308

  73. 73. 徐冠雷, 王孝通, 徐晓刚. 二象Hilbert变换[J]. 自然科学进展, 2007, 17(8): 1120-1129.

  74. 74. Fu, Y.X. and Li, L.Q. (2006) A Generalized Bedrosian Theorem in Fractional Fourier Domain. 2006 International Conference on Computational Intelligence and Security, 2, 1785-1788. http://dx.doi.org/10.1109/ICCIAS.2006.295369

  75. 75. Xu, G., Wang, X. and Xu, X. (2009) Generalized Hilbert Transform and Its Properties in 2D LCT Domain. Signal Processing, 89, 1395-1402. http://dx.doi.org/10.1016/j.sigpro.2009.01.009

  76. 76. Tao, R., Wang, X. and Wang, Y. (2009) Generalization of Fractional Hilbert Transform. IEEE Signal Processing Letter, 15, 365-368.

  77. 77. Pei, S.C. and Ding, J.J. (2001) Two-Dimensional Affine Generalized Fractional Fourier Transform. IEEE Transaction on Signal Processing, 49, 1638-1655.

  78. 78. Xu, G., Wang, X. and Xu, X. (2009) Improved Bi-Dimensional EMD and Hilbert Spectrum for the Analysis of Textures. Pattern Recognition, 42, 718-734. http://dx.doi.org/10.1016/j.patcog.2008.09.017

  79. 79. Zheng, S., Shi, W., Liu, J. and Tian, J. (2008) Remote Sensing Image Fusion Using Multiscale Mapped LS-SVM. IEEE Transactions on Geoscience and Remote Sensing, 46, 1313-1322. http://dx.doi.org/10.1109/TGRS.2007.912737

  80. 80. Zheng, S., Shi, W., Liu, J. and Tian, J. (2007) Multi Source Image Fusion Method Using Support Value Transform. IEEE Transactions on Image Processing, 16, 1831-1839. http://dx.doi.org/10.1109/TIP.2007.896687

  81. 81. Aanæs, H., Sveinsson, J.R., Nielsen, A., Thomas, B. and Benediktsson, J. (2008) Model-Based Satellite Image Fusion. IEEE Transactions on Geoscience and Remote Sensing, 46, 1336-1346. http://dx.doi.org/10.1109/TGRS.2008.916475

  82. 82. Thomas, C., Ranchin, T., Wald, L. and Chanussot, J. (2008) Synthesis of Multispectral Images to High Spatial Resolution: A Critical Review of Fusion Methods Based on Remote Sensing Physics. IEEE Transactions on Geoscience and Remote Sensing, 46, 1301-1312. http://dx.doi.org/10.1109/TGRS.2007.912448

  83. 83. Liu, Z., Forsyth, D.S., Safizadeh, M.S. and Fahr, A. (2008) A Data-Fusion Scheme for Quantitative Image Analysis by Using Locally Weighted Regression and Dempster-Shafer Theory. IEEE Transactions on Instrumentation and Measurement, 57, 2554-2560. http://dx.doi.org/10.1109/TIM.2008.924933

  84. 84. 覃征, 鲍复民, 等. 数字图象融合[M]. 西安: 西安交通大学出版社, 2004: 7.

  85. 85. 那彦, 焦李成. 基于多分辨分析理论的图象融合方法[M]. 西安: 西安电子科技大学出版社, 2007: 5.

  86. 86. Xu, G., Wang, X. and Xu, X. (2010) On Uncertainty Principle for the Linear Canonical Transform of Complex Signals. IEEE Transactions on Signal Processing, 58, 4916-4918. http://dx.doi.org/10.1109/TSP.2010.2050201

  87. 87. 徐冠雷. 分量分解的信号变换及信号分辨率分析研究[D]: [博士学位论文]. 大连: 海军大连舰艇学院, 2009: 7.

  88. 88. Ding, J.J. and Pei, S.C. (2013) Heisenberg’s Uncertainty Principles for the 2-D Nonseparable Linear Canonical Transforms. Signal Processing, 93, 1027-1043. http://dx.doi.org/10.1016/j.sigpro.2012.11.023

  89. 89. Shi, J., Liu, X. and Zhang, N. (2012) On Uncertainty Principle for Signal Concentrations with Fractional Fourier Transform. Signal Processing, 92, 2830-2836. http://dx.doi.org/10.1016/j.sigpro.2012.04.008

  90. 90. Zhao, J., Tao, R. and Wang, Y. (2010) On Signal Moments and Uncertainty Relations Associated with Linear Canonical Transform. Signal Processing, 90, 2686-2689. http://dx.doi.org/10.1016/j.sigpro.2010.03.017

  91. 91. Xu, G., Wang, X., Zhou, L. and Xu, X. (2013) New Inequalities on Sparse Representation in Pairs of Bases. IET Signal Processing, 7, 674-683. http://dx.doi.org/10.1049/iet-spr.2012.0365

  92. 92. Xu, G., Wang, X., Zhou, L., Shao, L. and Xu, X. (2013) Discrete Entropic Uncertainty Relations Associated with FRFT. Journal of Signal and Information Processing, 4, 120-124. http://dx.doi.org/10.4236/jsip.2013.43B021

  93. 93. Xu, G., Wang, X. and Xu, X. (2014) Generalized Uncertainty Principles Associated with Hilbert Transform. Signal, Image and Video Processing, 8, 279-285. http://dx.doi.org/10.1007/s11760-013-0547-x

  94. 94. Xu, G., Wang, X., Xu, X., Hu, J. and Li, B. (2015) Discrete Inequalities on LCT. Journal of Signal and Information Processing, 6, 146-152. http://dx.doi.org/10.4236/jsip.2015.62014

  95. 95. Xu, G., Wang, X., Xu, X. and Zhou, L. (2016) Entropic Inequalities on Sparse Representation. IET Signal Processing, 10, 413-421. http://dx.doi.org/10.1049/iet-spr.2014.0072

*通讯作者。

期刊菜单