Advances in Applied Mathematics
Vol.06 No.02(2017), Article ID:20040,7
pages
10.12677/AAM.2017.62025
Bifurcation Property of a Class Continuous SIR Model with Vertical and Horizontal Transmission
Mingshan Li1, Yuman Zhang1, Xiaoyu Huang1, Wei Leng2, Xiaopei Li1
1School of Mathematics and Statistics, Lingnan Normal University, Zhanjiang Guangdong
2School of Economics and Statistics, Guangzhou University, Guangzhou Guangdong

Received: Mar. 8th, 2017; accepted: Mar. 27th, 2017; published: Mar. 30th, 2017

ABSTRACT
Bifurcation property of a class SIR model with horizontal and vertical transmission is investigated. Firstly, the type of equilibrium points is determined by discussing its coefficient parameters. Then the transcritical bifurcation and normal form of the model is explored by center manifold theorem. Finally, biological mean of the model is also given.
Keywords:SIR Model, Vertical Transmission, Center Manifold, Transcritical Bifurcation, Normal Form
一类具有水平和垂直传播的连续SIR传染病模型的分岔性质
李明山1,张渝曼1,黄晓玉1,冷薇2,李晓培1
1岭南师范学院数学与统计学院,广东 湛江
2广州大学经济与统计学院,广东 广州
收稿日期:2017年3月8日;录用日期:2017年3月27日;发布日期:2017年3月30日

摘 要
研究一类具有水平和垂直传播的连续SIR传染病模型分岔性质。首先我们讨论了平衡点类型与参数的关系,从而确定平衡点的双曲性和非双曲性,然后通过中心流形研究了模型在无病平衡点的跨临界分岔和正规形,最后给出了模型跨临界分岔的生物学解释。
关键词 :SIR模型,垂直传染,中心流形,跨临界分岔,正规形

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 前言
自从Kermack与McKendrick在1927年文献 [1] 中建立易感(Susceptible)-染病(Infective)-康复(Reco- vered)模型(简称SIR模型)以来,传染病动力学发展迅速,大量的传染病数学模型被应用于分析各种各样的传染病,这些传染病模型大多数是用于研究各种传染病的一般传播规律,对人们研究传染病的传播机制,流行规律和防控理论具有重要的理论意义。近年来在众多学者的探索研究下,涌现出一大批关于传染病模型动力学性质研究的优秀成果 [2] [3] [4] [5] [6] [8] - [16] ,对于连续的SIR模型动力学性质研究中,也涌现出许多优秀的研究成果 [2] - [6] [14] [15] [16] 。对于连续传染病模型而言,不仅仅要研究模型的稳定性,更要研究其分岔性质。因为稳定性仅仅说明了模型所代表的系统受外界干扰时模型解的性质长时间的变化趋势 [7] [10] [14] ,而研究模型分岔性质 [19] 可以得到模型所代表的系统的拓扑结构的变化与模型系数参数的关系,从而得到传染病模型所代表的传染病的相关性质 [11] [12] [13] [15] [16] 。所以研究传染病模型的分岔性质对研究传染病的传播机制与流行规律是非常必要的。
在2008年,Xinzhu Meng和Lansun Chen在文献 [10] 中,根据传统的免疫性连续传染病SIR模型:
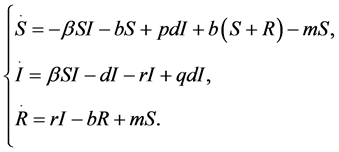 (1)
(1)
建立并研究了一类具有水平和垂直传播的新的免疫性连续传染病SIR模型
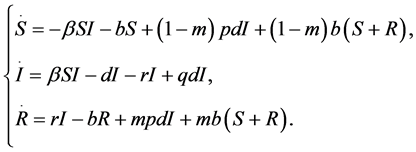 (2)
(2)
无病平衡点处的局部稳定性和地方病平衡点处的全局渐进稳定性,并且得出系统不存在极限环 [10] 。在模型(2)中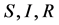 分别代表易感者、染病者、康复者。
分别代表易感者、染病者、康复者。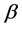 是有效接触率,
是有效接触率, 是出生率,
是出生率, 是死亡率,模型(2)假设在种群中出生率等于死亡率
是死亡率,模型(2)假设在种群中出生率等于死亡率 ,
, 是康复率,
是康复率,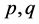 分别代表易感者群体和染病者群体的后代比例,且满足
分别代表易感者群体和染病者群体的后代比例,且满足 ,
, 表示在易感群体中成功免疫的比例,包括成年人。在本文我们首先给出平衡点类型与模型(2)系数参数的关系,进而利用中心流形定理得到了SIR模型跨临界分岔的性质与正规形,最后给出模型在无病平衡点
表示在易感群体中成功免疫的比例,包括成年人。在本文我们首先给出平衡点类型与模型(2)系数参数的关系,进而利用中心流形定理得到了SIR模型跨临界分岔的性质与正规形,最后给出模型在无病平衡点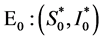 处发生跨临界分岔的生物学解释。
处发生跨临界分岔的生物学解释。
2. 平衡点的类型
在本节,我们在参数空间 ,其中
,其中 上讨论平衡点类型与传染病模型系数参数的关系,确定平衡点的双曲和非双曲性质和平衡点的类型。在文献 [10] 中假设种群数量恒为常数,即
上讨论平衡点类型与传染病模型系数参数的关系,确定平衡点的双曲和非双曲性质和平衡点的类型。在文献 [10] 中假设种群数量恒为常数,即 ,实施尺度变换
,实施尺度变换 ,有
,有
 (3)
(3)
将(3)代入(2)有
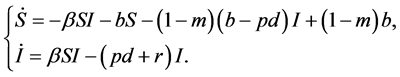 (4)
(4)
系统(4)有两个平衡点,第一个平衡点是没有感染者的群体,称为无病平衡点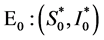 ,其中
,其中 。第二个平衡点是有感染者的群体,称为地方病平衡点
。第二个平衡点是有感染者的群体,称为地方病平衡点 ,其中:
,其中: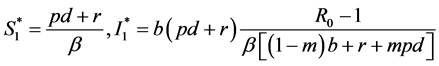 。其中
。其中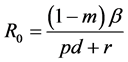 为基本再生率,详见文献 [10] 。从上面实施的尺度变换和传染病模型(4)的生物学意义可知,
为基本再生率,详见文献 [10] 。从上面实施的尺度变换和传染病模型(4)的生物学意义可知, ,故系统(4)的解总是有界的。
,故系统(4)的解总是有界的。
定理2.1无病平衡点 是非双曲的当且仅当
是非双曲的当且仅当 位于直线
位于直线 ,否则无病平衡点
,否则无病平衡点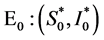 将是如下几种类型;
将是如下几种类型;
i) 当 时,无病平衡点
时,无病平衡点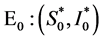 是不稳定的鞍点;
是不稳定的鞍点;
ii) 当 时,无病平衡点
时,无病平衡点 是稳定的结点。
是稳定的结点。
证明 系统(4)在 的雅可比矩阵为
的雅可比矩阵为

其特征值为
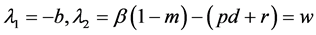
由模型假设可知 ,故
,故 ,当
,当 时,
时, ,所以无病平衡点
,所以无病平衡点 是不稳定的鞍点;当
是不稳定的鞍点;当 时,
时,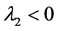 ,所以无病平衡点
,所以无病平衡点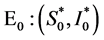 是稳定的结点。
是稳定的结点。
定理2.2 地方病平衡点 不存在非双曲的情形,地方病平衡点
不存在非双曲的情形,地方病平衡点 将是如下几种类型;
将是如下几种类型;
i) 当 时,地方病平衡点
时,地方病平衡点 是稳定焦点;
是稳定焦点;
ii) 当 ,
,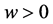 时,地方病平衡点
时,地方病平衡点 是稳定结点;
是稳定结点;
iii) 当 ,
,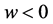 时,地方病平衡点
时,地方病平衡点 是不稳定的鞍点。
是不稳定的鞍点。
证明系统(4)在 处的雅可比矩阵为
处的雅可比矩阵为

其特征方程为

整理得
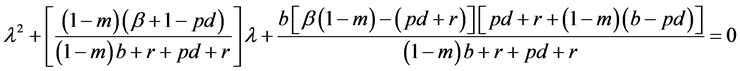
当 时,
时, ,
, ,所以地方病平衡点
,所以地方病平衡点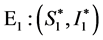 是稳定焦点;当
是稳定焦点;当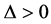 时,记
时,记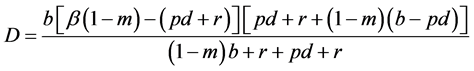 ,并且
,并且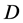 与
与 同号,由韦达定理知
同号,由韦达定理知 ,
,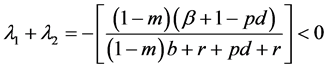 ,故当
,故当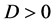 时,即
时,即 ,
, ,所以平衡点
,所以平衡点 是稳定结点,当
是稳定结点,当 时,即
时,即 ,
,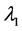 与
与 一正一负,所以地方病平衡点
一正一负,所以地方病平衡点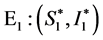 是不稳定的鞍点。当地方病平衡点是非双曲情形时有
是不稳定的鞍点。当地方病平衡点是非双曲情形时有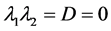 ,
, ,
, ,所以
,所以 与
与 不可能同时为0,故当且仅当
不可能同时为0,故当且仅当 时地方病平衡点
时地方病平衡点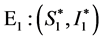 是非双曲的,此时地方病平衡点退化成无病平衡点,两个平衡点重合,此时系统(4)只有一个平衡点,故地方病平衡点
是非双曲的,此时地方病平衡点退化成无病平衡点,两个平衡点重合,此时系统(4)只有一个平衡点,故地方病平衡点 不存在非双曲情形,证毕。
不存在非双曲情形,证毕。
3. 系统(4)的跨临界分岔
在本节,我们将用中心流形定理来研究系统(4)在无病平衡点处 跨临界分岔的性质与正规形,下面的两个引理来自于文献 [18] 。
跨临界分岔的性质与正规形,下面的两个引理来自于文献 [18] 。
引理3.1 [18] 若系统
 (5)
(5)
满足条件:矩阵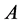 的特征值为0,矩阵
的特征值为0,矩阵 的特征值小于0,且
的特征值小于0,且

则系统(5)存在一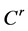 中心流形,在
中心流形,在 局部充分小范围内可表示为
局部充分小范围内可表示为

进一步,限制在中心流形上的系统(5)在 局部充分小范围可以表示为
局部充分小范围可以表示为

引理3.2 [18] 设参数族是 一维系统
一维系统
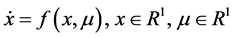 (6)
(6)
满足条件: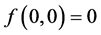 ,
,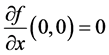 。若
。若

则系统(6)在点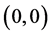 出现跨临界分岔。
出现跨临界分岔。
定理3.1当 ,在平衡点
,在平衡点 处将发生跨临界分岔.具体地讲,对
处将发生跨临界分岔.具体地讲,对 较小的扰动使得
较小的扰动使得 时,系统(4)出现两个平衡点:一个是稳定的无病平衡点
时,系统(4)出现两个平衡点:一个是稳定的无病平衡点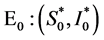 ,另一个是不稳定的负的地方病平衡点
,另一个是不稳定的负的地方病平衡点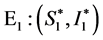 ,它们在
,它们在 时发生粘结合成一点;当
时发生粘结合成一点;当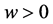 时,系统(4)也出现两个平衡点:一个是不稳定的无病平衡点
时,系统(4)也出现两个平衡点:一个是不稳定的无病平衡点 ,另一个是稳定的正地方病平衡点
,另一个是稳定的正地方病平衡点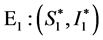 。因此,当
。因此,当 在
在 附近发生微小变化时,系统(4)平衡点的个数发生了改变,并且平衡点
附近发生微小变化时,系统(4)平衡点的个数发生了改变,并且平衡点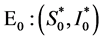 与
与 的稳定性发生了交替,即系统(4)在无病平衡点
的稳定性发生了交替,即系统(4)在无病平衡点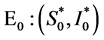 处发生跨临界分岔,且系统(4)在无病平衡点
处发生跨临界分岔,且系统(4)在无病平衡点 处的正规形为
处的正规形为 [17] 。
[17] 。
证明 对于 位于直线
位于直线 ,有
,有 ,为了体现系统(4)在无病平衡点
,为了体现系统(4)在无病平衡点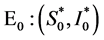 处的跨临界分岔对参数
处的跨临界分岔对参数 的依赖,我们把
的依赖,我们把 写成
写成 ;施行如下坐标变换
;施行如下坐标变换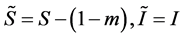 ,易知系统(4)在无病平衡点
,易知系统(4)在无病平衡点 处的雅可比矩阵为,
处的雅可比矩阵为,

及特征值 和
和 对应的特征向量为
对应的特征向量为
 (7)
(7)
记 ,特征值
,特征值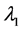 和
和 对应的特征向量可以写成如下形式
对应的特征向量可以写成如下形式
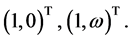 (8)
(8)
由特征向量组(8)我们可以得到如下变换,
 (9)
(9)
由变换(9)可以得到如下系统
 (10)
(10)
把系统(10)写成悬挂式
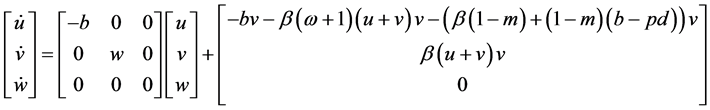 (11)
(11)
由引理3.1可知在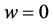 附近可以通过研究中心流形上一参数系统来确定平衡点
附近可以通过研究中心流形上一参数系统来确定平衡点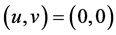 处的稳定性与分岔性质,由引理3.1可知中心流形形式如下;
处的稳定性与分岔性质,由引理3.1可知中心流形形式如下;

由引理3.1假设中心流形有如下形式;
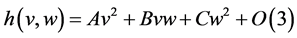 (12)
(12)
由引理3.1知可以通过(13)来计算中心流形(12),其中 表示次数大于或等于3的项;
表示次数大于或等于3的项;
 (13)
(13)
比较系数得
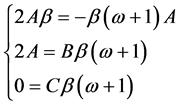
解得 ;故系统(11)在
;故系统(11)在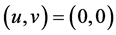 附近中心流形为
附近中心流形为 ,代入系统(11)得
,代入系统(11)得
 (14)
(14)
可以验算如下式子成立
 (15)
(15)
由引理3.2可以知道系统(4)在 发生跨临界分岔,式子(14)表明在
发生跨临界分岔,式子(14)表明在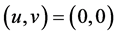 附近所有高阶项
附近所有高阶项 不影响其分岔性质,同时表明在
不影响其分岔性质,同时表明在 附近系统(12)的拓扑结构与(16)的拓扑结构是局部拓扑等价的;
附近系统(12)的拓扑结构与(16)的拓扑结构是局部拓扑等价的;
 (16)
(16)
式子(16)可以看作系统(4)在无病平衡点 处跨临界分岔的正规形。
处跨临界分岔的正规形。
4. 跨临界分岔的生物学解释
由定理3.1可以知道,在 处系统(4)的拓扑结构容易发生质的变化,在
处系统(4)的拓扑结构容易发生质的变化,在 时,地方病平衡点
时,地方病平衡点 是不稳定的且是负的,表明传染病并没有在种群中流行;当
是不稳定的且是负的,表明传染病并没有在种群中流行;当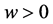 时,地方病平衡点
时,地方病平衡点 是稳定的,即传染病会在种群中稳定流行.所以系统(4)的拓扑结构与传染病的流行与否有着非常紧密的联系,人们可以通过研究传染病模型的拓扑结构并且通过控制传染病模型的有关参数来达到控制流行病的目的,对传染病的传播机理,流行规律的研究与流行病的预防和控制具有重要理论意义。
是稳定的,即传染病会在种群中稳定流行.所以系统(4)的拓扑结构与传染病的流行与否有着非常紧密的联系,人们可以通过研究传染病模型的拓扑结构并且通过控制传染病模型的有关参数来达到控制流行病的目的,对传染病的传播机理,流行规律的研究与流行病的预防和控制具有重要理论意义。
基金项目
国家自然科学基金项目(11561019);广东省创新强校科技重大项目(2014KZDXM065);广东省大学生科技创新重点项目(pdjh2016a0301);广东省大学生科技创新项目(pdjh2017b0314);岭南师范学院攀峰计划项目。
文章引用
李明山,张渝曼,黄晓玉,冷薇,李晓培. 一类具有水平和垂直传播的连续SIR传染病模型的分岔性质
Bifurcation Property of a Class Continuous SIR Model with Vertical and Horizontal Transmission[J]. 应用数学进展, 2017, 06(02): 218-224. http://dx.doi.org/10.12677/AAM.2017.62025
参考文献 (References)
- 1. Kermack, W.O. and McKendrick, A.G. (1927) Contributions to the Mathematical Theory of Epidemics. Proceedings of the Royal Society, 115, 700-721.
- 2. 陈兰荪. 数学生态学模型与研究方法[M]. 北京: 科学出版社, 1988.
- 3. 马知恩, 周义仓, 王稳地, 靳祯. 传染病动力学的数学建模与研究[M]. 北京: 科学出版社, 2004.
- 4. Allen, L.J.S. (1994) Some Discrete-Time SI, SIR and SIS Epidemic Models. Mathematical Biosciences, 124, 83-105. https://doi.org/10.1016/0025-5564(94)90025-6
- 5. Andersonand, R.M. and May, R.M. (1991) Infections Diseases of Humans: Dynamics and Control. Oxford University Press, Oxford.
- 6. Diekmann, O. and Heersterbeek, J.A.P. (2000) Mathematical Epidemiology of Infectious Diseases. Wiley, New York.
- 7. Robinson, R.C. (2004) An Introduction to Dynamical Systems: Continuous and Discrete. Pearson Prentice Hall, Upper Saddle River.
- 8. Anderson, R. and May, R. (1979) Population Biology of Infectious Diseases, Part I. Nature, 280, 361-367.
- 9. Anderson, R. and May, R. (1995) Infections Disease of Humans, Dynamics and Control. Oxford University Press, Oxford.
- 10. Meng, X. and Chen, L. (2008) The Dynamics of a New SIR Epidemic Model Concerning Pulse Vaccination Strategy. Applied Mathematics and Computation, 197, 582-597. https://doi.org/10.1016/j.amc.2007.07.083
- 11. Zhou, X., Li, X. and Wang, W. (2014) Bifurcations for a Deterministic SIR Epidemic Model in Discrete Time. Advances in Difference Equations, 2014, 168.
- 12. Liao, X., Wang, H., Huang, X., Zeng, W. and Zhou, X. (2015) The Dynamic Properties of a Deterministic SIR Epidemic Model in Discrete Time. Applied Mathematics, 6, 1665-1675. https://doi.org/10.4236/am.2015.610148
- 13. Li, M.S., Liu, X.M. and Zhou, X. (2016) The Dynamic Behavior of a Discrete Vertical and Horizontal Transmitted Disease Model under Constant Vaccination. International Journal of Modern Nonlinear Theory and Application, 5, 171-184.
- 14. 杨建雅, 张凤琴. 一类具有垂直传染的SIR传染病模型[J]. 生物数学学报, 2006, 21(3): 341-344.
- 15. 李明山, 刘秀敏, 周效良. 一类离散传染病模型的动力学分析[J]. 广东海洋大学学报, 2017, 37(1): 1-7.
- 16. 商宁宁, 王辉, 胡志兴, 等. 一类具有饱和发生率和饱和治愈率的SIR传染病模型的分支分析[J]. 昆明理工大学学报(自然科学版), 2015, 40(3): 139-148.
- 17. Guckenheimer, J. and Holmes, P. (1983) Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields. Springer, New York.
- 18. Wiggins, S. (1990) Introduction to Applied Nonlinear Dynamical Systems and Chaos. Springer, New York. https://doi.org/10.1007/978-1-4757-4067-7
- 19. Kuznetsov, Y. (2004) Elements of Applied Bifurcation Theory. Springer, New York. https://doi.org/10.1007/978-1-4757-3978-7