Pure Mathematics
Vol.
09
No.
02
(
2019
), Article ID:
29476
,
6
pages
10.12677/PM.2019.92030
Green’s Relations of Semigroup Monotone and k-Preserving Transformations
Yan Sun
School of Mathematics, Guizhou Normal University, Guiyang Guizhou
Received: Mar. 6th, 2019; accepted: Mar. 20th, 2019; published: Mar. 27th, 2019

ABSTRACT
Let
denote a finite set,
is Singular transformation semigroups on it.
and
is Order-preserving and anti-order-preserving transformation semigroups of
. Let
, this paper describes Green’s relations of
.
Keywords:Order Preserving, Transformation Semigroups, Green’s Relations

单调保k变换半群
的Green关系
孙艳
贵州师范大学,数学科学学院,贵州 贵阳

收稿日期:2019年3月6日;录用日期:2019年3月20日;发布日期:2019年3月27日

摘 要
设
是有限集,
是
上的奇异变换半群,
和
是
上的保序变换之集和反保序变换之集,令
,刻画了半群
的Green关系。
关键词 :保序,变换半群,Green关系

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言与准备
众所周知,半群的Green关系研究对于半群代数理论的形成和发展起了极其重要的作用,是研究半群的秩、组合数等的重要内容之一,许多学者对其进行了研究 [1] [2] [3] 。本文考虑
的Green关系,标准定义及未解释符号请参考文献 [4] 。
设
并赋予自然序,
是
上的全变换半群,
是
上的奇异变换半群。设
,若对任意
,有
,称
是保序(反序)的。设
和
分别为
上的保序变换之集和反保序变换之集,则
是
的子半群,称
为
上的保序变换半群。对任意
1 ≤ k ≤ n,令
,
,
则
和
是
的子集。
定义1:设
,令
,
显然,
在变换的合成下构成
的一个子半群,称之为单调保k变换半群。
定义2:设S是半群,
及
,则下列五个关系:
,
,
,
,
统称为半群S上的Green关系。显然,每个D_类是一些L_类与一些R_类的无交并。因此,每个D_类都具有矩阵结构(称为蛋盒图),该矩阵的每一行是一个R_类,每一列是一个L_类,行与列的交叉位置是由R_类与L_类共同决定的H_类,且有限变换半群中
。
2. 主要结果及证明
设
,对任意
,都有
,记作
。
设
,
,记:
;
;
易知,对于
(
表示
中k所在的核类),半群
ORn(k)
的元素
有如下标准表示:
情形1:元素
:
注1:当
时,
是
中最小的核类;当
时,
是
中最大的核类。
情形2:元素
:
注2:当
时,
是
中最小的核类;当
时,
是
中最大的核类。
定理1:设
,则
。
证明:假设
,则存在
,使得
且
,于是
且
,从而
且
。因此
。反之,假设
,
,令
则显然
且
。且
。因此,
。
定理2:设
,则
。
证明:假设
,则存在
,使
,
。任取
,若
,则
,从而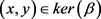 。由
的任意性可得,
。同理可证得,
。因此,
。反之,假设
。不妨设
。由
的任意性可得,
。同理可证得,
。因此,
。反之,假设
。不妨设
其中,
。下面分四种情形讨论:
情形1:设
,则
令
从而存在
,使
。
情形2:设
,则
令
从而存在
,使
。
情形3:设
,则
。
令
从而存在
,使
。
情形4:设
,则
,
,
从而存在
,使
。
综上,
。
定理3:设
,
,
或
。
证明:必要性 先证
。
假设
,则存在
,使得
且
。由定理(1) (2)可得,
,
,从而
。
再证
或
。
假设
,则存在
,使得
且
。则
,
,分以下八种情形:
情形1:设
,则
;
情形2:设
,则
;
情形3:设
,则
;
情形4:设
,则
;
情形5:设
,则
;
情形6:设
,则
;
情形7:设
,则
;
情形8:设
,则
。
充分性:假设
,设
其中,
,
,
。
情形1:
,分四种情形:
子情形1:设
,则
,令
从而存在
,使
,即
。
子情形2:
,则
,令
从而存在
,使
,即
。
子情形3:设
,
,则
,令
从而存在
,使
,即
。
子情形4:设
,
,则
,令
从而存在
,使
,即
。
情形2:
,分四种情形:
子情形1:设
,则
,令
从而存在
,使
,即
。
子情形2:设
,则
,令
从而存在
,使
,即
。
子情形3:设
,
,则
,令
从而存在
,使
,即
。
子情形4:设
,
,则
,令
因此,
且
,从而
。
文章引用
孙 艳. 单调保k变换半群ORn(K)的Green关系
Green’s Relations of Semigroup Monotone and k-Preserving Transformations[J]. 理论数学, 2019, 09(02): 237-242. https://doi.org/10.12677/PM.2019.92030
参考文献
- 1. 陈先军. 保整除变换半群的Green关系及一些组合结果[J]. 贵州师范大学学报(自然科学版), 2010, 28(2): 93-114.
- 2. Deng, L.Z., Zeng, J.W. and Xu, B. (2010) Green’s Relations and Regularity for Semigroups of Transformations That Preserve Double Di-rection Equivalence. Semigroup Forum, 80, 416-425.
- 3. 龙伟锋, 龙伟芳, 高荣海. TE(X)中局部方向保序变换半群的Green 关系和正则性[J]. 贵州师范大学学报(自然科学版), 2009, 27(2): 79-82.
- 4. Howie, J.M. (1995) Fundamentals of Semigroup The-ory. Oxford University Press, Oxford.







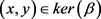 。由
的任意性可得,
。同理可证得,
。因此,
。反之,假设
。不妨设
。由
的任意性可得,
。同理可证得,
。因此,
。反之,假设
。不妨设