Advances in Applied Mathematics
Vol.05 No.01(2016), Article ID:17014,9
pages
10.12677/AAM.2016.51015
Potential Symmetry and Exact Solutions of RLW-Burgers Equation
Chunling Bao, Bilige Sudao*, Yanqing Han
College of Sciences, Inner Mongolia University of Technology, Hohhot Inner Mongolia

Received: Feb. 2nd, 2016; accepted: Feb. 20th, 2016; published: Feb. 26th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
We expanded the classical symmetries of RLW-Burgers equation by calculating the potential symmetries, and we obtained a series of new exact solutions of RLW-Burgers equation. Firstly, we determined the classical symmetries and potential symmetries of RLW-Burgers equation based on differential characteristic set algorithm. Secondly, we constructed the invariant solutions of Burgers equation by using the extended Tanh function method, and these solutions with arbitrary parameters are expressed by the hyperbolic functions, the trigonometric functions and the rational functions, respectively. Finally, new exact solutions for RLW-Burgers equation are obtained by acting Lie transformation group of potential symmetry and the classical symmetry on the invariant solutions. It is important that these solutions can not be obtained from classical symmetries of Burgers equation.
Keywords:Potential Symmetry, Differential Characteristic Set Algorithm, Extended Tanh Function Method, RLW-Burgers Equation, Exact Solutions

RLW-Burgers方程的势对称及其精确解
鲍春玲,苏道毕力格*,韩雁清
内蒙古工业大学理学院,内蒙古 呼和浩特

收稿日期:2016年2月2日;录用日期:2016年2月20日;发布日期:2016年2月26日

摘 要
通过计算RLW-Burgers方程的势对称扩大了其古典对称,并获得了RLW-Burgers方程的一系列新的精确解。首先,基于微分特征列集算法确定了RLW-Burgers方程的古典对称和势对称。其次,利用推广的Tanh函数法构造了RLW-Burgers方程的不变解,这些解分别以含任意参数的双曲函数、三角函数和有理函数表示。最后,分别选择一个势对称和古典对称的Lie变换群,将其作用于RLW-Burgers方程的不变解上获得了新的精确解,重要的是这些解都不能由方程的古典对称得到。
关键词 :势对称,微分特征列集算法,推广的Tanh函数法,RLW-Burgers方程,精确解

1. 引言
Lie对称是公认的普适性最广的方法。近几十年,古典对称的概念得到了很多的推广,人们提出了各种新对称的概念。1988年,Bluman和Cole在Lie群基础上提出了势对称概念[1] 。在诸多新对称中,势对称具有理论简单,算法实现容易,扩展对称性良好的特点。势对称是由微分方程守恒律(守恒形式)引出的扩充方程组来发现原方程的更多相应方程组的古典对称,它可以有效扩大方程对称,并且可以得到方程的更多的精确解。但求偏微分方程的势对称具有很大的局限性,只有少数的偏微分方程具有势对称,具有什么条件的偏微分方程才有势对称也自然而然成为了国内外学者研究的重要课题,并且已有了相关研究 [2] - [10] 。
Lie算法是确定对称的主要方法,该算法的计算过程将涉及到大量、复杂的机械化计算,并且传统的Lie算法中未能考虑未知量的序关系,导致计算机上的无穷循环及工作量大等许多困难。研究发现微分特征列集算法是有效克服Lie算法缺陷的方法之一,该算法主要考虑控制计算过程中符号堆积及易于在机器上实现的问题 [11] 。目前该算法已成功的应用在微分方程的古典对称、非古典对称、高阶对称、近似对称、势对称、守恒律、对称分类、最优系统 [17] 等方面得到了广泛的应用 [4] - [6] [12] - [17] 。本文将基于微分特征列集算法,确定RLW-Burgers方程的古典对称和势对称。
2. RLW-Burgers方程的古典对称和势对称
考虑RLW-Burgers方程
 (1)
(1)
方程(1)是用来描述河道里水波表面的传播问题,其中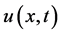 表示距水的表面平衡位置的纵位移,
表示距水的表面平衡位置的纵位移, 表示沿河道流动水的横坐标,
表示沿河道流动水的横坐标,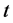 表示所需的时间,
表示所需的时间, 为耗散项,
为耗散项, 为耗散系数,
为耗散系数, 为色散项,
为色散项, 为色散系数,
为色散系数, [18] 。
[18] 。
下面我们基于微分特征列集算法研究RLW-Burgers方程的古典对称和势对称。
2.1. 古典对称分类
假设方程(1)对应的对称向量为
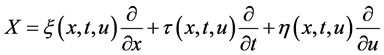 (2)
(2)
其中 ,
, ,
, 是该对称的无穷小生成函数。根据Lie算法,我们可得到方程(1)的对称的确定方程组。但是确定方程组很难人工求解,所以我们可以利用微分特征列集算法 [11] 进行计算得到与确定方程组等价的特征列集对应的方程组,将其求解计算得到以下对称分类结果,见表1。
是该对称的无穷小生成函数。根据Lie算法,我们可得到方程(1)的对称的确定方程组。但是确定方程组很难人工求解,所以我们可以利用微分特征列集算法 [11] 进行计算得到与确定方程组等价的特征列集对应的方程组,将其求解计算得到以下对称分类结果,见表1。
2.2. 势对称
对于RLW-Burgers方程(1),可以将其写成一次守恒形式
 (3)
(3)
为了获得方程(1)的势对称,我们根据此守恒形式引进势变量 ,将方程(3)写成如下等价形式
,将方程(3)写成如下等价形式
 (4)
(4)
假设方程组(4)对应的对称向量为
 (5)
(5)
其中 ,
, ,
, ,
, 是该对称的无穷小生成函数。
是该对称的无穷小生成函数。
定义1. 若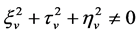 ,即当且仅当无穷小函数
,即当且仅当无穷小函数 ,
, ,
,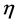 中至少有一个依赖于势变量
中至少有一个依赖于势变量 ,那么
,那么 称为RLW-Burgers方程(1)的势对称。
称为RLW-Burgers方程(1)的势对称。
与上一目的计算类似,很容易得到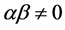 和
和 时方程组(4)的对称,见表2。
时方程组(4)的对称,见表2。
Table 1. The classification of Classical symmetry
表1. 古典对称的对称分类
其中 ,
, 为任意常数。
为任意常数。
Table 2. The classification of potential symmetry
表2. 势对称的对称分类
其中 ,
, 为任意常数。
为任意常数。
下面我们详细讨论 的情况。此时方程组(4)变为
的情况。此时方程组(4)变为
 (6)
(6)
利用Lie算法和微分特征列集算法进行计算得到与确定方程组等价的特征列集对应的如下方程组
 ,
, ,
, ,
,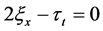 ,
, ,
,
 ,
, ,
,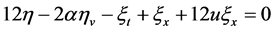 ,
,
 ,
, ,
,
 。
。
对其进行求解得到无穷小生成函数
 ,
, ,
,
 ,
,
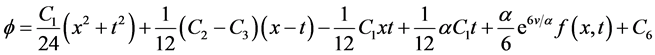 。
。
其中 为任意常数,且函数
为任意常数,且函数 满足关系式:
满足关系式:
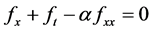 (7)
(7)
根据Lie对称法我们将无穷小函数 中出现的函数
中出现的函数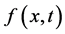 视为对称参数。当选取一个对称参数为1,其余参数为0时,可得到方程组(4)的6个有限维对称和1个无穷维对称,对应的无穷小向量分别为
视为对称参数。当选取一个对称参数为1,其余参数为0时,可得到方程组(4)的6个有限维对称和1个无穷维对称,对应的无穷小向量分别为
 ,
,
 ,
, ,
,
 ,
, ,
, ,
, 。
。
由定义1可知,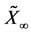 为RLW-Burgers方程的势对称。
为RLW-Burgers方程的势对称。
一般地,我们选择满足关系式(7)的 ,可得到新的势对称。如
,可得到新的势对称。如
1) 取 时,得到势对称
时,得到势对称
 . (8)
. (8)
2) 取 时,得到势对称
时,得到势对称
 . (9)
. (9)
注:只有当 时,RLW-Burgers方程存在势对称。
时,RLW-Burgers方程存在势对称。
3. RLW-Burgers方程的精确解
根据势对称可以构造出微分方程的新不变解,并且这些不变解不能由所研究方程的古典对称求出来的特点,下面我们利用推广的Tanh函数法 [19] 和势对称的单参数Lie变换群构造RLW-Burgers方程的新精确解。
3.1. RLW-Burgers方程的精确行波解
下面我们利用推广的Tanh函数法求解方程(1)在 时的行波解。推广的Tanh函数法是最近提出的求解非线性方程精确解的有效方法之一 [19] 。
时的行波解。推广的Tanh函数法是最近提出的求解非线性方程精确解的有效方法之一 [19] 。
令 ,即在
,即在 ,
, ,
, ,
, 中选取
中选取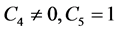 其余
其余 可得到
可得到 ,则
,则 的特征方程为
的特征方程为

得到不变量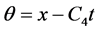 ,其中
,其中 为任意常数。利用特征法可将方程(1)约化为如下的常微分方程
为任意常数。利用特征法可将方程(1)约化为如下的常微分方程
 (10)
(10)
其中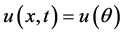 ,
,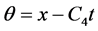 。
。
考虑方程(10)中最高阶导数项 与最高阶非线性项
与最高阶非线性项 的齐次平衡,选择解表达式
的齐次平衡,选择解表达式
 (11)
(11)
其中 ,
, 均为待定常数,而且函数
均为待定常数,而且函数 满足辅助方程
满足辅助方程
 (12)
(12)
其中 ,
,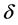 ,
,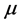 为常数。辅助方程(12)有27种解 [19] ,所以在下文中
为常数。辅助方程(12)有27种解 [19] ,所以在下文中 都将以
都将以 的形式出现,其中
的形式出现,其中 。将表达式(11)代入方程(10)中,并利用方程(12),通过计算可得到方程(1)如下的解
。将表达式(11)代入方程(10)中,并利用方程(12),通过计算可得到方程(1)如下的解
 (13)
(13)
其中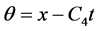 。
。
3.2. 利用Lie变换群作用得到的新精确解
下面将RLW-Burgers方程的势对称及古典对称对应的Lie变换群作用在解(13)上获得新的精确解。我们根据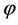 的取值不同选取三角函数解和双曲函数解两类具有代表性的解进行讨论。
的取值不同选取三角函数解和双曲函数解两类具有代表性的解进行讨论。
首先确定对称 和
和 对应的Lie变换群。求解势对称
对应的Lie变换群。求解势对称 对应的初值问题,得到其单参数Lie变换群为
对应的初值问题,得到其单参数Lie变换群为

同理,古典对称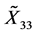 所对应的单参数Lie变换群为
所对应的单参数Lie变换群为

下面将在解(13)的表达式中选择两个具有代表意义的 ,分别在势对称群和古典对称群的作用下得到新的精确解。
,分别在势对称群和古典对称群的作用下得到新的精确解。
1) 三角函数解:
当 ,
, 时,得到
时,得到
 , (14)
, (14)
其中 。将解(14)带入守恒形式(4),得到
。将解(14)带入守恒形式(4),得到
 (15)
(15)
其中 为任意常数。
为任意常数。
下面我们将Lie变换群 作用于解
作用于解 ,
, 即可以得到方程组的另一组解
即可以得到方程组的另一组解
 (16)
(16)
其中 ,
, 的表达式为
的表达式为

将Lie变换群 作用于解
作用于解 ,
, 又可以得到方程组的另一组新解
又可以得到方程组的另一组新解
 (17)
(17)
其中 ,
, 的表达式为
的表达式为
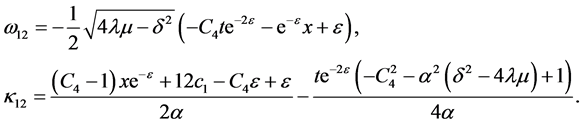
2) 双曲函数解:
当 ,
,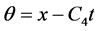 时,得到
时,得到
 , (18)
, (18)
其中 。将解(18)带入守恒形式(4),得到
。将解(18)带入守恒形式(4),得到
 , (19)
, (19)
其中 为任意常数,
为任意常数, 的表达式为
的表达式为

下面我们将Lie变换群 作用于解
作用于解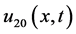 ,
, 即可以得到方程组的另一组解
即可以得到方程组的另一组解
 (20)
(20)
其中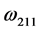 ,
,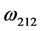 ,
, 的表达式为
的表达式为
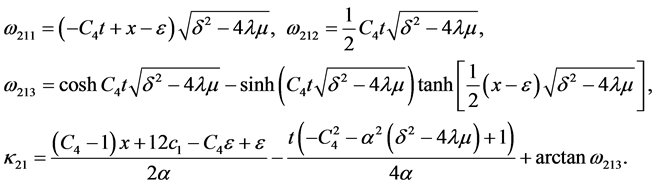
将Lie变换群 作用于解
作用于解 ,
, 又可以得到方程组的另一组新解
又可以得到方程组的另一组新解
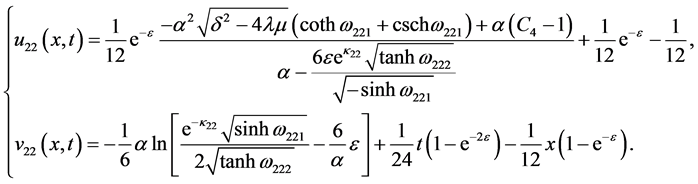 (21)
(21)
其中 ,
, ,
, 的表达式为
的表达式为

如此利用势对称和古典对称对应的Lie变换群作用下去,可以得到更多的精确解。例如我们可确定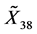 对应的Lie变换群
对应的Lie变换群
我们可将群 作用于精确解构造新的解,因篇幅所限不再一一列出。
作用于精确解构造新的解,因篇幅所限不再一一列出。
4. 本文结论
本文我们基于微分特征列集算法计算了RLW-Burgers方程的古典对称和势对称,并且得到了无穷维对称。为了构造RLW-Burgers方程的新解,利用推广的Tanh函数法构造了RLW-Burgers方程的不变解。并将势对称和古典对称对应的Lie变换群作用于不变解上获得了一系列新的精确解,重要的是这些解(18)~(21)都不能由方程的古典对称得到,这些解丰富了方程原来的精确解 [20] - [22] 。同理我们还可以继续以上过程,即通过对称交替作用得到Lie变换群,并将其作用于RLW-Burgers方程的解得到更多的精确解,这样可以达到通过方程守恒律扩充对称(即势对称)求出更多精确解的目的。
基金项目
本文由国家自然科学基金项目(11571008),内蒙古自治区自然科学基金(2014MS0114),内蒙古自治区研究生科研创新项目(S20151012802)资助。
文章引用
鲍春玲,苏道毕力格,韩雁清. RLW-Burgers方程的势对称及其精确解
Potential Symmetry and Exact Solutions of RLW-Burgers Equation[J]. 应用数学进展, 2016, 05(01): 112-120. http://dx.doi.org/10.12677/AAM.2016.51015
参考文献 (References)
- 1. Bluman, G.W. and Kumei, S. (1989) Symmetries and Differential Equations. Spring-Verlag, New York, Berlin.
- 2. Sophocleous, C. and Wiltshire, R.J. (2006) Linearisation and Potential Symmetries of Certain Systems of Diffusion Equations. Physica A, 370, 329-345. http://dx.doi.org/10.1016/j.physa.2006.03.003
- 3. Qu, C.Z. (2007) Potential Symmetries to System of Nonlinear Diffusion Equation. Journal of Physics A, 40, 1757-1773. http://dx.doi.org/10.1088/1751-8113/40/8/005
- 4. Bluman, G.W. and Chaolu, T. (2005) Local and Nonlocal Symmetries for Nonlinear Telegraph Equation. Journal of Mathematical Physics, 46, 023505. http://dx.doi.org/10.1063/1.1841481
- 5. 特木尔朝鲁, 张志勇. 一类非线性波动方程的势对称分类[J]. 系统科学与数学, 2009, 29(3): 389-411.
- 6. 苏道毕力格, 朝鲁. 用吴方法计算BBM-Burgers方程的势对称及其不变解[J]. 内蒙古大学学报(自然科学版), 2006, 37(4): 366-373.
- 7. 薛春荣. 扩散方程允许的势对称及其精确解. 西安: 西北大学, 2006.
- 8. 康静. 非线性发展方程的势对称及其线性化[D]: [博士学位论文]. 西安: 西北大学, 2008.
- 9. 朱永平, 吉飞宇, 陈晓艳. 广义KdV-Burgers方程的势对称和不变解[J]. 纯粹数学与应用数学, 2013, 29(2): 164- 171.
- 10. 张红霞, 郑丽霞, 杜永胜. Benney方程的势对称和不变解[J]. 动力学与控制学报, 2008, 6(3): 219-222.
- 11. 朝鲁. 微分方程(组)对称向量的吴–微分特征列集算法及其应用. 数学物理学报, 1999, 19(3): 326-332.
- 12. 特木尔朝鲁, 白玉山. 基于吴方法的确定和分类(偏)微分方程古典和非古典对称新算法理论. 中国科学, 2010, 40(4): 1-18.
- 13. 特木尔朝鲁, 额尔敦布和, 郑丽霞. 扩充偏微分方程(组)守恒律和对称的辅助方程方法及微分形式吴方法的应用. 应用数学学报, 2007, 30(5): 910-927.
- 14. Temuer, C.L. and Bai, Y.S. (2009) Differential Characteristic Set Algorithm for the Complete Symmetry Classification of Partial Differential Equations. Applied Mathematics and Mechanics, 30, 595-606. http://dx.doi.org/10.1007/s10483-009-0506-6
- 15. 苏道毕力格, 王晓民, 乌云莫日根. 对称分类在非线性偏微分方程组边值问题中的应用. 物理学报, 2014, 63(4): 040201.
- 16. 苏道毕力格, 王晓民, 鲍春玲. 利用对称方法求解非线性偏微分方程组边值问题的数值解. 应用数学, 2014, 27(4): 708-713.
- 17. Mu, M.R. and Temuer, C.L. (2014) Lie Symmetries, 1-Dimensional Optimal System and Optimal Reductions of (1+2)- Dimensional Nonlinear Schrödinger Equation. Journal of Applied Mathematics and Physics, 2, 603-620. http://dx.doi.org/10.4236/jamp.2014.27067
- 18. Benzalnln, T.B., Bona, J.L. and Mahony, J.J. (1972) Model Eq-uations for Iong Waves in Nonlinear Dlsperslve Systems. Philosophical Transactions of the Royal Society A: Mathe-matical, Physical and Engineering Sciences, 272, 47-78. http://dx.doi.org/10.1098/rsta.1972.0032
- 19. Xie, F.D., Chen, J. and Lü, Z.S. (2005) Using Symbolic Computa-tion to Exactly Solve the Integrable Broer-Kaup Equations in (2+1)-Dimensional Spaces. Communications in Theoretical Physics, 43, 585-590. http://dx.doi.org/10.1088/0253-6102/43/4/003
- 20. 王明亮. Exact Solution for the RLW-Burgers Equation. 应用数学, 1988, 8(1): 51-55.
- 21. 谈骏渝. RLW-Burgers方程的一类解析解. 数学的实践与认识, 2001, 31(5): 545-510.
- 22. 鲍春玲, 苏道毕力格, 盖立涛. RLW-Burgers方程的对称分类及其精确行波解. 内蒙古工业大学学报(自然科学版), 2015, 34(2): 81-86.
*通讯作者。
