Advances in Applied Mathematics
Vol.
09
No.
11
(
2020
), Article ID:
38780
,
6
pages
10.12677/AAM.2020.911230
关于小阶数非交换群的简化幂图
仪钰婷,吴玥雯,安佳薇
西安石油大学理学院,陕西 西安
收稿日期:2020年11月1日;录用日期:2020年11月18日;发布日期:2020年11月25日

摘要
给定一个有限群G,群G上的简化幂图是以G的所有元素为顶点集合的一个简单图,其中两个不同的顶点x和y相邻当且仅当 或 。本文将给出14阶以内的非交换群的简化幂图的结构。此外本文也求了这些群简化幂图的独立数、团数以及彩虹连通数。
关键词
简化幂图,独立数,有限群,团数,彩虹连通数

On the Reduced Power Graphs of Non-Abelian Groups of Small Order
Yuting Yi, Yuewen Wu, Jiawei An
School of Science, Xi'an Shiyou University, Xi'an Shaanxi
Received: Nov. 1st, 2020; accepted: Nov. 18th, 2020; published: Nov. 25th, 2020

ABSTRACT
Given a finite group G, the reduced power graph of G is an undirected graph with vertex set G, and two distinct vertices x and y are adjacent if and only if or . This paper characterizes the structures of the reduced power graphs of non-abelian groups of order at most 14. Moreover, this paper also computes the independence number, clique number, and the rainbow connection number of these graphs.
Keywords:Reduced Power Graph, Independence Number, Finite Group, Clique Number, Rainbow Connection Number

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
本文所涉及的任一图均为一个简单图,即没有重边和自环的无向图。设 是一个图, 的顶点集和边集分别用 和 表示。如果 的一个子集U中任意两个顶点在 中都不能相连,则称U为 的一个独立集。如果向某个独立集中添加任一个在该独立集之外的顶点之后,新构成的集合不再是 的独立集,则原独立集称为是图 的一个极大独立集。具有最大基数的独立集的基数称为图 的独立数。如果 的一个子集C中任意两个顶点在 中都相连,则称C为 的一团。具有最大基数的团的大小称为 的团数。
群上的凯莱图有非常悠久的研究历史,环上的零因子图是近二十年来的一个研究热门课题。研究群或某个代数系统上的图是近些年来的一个新的研究方向。一方面可以根据图的一些性质决定群或代数系统的结构,另一方面,研究这些图在自动化理论的应用。到目前为止,结合图跟环或群然后研究这些图的论文已经不胜枚举,除了前面提到的凯莱图与零因子图以外,如群的共轭类图和素图等,以及环的单位凯莱图等。
本文所涉及的群均为有限群。设G是一个群且 ,g的阶 是最小的正整数n使得 ,其中e是G的单位元。给定一个群G,G上幂图是一个以G为顶点集合的简单图,其中两个元素之间有边的充分必要条件是在G中这两个元素一个可以写成另外一个的幂。在2000年,Kelarev和Quinn [1] 首次引入了群的有向幂图,在2009年,Chakrabarty、Ghosh和Sen [2] 首次引入了群的无向幂图,也简称为群的幂图。近十多年来,学者对幂图的研究非常活跃,看综述文章 [3]。为了减少群幂图中的一些边,Rajkumar和Anitha [4] 介绍了群G的简化幂图 ,该图是以G的所有元素为顶点集合的一个简单图,其中两个不同的元素 相连接的充分必要条件是 或 , 其中 表示由元素x生成的的循环子群。换句话说,群G的简化幂图是从群G的幂图中删除所有满足条件 的边 。因此 是群G的幂图的一个生成子图。在 [4] 中,这两位学者主要研究了群的简化幂图的图理论性质对群结构的影响。
在图理论中,寻找图的具有最大基数的独立集被称为最大独立集问题。众所周知,计算一个图的独立数问题和计算图的团数问题均是NP-困难的。本文将给出14阶以内的非交换群的简化幂图的结构。此外本文也求了这些群简化幂图的独立数、团数以及彩虹连通数。
2. 小阶数的非交换群的简化幂图
本节将给出14阶以内的非交换群的简化幂图的结构。从有限群的分类可知,所有14阶以内的非交换群有 ,其中 分别是8阶的四元数群、4次交错群和12阶双循环群。下面是对14阶以内的非交换群的简化幂图的简短描述。
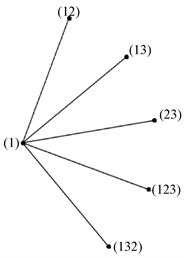
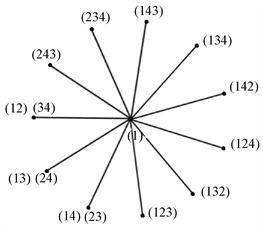
(i) ,其中 ,,,。因此 中每个元素的阶是2,同理(123)和(132)的阶是3。因此可得出 的简化幂图 如图1所示。
图1.
(ii) ,其中 ,,。一个简单的计算表明 ,。我们可以得出:所有的 都只与e相邻,因此可得出 的简化幂图 如图2所示。从图2可以求出 的团数为3,独立数为6。
图2.
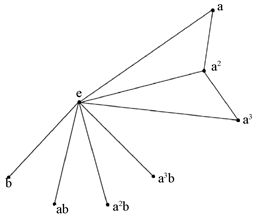
(iii) ,式中 ,,。很容易验证, ,。这些结果表明,除了e和 的阶为2外,每个元素的阶数都是4。 ,, 都是 的循环子群,阶数为4。因此可得出 的简化幂图 如图3所示。从图3可以求出 的团数为4,独立数为6。
(iv) ,其中 ,,。简单计算表明, ,。我们可以得出:所有 只与e相邻,因此可得出 的简化幂图 如图4所示。从图4可以求出 的团数为2,独立数为9。
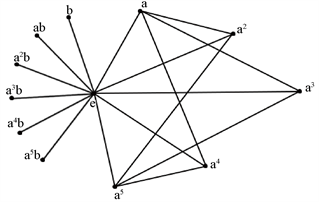
(v) ,其中 ,且 ,,, 都是3阶 的循环子群。所以可得 简化幂图 ,如图5所示。
图3.
图4.
图5.
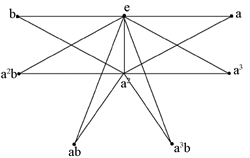
(vi) ,其中 ,,。简单的计算表明, ,,,。因此所有的 都只与e相邻, 与所有的 相邻。所以可得 简化幂图 ,如图6所示。
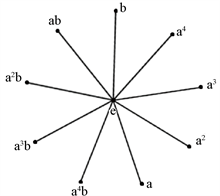
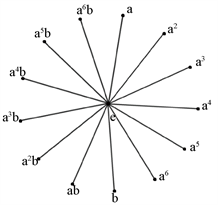
(vii) ,其中 ,,。很容易验证 ,,,,。所以可得 简化幂图 ,如图7所示。
图6.
图7.
(viii) ,其中 ,,。简单计算表明, ,。所以可得 简化幂图 ,如图8所示。
图8.
3. 小阶数的非交换群的简化幂图的一些参数
在图 上定义一个边染色 ,,其中相邻的边可以被染成相同的颜色。如果在该染色 之下,一条路P上的任两条边的颜色都不同,则P称为一条彩虹路。如果对于图 的任两个不同的顶点u和v,均存在一条彩虹路连接这两个顶点,则 称为一个彩虹连通图,并且 称为 的一个彩虹k-染色。使得 彩虹连通的最少的颜色数称为 的彩虹连通数。
本节根据图数、独立数以及彩虹连通数的定义,得到14阶以内的非交换群对应的简化幂图的这些参数值(见表1)。
Table 1. Reduced power graphs corresponding to non-commutative groups of order 14
表1. 14阶以内的非交换群对应的简化幂图
基金项目
本文得到国家级大学生创新创业训练项目(201910705028)的资助。
文章引用
仪钰婷,吴玥雯,安佳薇. 关于小阶数非交换群的简化幂图
On the Reduced Power Graphs of Non-Abelian Groups of Small Order[J]. 应用数学进展, 2020, 09(11): 1990-1995. https://doi.org/10.12677/AAM.2020.911230
参考文献
- 1. Kelarev, A.V. and Quinn, S.J. (2000) A Combinatorial Property and Power Graphs of Groups. Contributions to General Algebra, 12, 229-235.
- 2. Chakrabarty, I., Ghosh, S. and Sen, M.K. (2009) Undirected Power Graphs of Semigroups. Semigroup Forum, 78, 410-426. https://doi.org/10.1007/s00233-008-9132-y
- 3. Abawajy, J., Kelarev, A.V. and Chowdhury, M. (2013) Power Graphs: A Survey. Electronic Journal of Graph Theory and Applications, 1, 125-147. https://doi.org/10.5614/ejgta.2013.1.2.6
- 4. Rajkumar, R. and Anitha, T. (2017) Reduced Power Graph of a Group. Electronic Notes in Discrete Mathematics, 63, 69-76. https://doi.org/10.1016/j.endm.2017.10.063