Computer Science and Application
Vol.
11
No.
04
(
2021
), Article ID:
41744
,
10
pages
10.12677/CSA.2021.114096
结合K-Means与移动最小二乘法的脑部纤维追踪方法
黄丹,战荫伟
广东工业大学计算机学院,广东 广州

收稿日期:2021年3月21日;录用日期:2021年4月15日;发布日期:2021年4月22日

摘要
脑部神经纤维追踪整合单个体素内纤维的方向信息,描绘全局的纤维走向分布,因此单个体素的方向信息决定了纤维追踪结果的准确性和完整性,而传统方法往往直接将体素主特征向量方向作为体素纤维方向,却没有考虑体素张量特性,会产生较大的误差。对此,提出一种结合K-means和移动最小二乘法的纤维追踪方法。首先,根据体素的椭球模型,利用K-means聚类算法将体素聚为3类;接着,用移动最小二乘法拟合非细长椭球状体素的张量信息;最后,采用STT算法对更新后的张量场进行纤维追踪。采用两份数据进行实验结果分析:在真实临床数据中,该算法比STT能追踪到更完整的纤维束;在模拟人脑数据中,该算法能追踪到最多的23束正确纤维束,正确纤维连接比达到45%,错误纤维束相较UKF减少16束,错误纤维连接比降低到28%。
关键词
DTI,移动最小二乘法,扩散加权高斯函数,K-Means,纤维追踪
Brain Fiber Tracking Method Based on K-Means and Moving Least Squares
Dan Huang, Yinwei Zhan
Department Computer Science and Technology, Guangdong University of Technology, Guangzhou Guangdong
Received: Mar. 21st, 2021; accepted: Apr. 15th, 2021; published: Apr. 22nd, 2021

ABSTRACT
Brain nerve fiber tracking refers to the integration of fiber direction information in a single voxel to depict the global fiber direction distribution, so, the direction information of a single voxel determines the accuracy and completeness of the fiber tracking results. Traditional methods often directly use the direction of the main feature vector of the voxel as the direction of the voxel fiber, but do not consider the characteristics of the voxel tensor, which will cause large errors. Therefore, a fiber tracking method combining K-means and moving least square method is proposed. Firstly, according to the ellipsoid model of voxels, the K-means clustering algorithm was used to cluster the voxels into three categories. Then, the tensor information of non-slender ellipsoid voxels was fitted by moving least square method. Finally, STT algorithm is used to track the fiber of the updated tensor field. Two data sets were used to analyze the experimental results. In real clinical data, the algorithm could trace more complete fiber bundles than STT. In simulated human brain data, the algorithm can track the maximum number of correct fiber bundles of 23, the correct fiber connection ratio reached 45%, and the number of wrong fiber bundles decreased by 16 compared to UKF, the wrong fiber connection ratio reduced to 28%.
Keywords:DTI, Moving Least Squares, Diffusion Weighted Gaussian Function, K-Means, Fiber Tracking

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
大脑主要由脑白质、脑灰质和脑脊液组成,其中脑白质是由许多神经纤维束组成的区域。神经纤维束一旦受损,将会导致各种神经系统疾病,因此,神经纤维束的走向和分布一直是脑科学关注的核心问题。扩散张量成像(Diffusion Tensor Imaging, DTI)是用于脑神经纤维追踪的扩散核磁共振成像(Diffusion Magnetic Resonance Imaging, dMRI)技术,能够无创、立体、直观地显示活体神经纤维束,近年来已广泛应用于疾病研究、临床治疗 [1] [2] [3]。
现有脑神经纤维追踪算法主要分为确定性纤维追踪算法和概率性纤维追踪算法。Mori等人 [4] 首先采用张量的主特征向量方向作为体素内纤维方向,进行确定性纤维追踪 (Fiber Assignment by Continuous Tracking, FACT),计算量小,实现简单,但是将纤维定义为一些折线相连,与实际上不符,追踪得到的纤维准确率低。对此,Basser等人 [5] 提出了流线型追踪(Streamline tracking, STT)算法,通过Runge-Kutta积分得到完整光滑的纤维。这两种算法都是直接将体素的主特征向量方向视为纤维方向,在各向异性值大的地方表现较好,在各向异性值小的地方会产生较大的偏差。
概率性纤维追踪算法对体素邻域内的图像信息进行建模,得到纤维方向的概率密度函数,给出所有可能纤维束路径的概率。He [6] 和Lu等人 [7] 采用贝叶斯方法实现张量信息的估计,但需要大量随机采样,耗时长;对此,Kong等人 [8] 通过粒子滤波(Particle Filtering Tractography, PFT)估计扩散张量主特征向量信息;Chinthala [9] 和Chen等人 [10] 利用无损卡尔曼滤波器(Unscented Kalman Filter, UKF)实现纤维追踪;Teillac等人 [11] 通过最小化能量函数估计张量信息。概率性纤维追踪可以减少噪声以及部分容积效应的影响,但是计算量大,效率低,会产生较多的伪纤维,无法为临床医生提供直观的结果。
综上所述,现有确定性纤维追踪算法仅考虑体素自身信息,概率性纤维追踪方法仅考虑邻域体素的影响,导致最终追踪结果会产生较大的误差。因此,本文提出一种既考虑体素局部结构又结合邻域体素信息的确定性纤维追踪方法。先对体素进行聚类,接着,对于非细长状模型体素的张量信息,用移动最小二乘法进行拟合更新,得到新估计的张量信息。最后,在新的张量信息场中进行纤维追踪,得到更加完整准确的脑神经纤维束。实验结果表明此方法可追踪到更加精确完整的纤维束,能够为临床诊断提供辅助分析。
2. 基本原理
2.1. 扩散张量模型
在大脑中,水分子沿着神经纤维的扩散强度远大于垂直于神经纤维的扩散强度,表现为各向异性扩散。为了充分描述每个方向的分子扩散强度以及这些方向之间的相关性,需要由张量参数表示扩散强度,数学上等同于一个3 ´ 3的正定对称矩阵
(1)
设有一个未添加方向梯度脉冲的图像信号S0和N个添加方向梯度脉冲的图像信号 。扩散张量D可通过求解下列方程得到。
(2)
其中gi表示第i个扩散脉冲梯度归一化的方向,b表示扩散敏感因子。
设λ1、λ2、λ3为D的特征值, e1、e2、e3为相应的正交单位特征向量,则
(3)
Westin 等人 [12] 用椭球对扩散张量进行建模,他们提出了三类体素张量模型:细长状、扁平状和圆球形状。当 时,张量模型为细长状见图1(a)。当 时,张量模型为扁平状,见图1(b)。当 时,张量模型为圆球状,见图1(c)。
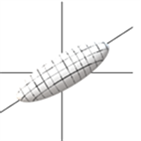 (a) 细长状
(a) 细长状
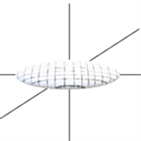 (b) 扁平状
(b) 扁平状
 (c) 圆球状
(c) 圆球状
Figure 1. Three models of diffusion tensors
图1. 扩散张量的三种椭球模型
用CL表示线性扩散的强度,CP表示扁平扩散的强度,CS表示球形扩散的强度,定义为
(4)
显然, 且 。
2.2. K-Means聚类
K-means聚类算法思想简单,效果较好,应用广泛,已用于图像分割、特征学习等方面 [13] [14] [15]。K-means聚类算法通过以下几个步骤实现快速聚类:指定K个聚类中心;计算数据和聚类中心的相似性;通过最小化误差的平方和,迭代更新聚类中心;当误差的平方和不再改变时,聚类结束。
2.3. 移动最小二乘法
2.3.1. 移动最小二乘法原理
移动最小二乘法(Moving Least Squares, MLS) [16] 与最小二乘法最大的不同主要表现在:移动最小二乘法认为体素S处的值f(S)只受S的某个邻域ΩS内体素的影响,邻域ΩS外的体素对f(S)没有影响,这个邻域ΩS称为体素S的影响域。在影响域ΩS上定义一个权函数w设置影响域内体素Si对体素S的影响程度。
取基函数 ,定义体素S的张量拟合函数
其中 为待求系数。
设 ,D(Si)是体素Si处的张量,则体素S处的误差:
(6)
为确定a(S),令E(S)取最小值,则上式对a求导
(7)
令其为零,得
(8)
其中
(9)
(10)
(11)
2.3.2. 权重函数
合适的权重函数可以实现更好的拟合效果。由于纤维追踪是一个连续的过程,邻域体素信息对体素的纤维方向有较大影响,距离越远,影响越小,距离越近,影响越大。因此,采用高斯函数作为权重函数。
各向同性高斯函数形如:
(12)
3. 纤维追踪方法
当体素的张量模型为细长状时,将体素的主特征方向作为纤维方向是可靠的,但是当体素的张量模型为扁平状或者圆球形时,这种方法会产生较大的误差。因此,需要根据张量模型的不同对体素进行聚类,再考虑邻域信息的影响对体素张量信息进行更新。
3.1. 基于扩散特性的K-means聚类
本文基于体素扩散强度参数(CL 、CP、CS)相似性,采用K-means聚类算法将体素聚为3类。具体步骤如下:
步骤1对体素Si设置其标志位Fi = 0,扩散强度系数( 、 、 ), ;设类Qj = Æ,j = 1,2,3;从J中随机选择三个体素作为初始的3个聚类中心{m1、m2、m3};
步骤2对体素Si,计算扩散强度( 、 、 )和聚类中心mj的扩散强度( 、 、 )的相似性:
(13)
若di1 < di2, di3,则令Fi = 1,将Si加入到类Q1中。若di2 < di1, di3,则令Fi = 2,将Si加入到类Q2中。若di3 < di2, di1,则令Fi = 3,将Si加入到类Q3中;di1 = di2 = di3,随机加入一个类中。
步骤3更新聚类中心。重复步骤2~步骤3,直至聚类中心不再变化,此时Fi就是体素Si对应的类别。
3.2. 结合张量模型的自适应各向异性高斯函数
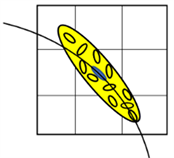
各向同性高斯函数在x、y、z方向设定相同的尺度参数s,且仅考虑邻域体素与体素之间的距离,没有考虑体素的局部结构,如图2(a)所示。然而,在实际纤维追踪过程中,沿着体素主特征向量方向应该分配更高的权重,见图2(b)。因此,宜采用各向异性高斯函数分配权重 [17] [18] [19],在x、y、z方向设定不同的尺度参数sx、sy、sz,即令:
(14)
各向异性高斯函数作为权重函数时,仅能使得x、y、z方向的权重不同,但是实际体素张量的特征向量方向可能是任意的,因此,本文提出一种结合张量模型的自适应各向异性高斯函数,其方向和沿着各个方向的尺度可以随着张量椭球模型变化而变化。
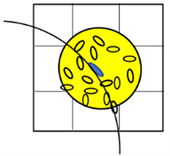 (a) 各向同性高斯模型
(a) 各向同性高斯模型
 (b) 各向异性高斯模型
(b) 各向异性高斯模型
Figure 2. Gaussian function model
图2. 高斯函数模型
为此,对张量D,应根据特征向量e1、e2、e3调整坐标系,根据特征值λ1、λ2、λ3调整尺度,从而为沿着主特征向量方向的体素施加更大的权重因子。设 表示当前体素与邻域体素的偏差向量。定义
(15)
令 ,则上式可表示为:
(16)
即将体素及邻域体素旋转到张量特征向量构成的方向坐标下,并按照特征向量对应的特征值对体素之间距离进行缩放。则上式可表示为:
(17)
因此可构建结合体素张量模型的自适应各向异性高斯函数
(18)
由上述过程可知,上式定义的各向异性高斯函数的方向可随着体素张量模型而调整,并根据特征方向对应的特征值缩放体素与邻域体素的距离,从而为影响域内体素施加合适的权重。
4. 实验
4.1. 算法流程
本文提出的结合K-means和MLS的脑纤维追踪算法KM-STT,具体如图3所示。
步骤1输入DW图像,计算得到DT图像张量数据,并计算DT图像中的FA、CL、CP、CS等值,初始化x,y,z = 0。
步骤2采用基于扩散特性的K-means聚类将体素聚为3类。
步骤3根据聚类结果的不同,选择性的更新张量信息。(a) 选择体素Si (x, y, z);(b) 根据聚类结果判断该体素的扩散张量模型,对于呈扁平状的体素和呈圆球状的体素,选择自适应各向异性高斯函数作为权重函数的MLS对张量进行拟合,更新体素张量;重复(a)~(b)步骤,直至遍历DT图像中的所有体素。
步骤4 在更新后的张量场中,采用STT算法追踪,并可视化纤维追踪结果。
4.2. 实验结果
可以通过对临床数据集进行实验定性的评估纤维追踪结果,但是由于缺少Ground Truth,不能对追踪结果进行定量的比较。使用模拟人脑数据集可以定量的评价追踪结果,但是其无法代替真正的临床数据集。因此本文采用一份临床数据集及一份模拟数据集对追踪结果进行定性定量的评价。
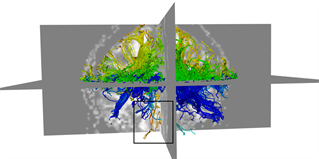
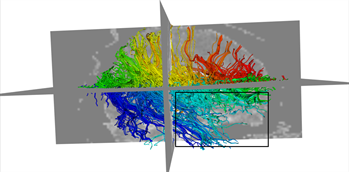
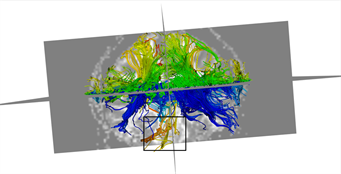
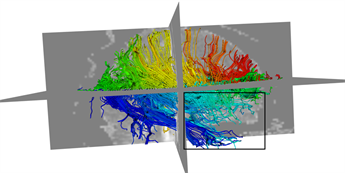
本文采用的临床数据集为头部128 ´ 128 ´ 60的体数据,包括63个施加梯度脉冲信号的DW图像和一个不施加梯度脉冲信号的DW图像,空间分辨率为2 mm ´ 2 mm ´ 1.99 mm,b = 1000 s/mm2。为了更好的比较KM-STT与STT追踪结果,选取感兴趣区域{0 ≤ x < 128, 0 ≤ y < 128, z = 30}进行观察比较。图4所示为STT算法与KM-STT算法追踪效果比较图,其中(a1)~(a2)为STT算法效果图,(b1)~(b2)为KM-STT算法效果图。从局部图可以看出,KM-STT算法的追踪结果相较于STT算法的追踪结果更完整。
本文采用ISMRM2015挑战赛发布的模拟人脑数据进行定量对比实验,该数据集包括33份头部体数据,每份体数据大小为90 ´ 108 ´ 90,空间分辨率为2 mm ´ 2 mm ´ 2 mm,b = 1000 s/mm2。Tractometer [20] [21] 是ISMRM2015挑战赛的独立评估工具,已广泛的应用于该数据集的纤维追踪效果评估 [22] [23]。Tractometer提供的量化指标有:不正确的纤维束数量(Invalid Bundles, IB),正确的纤维束数量(Valid Bundles, VB)表示,错误连接的区域的百分比(Invalid Connection, IC),正确连接的区域的百分比(Valid Connection, VC)。
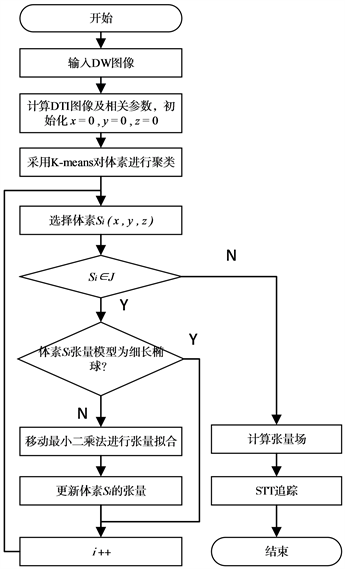
Figure 3. Tensor information update flowchart
图3. 张量信息更新流程图
 (a1)
(a1)
 (b1)
(b1)
 (a2)
(a2)
 (b2)
(b2)
Figure 4. Comparison of tracking effect between STT and KM-STT
图4. STT与KM-STT算法追踪效果比较图
Table 1. Comparison of Tractometer between others and KM-STT
表1. 其他算法与KM-STT算法Tractometer对比表
注:Ground Truth中的VB为25束。
从表1中数据可知,本文算法KM-STT的追踪结果精确度优于STT算法和FACT算法追踪结果。具体表现在:KM-STT相较于其他四种算法可以追踪到更多可用的纤维束(VB);在错误连接比例(IC)方面,PFT + STT追踪结果取得了最小的错误连接比,但是在正确连接(VC)方面,PFT + STT追踪结果的正确连接比最小,KM-STT追踪结果的正确连接比最大,而且在不可用的纤维束中(IB),KM-STT和STT远低于其他三种算法。现有STT、FACT等确定性纤维追踪算法仅考虑体素自身信息,PFT + STT、UKF + STT等概率性纤维追踪方法仅考虑邻域体素的影响,导致最终追踪结果会产生较大的误差。KM-STT作为一种既考虑体素局部结构又结合邻域体素信息的确定性纤维追踪方法,能取得较好的追踪结果。综上所述,通过主观的纤维追踪结果的观察以及客观的追踪数据分析,本文算法KM-STT能提供更加完整,更加精确的纤维追踪结果。
5. 结语
在张量模型为细长状时,采用主特征向量方向作为纤维的行进方向的方法较为可靠,但是当张量模型为圆球形或者扁平状时,这种方法会产生较大的误差。针对此问题,本文提出了一种根据用结合张量值和邻域体素张量特性的纤维追踪方法。由实验效果可以看出,本文提出的算法KM-STT可以追踪出更加完整精确的脑纤维,为临床研究提供视觉效果更加良好的脑纤维追踪结果。在下一步的研究中,可以结合DTI去噪算法减少临床数据中噪声的影响,从而进一步提高在临床数据集中追踪结果的准确率。
基金项目
广东省自然科学基金(No. 2017B010110007)。
文章引用
黄 丹,战荫伟. 结合K-Means与移动最小二乘法的脑部纤维追踪方法
Brain Fiber Tracking Method Based on K-Means and Moving Least Squares[J]. 计算机科学与应用, 2021, 11(04): 928-937. https://doi.org/10.12677/CSA.2021.114096
参考文献
- 1. Yu, Q., Lin, K., Liu, Y. and Li, X. (2020) Clinical Uses of Diffusion Tensor Imaging Fiber Tracking Merged Neuronav-igation with Lesions Adjacent to Corticospinal Tract: A Retrospective Cohort Study. Journal of Korean Neurosurgical Society, 63, 248-260. https://doi.org/10.3340/jkns.2019.0046
- 2. 薛开庆, 张涛. 弥散张量成像技术在癫痫病研究中的应用进展[J]. 西华大学学报(自然科学版), 2019, 38(4): 62-68.
- 3. Baydin, S., Gungor, A., Tanriover, N., Baran, O., Middlebrooks, E.H. and Rhoton Jr., A.L. (2017) Fiber Tracts of the Medial and Inferior Surfaces of the Cere-brum. World Neurosurgery, 98, 34-49. https://doi.org/10.1016/j.wneu.2016.05.016
- 4. Mori, S., Crain, B.J., Chacko, V.P. and Van Zijl, P.C.M. (1999) Three-Dimensional Tracking of Axonal Projections in the Brain by Magnetic Resonance Imaging. Annals of Neurology, 45, 265-269. https://doi.org/10.1002/1531-8249(199902)45:2%3C265::AID-ANA21%3E3.0.CO;2-3
- 5. Basser, P.J., Pajevic, S., Pierpaoli, C., Duda, J. and Aldroubi, A. (2000) In Vivo Fiber Tractography Using DT-MRI Data. Magnetic Reso-nance in Medicine, 44, 625-632. https://doi.org/10.1002/1522-2594(200010)44:4%3C625::AID-MRM17%3E3.0.CO;2-O
- 6. He, W., Chen, C.M., Liu, X. and Shen, H.-W. (2016) A Bayesian Approach for Probabilistic Streamline Computation in Uncertain Flows. 2016 IEEE Pacific Visualization Symposium (PacificVis), Taipei, 19-22 April 2016, 214-218. https://doi.org/10.1109/PACIFICVIS.2016.7465273
- 7. Lu, M. (2015) Brain White Matter Fiber Tracking Re-construction Algorithm Based on Bayesian Model. Journal of Medical Imaging and Health Informatics, 5, 1703-1707. https://doi.org/10.1166/jmihi.2015.1632
- 8. Kong, F., Liu, W., Magnin, I.E. and Zhu, Y. (2016) Cardiac Fiber Tracking Using Adaptive Particle Filtering Based on Tensor Rotation Invariant in MRI. Physics in Medicine and Biology, 61, Article No. 1888. https://doi.org/10.1088/0031-9155/61/5/1888
- 9. Reddy, C.P. and Rathi, Y. (2016) Joint Multi-Fiber NODDI Parameter Estimation and Tractography Using the Unscented Information Filter. Frontiers in Neuroscience, 10, Article No. 166. https://doi.org/10.3389/fnins.2016.00166
- 10. Chen, Z., Tie, Y., Olubiyi, O., Laura, R., Alireza, M., Isaiah, N., et al. (2015) Reconstruction of the Arcuate Fasciculus for Surgical Planning in the Setting of Peritumoral Edema Using Two-Tensor Unscented Kalman Filter Tractography. Neuroimage Clinical, 7, 815-822. https://doi.org/10.1016/j.nicl.2015.03.009
- 11. Teillac, A., Beaujoin, J., Poupon, F., Mangin, J.-F. and Poupon, C. (2017) A Novel Anatomically-Constrained Global Tractography Approach to Monitor Sharp Turns in Gyri. International Conference on Medical Image Computing and Computer-Assisted Intervention, Quebec City, 10-14 September 2017, 532-539. https://doi.org/10.1007/978-3-319-66182-7_61
- 12. Westin, C.F., Maier, S.E., Mamata, H., Nabavi, A., Jolesz, F.A. and Kikinis, R (2002) Processing and Visualization for Diffusion Tensor MRI. Medical Image Analysis, 6, 93-108. https://doi.org/10.1016/S1361-8415(02)00053-1
- 13. MacQueen, J. (1967) Some Methods for Classification and Analysis of Multivariate Observations. Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, Vol. 1, Berkeley, 281-297.
- 14. Hung, P.D., Ngoc, N.D. and Hanh, T.D. (2019) K-Means Clustering Us-ing RA Case Study of Market Segmentation. Proceedings of the 2019 5th International Conference on E-Business and Applications. Bangkok, February 2019, 100-104. https://doi.org/10.1145/3317614.3317626
- 15. Tang, J.L., Zhang, Z.G., Wang, D., Xin, J. and He, L.J. (2018) Research on Weeds Identification Based on K-Means Feature Learning. Soft Computing, 22, 7649-7658. https://doi.org/10.1007/s00500-018-3125-x
- 16. 曾清红, 卢德唐. 基于移动最小二乘法的曲线曲面拟合[J]. 工程图学学报, 2004, 25(1):84-89.
- 17. 付德敏. 各向异性多边滤波在三维点云去噪中的应用研究[D]: [硕士学位论文]. 秦皇岛: 燕山大学, 2017.
- 18. Beitone, C., Balandraud, X., Delpueyo, D. and Grédiac, M. (2017) Heat Source Reconstruction from Noisy Temperature Fields Using a Gradient Anisotropic Diffusion Filter. Infrared Physics & Tech-nology, 80, 27-37. https://doi.org/10.1016/j.infrared.2016.11.003
- 19. Xu, J., Jia, Y., Shi, Z. and Pang, K. (2016) An Improved Ani-sotropic Diffusion Filter with Semi-Adaptive Threshold for Edge Preservation. Signal Processing, 119, 80-91. https://doi.org/10.1016/j.sigpro.2015.07.017
- 20. Côté, M.A., Girard, G., Boré, A., Garyfallidis, E., Houde, J.-C. and Descoteaux, M. (2013) Tractometer: Towards Validation of Tractography Pipelines. Medical Image Analysis, 17, 844-857. https://doi.org/10.1016/j.media.2013.03.009
- 21. Neher, P.F., Descoteaux, M., Houde, J.C., Stieltjes, B. and Maier-Hein, K.H. (2015) Strengths and Weaknesses of State of the Art Fiber Tractography Pipelines—A Compre-hensive In Vivo and Phantom Evaluation Study Using Tractometer. Medical Image Analysis, 26, 287-305. https://doi.org/10.1016/j.media.2015.10.011
- 22. Daducci, A., Dal Palù, A., Lemkaddem, A. and Thiran, J.-P. (2014) COMMIT: Convex Optimization Modeling for Microstructure Informed Tractography. IEEE Transactions on Medical Imaging, 34, 246-257. https://doi.org/10.1109/TMI.2014.2352414
- 23. Maier-Hein, K.H., Neher, P.F., Houde, J.C., Côté, M.-A., Garyfallidis, E., Zhong, J., et al. (2019) Author Correction: The Challenge of Mapping the Human Connectome Based on Diffusion Tractography. Nature Communications, 10, Article No. 5059. https://doi.org/10.1038/s41467-019-12867-2
