Statistics and Application
Vol.07 No.02(2018), Article ID:24673,7
pages
10.12677/SA.2018.72027
N-W Kernel Regression Estimation for Correlation Function of Bivariate Extremes Copula Function
Xiaoyi Jiang, Haomin Zhang, Lifang Liang
College of Science, Guilin University of Technology, Guilin Guangxi

Received: Apr. 3rd, 2018; accepted: Apr. 21st, 2018; published: Apr. 28th, 2018

ABSTRACT
This paper gives an estimate of correlation function for bivariate extremes Copula model using kernel regression method. A N-W kernel regression estimator is constructed and we prove that the estimator is asymptotically unbiased. Based on selection of the optimal bandwidth, we compare the N-W kernel regression estimation and OLS estimation by numerical simulation. The result shows that the N-W kernel regression estimator is more stable than the OLS estimator. So, the N-W kernel regression estimation is a relatively favourable non-parametric method.
Keywords:Extremes Copula Function, Correlation Function, N-W Kernel Regression Estimator
二元极值Copula函数的相关函数的N-W核回归估计
蒋晓艺,张浩敏,梁丽芳
桂林理工大学理学院,广西 桂林

收稿日期:2018年4月3日;录用日期:2018年4月21日;发布日期:2018年4月28日

摘 要
本文利用核回归估计方法对二元极值Copula函数的相关函数进行估计。构建了相关函数的N-W核回归估计。在选择最优带宽的前提下,通过数值模拟对比了N-W核回归估计与OLS估计。数值模拟的结果显示N-W核回归估计在一定情况下较之于OLS估计更具有稳定性,是一种相对较优的相关函数非参数估计方法。
关键词 :极值Copula函数,相关函数,N-W核回归估计

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
1959年Sklar首次提出Copula的概念并证明了任何一个n维联合分布函数都可以用某个Copula函数“连接”n单变量的边际分布函数表达,其中边际分布描述了单个变量的特征,而Copula函数用以刻画边际分布之间的“结构” [1] 。Copula函数本质是把多元随机变量的联合分布函数用各一维边际分布函数连接起来的函数。更进一步,如果给出了一组边际分布和某个Copula函数,那么就可以用该Copula构造一个联合分布。Copula的这种灵活的特征使得它在金融、环境资源管理等领域得到广泛的应用。
Copula函数的优良性质和特殊结构使得其在极端事件统计规律的研究中具有重要作用,极值Copula函数的相关函数作为极值Copula函数的重要推导函数,国外从上个世纪的八十年代开始对相关函数进行估计 [2] 。Csorgo与Revesz率先提出了经典相关函数的非参数Pickands估计 [3] 。Muller和Roeder通过变量替换和顶点限制的方式获得了二元极值Copula相关函数的CFG-估计,并证明了二元CFG-估计为非参数无偏估计 [4] 。2008年,Zhang,Wells和Peng将相关函数的二元CFG-估计推广到了多元,并推导出了多元CFG-估计仍为非参数无偏估计 [5] 。Peter和Nader [6] 通过交叉验证的方法获得了HT-估计。Gordon和Johan [7] 在HT-估计的基础上采用最小二乘法获得了相关函数的OLS-估计。
综合现有的文献可以发现,国内外很多学者关注于极值Copula函数的相关函数的研究。受此启发,本文在OLS-估计和N-W核回归估计模型的基础上构建了二元相关函数的N-W核回归估计并通过数值模拟验证了N-W核回归估计在一定程度上优于OLS-估计 [6] 。
2. 极值Copula函数的相关函数
假设 为二元随机变量,令
为二元随机变量,令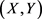 的联合分布函数为H,边缘分布分别为F,G且均为连续函数,则
的联合分布函数为H,边缘分布分别为F,G且均为连续函数,则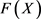 ,
,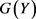 服从
服从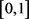 的均匀分布,C为二元极值Copula函数,令
的均匀分布,C为二元极值Copula函数,令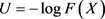 ,
,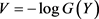 ,任何C都可以有如下表达式 [2] :
,任何C都可以有如下表达式 [2] :
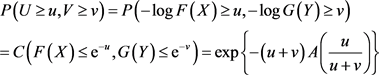 (2.1)
(2.1)
上式中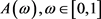 为C的相关函数。函数
为C的相关函数。函数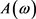 具有如下性质:
具有如下性质:
1)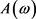 为凸函数;
为凸函数;
2)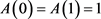 ;
;
3)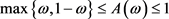 。
。
 为
为 的n个独立样本取
的n个独立样本取 ,
,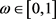 ,
,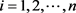 ,由于
,由于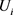 ,
,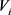 分别为U,V的第i个分量。
分别为U,V的第i个分量。
当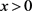 时
时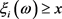 的概率表达式为:
的概率表达式为:
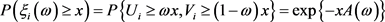 .
.
由此可知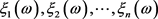 服从均值为
服从均值为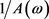 的指数分布。因此,
的指数分布。因此,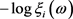 服从位置参数为
服从位置参数为 的Gumbel分布 [7] ,故有
的Gumbel分布 [7] ,故有
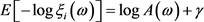 (2.2)
(2.2)
其中g为Euler常数,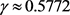 。
。
由(2.2)式得
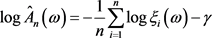 ,
, 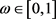 ,
,
有
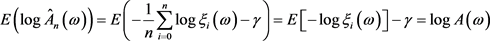
成立,所以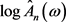 为
为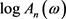 的渐近无偏估计。
的渐近无偏估计。
Kendal’s t系数是一个最具有代表性的相关系数,Kendal’s t系数的定义如下 [8] [9] :
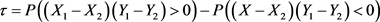
Kendal’s t系数与相关函数的表达式 [4] :
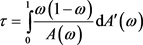
3. N-W核估计
设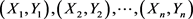 是来自
是来自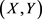 的一个样本,
的一个样本, ,令
,令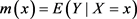 且
且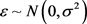 ,则X与Y之间的回归模型为:
,则X与Y之间的回归模型为:
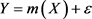 ,
,
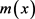 为未知函数,可以通过权函数方法来拟合,对于样本
为未知函数,可以通过权函数方法来拟合,对于样本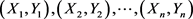 ,权函数估计就是对
,权函数估计就是对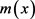 进行估计 [10] 。
进行估计 [10] 。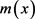 的非参数回归估计量
的非参数回归估计量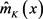 可以表示为:
可以表示为:
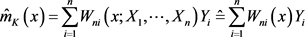
核估计是权函数估计的一种方法,最常见的核估计是Nadaraya和Waston于1964年提出的N-W核权函数回归估计即N-W核估计,N-W核估计得到函数 的核光滑方法即 [11] [12] [13]
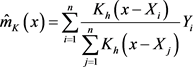 , (3.1)
, (3.1)
其中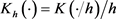 ,
,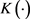 为核函数,h为带宽或窗宽。核函数
为核函数,h为带宽或窗宽。核函数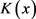 具有以下性质:
具有以下性质:
1)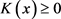 ;
;
2)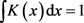 ;
;
3) 。
。
常见的核函数如表1。
依据N-W核回归的定义构建相关函数的核回归的模型:
 ,
, 
由(3.1)可得到相关函数的N-W核估计公式
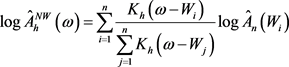 ,
,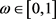 (3.2)
(3.2)
其中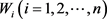 为
为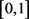 上的随机变量。
上的随机变量。
核估计的结果与带宽h的选择有关所以相关函数的N-W核估计结果同样与带宽h有关。选择的带宽h值越小,核估计的偏差值就会越小,核估计的方差反而越大;反之,选择的带宽h值越大,核估计的偏差值就会越大,核估计的方差反而越小。所以要在核估计的偏差与方差之间做一个权衡,使核估计的均方误差最小。选择带宽主要有直接插入法、经验法则、最小平方交叉验证法和惩罚函数法。本文使用广义交叉验证法的最优带宽公式 [14] :
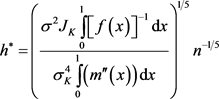
其中 ,
,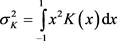 ,
, 为
为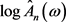 的经验密度函数。
的经验密度函数。
4. 随机模拟
二元极值Copula函数的相关函数的模型 [15] :
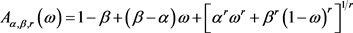 (4.1)
(4.1)
其中 ,
,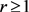 。当
。当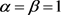 时(4.1)为:
时(4.1)为:
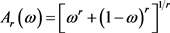 (4.2)
(4.2)
Table 1. Common kernel functions
表1. 常见的核函数
注: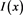 为示性函数。
为示性函数。
模型(4.1)在除去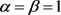 的情况后为非对称模型,本文选择(4.2)模型与估计值进行比较。在(4.2)模型中的r与Kendal’s t系数关系为
的情况后为非对称模型,本文选择(4.2)模型与估计值进行比较。在(4.2)模型中的r与Kendal’s t系数关系为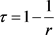 。
。
在本文的模拟过程中相关函数的N-W核回归估计均在最优宽带的前提下选择Gaussian核函数,其中Gaussian核函数的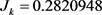 ,
,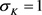 [14] 。表2为样本量分别为50,100和500情况下,随机生成
[14] 。表2为样本量分别为50,100和500情况下,随机生成 的二元随机变量,N-W核估计和OLS估计分别与
的二元随机变量,N-W核估计和OLS估计分别与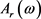 模型的均方误差。表3为样本量分别为250,500和1000情况下,随机生成50%的
模型的均方误差。表3为样本量分别为250,500和1000情况下,随机生成50%的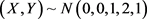 和30%的
和30%的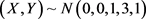 以及20%的
以及20%的 ,的混合分布二元随机变量,N-W核估计和OLS估计分别与
,的混合分布二元随机变量,N-W核估计和OLS估计分别与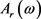 模型的均方误差。
模型的均方误差。
如表2与表3所示的t的值均从0取到0.95,间隔为0.05,相当于r的值从1取到20,但间隔不等。如表2与表3所示在t相同样本量不同的情况下,随着样本量的增加相关函数的N-W核估计和OLS估计与 模型的均方误差几乎均在减小。在如表2所示在t相同样本量相同的情况下,相关函数的N-W核估计与
模型的均方误差几乎均在减小。在如表2所示在t相同样本量相同的情况下,相关函数的N-W核估计与 模型的均方误差均略大于相关函数OLS-估计与
模型的均方误差均略大于相关函数OLS-估计与 模型的均方误差。但是在如表3所示却相反;如表2与表3所示均在样本量相同的情况下,随着r的增加相关函数的N-W核估计与相关函数的OLS-估计的均方误差都逐渐减小再增加;如表2所示相关函数的N-W核估计分别在样本量为50,
模型的均方误差。但是在如表3所示却相反;如表2与表3所示均在样本量相同的情况下,随着r的增加相关函数的N-W核估计与相关函数的OLS-估计的均方误差都逐渐减小再增加;如表2所示相关函数的N-W核估计分别在样本量为50,
Table 2. Mean square error in pure data
表2. 数据纯净情况下的均方误差
Table 3. Mean square error in mixed data
表3. 数据混杂情况下的均方误差
100和500情况下在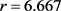 ,
, 和
和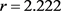 附近处取得最小。相关函数的OLS估计分别在样本量为50,100和500情况下在均在
附近处取得最小。相关函数的OLS估计分别在样本量为50,100和500情况下在均在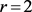 附近处取得最小;如表3所示相关函数的N-W核估计分别在样本量为250,500和1000情况下均在
附近处取得最小;如表3所示相关函数的N-W核估计分别在样本量为250,500和1000情况下均在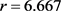 附近处取得最小。相关函数的OLS估计分别在样本量为250,500和1000情况下均在
附近处取得最小。相关函数的OLS估计分别在样本量为250,500和1000情况下均在 和
和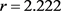 附近处取得最小;在样本量服从
附近处取得最小;在样本量服从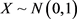 ,
,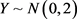 ,
, 的情况下,可知在
的情况下,可知在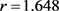 附近处均方误差为最小。有模拟结果可知在分布已知数据纯净的情况下,相关函数的OLS估计效果好,分布未知混杂数据的情况下,相关函数的N-W核估计效果好。
附近处均方误差为最小。有模拟结果可知在分布已知数据纯净的情况下,相关函数的OLS估计效果好,分布未知混杂数据的情况下,相关函数的N-W核估计效果好。
5. 总结
本文在二元极值Copula函数的相关函数OLS估计的基础上,结合具有模型简单,参数少且稳定性高的非参数估计方法N-W核估计,提出了相关函数的N-W核估计,并证明了该估计的无偏性。通过生成服从不相关的二元正态分布的随机变量数值生成N-W核估计与OLS估计模拟相关函数。分别与选定的相关函数的模型进行比较,可以得出N-W核估计的稳定性在分布未知数据混杂的情况下要高于OLS估计。
本文数值分析选择了相关系数单一且样本量较小的情况分析,相关系数的选择和样本量的个数可能会对相关函数的估计会造成影响,在以后的研究中还需进一步的验证方法的适用性。
基金项目
国家自然科学基金项目(71762008)。
文章引用
蒋晓艺,张浩敏,梁丽芳. 二元极值Copula函数的相关函数的N-W核回归估计
N-W Kernel Regression Estimation for Correlation Function of Bivariate Extremes Copula Function[J]. 统计学与应用, 2018, 07(02): 234-240. https://doi.org/10.12677/SA.2018.72027
参考文献
- 1. Sklar, A. (1959) Fonctions de Reparition an Dimensions et Leurs Marges. Publications de l’Intitut de Statistique de I’Universit de Paris, 8, 229-231.
- 2. 吴娟. Copula理论与相关性分析[D]: [博士学位论文]. 武汉: 华中科技大学, 2009.
- 3. Congo, M. and Revesz, P. (1981) Strong Approximation in Probability and Statistics. Academic Press, New York, 7-108.
- 4. Muller, P. and Roeder, K. (1997) A Nonparametric Estimation Procedure for Bivariate Extreme Value Copulas. Biometrika, 84, 567-577.
- 5. Zhang, D., Wells, M.T. and Peng, L. (2008) Nonparametric Estimation of the Dependence Function for a Multi-variate Extreme Value Distribution. Journal of Multivariate Analysis, 99, 577-588.
- 6. Hall, P. and Tajvidi, N. (2000) Distri-bution and Dependence-Function Estimation for Bivariate Extreme-Value Distributions. Bernoulli, 6, 835-844.
- 7. Gudendorf, G. and Segers, J. (2011) Nonparametric Estimation of an Extreme-Value Copula in Arbitrary Dimensions. Journal of Multivariate Analysis, 102, 37-47.
- 8. Fredricks, G.A. and Nelsen, R.B. (2007) On the Relationship between Spearman’s Rho and Kendall’s Tau for Pairs of Continuous Random Variables. Journal of Statistical Planning & Inference, 137, 2143-2150.
- 9. Niewiadomska-Bugaj, M. and Kowalczyk, T. (2005) On Grade Transformation and Its Implications for Copulas. Brazilian Journal of Probability & Statistics, 19, 125-137.
- 10. 吴喜之, 王兆军. 非参数统计方法[M]. 北京: 高等教育出版社, 1996: 274-277.
- 11. Hardle, W. (1990) Applied Nonparametric Regression: References. Cambridge University Press, 225-226.
- 12. Hart, J.D. (1997) Nonparametric Smoothing and Lack-of-Fit Tests. Springer, 6-176.
- 13. 陈希孺, 方兆本, 李国英. 非参数统计[M]. 上海: 上海科学技术出版社, 1989: 361-367.
- 14. 李艳娟. 核估计量与窗宽选择[J]. 辽宁工程技术大学学报, 2006, 25(3): 478-480.
- 15. Tawn, J. (1988) Bivariate Extreme Value Theory: Models and Estimation. Biometrika, 75, 397-451.
