Advances in Applied Mathematics
Vol.05 No.03(2016), Article ID:18445,5
pages
10.12677/AAM.2016.53056
Study on Exact Solutions of (2 + 1)-Dimensional K-P Equation
Huifang Wei
School of Mathematics and Statistics, Yunnan University of Finance and Economics, Kunming Yunnan

Received: Aug. 17th, 2016; accepted: Aug. 27th, 2016; published: Aug. 30th, 2016
Copyright © 2016 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, we mainly use the dynamical systems method to solve the (2 + 1) dimensional KP equation. By introducing the traveling wave transformation, the original (2 + 1) dimensional KP equation is transformed into ordinary differential equations. After that, we analyze the singular points, the corresponding bifurcation and phase diagram of the system. Finally, the solution of the original equation is obtained by using the Maple software, including the sharp wave solutions and periodic wave solutions.
Keywords:Dynamical Systems, Sharp Wave Solution, K-P Equation

(2 + 1)-维K-P方程精确解的研究
卫慧芳
云南财经大学统计与数学学院,昆明,云南

收稿日期:2016年8月17日;录用日期:2016年8月27日;发布日期:2016年8月30日

摘 要
本文主要采用动力系统方法对(2 + 1)维Kadmotsev and Petviashvili (KP)方程进行研究,通过引入行波变换,将原(2 + 1)维K-P方程转化为常微分方程组。之后,对这个方程组的奇点,对应的分支和相图进行分析。最后,运用Maple软件求得用原方程的解,包括尖波解,周期波解。
关键词 :动力系统,孤立波解,K-P方程

1. 引言
非线性偏微分方程 [1] 是现代数学的一个重要分支。近年来,许多研究者在实践探索中得到了很多可行的求解非线性偏微分方程精确解的方法。例如:展开法 [2] ,tanh函数法 [3] ,F展开法 [4] ,Darboux变换法 [5] ,齐次平衡法 [6] 等。而用动力系统方法 [7] 来求解非线性偏微分方程正在引起研究者们的高度重视。
李继彬教授在用动力系统方法求解偏微分方程方面的研究颇有建树,对我们在该方面的研究提供了很多的经典论述。比如,他用此方法结合maple软件对KDV方程,非线性对流-扩散型方程,广义C-H方程以及广义非线性薛定谔方程等进行了求解,是非常有影响力的。
本文所研究的方程为:
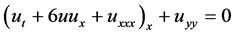 (1)
(1)
在文献 [8] [9] 中,均采用不同的方法,对K-P方程进行了研究,得到了N-孤子解,周期孤波解等。而行波法中的动力系统方法为其他研究中所没有使用到的。在本文中,我们将采用动力系统方法,对方程(1)进行求解,充分的扩充该方程的解空间。
2. 偏微化常微
在这一部分,我们先引入行波变换,将原偏微分方法(1)化为常微分方法组,引入的变换如下:
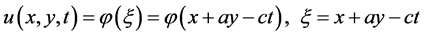 (2)
(2)
其中,a为任意实常数,c为波速。由(2)式可算得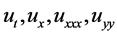 ,带入(1)式有:
,带入(1)式有:
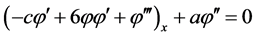 (3)
(3)
对(3)式积分两次,为简化计算,取积分常数为0,可得:
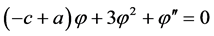 (4)
(4)
(4)式等价于如下的二维系统:
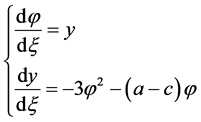 (5)
(5)
对应的首次积分,即它的哈密尔顿量为:
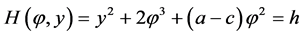 (6)
(6)
到这一步,我们已经把原偏微分方法(1)化为常微分方法组(5),基本的铺垫工作已经完成。
3. 分析系统(5)的分支和相图
接下来,我们将对系统(5)的分支和相图进行分析。对于(5)式,令 且
且 。显然,
。显然,
存在两个奇点: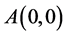 ,
,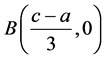 ,且对应的哈密尔顿量为
,且对应的哈密尔顿量为
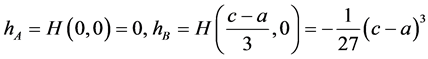 ,对于奇点的类型,我们还需要通过系统(5)对应的雅克
,对于奇点的类型,我们还需要通过系统(5)对应的雅克
比行列式来判定,如(7)式:
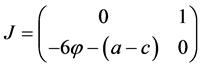 (7)
(7)
对应的特征值: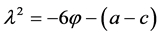 ,在A点,
,在A点, ;在B点,
;在B点,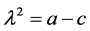 ;根据特征值同号为结点,异号为鞍点,纯虚数为中心的概念易见:
;根据特征值同号为结点,异号为鞍点,纯虚数为中心的概念易见:
1) 当 时,A为鞍点,B为中心,见图1;
时,A为鞍点,B为中心,见图1;
2) 当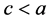 时,A为中心,B为鞍点,见图2;
时,A为中心,B为鞍点,见图2;
3) 当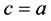 时,仅为一个奇点
时,仅为一个奇点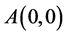 ,见图3。
,见图3。

Figure 1. c > a
图1. c > a
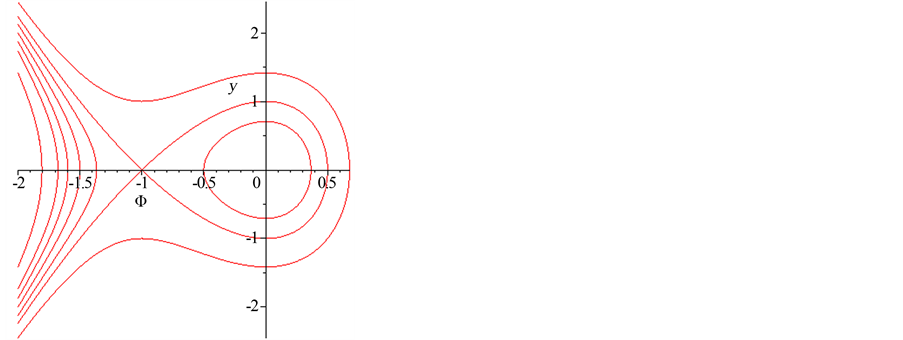
Figure 2. c < a
图2. c < a
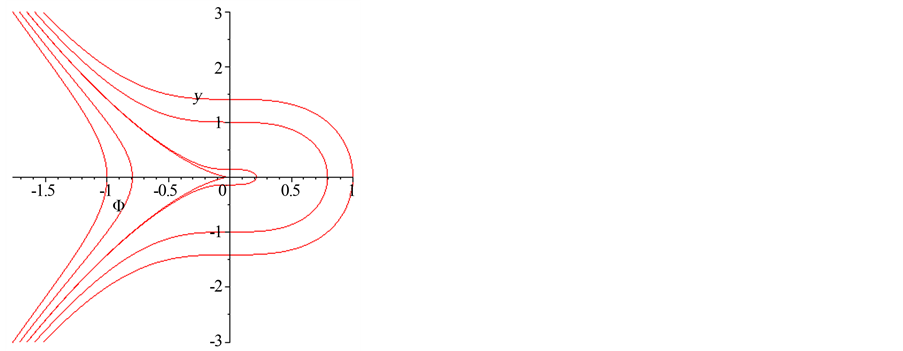
Figure 3. c = a
图3. c = a
根据上面划分的参数空间,可以画出各个参数空间下对应的相图,便于分析其分支及奇点附近轨线的拓扑结构。
图1中,当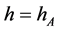 时,为同宿轨道,对应孤立波解;当
时,为同宿轨道,对应孤立波解;当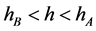 时,为周期轨道,对应周期波解;图2中,当
时,为周期轨道,对应周期波解;图2中,当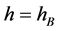 时,为同宿轨道,对应孤立波解;当
时,为同宿轨道,对应孤立波解;当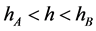 时,为周期轨道,对应周期波解;图3中,均为无界边解,不做研究。
时,为周期轨道,对应周期波解;图3中,均为无界边解,不做研究。
4. 方程的求解
这部分,也就是本文最重要的部分,求解方程(1)的解。从哈密顿量系统入手,有:
 (8)
(8)
借助Maple对上式两边积分,即可得到方程的精确解。具体情况如下:
1) 当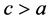 ,
,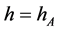 时,带入(8)后,借助Maple两边积分一次,可得孤立波解
时,带入(8)后,借助Maple两边积分一次,可得孤立波解
 (9)
(9)
2) 当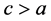 ,
,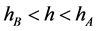 时,带入(8)后,借助Maple两边积分一次,可得周期波解
时,带入(8)后,借助Maple两边积分一次,可得周期波解
 (10)
(10)
其中,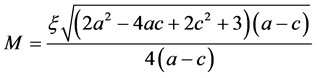 。
。
3) 当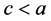 ,
,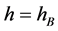 时,带入(8)后,借助Maple两边积分一次,可得孤立波解
时,带入(8)后,借助Maple两边积分一次,可得孤立波解
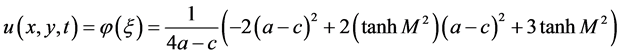 (11)
(11)
其中, 。
。
4) 当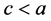 ,
,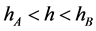 时,带入(8)后,借助Maple两边积分一次,可得周期波解为
时,带入(8)后,借助Maple两边积分一次,可得周期波解为
 (12)
(12)
5. 结论
本文用动力系统方法求解(2 + 1)维K-P方程,求得用三角函数表示的方程的新解,分别为孤立尖波解和周期波解,式子(9)~(12),拓展了该方程的解空间。可见,用动力系统方法求解偏微分方程与其他方法相比,是更简单,有效的。
文章引用
卫慧芳. (2 + 1)-维K-P方程精确解的研究
Study on Exact Solutions of (2 + 1)-Dimensional K-P Equation[J]. 应用数学进展, 2016, 05(03): 450-454. http://dx.doi.org/10.12677/AAM.2016.53056
参考文献 (References)
- 1. 唐晓芬. 非线性偏微分方程的几类求解方法[D]: [硕士学位论文]. 镇江: 江苏大学, 2009.
- 2. Bilige, S. and Chaolu, T. (2011) A Generalized (G’/G)-Expansion Method and Its Applications. Journal of Mongolia University Natural Science Edition, 1, 15-37.
- 3. 徐振民. 推广的Tanh-函数法及其应用[J]. 广西民族大学学报(自然科学版), 2009, 3(15): 54-56.
- 4. 刘涛立. F-展开法研究[D]: [硕士学位论文]. 兰州: 兰州大学, 2004.
- 5. 闵迪. 非线性发展方程的求解与达布变换[D]: [硕士学位论文]. 大连: 辽宁师范大学, 2010.
- 6. 杨攀攀. 齐次平衡法和非线性偏微分方程的孤立波解[D]: [硕士学位论文]. 南京: 南京理工大学, 2008.
- 7. Li, J.B. (2013) Singular Nonlinear Traveling Wave Equations: Bifurcations and Exact Solutions. Science Press, Beijing, 1-70.
- 8. 杨翠平. (3+1)维KP方程的N-孤子解[J]. 湖北广播电视大学学报, 2010, 12(30): 160-162.
- 9. 傅海明, 戴正德. (3+1)维K-P方程的周期波解[J]. 山西大学学报(自然科学报), 2010, 33(1): 4-7.