Advances in Applied Mathematics
Vol.
08
No.
12
(
2019
), Article ID:
33517
,
10
pages
10.12677/AAM.2019.812234
Inequalities for Dual Orlicz Mixed Affine Quermassintegrals
Guojun Deng, Yan Gou
Lanzhou No.9 Middle School, Lanzhou Gansu

Received: 23rd, 2019; accepted: Dec. 11th, 2019; published: Dec. 18th, 2019

ABSTRACT
This paper generalizes the notion of dual affine quermassintegrals in the classical Brunn-Minkowski theory and its inequalities to Orlicz space. Concept of dual Orlicz mixed affine quermassintegrals is introduced in this paper, and the Orlicz-Minkowski inequality and the Orlicz-Brunn-Minkowski inequality are established for this new dual Orlicz mixed affine quermassintegrals.
Keywords:Star Bodies, Orlicz Space, Dual Orlicz Mixed Affine Quermassintegrals, Orlicz-Minkowski Inequality, Orlicz-Brunn-Minkowski Inequality

对偶Orlicz混合仿射均质积分的不等式
邓国军,缑艳
兰州市第九中学,甘肃 兰州

收稿日期:2019年11月23日;录用日期:2019年12月11日;发布日期:2019年12月18日

摘 要
本文将经典Brunn-Minkowski理论中对偶仿射均质积分的概念及相关不等式推广到Orlicz空间,提出了对偶Orlicz混合仿射均质积分的概念,建立了对偶Orlicz混合仿射均质积分的Orlicz-Minkowski不等式和Orlicz-Brunn-Minkowski不等式。
关键词 :星体,Orlicz空间,对偶Orlicz混合仿射均质积分,Orlicz-Minkowski不等式,Orlicz-Brunn-Minkowski不等式

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言和主要结果
早在19世纪末20世纪初,Brunn-Minkowski理论开始逐渐进入人们的视野。从1962年开始,Brunn-Minkowski理论逐渐进入 Brunn-Minkowski理论阶段(见 [1] ),在经过Lutwak (见 [2] [3] )等的基础性工作之后, Brunn-Minkowski理论得到迅速的发展(见 [4] - [10] )。最近,在Lutwak Yang和Zhang等人的开创性研究(见 [11] [12] )和近期的一系列探究性工作(见 [13] [14] [15] )的推动下,凸体的经典Brunn-Minkowski理论(见 [16] [17] [18] [19] ) (包括 Brunn-Minkowski理论(见 [20] ))已被推广到Orlicz-Brunn-Minkowski理论之中。
设 和B分别表示n维欧式空间 中的单位球面和标准单位球,用 表示 中所有凸体(非空内点的紧凸集)构成的集合, , 分别表示 中以原点为内点和关于原点对称的所有凸体构成的集合。 表示k维体积,且记 。在 中,一个紧的星形(关于原点) K的径向函数 被定义为:对 ,。当 是一个正的连续函数时,称K是一个星体(关于原点)。设 为 中所有星体(支撑上有连续径向函数的关于原点的星形集)构成的集合,用 表示 中以原点为内点的所有星体构成的集合。如果 且 与 无关,则称K和L互为膨胀。显然,当 时,
当且仅当 (1.1)
若 ,就有
(1.2)
一般地,根据径向函数的定义可得:若 ,则K的象 的径向函数为(见 [16] [21] )
(1.3)
其中 表示一般的非奇异线性变换群, 为T的逆变换。
关于凸体仿射均质积分的概念,Lutwak (见 [22] )已给出了明确的定义:如果 ,,,那么当 时,凸体K的仿射均质积分被定义为
其中 和 分别表示 中i维线性子空间的Grassman流形(且 ), 上规范Haar测度和K在i维子空间 上正交投影的i维体积。
在文献 [23] 中,Lutwak进一步给出对偶仿射均质积分的定义:如果 ,,,那么对于 ,星体K的对偶仿射均质积分被定义为
(1.4)
其中 表示K与i维子空间 交的i维体积。
随后,袁俊(见 [9] )给出混合p次对偶仿射均质积分的概念:如果 ,,那么对于 ,混合p次对偶仿射均质积分被定义为
(1.5)
其中 。当 时, 可记为对偶混合仿射均质积分 。当 时,就有 ,。
在此基础上,袁俊(见 [9] )给出了如下两个重要的不等式:
定理A:如果 ,且 ,那么当 时,
(1.6)
等号成立当且仅当K是L的膨胀。
定理B:如果 ,且 ,那么
(1.7)
等号成立当且仅当K是L的膨胀。
设 是所有严格增的凹函数 所构成的集合,且使得 和 。
文献 [14] 和 [15] 各自独立地给出了如下的对偶Orlicz混合体积 的公式:对于 ,,对偶Orlicz混合体积 为
(1.8)
其中S是 上的Lebesgue测度。当 时,对于 ,对偶Orlic混合体积 变为p次对偶混合体积,即
本文提出了如下对偶Orlicz混合仿射均质积分的定义,从而推广了混合p次对偶仿射均质积分的概念。在此基础上,讨论了对偶Orlicz混合仿射均质积分的一些性质,建立了对偶Orlicz混合仿射均质积分的Orlicz-Minkowski不等式和Orlicz-Brunn-Minkowski不等式。
首先,提出对偶Orlicz混合仿射均质积分的定义。
定义1.1:设 ,。如果 ,那么对每一个 ,对偶Orlicz混合仿射均质积分被定义为
(1.9)
其中 表示 和 的i维对偶Orlicz混合体积。
当 时,对偶Orlicz混合仿射均质积分(1.9)变为袁俊(见 [9] )的混合p次偶仿射均质积分(1.5)。
其次,获得了对偶Orlicz混合仿射均质积分的Orlicz-Minkowski不等式。
定理1.2:如果 ,,那么对每一个 ,
(1.10)
等号成立当且仅当K和L互为膨胀。
最后,利用定理1.2,建立了可推出对偶Orlicz混合仿射均质积分的Orlicz-Brunn-Minkowski不等式。
定理1.3:如果 , 且 。那么对每一个 ,
(1.11)
等号成立当且仅当K和L互为膨胀(径向Orlicz线性组合 的定义请见第二节(2.2))。
2. 预备知识及引理
如果 ,,那么径向Minkowski线性组合, ,被定义为
当 , 时,
由此,易得
对于 ,在 上定义径向Hausdorff度量为
若当 ,。则星体列 收敛于K。这意味着当且仅当 一致收敛于 时,序列 收敛于K。
一个紧的星形K的n维体积的极坐标公式是
(2.1)
最近,Gardner(见 [14] )等人给出了径向Orlicz线性组合 的定义:设 ,如果 ,,那么对任意 ,径向Orlicz线性组合 被定义为
(2.2)
并有 ,由(2.2)可以知道, 在 上是Borel可测的。
等价地,设 ,如果 ,,那么对于任意 ,径向Orlicz线性组合 亦可定义为
(2.3)
那么,当 时, 。
引理2.1:设 ,,如果 ,那么对于 ,
证明:对于任意 ,由等式(1.3)和径向Orlicz线性组合的定义(2.2),得
引理2.2:设 ,,且 ,如果 ,那么对于 ,
证明:设 是任意固定的,记 。对于 和 ,有 。由此,利用 的定义,对 ,可得
另一个方面,利用 上 的定义,可得
因此,在 中, 和 是同一个星体。
Gardner (见 [14] )等证明了如下对偶Orlicz混合体积的对偶Orlicz-Minkowski不等式。
引理2.3:如果 ,,那么
等号成立当且仅当K和L互为膨胀。
3. 主要结果的证明
首先获得了对偶Orlicz混合仿射均质积分的一些基本性质。
性质3.1:如果 ,,那么
1) 。
2) 。
3) 如果 ,那么 。
4) 当 时, 。
我们只给出性质(4)的证明。
证明:设
,记
。如果
,则对于
,,有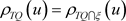 。当
。当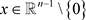 时,记
时,记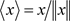 ,利用对偶Orlicz混合体积(1.8)和等式(1.3),使得当
,利用对偶Orlicz混合体积(1.8)和等式(1.3),使得当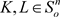 ,
, 时,可得
时,可得
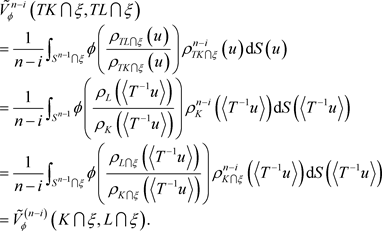
由此,当 时,根据对偶Orlicz混合仿射均质积分的定义,可得
时,根据对偶Orlicz混合仿射均质积分的定义,可得
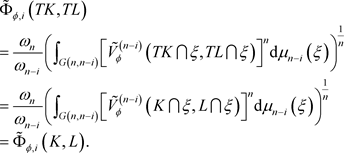
设 ,规范化的仿射均质积分的对偶conical测度
,规范化的仿射均质积分的对偶conical测度 可被定义为
可被定义为
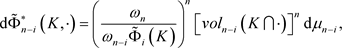 (3.1)
(3.1)
其中,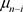 是
是 上的Haar测度。显然,规范化的仿射均质积分的对偶conical测度
上的Haar测度。显然,规范化的仿射均质积分的对偶conical测度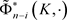 是
是 上的一个概率测度。
上的一个概率测度。
定理1.2的证明:利用对偶Orlicz混合仿射均质积分的定义(1.9),对偶仿射均质积分的定义(1.4),引理2.3,Jensen不等式(见 [14] ),Höld不等式以及严格增的凹函数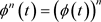 ,可得
,可得
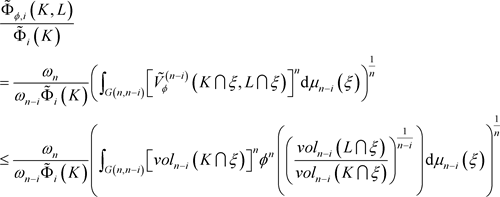
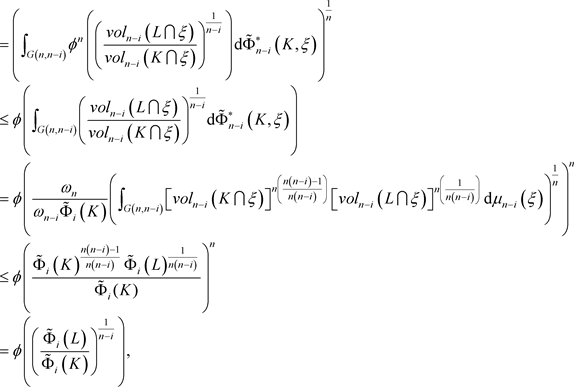
则所需不等式成立。
若上述不等式的等号成立,由于 是严格增的函数,则对偶Minkowski不等式的等号成立。因此存在
是严格增的函数,则对偶Minkowski不等式的等号成立。因此存在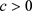 使得
使得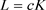 ,从而对任意
,从而对任意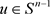 ,有
,有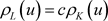 。
。
反之,当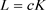 时,利用对偶Orlicz混合仿射均质积分的定义(1.9),可得
时,利用对偶Orlicz混合仿射均质积分的定义(1.9),可得
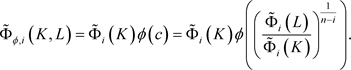
当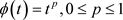 时,对偶Orlicz混合仿射均质积分的对偶Orlicz-Minkowski不等式(1.10)变为袁俊(见 [9] )的混合p次对偶仿射均质积分的Minkowski不等式(1.6)。
时,对偶Orlicz混合仿射均质积分的对偶Orlicz-Minkowski不等式(1.10)变为袁俊(见 [9] )的混合p次对偶仿射均质积分的Minkowski不等式(1.6)。
推论3.2:设 ,
, ,且
,且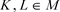 。如果
。如果
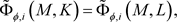 (3.2)
(3.2)
或者
 (3.3)
(3.3)
则 。
。
证明:若(3.2)成立,令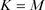 ,根据
,根据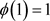 ,对偶Orlicz混合仿射均质积分的定义(1.9),以及对偶仿射均质积分的定义(1.4),得到
,对偶Orlicz混合仿射均质积分的定义(1.9),以及对偶仿射均质积分的定义(1.4),得到
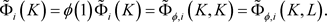
由此,利用定理1.2,可得
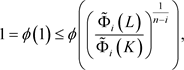
等号成立当且仅当K和L互为膨胀。因为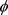 在
在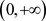 上是严格增的,则
上是严格增的,则
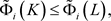
等号成立当且仅当K和L互为膨胀。如果取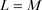 ,类似地,可得
,类似地,可得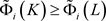 ,等号成立当且仅当K和L互为膨胀。因此,
,等号成立当且仅当K和L互为膨胀。因此,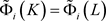 。由于K和L具有相同的对偶仿射均质积分,则
。由于K和L具有相同的对偶仿射均质积分,则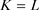 。
。
若(3.3)成立,如果令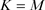 ,根据
,根据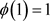 ,对偶Orlicz混合仿射均质积分的定义(1.9),以及对偶仿射均质积分的定义(1.4),得到
,对偶Orlicz混合仿射均质积分的定义(1.9),以及对偶仿射均质积分的定义(1.4),得到
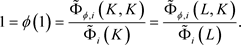
根据定理1.2,就有

等号成立当且仅当K和L互为膨胀。因为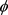 在
在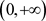 上是严格增的,则
上是严格增的,则
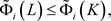
等号成立当且仅当K和L互为膨胀。如果取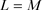 ,类似地,可得
,类似地,可得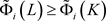 ,等号成立当且仅当K和L互为膨胀。因此,
,等号成立当且仅当K和L互为膨胀。因此, 。由于K和L具有相同的对偶仿射均质积分,则
。由于K和L具有相同的对偶仿射均质积分,则 。
。
为了证明定理1.3,我们还需以下引理:
引理3.3:设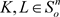 ,
,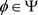 。
。
1) 如果K和L互为膨胀,那么对于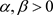 ,K和
,K和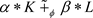 互为膨胀。
互为膨胀。
2) 设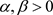 ,如果K和
,如果K和 互为膨胀,则K和L互为膨胀。
互为膨胀,则K和L互为膨胀。
证明:为了证明(1),假设存在常数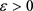 ,使得
,使得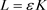 。令
。令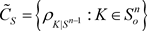 。径向Orlicz线性组合的定义表明函数
。径向Orlicz线性组合的定义表明函数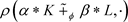 为
为

的唯一解。
另一方面,存在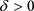 使得
使得

这意味着
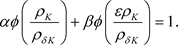
因此,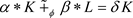 。
。
为证明(2),假设存在常数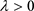 使得
使得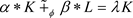 。于是对任意
。于是对任意 ,有
,有

这表明,对于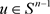 ,
,

是一个常数。由 的性质可知
的性质可知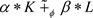 和L互为膨胀。
和L互为膨胀。
定理1.3的证明:为方便起见,令

于是,当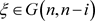 时,利用引理2.2,可得
时,利用引理2.2,可得
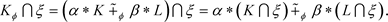
对于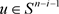 ,
,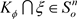 的定义表明
的定义表明
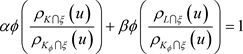 (3.4)
(3.4)
因此,利用 ,对偶仿射均质积分的定义(1.4),(3.4)式,Minkowski不等式以及定理1.2,可得
,对偶仿射均质积分的定义(1.4),(3.4)式,Minkowski不等式以及定理1.2,可得
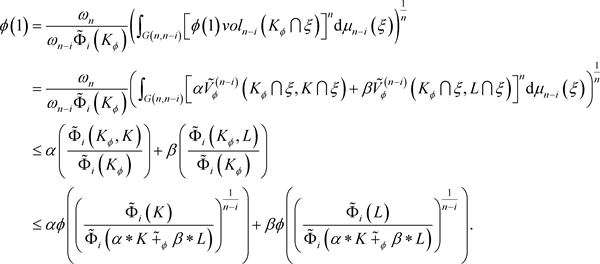
从而所需不等式得证。根据定理1.2和引理3.3,定理1.3等号成立的条件可立即得出。
当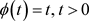 时,对偶Orlicz混合仿射均质积分的对偶Orlicz-Brunn-Minkowski不等式(1.11)变为袁俊(见 [9] )的对偶仿射均质积分的Brunn-Minkowski不等式(1.7)。
时,对偶Orlicz混合仿射均质积分的对偶Orlicz-Brunn-Minkowski不等式(1.11)变为袁俊(见 [9] )的对偶仿射均质积分的Brunn-Minkowski不等式(1.7)。
文章引用
邓国军,缑 艳. 对偶Orlicz混合仿射均质积分的不等式
Inequalities for Dual Orlicz Mixed Affine Quermassintegrals[J]. 应用数学进展, 2019, 08(12): 2035-2044. https://doi.org/10.12677/AAM.2019.812234
参考文献
- 1. Firey, W.J. (1962) p-Means of Convex Bodies. Mathematica Scandinavica, 10, 17-24.
https://doi.org/10.7146/math.scand.a-10510 - 2. Lutwak, E. (1993) The Brunn-Minkowski-Firey Theory, I: Mixed Volumes and the Minkowski Problem. Journal of Differential Geometry, 38, 131-150.
https://doi.org/10.4310/jdg/1214454097 - 3. Lutwak, E. (1996) The Brunn-Minkowski-Firey Theory, II: Affine and Geominimal Surface Areas. Advances in Mathematics, 118, 244-294.
https://doi.org/10.1006/aima.1996.0022 - 4. Ludwig, M. (2010) General Affine Surface Areas. Advances in Mathematics, 224, 2346-2360.
https://doi.org/10.1016/j.aim.2010.02.004 - 5. Lutwak, E., Yang, D. and Zhang, G. (2005) Lp John Ellipsoids. Proceedings of the London Mathematical Society, 90, 497-520.
https://doi.org/10.1112/S0024611504014996 - 6. Lv, S. and Leng, G. (2008) Lp-Curvature Images of Convex Bodies and Lp-Projection Bodies. Proceedings Mathematical Sciences, 118, 413-424.
https://doi.org/10.1007/s12044-008-0032-6 - 7. Ma, T. (2012) On the Busemann-Petty’s Problem for Lp-Intersection Body. Chinese Quarterly Journal of Mathematics, 27, 259-269.
- 8. Ma, T. (2014) The ith p-Geominimal Surface Area. Journal of Inequalities and Applications, 2014, 356.
https://doi.org/10.1186/1029-242X-2014-356 - 9. Yuan, J. and Leng, G. (2006) Inequalities for Dual Affine Quermassintegrals. Journal of Inequalities and Applications, 2006, Article No. 50181.
https://doi.org/10.1155/JIA/2006/50181 - 10. Wang, W. and Leng, G. (2005) Lp-Dual Mixed Guermassintegraks. Indian Journal of Pure and Applied Mathematics, 36, 177-188.
- 11. Lutwak, E., Yang, D. and Zhang, G. (2010) Orlicz Projection Bodies. Advances in Mathematics, 223, 220-242.
https://doi.org/10.1016/j.aim.2009.08.002 - 12. Lutwak, E., Yang, D. and Zhang, G. (2010) Orlicz Centroid Bodies. Journal of Differential Geometry, 84, 365-387.
https://doi.org/10.4310/jdg/1274707317 - 13. Gardner, R.J., Hug, D. and Weil, W. (2013) The Orlicz-Brunn-Minkowski Theory: A General Framework, Additions, and Inequalities. arXiv:1301.5267v1.
- 14. Gardner, R.J., Hug, D., Weil, W. and Ye, D. (2014) The Dual Orlize-Brunn-Minkowski Theory. arXiv:1407.7-311v1.
- 15. Zhu, B., Zhou, J. and Xu, W. (2014) Dual Orlicz-Brunn-Minkowski Theory. Advances in Mathematics, 264, 700-725.
https://doi.org/10.1016/j.aim.2014.07.019 - 16. Gardner, R.J. (2006) Geometric Tomography. Cambridge University Press, Cambridge.
https://doi.org/10.1017/CBO9781107341029 - 17. Gruber, P.M. (2007) Convex and Discrete Geometry. Springer, Berlin.
- 18. Schneider, R. (1993) Convex Bodies: The Brunn-Minkowski Theory. Cambridge University Press, Cambridge.
https://doi.org/10.1017/CBO9780511526282 - 19. Thompson, A.C. (1996) Minkowski Geometry. Cambridge University Press, Cambridge.
https://doi.org/10.1017/CBO9781107325845 - 20. Rao, M.M. and Ren, Z.D. (1991) Theory of Orlicz Spaces. Marcel Dekker, New York.
- 21. Paouris, G. and Werner, E. (2012) Relative Entropy of Cone-Volumes and Lp Centroid Bodies. Proceedings of the London Mathematical Society, 104, 253-186.
https://doi.org/10.1112/plms/pdr030 - 22. Lutwak, E. (1984) A General Isepiphanic Inequality. Proceedings of the American Mathematical Society, 90, 415-421.
https://doi.org/10.1090/S0002-9939-1984-0728360-3 - 23. Lutwak, E. (1975) Dual Mixed Volumes. Pacific Journal of Mathematics, 58, 531-538.
https://doi.org/10.2140/pjm.1975.58.531