辽宁师范大学数学学院，辽宁 大连

收稿日期：2021年12月13日；录用日期：2022年1月3日；发布日期：2022年1月18日

摘要

本文主要研究Bergman空间上以非调和函数为符号的Toeplitz算子的拟正规性和双正规性：1) 以 $\phi \left(z\right)=z^n+\lambda {\left|z\right|}^s$ 为符号的Toeplitz算子的拟正规性和双正规性；2) 以 $\psi \left(z\right)=a{z}^n{\bar{z}}^m+b{\bar{z}}^n{z}^m$ 为符号的Toeplitz算子的拟正规性和双正规性。

关键词

Bergman空间，Toeplitz算子，拟正规，双正规

Quasi-Normality and Binormality of Toeplitz Operators on Bergman Spaces

Jia Li

School of Mathematics, Liaoning Normal University, Dalian Liaoning

Received: Dec. 13^th, 2021; accepted: Jan. 3^rd, 2022; published: Jan. 18^th, 2022

ABSTRACT

In this paper, we mainly study the quasi-normality and binormality of Toeplitz operators in Bergman space with non-harmonic functions: 1) The quasi-normality and binormality of Toeplitz operators with $\phi \left(z\right)=z^n+\lambda {\left|z\right|}^s$ as symbols; 2) Quasi-normality and binormality of Toeplitz operators with $\psi \left(z\right)=a{z}^n{\bar{z}}^m+b{\bar{z}}^n{z}^m$ as symbols.

Keywords:Bergman Spaces, Toeplitz Operators, Quasi-Normality, Binormality

Copyright © 2022 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

Toeplitz算子是算子理论的组成之一，Toeplitz算子理论在概率论、控制论和物理等领域中的许多问题上都有着广泛的应用。正规算子起源于正规矩阵。如今，正规算子的理论较完备，许多学者将正规性的概念推广得到拟正规性、亚正规性、次正规性、双正规性等概念。

2019年，Gu [1] 等人介绍了Hardy空间上以解析函数或余解析函数为符号的双正规算子。进一步，对于以三角多项式和有理函数为符号的Toeplitz算子，他们证明了这些Toeplitz算子是双正规的当且仅当他们是正规的。

Bergman空间上关于Toeplitz算子的相关性质见 [2] [3] [4] [5]。1989年，Nazih [6] 证明了对于有界解析函数 $\phi$，如果 $T_{\phi }$ 或者 $T_{\bar{\phi }}$ 是拟正规的，则 $\phi$ 是一个常数。2010年，Guediri [7] 证明了若以有界解析函数或余解析函数为符号的对偶Toeplitz算子是拟正规的，则符号函数是一个常数。2020年Sumin [8] 等人给出了Bergman空间上以调和函数和非调和函数为符号的正规Toeplitz算子相关结论。

2. 预备知识

设H为无穷维复可分Hilbert空间上， $B\left(H\right)$ 为H上一切有界线性算子所构成的Banach代数。设 $\mathbb{D}$ 是复数域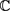上的单位圆盘，设 $\text{d}A$ 是 $\mathbb{D}$ 上的规范化面积测度。Bergman空间 $L_a^2\left(\text{d}A\right)$ 是 $L^2\left(\mathbb{D},\text{d}A\right)$ 上全体解析函数构成的空间。定义 $L_a^2\left(\text{d}A\right)$ 上的内积为

$\langle f,g\rangle ={\displaystyle {\int }_{\mathbb{D}}f\left(z\right)\overline{g\left(z\right)}}\text{d}A\left(z\right),\forall f,g\in L_a^2\left(\text{d}A\right).$

Bergman空间 $L_a^2\left(\text{d}A\right)$ 上的再生核

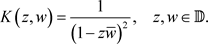
设P是 $L^2\left(\mathbb{D},\text{d}A\right)$ 到 $L_a^2\left(\text{d}A\right)$ 的正交投影，积分算子P表示为

$Pf\left(z\right)={\displaystyle {\int }_{\mathbb{D}}K\left(z,w\right)f\left(w\right)\text{d}A\left(w\right)}={\displaystyle {\int }_{\mathbb{D}}\frac{f\left(w\right)}{{\left(1-z\bar{w}\right)}^2}\text{d}A\left(w\right)}.$

设 $L^{\infty }\left(\mathbb{D}\right)$ 是 $\mathbb{D}$ 上全体本质有界可测函数构成的空间。对 $\phi \in L^{\infty }\left(\mathbb{D}\right)$，以 $\phi$ 为符号的算子 $T_{\phi }:L_a^2\left(\text{d}A\right)\to L_a^2\left(\text{d}A\right)$ 定义为

$T_{\phi }f=P\left(\phi f\right),f\in L_a^2\left(\text{d}A\right).$

则 $T_{\phi }$ 被称为Bergman空间 $L_a^2\left(\text{d}A\right)$ 上的Toeplitz算子。以 $T_{\phi }^{*}$ 定义 $T_{\phi }$ 的共轭算子。对 $\forall T_{\phi }\in L_a^2\left(\text{d}A\right)$，如果 $T_{\phi }^{*}{T}_{\phi }=T_{\phi }{T}_{\phi }^{*}$，则 $T_{\phi }$ 是正规的；如果 $T_{\phi }^{*}{T}_{\phi }{T}_{\phi }=T_{\phi }{T}_{\phi }^{*}{T}_{\phi }$，则 $T_{\phi }$ 是拟正规的；如果 $T_{\phi }{T}_{\phi }^{*}{T}_{\phi }^{*}{T}_{\phi }=T_{\phi }^{*}{T}_{\phi }{T}_{\phi }{T}_{\phi }^{*}$，则 $T_{\phi }$ 是双正规的。这三类算子之间的关系如下

$正规\to 拟正规\to 双正规$

设a和b是复数， $\phi$ 和 $\psi$ 是上的有界函数。则Toeplitz算子有如下性质：

a) $T_{a\phi +b\psi }=a{T}_{\phi }+b{T}_{\psi }$。

b) $T_{\bar{\phi }}=T_{\phi }^{*}$。

如果 $\phi \in H^{\infty }$，则

c) $T_{\psi }{T}_{\phi }=T_{\psi \phi }$。

d) $T_{\bar{\phi }}{T}_{\psi }=T_{\bar{\phi }\psi }$。

3. 以非调和函数为符号的Toeplitz算子的拟正规性和双正规性

本节主要研究了两个非调和函数，分别是 $\phi \left(z\right)=z^n+\lambda {\left|z\right|}^s$ 和 $\psi \left(z\right)=a{z}^n{\bar{z}}^m+b{\bar{z}}^n{z}^m$，并给出了Toeplitz算子拟正规和双正规的充要条件。首先介绍本文常用的一个引理：

引理3.1 [9] 如果 $k\in {\mathbb{N}}_0$ 并且 $s\in \left(0,\infty \right)$，则

1) $P\left(z^k{\left|z\right|}^s\right)=\frac{2\left(k+1\right)}{2k+s+2}{z}^k$，

2) $P\left(z^k{\bar{z}}^s\right)=\{\begin{array}{l}\frac{k-s+1}{k+1}{z}^{k-s}k\ge s\\ 0k<s\end{array}$。

命题3.2 设 $\phi \left(z\right)=z^n+\lambda {\left|z\right|}^s$，其中 $n>0$，$s\in \mathbb{N}$，$z\in \mathbb{D}$，$\lambda \in ℂ$。则

1) $T_{\phi }$ 不是拟正规的；

2) $T_{\phi }$ 是双正规的当且仅当 $\lambda =0$。

证明：1) 由引理2.1，有 $T_{\phi }1=T_{z^n+\lambda {\left|z\right|}^s}1=P\left(z^n\right)+\lambda P\left({\left|z\right|}^s\right)=z^n+\frac{2}{s+2}\lambda$，进一步 $T_{\phi }^{*}{T}_{\phi }1=\frac{1}{n+1}+{\left(\frac{2}{s+2}\right)}^2{\left|\lambda \right|}^2+\frac{2\left(n+1\right)}{2n+s+2}\bar{\lambda }{z}^n$，$n\ge 1$，再次运用引理2.1，可得

$\begin{array}{c}{T}_{\phi }{T}_{\phi }^{*}{T}_{\phi }1=\frac{2\left(n+1\right)}{2n+s+2}\bar{\lambda }{z}^{2n}+\frac{1}{n+1}{z}^n+{\left(\frac{2}{s+2}\right)}^2{\left|\lambda \right|}^2{z}^n+{\left(\frac{2\left(n+1\right)}{2n+s+2}\right)}^2{\left|\lambda \right|}^2{z}^n\\ +\frac{2}{\left(n+1\right)\left(s+2\right)}\lambda +{\left(\frac{2}{s+2}\right)}^3\lambda {\left|\lambda \right|}^2,\end{array}$

相似地，

$\begin{array}{c}{T}_{\phi }^{*}{T}_{\phi }{T}_{\phi }1=\frac{2\left(2n+1\right)}{4n+s+2}\bar{\lambda }{z}^{2n}+\frac{n+1}{2n+1}{z}^n+\frac{4\left(n+1\right)}{\left(s+2\right)\left(2n+s+2\right)}{\left|\lambda \right|}^2{z}^n+{\left(\frac{2\left(n+1\right)}{2n+s+2}\right)}^2{\left|\lambda \right|}^2{z}^n\\ +\frac{2}{\left(n+1\right)\left(s+2\right)}\lambda +\frac{2}{2n+s+2}\lambda +{\left(\frac{2}{s+2}\right)}^3\lambda {\left|\lambda \right|}^2.\end{array}$

若 $T_{\phi }$ 是拟正规的，则 $T_{\phi }{T}_{\phi }^{*}{T}_{\phi }1=T_{\phi }^{*}{T}_{\phi }{T}_{\phi }1$。若 $\lambda =0$，对比 $z^n$ 的系数，有 $\frac{1}{n+1}=\frac{n+1}{2n+1}$，矛盾；若 $\lambda \ne 0$，对比 $z^{2n}$ 的系数，有 $\frac{n+1}{2n+s+2}=\frac{2n+1}{4n+s+2}$，矛盾。因此不论 $\lambda$ 为何值， $T_{\phi }$ 都不是拟正规的。

2) 证明过程同1)，其中

$\begin{array}{c}{T}_{\phi }{T}_{\phi }^{*}{T}_{\phi }^{*}{T}_{\phi }1={\left(\frac{2\left(n+1\right)}{2n+s+2}\right)}^2{\bar{\lambda }}^2{z}^{2n}+\frac{2}{2n+s+2}\bar{\lambda }{z}^n+\frac{2}{\left(n+1\right)\left(s+2\right)}\bar{\lambda }{z}^n+{\left(\frac{2\left(n+1\right)}{2n+s+2}\right)}^3{\left|\lambda \right|}^2{z}^n\\ +{\left(\frac{2}{s+2}\right)}^3\bar{\lambda }{\left|\lambda \right|}^2{z}^n+\frac{4}{\left(2n+s+2\right)\left(s+2\right)}{\left|\lambda \right|}^2+\frac{4}{\left(n+1\right){\left(s+2\right)}^2}{\left|\lambda \right|}^2+{\left(\frac{2}{s+2}\right)}^4{\left|\lambda \right|}^4,\end{array}$

同理可得，

$\begin{array}{c}{T}_{\phi }^{*}{T}_{\phi }{T}_{\phi }{T}_{\phi }^{*}1=\frac{4\left(2n+1\right)}{\left(s+2\right)\left(4n+s+2\right)}{\bar{\lambda }}^2{z}^{2n}+\frac{2\left(n+1\right)}{\left(2n+1\right)\left(s+2\right)}\bar{\lambda }{z}^n+{\left(\frac{2}{s+2}\right)}^2\frac{2\left(n+1\right)}{2n+s+2}\bar{\lambda }{\left|\lambda \right|}^2{z}^n\\ +{\left(\frac{2\left(n+1\right)}{2n+s+2}\right)}^2\frac{2}{s+2}\bar{\lambda }{\left|\lambda \right|}^2{z}^n+\frac{2}{s+2}\left(\frac{2}{s+2}\frac{1}{n+1}+\frac{2}{2n+s+2}\right){\left|\lambda \right|}^2+{\left(\frac{2}{s+2}\right)}^4{\left|\lambda \right|}^4.\end{array}$

若 $T_{\phi }$ 是双正规的，则 $T_{\phi }{T}_{\phi }^{*}{T}_{\phi }^{*}{T}_{\phi }1=T_{\phi }^{*}{T}_{\phi }{T}_{\phi }{T}_{\phi }^{*}1$。若 $\lambda =0$，则等式成立。若 $\lambda \ne 0$，对比 $z^{2n}$ 的系数，可得 ${\left(\frac{n+1}{2n+s+2}\right)}^2\ne \frac{\left(2n+1\right)}{\left(s+2\right)\left(4n+s+2\right)}$。

当 $\lambda =0$ 时， $\phi \left(z\right)=z^n$，此时对 $\forall k$，有

$T_{\phi }{T}_{\phi }^{*}{T}_{\phi }^{*}{T}_{\phi }{z}^k=T_{z^n}{T}_{z^n{\bar{z}}^{2n}}{z}^k=\{\begin{array}{l}\frac{k-n+1}{k+n+1}{z}^k,k\ge n,\\ 0,\begin{array}{cccc}& & & k<n,\end{array}\end{array}$

$T_{\phi }^{*}{T}_{\phi }{T}_{\phi }{T}_{\phi }^{*}{z}^k=T_{{\bar{z}}^n{z}^{2n}}{T}_{{\bar{z}}^n}{z}^k=\{\begin{array}{l}\frac{k-n+1}{k+n+1}{z}^k,k\ge n,\\ 0,\begin{array}{cccc}& & & k<n,\end{array}\end{array}$

因此 $T_{\phi }$ 是双正规的当且仅当 $\lambda =0$。结论得证。

当 $n=s=1$ 时，得到一个简单的实例如下：

例3.3 设 $\phi \left(z\right)=z+\lambda \left|z\right|$，其中 $z\in \mathbb{D}$，$\lambda \in ℂ$。则

1) $T_{\phi }$ 不是拟正规的；

2) $T_{\phi }$ 是双正规的当且仅当 $\lambda =0$。

为了讨论以 $\phi \left(z\right)=a{z}^n{\bar{z}}^m+b{\bar{z}}^n{z}^m$ 为符号的Toeplitz算子的拟正规性和双正规性，首先给出一个必要的引理：

引理3.4 [8] 设 $\psi \left(z\right)=a{z}^m{\bar{z}}^n+b{\bar{z}}^t{z}^s$，其中 $m\ge n\ge 0$，$t\ge s\ge 0$，$a,b\in ℂ$ 且非零。则 $T_{\phi }$ 是正规的当且仅当 $\phi \left(z\right)$ 有形式

$\psi \left(z\right)=\left(a+b\right){\left|z\right|}^{2m}或\psi \left(z\right)=a{z}^m{\bar{z}}^n+b{\bar{z}}^m{z}^n\left(\left|a\right|=\left|b\right|\right).$

命题3.5 设 $\psi \left(z\right)=a{z}^n{\bar{z}}^m+b{\bar{z}}^n{z}^m$，其中 $n\ge m>0,a,b\in ℂ$ 且非零，则

1) $T_{\psi }$ 是拟正规的当且仅当 $\left|a\right|=\left|b\right|$，

2) $T_{\psi }$ 是双正规的当且仅当 $\left|a\right|=\left|b\right|$。

证明：1) 根据引理2.4和 $T_{\psi }$ 是正规的则 $T_{\psi }$ 是拟正规的可得充分性，下证必要性。

由引理2.1可知

$\begin{array}{c}{T}_{\psi }{z}^{n-m}=T_{a{z}^n{\bar{z}}^m+b{\bar{z}}^n{z}^m}{z}^{n-m}=aP\left(z^{2n-m}{\bar{z}}^m\right)+bP\left(z^n{\bar{z}}^n\right)\\ =a\frac{2n-2m+1}{2n-m+1}{z}^{2n-2m}+b\frac{1}{n+1},\end{array}$

再次利用引理2.1，

$\begin{array}{c}{T}_{\psi }{T}_{\psi }{z}^{n-m}=T_{a{z}^n{\bar{z}}^m+b{\bar{z}}^n{z}^m}\left(a\frac{2n-2m+1}{2n-m+1}{z}^{2n-2m}+b\frac{1}{n+1}\right)\\ =a^2\frac{3n-3m+1}{3n-2m+1}\frac{2n-2m+1}{2n-m+1}{z}^{3n-3m}\\ +ab\left[\frac{n-m+1}{{\left(n+1\right)}^2}+\frac{\left(2n-2m+1\right)\left(n-m+1\right)}{{\left(2n-m+1\right)}^2}\right]z^{n-m},\end{array}$

$\begin{array}{c}{T}_{\psi }^{*}{T}_{\psi }{z}^{n-m}=T_{\bar{a}{\bar{z}}^n{z}^m+\bar{b}{z}^n{\bar{z}}^m}\left(a\frac{2n-2m+1}{2n-m+1}{z}^{2n-2m}+b\frac{1}{n+1}\right)\\ =a\bar{b}\frac{3n-3m+1}{3n-2m+1}\frac{2n-2m+1}{2n-m+1}{z}^{3n-3m}\\ +\left[{\left|a\right|}^2\frac{\left(2n-2m+1\right)\left(n-m+1\right)}{{\left(2n-m+1\right)}^2}+{\left|b\right|}^2\frac{n-m+1}{{\left(n+1\right)}^2}\right]z^{n-m},\end{array}$

进一步，

$\begin{array}{c}{T}_{\psi }^{*}{T}_{\psi }{T}_{\psi }{z}^{n-m}=a^2\bar{b}\frac{4n-4m+1}{4n-3m+1}\frac{3n-3m+1}{3n-2m+1}\frac{2n-2m+1}{2n-m+1}{z}^{4n-4m}\\ +a{\left|a\right|}^2\frac{3n-3m+1}{{\left(3n-2m+1\right)}^2}\frac{{\left(2n-2m+1\right)}^2}{2n-m+1}{z}^{2n-2m}\\ +a{\left|b\right|}^2\frac{2n-2m+1}{2n-m+1}\left[\frac{n-m+1}{{\left(n+1\right)}^2}+\frac{\left(2n-2m+1\right)\left(n-m+1\right)}{{\left(2n-m+1\right)}^2}\right]z^{2n-2m}\\ +b{\left|a\right|}^2\frac{1}{n+1}\left[\frac{n-m+1}{{\left(n+1\right)}^2}+\frac{\left(2n-2m+1\right)\left(n-m+1\right)}{{\left(2n-m+1\right)}^2}\right],\end{array}$

同样地，

$\begin{array}{c}{T}_{\psi }{T}_{\psi }^{*}{T}_{\psi }{z}^{n-m}=a^2\bar{b}\frac{4n-4m+1}{4n-3m+1}\frac{3n-3m+1}{3n-2m+1}\frac{2n-2m+1}{2n-m+1}{z}^{4n-4m}\\ +a{\left|b\right|}^2\frac{3n-3m+1}{{\left(3n-2m+1\right)}^2}\frac{{\left(2n-2m+1\right)}^2}{2n-m+1}{z}^{2n-2m}\\ +a\frac{2n-2m+1}{2n-m+1}\left[{\left|b\right|}^2\frac{n-m+1}{{\left(n+1\right)}^2}+{\left|a\right|}^2\frac{\left(2n-2m+1\right)\left(n-m+1\right)}{{\left(2n-m+1\right)}^2}\right]z^{2n-2m}\\ +b\frac{1}{n+1}\left[{\left|b\right|}^2\frac{n-m+1}{{\left(n+1\right)}^2}+{\left|a\right|}^2\frac{\left(2n-2m+1\right)\left(n-m+1\right)}{{\left(2n-m+1\right)}^2}\right],\end{array}$

若 $T_{\psi }$ 是拟正规的，则 $T_{\psi }{T}_{\psi }^{*}{T}_{\psi }{z}^{n-m}=T_{\psi }^{*}{T}_{\psi }{T}_{\psi }{z}^{n-m}$。对比常数项，有

$\begin{array}{l}{\left|a\right|}^{2}b\frac{1}{n+1}\left[\frac{n-m+1}{{\left(n+1\right)}^2}+\frac{\left(2n-2m+1\right)\left(n-m+1\right)}{{\left(2n-m+1\right)}^2}\right]\\ =b\frac{1}{n+1}\left[{\left|b\right|}^2\frac{n-m+1}{{\left(n+1\right)}^2}+{\left|a\right|}^2\frac{\left(2n-2m+1\right)\left(n-m+1\right)}{{\left(2n-m+1\right)}^2}\right],\end{array}$

即

$\left({\left|a\right|}^2-{\left|b\right|}^2\right)\frac{n-m+1}{{\left(n+1\right)}^2}=0,$

因为 $n\ge m$，所以 $\frac{n-m+1}{{\left(n+1\right)}^2}\ne 0$，由此可得 $\left|a\right|=\left|b\right|$。

2) 同样容易得到充分性，下证必要性。通过直接的计算可得

$\begin{array}{c}{T}_{\psi }{T}_{\psi }^{*}{T}_{\psi }^{*}{T}_{\psi }1=a^2{\bar{b}}^2\frac{n-m+1}{n+1}\frac{2n-2m+1}{2n-m+1}\frac{3n-3m+1}{3n-2m+1}\frac{4n-4m+1}{4n-3m+1}{z}^{4n-4m}\\ +a\bar{b}{\left|b\right|}^2\frac{n-m+1}{n+1}\frac{3n-3m+1}{2n-m+1}\frac{{\left(2n-2m+1\right)}^2}{{\left(3n-2m+1\right)}^2}{z}^{2n-2m}\\ +a\bar{b}{\left|a\right|}^2\frac{2n-2m+1}{2n-m+1}\left[\frac{{\left(n-m+1\right)}^2\left(2n-2m+1\right)}{\left(n+1\right){\left(2n-m+1\right)}^2}+\frac{{\left(n-m+1\right)}^2}{{\left(n+1\right)}^3}\right]z^{2n-2m}\\ +{\left|a\right|}^2{\left|b\right|}^2\frac{1}{n+1}\left[\frac{{\left(n-m+1\right)}^2\left(2n-2m+1\right)}{\left(n+1\right){\left(2n-m+1\right)}^2}+\frac{{\left(n-m+1\right)}^2}{{\left(n+1\right)}^3}\right],\end{array}$

和

$\begin{array}{c}{T}_{\psi }^{*}{T}_{\psi }{T}_{\psi }{T}_{\psi }^{*}1=a^2{\bar{b}}^2\frac{n-m+1}{n+1}\frac{2n-2m+1}{2n-m+1}\frac{3n-3m+1}{3n-2m+1}\frac{4n-4m+1}{4n-3m+1}{z}^{4n-4m}\\ +a\bar{b}{\left|a\right|}^2\frac{n-m+1}{n+1}\frac{3n-3m+1}{2n-m+1}\frac{{\left(2n-2m+1\right)}^2}{{\left(3n-2m+1\right)}^2}{z}^{2n-2m}\\ +a\bar{b}{\left|b\right|}^2\frac{2n-2m+1}{2n-m+1}\left[\frac{{\left(n-m+1\right)}^2\left(2n-2m+1\right)}{\left(n+1\right){\left(2n-m+1\right)}^2}+\frac{{\left(n-m+1\right)}^2}{{\left(n+1\right)}^3}\right]z^{2n-2m}\\ +{\left|a\right|}^2{\left|b\right|}^2\frac{1}{n+1}\left[\frac{{\left(n-m+1\right)}^2\left(2n-2m+1\right)}{\left(n+1\right){\left(2n-m+1\right)}^2}+\frac{{\left(n-m+1\right)}^2}{{\left(n+1\right)}^3}\right],\end{array}$

对比 $z^{2n-2m}$ 的系数，可得

$a\bar{b}\left({\left|a\right|}^2-{\left|b\right|}^2\right)G\left(n,m\right)=0,$

其中 $G\left(n,m\right)=\frac{\left(n-m+1\right)\left(2n-2m+1\right)}{{\left(2n-m+1\right)}^2}+\frac{n-m+1}{{\left(n+1\right)}^2}-\frac{\left(2n-2m+1\right)\left(3n-3m+1\right)}{{\left(3n-2m+1\right)}^2}\ne 0$，由于 $a,b$ 非零，可得 $\left|a\right|=\left|b\right|$。

4. 研究结论

本文研究Bergman空间上Toeplitz算子的拟正规性和双正规性，并给出两个以非调和函数为符号函数的Toeplitz算子的拟正规性和双正规性的充分必要条件。

文章引用

李 佳. Bergman空间上Toeplitz算子的拟正规性和双正规性
Quasi-Normality and Binormality of Toeplitz Operators on Bergman Spaces[J]. 应用数学进展, 2022, 11(01): 126-132. https://doi.org/10.12677/AAM.2022.111018

参考文献