Pure Mathematics
Vol.06 No.03(2016), Article ID:17669,5
pages
10.12677/PM.2016.63037
A Refinement of Gronwall-Bellman Inequality
Suliang Si, Yiya Qiu, Qianqian Li, Luyao Wang, Anmin Mao
School of Mathematical Sciences, Qufu Normal University, Qufu Shandong

Received: May 7th, 2016; accepted: May 23rd, 2016; published: May 26th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
The article modifies Gronwall-Bellman inequality into vector form by the theory of differential equation and Cauchy matrix series expansion.
Keywords:Gronwall Inequality, Matrix Series, Vector

Gronwall-Bellman不等式的一个推广
司苏亮,邱意雅,李倩倩,王璐瑶,毛安民
曲阜师范大学数学科学学院,山东 曲阜

收稿日期:2016年5月7日;录用日期:2016年5月23日;发布日期:2016年5月26日

摘 要
本文用微分方程组理论和柯西矩阵级数展开作为工具,将Gronwall-Bellman不等式推广成向量形式。
关键词 :Gronwall不等式,矩阵级数,向量

1. 引言
众所周知,积分不等式在研究常微分方程和积分方程的解的性质中起着十分重要的作用 [1] - [4] 。1919年,Gronwall在研究微分方程关于参数依赖性时建立了一类基本的积分不等式,被称为Gronwall不等式,Bellman于1943年 [5] 、Bihari于1956年 [6] 得到类似的一系列不等式。目前众所周知的Gronwall-Bellman不等式结果叙述如下:
引理1.1 [2] (Gronwall-Bellman不等式) 设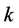 为非负常数,
为非负常数,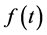 和
和 为在区间
为在区间 上的非负连续函数,且满足不等式
上的非负连续函数,且满足不等式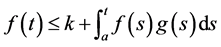 ,
,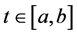 ,则有
,则有
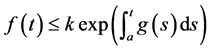 ,
,
上世纪五、六十年代以后, Gronwall-Bellman不等式被广泛用于研究常微分方程、差分方程、测度微分方程、泛函微分方程及偏微分方程的解的存在性、唯一性、有界性、稳定性等,从而引起数学家们的广泛注意,已发表的大量研究工作对不等式作了各式各样的推广。
近些年来,国内有学者通过变动上、下积分限对Gronwall-Bellman不等式结果进行一系列推广 [7] 。特别地,一些学者对Gronwall-Bellman不等式的高维情况进行了大量深入的研究 [8] [9] 。
本文的主要目的是运用Cauchy矩阵级数作为工具对Gronwall-Bellman不等式进行研究,将一维的Gronwall-Bellman不等式结果 [2] 推广到高维形式,将与线性齐次方程组有关联的Gronwall-Bellman不等式结果 [8] 推广到与线性非齐次方程组相关联的Gronwall-Bellman不等式,并给出本文所得结果在微分不等式组方面的一个应用。
首先,给出一个定理证明中用到的一个已知结果。
引理1.2 [3] 设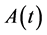 为
为 矩阵,它的元素是
矩阵,它的元素是 个函数
个函数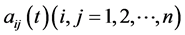 ,设
,设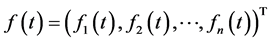 ,
,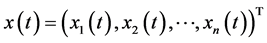 ,
,
则 ,若
,若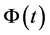 为
为 的基解矩阵,则线性方程组
的基解矩阵,则线性方程组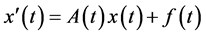 满足
满足 的解由
的解由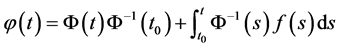 给出。
给出。
其次,为了能清晰方便地表述我们的结果,给出以下定义:
定义1 设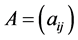 ,
,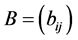 是二个
是二个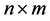 矩阵,
矩阵, 时,
时, 与
与 是二个
是二个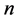 维列向量。若
维列向量。若 ,则称
,则称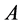 不超过
不超过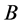 ,记为
,记为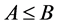 。
。 当且仅当
当且仅当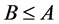 。
。
2. 主要结果及其证明
定理2.1若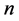 阶方阵
阶方阵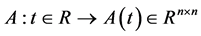 ,并且
,并且 的每个分量函数都连续,而且当
的每个分量函数都连续,而且当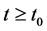 (
(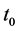 为一实常数)时,有
为一实常数)时,有
(i) ;
;
(ii) ;
;
(iii)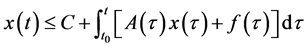 。
。
其中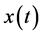 ,
, ,
,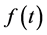 是
是 维列向量,
维列向量,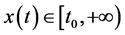 ,
,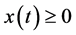 ,
,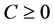 ,
,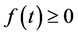 ,则当
,则当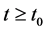 时,有
时,有
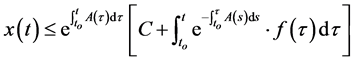
证明:令
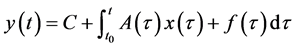
则 。将之写成
。将之写成 ,
,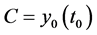 。
。
设 为
为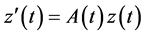 的一个标准基解矩阵,则由引理1.2知
的一个标准基解矩阵,则由引理1.2知
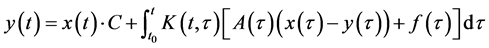
其中,
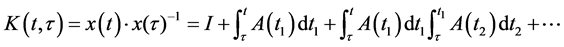
特别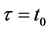 时,有
时,有
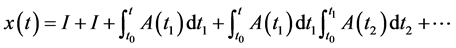
由(ii)有
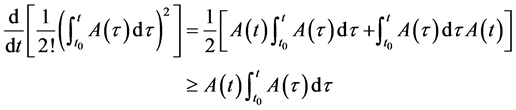
将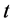 换成
换成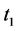 ,对在区间
,对在区间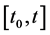 上积分上述不等式得:
上积分上述不等式得:
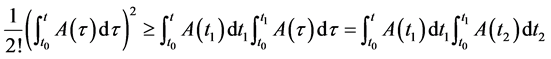
由(i)和(ii),有

将 换成
换成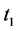 ,对在区间
,对在区间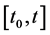 上积分上述不等式得
上积分上述不等式得
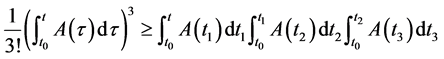 。
。
同理可得
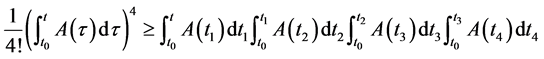 。
。
由(3),得
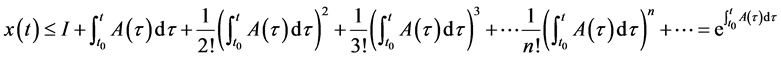
由 ,可知
,可知 ,即
,即
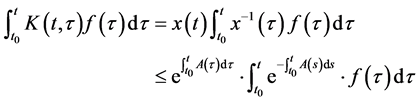
此时

这样就得到了:
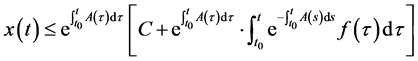
至此运用引理1.2,定理2.1得证。
注记1 若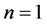 则条件(ii)成立,结论正是原始的Gronwall-Bellman引理(即本文中的引理1.1)。故本定理是此不等式的推广。
则条件(ii)成立,结论正是原始的Gronwall-Bellman引理(即本文中的引理1.1)。故本定理是此不等式的推广。
3. 应用
在本节,我们利用已得定理研究微分不等式组的解的性质。
定理3.1: 若 为
为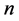 维列向量,
维列向量, 为实数,满足
为实数,满足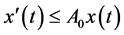 ,
,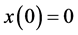 ,
,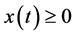 ,
,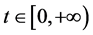 ,则
,则 。
。
证明:由条件知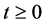 ,
, ,于是满足定理条件(i)。又因为
,于是满足定理条件(i)。又因为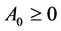 为实数,且
为实数,且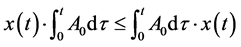 ,于是满足条件(ii)。因为
,于是满足条件(ii)。因为 ,两边在区间
,两边在区间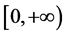 上积分得
上积分得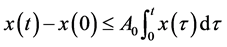 于是
于是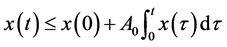 满足条件(iii)。所以
满足条件(iii)。所以
 ,其中
,其中 ,
,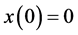 ,所以
,所以 。又因为
。又因为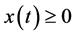 ,所以
,所以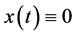 。
。
致谢
本文得到了曲阜师范大学“国家级大学生创新创业训练计划项目”(编号:201410446007)的资助,在此作者表示感谢。
文章引用
司苏亮,邱意雅,李倩倩,王璐瑶,毛安民. Gronwall-Bellman不等式的一个推广
A Refinement of Gronwall-Bellman Inequality[J]. 理论数学, 2016, 06(03): 238-242. http://dx.doi.org/10.12677/PM.2016.63037
参考文献 (References)
- 1. 尤秉礼. 常微分方程补充教程[M]. 北京: 人民教育出版社, 1981.
- 2. 王高雄, 周之铭, 朱思铭. 常微分方程[M]. 北京: 高等教育出版社, 2007.
- 3. 丁同仁. 常微分方程[M]. 北京: 高等教育出版社, 1978.
- 4. Gronwall, T.H. (1919) Note on the Derivatives with Respect to a Parameter of the Solutions of the Differential Equations. Annals of Mathematics, 20, 292-296.
- 5. Bellman, R. (1943) The Stability of Solutions of Linear Differential Equations. Duke Mathematical Journal, 10, 643- 647. http://dx.doi.org/10.1215/S0012-7094-43-01059-2
- 6. Bihari, I. (1956) Ageneralization of Bellman and Its Application to Uniqueness Problems of Differential Equations. Acta Mathematica Academiae Scientiarum Hungarica, 7, 71-94. http://dx.doi.org/10.1007/BF02022967
- 7. 李耀红, 张海燕, 芦伟. Gronwall不等式的新推广[J]. 宿州学院学报(自然科学版), 2008(23): 96-98.
- 8. 库连喜. Gronwall-Bellman不等式的一个推广[J]. 华中师范大学学报(自然科学版), 1986(2): 182-184.
- 9. 李海春, 刘召梅, 沈亮. Gronwall不等式的推广及应用[J]. 保山学院学报(自然科学版), 2010(2): 55-56.