Pure Mathematics
Vol.08 No.04(2018), Article ID:26059,8
pages
10.12677/PM.2018.84061
Orbifold K-Theory of Point Orbifolds
Yiwu Lin
School of Financial Mathematics and Statistics, Guangdong University of Finance, Guangzhou Guangdong

Received: Jul. 1st, 2018; accepted: Jul. 16th, 2018; published: Jul. 24th, 2018

ABSTRACT
In this paper we study the point orbifold, and calculate some kinds of ring structure of point orrbifolds. Then we compare the difference among these ring structures.
Keywords:Orbifold Bundle, Groupoid, Point Orbifold, Orbifold K-Theory, Representation of Finite Group, Character
点群胚的Orbifold K-理论
林奕武
广东金融学院,金融数学与统计学院,广东 广州

收稿日期:2018年7月1日;录用日期:2018年7月16日;发布日期:2018年7月24日

摘 要
本文以点群胚为例子,计算点群胚上Orbifold K-理论的几类环结构,并且比较这几类环结构之间的差异。
关键词 :Orbifold丛,群胚,点群胚,Orbifold K-理论,有限群表示,特征标

Copyright © 2018 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
Orbifold K-理论是Adem和Ruan [1] 首先提出来的。他们把orbifold X上的orbifold K-理论
定义为orbifold X上所有orbifold丛的等价类构成的Grothendieck群。若X是一个global quotient
,则
刚好是等变K-理论
。给定一个twisting
,Adem和Ruan [1] 还定义了twisted orbifold K-理论,但是他们并没有给出两类orbifold K-理论的环结构。
设X为一个紧致的近复orbifold,Adem,Ruan和Zhang [2] 考虑X上的inertia orbifold
,定义了
上的twisted orbifold K-理论
的环结构
,并称之为弦积。对于非twisted的情形,Hu和Wang [HW]定义了orbifold K-理论
的乘法
。他们通过限制映射
,
把
限制在
的每个分支上。在
上做弦积,然后利用
的左逆
拉回到
上。即
.
对于twisted的情形,Lin [L]把
分解到
上。这里
是平常的K-理论。然后在
上构造新的乘法,再拉回到
上,得到
的环结构。
本文以点群胚
为例子,计算orbifold K-理论上述两种环结构,并比较它们之间的差异。由于G是有限群,
与群代数
是线性同构的。
中的每一个元都是一个G表示。因此,计算环结构的时候可以充分利用有限群表示的理论。比如特征表的正交性等。本文得到的主要结论为定理3.1和定理3.7:
定理3.1设
,则
。
定理3.7若
且
不可约,则
其中
。
2. 准备知识
本节主要介绍Orbifold K-理论,弦积等概念,以及
中两种环结构的定义。这些概念主要来自于 [1] [2] [4] 和 [5] 。
定义2.1 [1] 设X是一个紧致的orbifold,我们称X上所有orbifold丛的等价类构成的Grothendieck群为X上的orbifold K-理论。记为
。
若X是一个global quotient
,则
刚好是
。这里
是等变K-理论,详见 [6] 。若
是一个twisting,global quotient
上的twisted orbifold K-理论定义如下。
定义2.2 [1]
上的twisted orbifold K-理论定义为所有
-twisted G-等变丛的等价类构成的Grothendieck群。记为
或
。
Orbifold X的每一个不动子集
上都有自然的orbifold结构。因此X可对应一个更大的orbifold
。称之为X的inertia orbifold。Adem,Ruan和Zhang [2] 定义了
上的弦积
。对任意
,
,
其中
分别为
为
上的阻碍丛。
在非twisted的情形,Hu和Wang [4] 利用弦积构造上的环同构。记
在其中
为每个分支
往X的嵌入映射。Hu和Wang [4] 构造
的左逆
.
上的环结构
如下定义,对任意
,
.
对于global quotient
和twisting
,Lin [L]在
上定义了乘法
。记
其中
,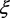 为g的特征值,
为g的属于
的特征丛。则在
之下,
为g的特征值,
为g的属于
的特征丛。则在
之下,
.
类似 [2] ,构造
的乘法如下,对任意
,
,
把这个乘法拉回到
上,便得到
的乘法
。即对于任意
,
.
3. 几类Orbifold K-理论的环结构
对于Orbifold群胚,
。若像空间
为一个单点,记为
。则态空间
为有限群,记为G。此时,称
为点群胚,或称为点Orbifold,记为
。点群胚虽然简单,但它们是Orbifold 理论中重要的例子。
本节以点群胚
为例子,利用表示论的方法,计算Orbifold K-理论的环结构
和
。
上所有的orbifold丛与G的表示群是一一对应的。我们的计算主要运用了特征标的正交性。
3.1. 一般Orbifold K-理论的环结构
的inertia orbifold 为
。其源映射和靶映射分别为
即
等价于global quotient
。其中G在自身的作用为
。因此,我们有
.
根据文 [2] ,对任意
,
.
任取
,记
分别为
在
上的限制。根据Hu和Wang [4] ,
因此,我们有
定理3.1设
,则
。
3.2. 一般Orbifold K-理论的环结构
接着,我们计算
上的另一个环结构
。我们需要用到表示论的技巧,主要是特征标的正定性。
设
为G的两个不可约表示,
分别为它们的特征标,则有正交性定理
定理3.2设
由
可以构造线性变换
.
则对任意
,
.
所以
.
因此有
命题3.3
至多只有两个特征值:0和1。
若
,则由特征标的正交性,有
.
所以得到以下定理,
定理3.4若
,则
为一个0映射。
若
。记
,
,
。取V中的一个规范正交基
使得对任意
,
都为酉矩阵。取
为其对偶基,则
。
命题3.5
的迹和秩都为1。
证明:
由命题3.3知,
的秩为1。
因为对任意
,
都是酉矩阵。则有
.
若
,
则
.
因此我们得到下面定理,
定理3.6
下面我们开始计算
上的另一个环结构
。
中的每一个丛都是一个G表示,因此我们只考虑不可约的G表示。
设
为两个不可约的G表示,则
所以,
其中,
若
,则
,因此
。
若
,取规范正交基
。对于任意
,
所以,
定理3.7若
且
不可约,则
其中
。
证明:若
,由于
,则
.
若
,由于
,则
。证毕
3.3. α-Twisted Orbifold K-理论的环结构
对于
-twisted orbifold K-理论
。根据 [5] ,存在线性同构
,
且
上的乘法为:对任意
,
,
。
因此
上的乘法为,对任意
,
其中,
根据 [3] ,对于
-twisted的情形,同样有
因此,我们有
定理3.8若
为不可约的
-twisted G表示,则
其中
。
证明:类似定理3.7。
文章引用
林奕武. 点群胚的Orbifold K-理论
Orbifold K-Theory of Point Orbifolds[J]. 理论数学, 2018, 08(04): 459-466. https://doi.org/10.12677/PM.2018.84061
参考文献
- 1. Adem, A. and Ruan, Y. (2003) Twisted Orbifold K-Theory. Communications in Mathematical Physics, 237, 533-556.
https://doi.org/10.1007/s00220-003-0849-x
- 2. Adem, A., Ruan, Y. and Zhang, B. (2007) A Stringy Product on Twisted Or-bifold K-Theory. Morfismos, 11, 33-64.
- 3. Cheng, C. (2015) A Character Theory for Projective Representations of Finite Groups. Linear Algebra and Its Applications, 469, 230-242. https://doi.org/10.1016/j.laa.2014.11.027
- 4. Hu, J. and Wang, B.-L. (2013) Delocalized Chern Character for Stringy Orbifold K-Theory. Transactions of the American Mathematical Society, 365, 6309-6341. https://doi.org/10.1090/S0002-9947-2013-05834-5
- 5. Lin, Y. (2017) Twisted Orbifold K-Theory for Global Quotient. Topology and Its Applications, 225, 9-26.
https://doi.org/10.1016/j.topol.2017.03.010
- 6. Segal, G.B. (1968) Equivariant K-Theory. Publications mathématiques de l’IHÉS, 34, 129-151.
https://doi.org/10.1007/BF02684593







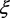 为g的特征值,
为g的属于
的特征丛。则在
之下,
为g的特征值,
为g的属于
的特征丛。则在
之下,