Pure Mathematics
Vol.
09
No.
03
(
2019
), Article ID:
30322
,
7
pages
10.12677/PM.2019.93049
Uniqueness of Difference about Entire Functions
Xiaohuang Huang, Dan Liu
Institute of Applied Mathematics, South China Agricultural University, Guangzhou Guangdong
Received: Apr. 26th, 2019; accepted: May 6th, 2019; published: May 21st, 2019

ABSTRACT
In this paper, we investigate the uniqueness of difference operators about entire function, and prove: let 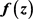 be an entire function of finite order, k be some positive integers, let
be a small function of
, and let
be the difference polynomial of
, where
are the small functions of
, and
are some finite distinct values. If
and
share 0 CM, and share
IM, then
be an entire function of finite order, k be some positive integers, let
be a small function of
, and let
be the difference polynomial of
, where
are the small functions of
, and
are some finite distinct values. If
and
share 0 CM, and share
IM, then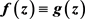 .
.
Keywords:Entire Function, Shared Small Function, Difference Polynomials

整函数差分唯一性
黄小皇,刘丹
华南农业大学应用数学研究所,广东 广州
收稿日期:2019年4月26日;录用日期:2019年5月6日;发布日期:2019年5月21日

摘 要
本文探讨整函数的差分唯一性问题,证明了:设
为开平面有穷级整函数,
为
的差分多项式,其中
为f的整小函数,
k个判别的有穷复数。又设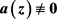 为
的一个小函数,若
与
分担0,IM分担
,则
。
为
的一个小函数,若
与
分担0,IM分担
,则
。
关键词 :整函数,分担小函数,差分多项式

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在本文中,假设读者熟知Nevanlinna值分布理论的相关基础知识以及常见符号 [1] [2] 。设a为开平面内的亚纯函数,若
,则称a为f小函数。设f与g为复平面上非常数亚纯函数,a为f与g的公共小函数,如果
与
的零点相同且每个零点重级也相同,则称f与g CM分担a。如果
与
的零点相同,不计零点重级,则称f与g IM分担a。
设k为正整数。记
为
的重级
的零点密指量,计重数。
为
的重级
的零点密指量,计重数。记
为
的重级
的零点精简密指量,不计重数。
为
的重级
的零点精简密指量,不计重数。记
为
的重级为k的零点精简密指量,不计重数。
接下来,我们需要定义一些差分算子的符号。设
为非常数亚纯函数,
为
的小函数,
为判别的有穷复数。令
为
的差分多项式。最近,许多人做了关于复差分唯一性的问题。2014年,Liu-Fang [3] 证明了:
定理A 设
为开平面有穷级的超越整函数,
为非零有穷复数,n为正整数。设
为
的两个判别的小函数。若
与
CM分担
与
,则
。
2017年,Li-Duan-Chen [4] 证明了:
定理B 设
为开平面有穷级整函数,
为非零有穷复数,n为正整数,a为有穷复数。若
与
CM0,IM分担a,则
。
本文推广并改进上述定理,证明了:
定理1 设
为开平面有穷级整函数,
为
的差分多项式,其中
为f的整小函数,
k个判别的有穷复数。又设
为
的一个小函数,若
与
分担0,IM分担
,则
。
2. 几个引理
引理1 [5] [6] [7] 设f为非常数有穷级亚纯函数,
为非零有穷复数。则
,
其中
,除去r的一个集合E,且集合E的对数测度为有穷的。
引理2 设f为非常数亚纯函数,
为阶数为p的多项式,且系数
为有穷复数。又设
为q个判别的复数,则
.
引理3 设
与
均为
上的非常数亚纯函数,则
,
其中
。
引理4 [8] 设f为有穷级
的超越亚纯函数,f是形式为方程
的一个解,其中
为f的差分多项式满足全阶
于
与
中,且
。又设所有的系数
,且对于所有的
有
。
恰好含有全阶中最大一项。则
.
引理5 设
为非常数亚纯函数,
为
的一个小函数,
。
为
的差分多项式,其中
为
的整小函数,
k个判别的有穷复数。则
i)
与
。
ii)
,与
,其中
。
证
i) 只证
。若不然,有
,即
。上式两边积分可得
,其中D为非零常数。由特征函数关系明显有
,这显然不可能。故
。同理可证
。
ii) 显然有
,故
。因为
,从而根据上式可证得
。
引理6 设f为非常数亚纯函数,
为f的三个判别的小函数。则
.
3. 定理1的证明
假设
。因为f与g CM分担0,IM分担a,则由引理1与引理6可得
,
即
。 (1)
设
, (2)
, (3)
其中
与
为引理5中所定义的。注意到f为非常数有穷级整函数,f与g CM分担0,IM分担a,我们可以知道
的极点只能为a的极点,所以有
。同理也有
。由对数导数引理以及引理5可得
, (4)
即
。设
,根据引理5有
, (5)
. (6)
因为f与g CM分担0,于是我们有
, (7)
其中
与H为整函数,且H的零点为g的极点。由引理1可得
. (8)
由引理6,(1)与(8)可得
,
即
。 (9)
由Nevanlinna第一基本定理,引理1,引理3,(5),(6),(8),(9)以及f为有穷级整函数,我们有
.
因此
。 (10)
(3)又可写成
,则由(10)可得到
. (11)
设
,其中
为正整数。接下来我们分为以下几种情形讨论。
情形1
。通过简单计算可得
,
这可推出
,其中A为非零常数。若
,则从上式恒等式可得到
,
这与(8)矛盾。因此
,于是
, (12)
其中B为非零常数。若
,明显有
,这与我们假设矛盾。故
。从(12)容易得到
. (13)
注意到
与
均为f的全阶为k的差分多项式。由引理4与(13)得
, (14)
即
。这可推出
,显然矛盾。
情形2
对任意正整数
都成立。不妨设
,即
分别为
的n重零点与
的m重零点。由(2)和(3)可推出
。所以对于所有正整数
,我们有
. (15)
于是根据引理6,(1)和(15)可以得到
(16)
即
。矛盾。于是定理1得证。
基金项目
国家自然科学基金(NO. 11701188)资助。
文章引用
黄小皇,刘 丹. 整函数差分唯一性
Uniqueness of Difference about Entire Functions[J]. 理论数学, 2019, 09(03): 370-376. https://doi.org/10.12677/PM.2019.93049
参考文献
- 1. Yang, L. (1993) Value Distribution Theory. Springer-Verlag, Berlin.
- 2. Hayman, W.K. (1964) Meromorphic Functions. Oxford University Press, London.
- 3. Liu, D., Yang. D.G. and Fang, M.L. (2014) Unicity of Entire Functions Concerning Shifts and Dif-ference Operators. Abstract and Applied Analysis, 2014, Article ID: 380910.
https://doi.org/10.1155/2014/380910
- 4. Li, S., Duan, M. and Chen, B.Q. (2017) Uniqueness of Entire Functions Sharing Two Values with Their Difference Operators. Advances in Difference Equations, Paper No. 390, 9 p.
https://doi.org/10.1186/s13662-017-1444-3
- 5. Heittokangas. Korhonen, R., Laine, I. and Rieppo, J. (2011) Uniqueness of Meromorphic Functions Sharing Values with their Shifts. Complex Variables and Elliptic Equations, 56, 81-92.
https://doi.org/10.1080/17476930903394770
- 6. Chiang, Y.M. and Feng, S.J. (2008) On the Nevanlinna Characteristic of f(z + η) and Difference Equations in the Complex Plane. The Ramanujan Journal, 16, 105-129.
https://doi.org/10.1007/s11139-007-9101-1
- 7. Halburd, R.G. and Korhonen, R.J. (2006) Nevanlinna Theory for the Difference Operator. Annales Academiæ Scientiarum Fennicæ, 31, 463-478.
- 8. Laine, I. and Yang. C.C. (2007) Clunie Theorems for Difference and q-Difference Polynomials. Journal of the London Mathematical Society, 76, 556-566.
https://doi.org/10.1112/jlms/jdm073

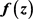 be an entire function of finite order, k be some positive integers, let
be a small function of
, and let
be the difference polynomial of
, where
are the small functions of
, and
are some finite distinct values. If
and
share 0 CM, and share
IM, then
be an entire function of finite order, k be some positive integers, let
be a small function of
, and let
be the difference polynomial of
, where
are the small functions of
, and
are some finite distinct values. If
and
share 0 CM, and share
IM, then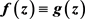 .
.

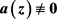 为
的一个小函数,若
与
分担0,IM分担
,则
。
为
的一个小函数,若
与
分担0,IM分担
,则
。

