Advances in Applied Mathematics
Vol.05 No.04(2016), Article ID:19087,10
pages
10.12677/AAM.2016.54084
The 1-Good-Neighbor Connectivity and Diagnosability of Möbius Cubes
Can Bai1, Shiying Wang1,2*, Zhenhua Wang1
1School of Mathematics and Information Science, Henan Normal University, Xinxiang Henan
2Henan Engineering Laboratory for Big Data Statistical Analysis and Optimal Control, Henan Normal University, Xinxiang Henan

Received: Nov. 10th, 2016; accepted: Nov. 25th, 2016; published: Nov. 29th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In the field of computers, the diagnosability of a multiprocessor is an important study topic. The traditional diagnosability allows that all neighbors of some vertices are faulty at the same time. However, in the processor system, the probability of this kind of situation is very small. Therefore, in 2012, Peng et al. proposed the g-good-neighbor diagnosability. It restrains every fault-free node containing at least g fault-free neighbors. As hypercube variants, the n-dimensional Möbius cube 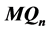 has some better properties than hypercubes. This paper shows that the 1-good-neighbor connectivity of
has some better properties than hypercubes. This paper shows that the 1-good-neighbor connectivity of 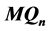 is
is 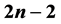 (
(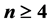 ), and the 1-good-neighbor diagnosability of
), and the 1-good-neighbor diagnosability of 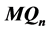 is
is 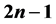 under the PMC model (
under the PMC model (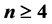 ) and under the MM* model (
) and under the MM* model (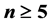 ).
).
Keywords:Interconnection Network, Möbius Cube, 1-Good-Neighbor Diagnosability

Möbius立方体的1好邻连通度和诊断度
白灿1,王世英1,2*,王贞化1
1数学与信息科学学院,河南师范大学,河南 新乡
2河南省大数据统计分析与优化控制工程实验室,河南师范大学,河南 新乡

收稿日期:2016年11月10日;录用日期:2016年11月25日;发布日期:2016年11月29日

摘 要
在计算机领域,多处理器系统的诊断度是一项重要的研究课题。在传统的诊断度中,任一处理器的所有相邻处理器可以同时出现故障。但是,在处理器系统中,出现这种情况的概率极小。因此,peng等在2012年提出了g好邻诊断度,它限制每个非故障顶点至少有g个非故障邻点。作为超立方体的变形,n维Möbius立方体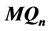 有着比超立方体更好的性质。本文证明了
有着比超立方体更好的性质。本文证明了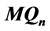 的1好邻连通度是
的1好邻连通度是 ,又证明了
,又证明了 在PMC模型下(
在PMC模型下(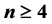 )和在MM*模型下(
)和在MM*模型下(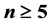 )的1好邻诊断度是
)的1好邻诊断度是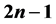 。
。
关键词 :互连网络,Möbius立方体,1好邻诊断度

1. 前言
近些年来,随着多处理器规模的扩大,处理器的稳定性对系统的正常运行起着至关重要的作用。为了保证系统的稳定性,一个处理器无论何时发生故障,它都应该及时地被非故障处理器所识别,我们把识别故障处理器的过程叫做系统的诊断。在一个系统中,如果所有的故障处理器能够被自我诊断出来,并且所诊断出的故障处理器的数量不超过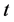 ,那么我们说这个系统是
,那么我们说这个系统是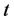 可诊断的。一个系统
可诊断的。一个系统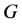 的诊断度
的诊断度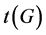 指的是
指的是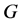 是
是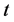 可诊断的
可诊断的 的最大值。
的最大值。
为了识别系统中的故障处理器,一些诊断模型被提出,如PMC模型和MM*模型。PMC模型 [1] 是由Preparata等首次提出,它是通过两个相邻的处理器之间相互测试来实现的。Maeng和Malek提出了另一种比较诊断模型(MM*模型) [2] 。在MM*模型下,一个顶点分别给它的两个邻点发出相同的任务,然后比较它们反馈的结果。2005年,Lai等提出了多处理器系统的一种限制诊断度,命名为条件诊断度 [3] 。2012年,Peng等通过限制每个非故障顶点至少有 个非故障邻点,提出了
个非故障邻点,提出了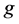 好邻诊断度 [4] ,并且他们证明了超立方体在PMC模型下的
好邻诊断度 [4] ,并且他们证明了超立方体在PMC模型下的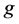 好邻诊断度是
好邻诊断度是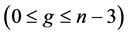
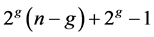 。王世英,韩威萍在文 [5] 中证明了
。王世英,韩威萍在文 [5] 中证明了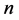 维超立方体在MM*模型下的
维超立方体在MM*模型下的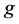 好邻诊断度。原军等在文 [6] 中证明出了
好邻诊断度。原军等在文 [6] 中证明出了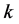 元
元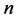 立方体在PMC模型和MM*模型下的
立方体在PMC模型和MM*模型下的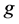 好邻诊断度是
好邻诊断度是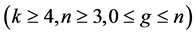
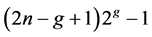 。他们在文 [7] 中还证明了3元
。他们在文 [7] 中还证明了3元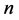 立方体的
立方体的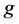 好邻诊断度。对于条件诊断度来说,其假设故障和非故障点的邻域中均至少有一个是非故障的。而对于1好邻诊断度来说,其仅假设非故障点的邻域中至少有一个是非故障的。在实际中,为节约资源和提高运算效率,大规模多处理器系统中多采用模块化设计方式。局部处理器多共享如电源、存储空间等软硬件资源且相对地数据交换频率较高。这就意味着非故障点的邻域中至少存在一个非故障点的概率远大于故障点邻域中至少存在一个非故障点的概率。鉴于此种情况,1好邻诊断度较条件诊断度更为贴合实际。马晓蕾等在文 [8] 中证明了交叉立方体的1好邻连通度和诊断度。在文 [9] 中,王牟江山等证明了网络的1好邻诊断度不超过条件诊断度。我们在这篇文章中研究Möbius立方体的1好邻连通度和诊断度。本文第二部分是预备知识,第三部分证明了Möbius立方体的1好邻连通度是
好邻诊断度。对于条件诊断度来说,其假设故障和非故障点的邻域中均至少有一个是非故障的。而对于1好邻诊断度来说,其仅假设非故障点的邻域中至少有一个是非故障的。在实际中,为节约资源和提高运算效率,大规模多处理器系统中多采用模块化设计方式。局部处理器多共享如电源、存储空间等软硬件资源且相对地数据交换频率较高。这就意味着非故障点的邻域中至少存在一个非故障点的概率远大于故障点邻域中至少存在一个非故障点的概率。鉴于此种情况,1好邻诊断度较条件诊断度更为贴合实际。马晓蕾等在文 [8] 中证明了交叉立方体的1好邻连通度和诊断度。在文 [9] 中,王牟江山等证明了网络的1好邻诊断度不超过条件诊断度。我们在这篇文章中研究Möbius立方体的1好邻连通度和诊断度。本文第二部分是预备知识,第三部分证明了Möbius立方体的1好邻连通度是
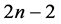 ,第四部分又证明了Möbius立方体在PMC模型下
,第四部分又证明了Möbius立方体在PMC模型下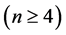 和在MM*模型下
和在MM*模型下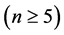 的1好邻诊断度是
的1好邻诊断度是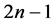 ,第五部分是结论。
,第五部分是结论。
2. 预备知识
在这部分,我们将给出文中需要的一些基本符号和概念,Möbius立方体、PMC模型、MM*模型在这部分将给出介绍。
互联网络的拓扑结构我们用图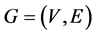 来表示,其中顶点表示处理器,边表示两处理器之间的通信链路。对于一个顶点
来表示,其中顶点表示处理器,边表示两处理器之间的通信链路。对于一个顶点 ,
,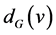 是
是 在
在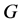 中的度,表示在
中的度,表示在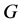 中与
中与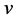 相关联的边数。对于任意一点
相关联的边数。对于任意一点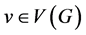 ,与
,与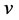 相邻的所有顶点的集合称作
相邻的所有顶点的集合称作 的邻集,记作
的邻集,记作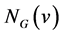 。假设
。假设 ,那么
,那么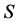 的邻集表示为
的邻集表示为 。设
。设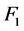 和
和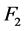 是
是 中两个不同的子集。我们将对称差记作
中两个不同的子集。我们将对称差记作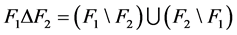 。一条路
。一条路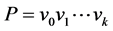 是一个所有顶点互不相同的相邻的顶点序列。如果
是一个所有顶点互不相同的相邻的顶点序列。如果 是图
是图 的边子集,且
的边子集,且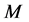 中的任意两条边没有公共顶点,则称
中的任意两条边没有公共顶点,则称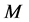 是
是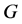 的一个匹配。如果
的一个匹配。如果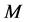 是图
是图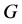 中包含边数最多的匹配,称
中包含边数最多的匹配,称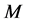 是
是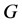 的一个最大匹配。特别地,若最大匹配饱和了
的一个最大匹配。特别地,若最大匹配饱和了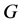 的所有顶点,称它是
的所有顶点,称它是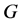 的一个完美匹配。任意一个故障集
的一个完美匹配。任意一个故障集 ,对于任意一点
,对于任意一点 ,如果
,如果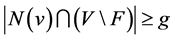 ,那么
,那么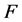 称作
称作 的
的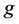 好邻故障集。如果
好邻故障集。如果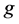 好邻故障集
好邻故障集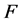 使得
使得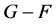 不连通,那么
不连通,那么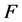 是一个
是一个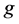 好邻割。
好邻割。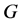 的所有
的所有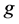 好邻割中的最小顶点数称为
好邻割中的最小顶点数称为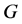 的
的 好邻连通度,记作
好邻连通度,记作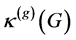 。文中其它未定义而直接使用的基本符号和概念参见文献 [10] 。
。文中其它未定义而直接使用的基本符号和概念参见文献 [10] 。
在PMC模型中,为了诊断系统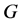 ,在
,在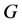 中相邻的两点之间可以相互测试。在
中相邻的两点之间可以相互测试。在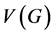 中,两个相邻的顶点
中,两个相邻的顶点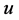 和
和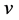 ,
,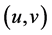 表示从
表示从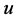 到
到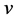 的测试,其中
的测试,其中 是测试者,
是测试者,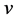 是被测试者,我们用
是被测试者,我们用 表示测试结果。在PMC模型下,所有的测试结果如表1所示。在MM*模型下,结点
表示测试结果。在PMC模型下,所有的测试结果如表1所示。在MM*模型下,结点 给它相邻的两个结点
给它相邻的两个结点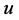 ,
,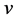 分配同一个的任务,再把测试结果反馈给结点
分配同一个的任务,再把测试结果反馈给结点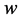 ,
,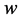 对这两个结点反馈的结果进行比较。全部的测试结果叫做这个系统的比较症候,记作
对这两个结点反馈的结果进行比较。全部的测试结果叫做这个系统的比较症候,记作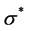 。我们用
。我们用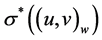 来表示测试结果。在MM*模型下,所有可能出现的比较结果如表2所示。
来表示测试结果。在MM*模型下,所有可能出现的比较结果如表2所示。
 维超立方体
维超立方体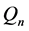 是一种很受欢迎的拓扑结构,Möbius立方体作为超立方体的一种重要变形,它有着比超立方体更好的性质。在文献 [11] 中已经给出了
是一种很受欢迎的拓扑结构,Möbius立方体作为超立方体的一种重要变形,它有着比超立方体更好的性质。在文献 [11] 中已经给出了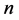 维Möbius立方体的概念,
维Möbius立方体的概念,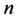 维Möbius立方体
维Möbius立方体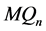 是一个有
是一个有 个顶点和
个顶点和 条边的
条边的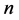 正则图。
正则图。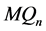 的直径大约是
的直径大约是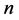 维超立方体的一半。在
维超立方体的一半。在 中,点之间的平均通信步大约是超立方体的2/3,
中,点之间的平均通信步大约是超立方体的2/3,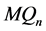 比超立方体有着更强的动态性能。因此
比超立方体有着更强的动态性能。因此 也是一种很好的网络拓扑结构,值得我们研究。
也是一种很好的网络拓扑结构,值得我们研究。
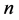 维Möbius立方体作为超立方体的变形,其有两种形式,0型
维Möbius立方体作为超立方体的变形,其有两种形式,0型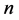 维Möbius立方体和1型
维Möbius立方体和1型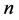 维Möbius立方体,分别记作
维Möbius立方体,分别记作 和
和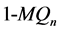 。
。
定义1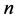 维Möbius立方体,表示为
维Möbius立方体,表示为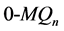 和
和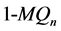 ,它的顶点集是
,它的顶点集是 。在
。在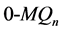 中,两个顶点
中,两个顶点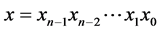 ,
,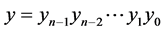 相邻当且仅当(a)存在
相邻当且仅当(a)存在 (
( )满足:
)满足:
(1) 如果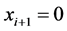 ,那么
,那么 。
。
(2) 如果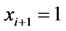 ,那么
,那么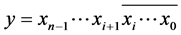 。
。
(b)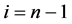 满足
满足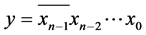 。
。
在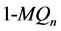 中,两个结点
中,两个结点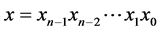 ,
,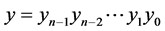 相邻当且仅当(a)存在
相邻当且仅当(a)存在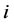 (
(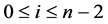 )满足:
)满足:
(1) 如果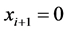 ,那么
,那么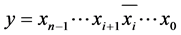 。
。
(2) 如果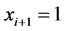 ,那么
,那么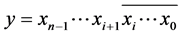 。
。
(b)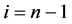 满足
满足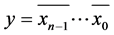 。
。
图1给出了4维的0型Möbius立方体,图2给出了4维的1型Möbius立方体。
Table 1. The test results in the PMC model
表1. 在PMC模型下测试结果
Table 2. The test results in the MM* model
表2. 在MM*模型下测试结果
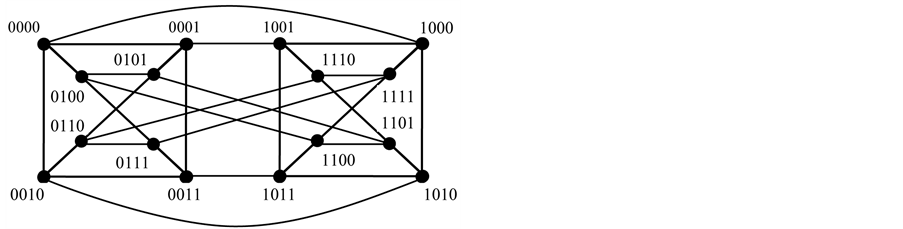
Figure 1. 4 dimensional 0 type Möbius cube
图1. 4维0型Möbius立方体

Figure 2. 4 dimensional 1 type Möbius cube
图2. 4维1型Möbius立方体
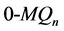 和
和 都是
都是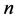 维Möbius立方体,本文只讨论
维Möbius立方体,本文只讨论 ,并把它记为
,并把它记为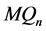 。
。
3. n维Möbius立方体的1好邻连通度
引理 3.1 [12] 当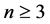 时,
时,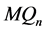 不包含三圈。
不包含三圈。
根据定义1,两个顶点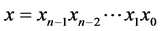 ,
,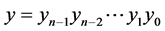 相邻当且仅当条件(b)成立,即,当
相邻当且仅当条件(b)成立,即,当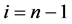 时满足
时满足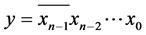 ,此时我们称顶点
,此时我们称顶点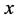 和
和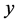 之间的连边是
之间的连边是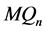 的第
的第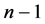 维边。我们将
维边。我们将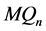 沿着最高维分解,是通过删除
沿着最高维分解,是通过删除 中所有第
中所有第 维的边,将其分解成两个
维的边,将其分解成两个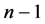 维子图
维子图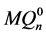 和
和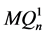 ,显然他们都同构于
,显然他们都同构于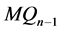 。我们称
。我们称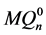 和
和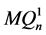 之间的连边为交叉边,这些交叉边的集合是
之间的连边为交叉边,这些交叉边的集合是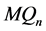 的一个完美匹配。
的一个完美匹配。
引理 3.2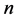 维Möbius立方体
维Möbius立方体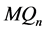 中任意两个顶点之间至多有两个公共邻点。
中任意两个顶点之间至多有两个公共邻点。
证明根据引理3.1,任意两个相邻的顶点没有公共邻点。设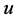 ,
, 是
是 中任意两个不相邻的顶点。用归纳法证明。当
中任意两个不相邻的顶点。用归纳法证明。当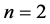 时,
时,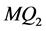 是一个四圈,此时结论成立。我们假设
是一个四圈,此时结论成立。我们假设 时结论都成立,即,
时结论都成立,即,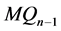 中任意两个顶点之间至多有两个公共邻点当
中任意两个顶点之间至多有两个公共邻点当 。将
。将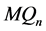 沿最高维分解成两个
沿最高维分解成两个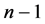 维子图
维子图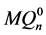 和
和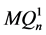 ,它们同构于
,它们同构于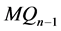 ,
, 和
和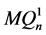 之间存在完美匹配。若
之间存在完美匹配。若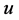 和
和 在同一个
在同一个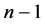 维的子图中,不失一般性,假设
维的子图中,不失一般性,假设 。由归纳假设
。由归纳假设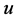 和
和 在
在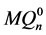 中至多有两个公共邻点。因为
中至多有两个公共邻点。因为 和
和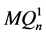 之间交叉边是一个完美匹配,所以
之间交叉边是一个完美匹配,所以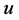 和
和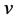 在
在 中没有公共邻点。若
中没有公共邻点。若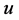 和
和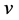 分别在两个
分别在两个 维的子图中,不失一般性,假设
维的子图中,不失一般性,假设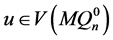 和
和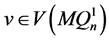 。因为
。因为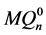 和
和 之间交叉边是一个完美匹配,所以
之间交叉边是一个完美匹配,所以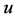 与
与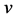 在
在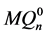 和
和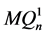 中均至多有一个公共邻点。因此,
中均至多有一个公共邻点。因此,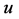 和
和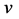 在
在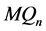 中至多有两个公共邻点。由
中至多有两个公共邻点。由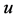 和
和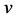 的任意性,
的任意性,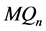 中任意两个不相邻的顶点至多有两个公共邻点。
中任意两个不相邻的顶点至多有两个公共邻点。
引理 3.3 [12]  维Möbius立方体
维Möbius立方体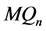 的连通度
的连通度
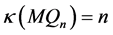 。
。
引理3.4 当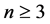 时,对任意的
时,对任意的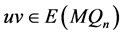 ,设
,设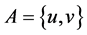 且
且 ,则
,则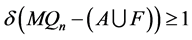 。
。
证明要证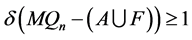 ,我们只需证明
,我们只需证明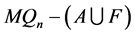 不含孤立点。当
不含孤立点。当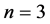 或4时,结论显然成立。当
或4时,结论显然成立。当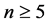 时,用反证法证明。假设
时,用反证法证明。假设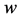 是
是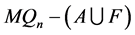 中的孤立点,则
中的孤立点,则 。因为
。因为 和
和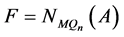 ,所以
,所以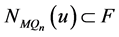 和
和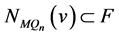 。根据引理3.2,可得
。根据引理3.2,可得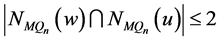 和
和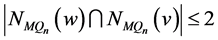 。于是,
。于是,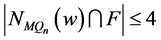 。因为
。因为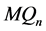 是
是 正则图,所以
正则图,所以 。因此,
。因此,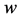 至少存在一个邻点不在
至少存在一个邻点不在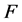 中,这与
中,这与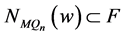 矛盾。所以
矛盾。所以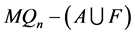 不含孤立点。故
不含孤立点。故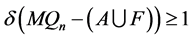 。
。
引理 3.5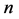 维Möbius立方体
维Möbius立方体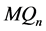 的1好邻连通度
的1好邻连通度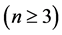
 。
。
证明 令 和
和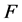 的定义与引理3.4相同,则
的定义与引理3.4相同,则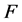 是
是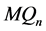 的一个割。因为
的一个割。因为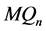 没有三圈,可以得到
没有三圈,可以得到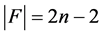 。根据引理3.4,可以推出
。根据引理3.4,可以推出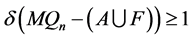 ,又因为
,又因为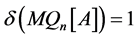 。因此,
。因此,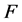 是一个1好邻割。故可以推出
是一个1好邻割。故可以推出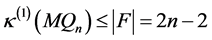 。
。
引理 3.6令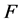 是
是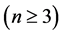
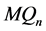 的一个点割。当
的一个点割。当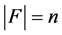 时,
时,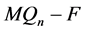 恰有两个分支,一个是平凡分支,另一个是非平凡分支。
恰有两个分支,一个是平凡分支,另一个是非平凡分支。
证明将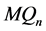 沿最高维分解成两个(
沿最高维分解成两个(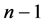 )维的子图
)维的子图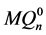 和
和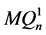 ,它们同构于
,它们同构于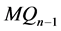 。设
。设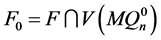 ,
,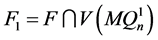 ,则
,则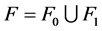 且
且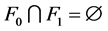 。不失一般性,我们假设
。不失一般性,我们假设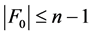 。
。
情形1 或者
或者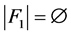 。
。
不失一般性,我们假设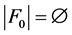 。此时
。此时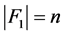 。因为
。因为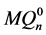 和
和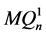 之间的交叉边是
之间的交叉边是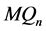 的一个完美匹配,所以
的一个完美匹配,所以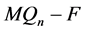 是连通的。这与
是连通的。这与 是
是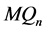 的一个点割矛盾。
的一个点割矛盾。
情形2 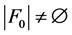 且
且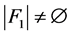 。
。
情形2.1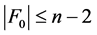 。
。
根据引理3.3,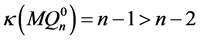 ,所以
,所以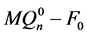 是连通的。
是连通的。
情形2.1.1 。
。
根据引理3.3, ,所以
,所以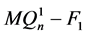 是连通的。因为
是连通的。因为
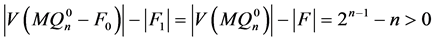 以及
以及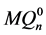 和
和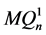 之间的交叉边是
之间的交叉边是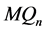 的一个完美匹配,所以
的一个完美匹配,所以 是连通的,即,
是连通的,即,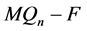 是连通的。这与
是连通的。这与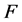 是
是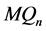 的一个点割矛盾。
的一个点割矛盾。
情形2.1.2 。
。
此时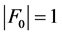 。假设
。假设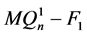 是连通的,证明同情形2.1.1。因此
是连通的,证明同情形2.1.1。因此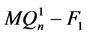 是不连通。注意到
是不连通。注意到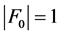 ,又因为
,又因为 和
和 之间的交叉边是
之间的交叉边是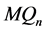 的一个完美匹配,所以
的一个完美匹配,所以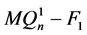 中除孤立点外的分支一定与
中除孤立点外的分支一定与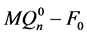 连通。因此,
连通。因此,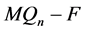 恰有两个分支,一个是平凡分支,另一个是非平凡分支。
恰有两个分支,一个是平凡分支,另一个是非平凡分支。
情形2.2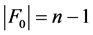 。
。
此时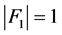 。此情形证明同情形2.1.2。
。此情形证明同情形2.1.2。
综上所述,结论成立。
引理 3.7令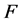 是
是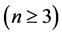
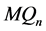 的一个点割。当
的一个点割。当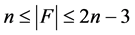 时,
时,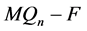 恰有两个分支,一个是平凡的,另一个是非平凡的。
恰有两个分支,一个是平凡的,另一个是非平凡的。
证明 将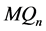 沿最高维分解成两个(
沿最高维分解成两个(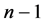 )维的子图
)维的子图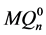 和
和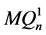 。显然,它们同构于
。显然,它们同构于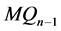 。设
。设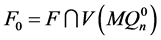 ,
,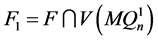 ,则
,则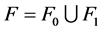 且
且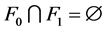 。我们采用归纳法证明。当
。我们采用归纳法证明。当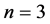 时,
时,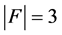 。根据引理3.6,
。根据引理3.6,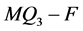 恰有两个分支,一个是平凡的,另一个是非平凡的。假设
恰有两个分支,一个是平凡的,另一个是非平凡的。假设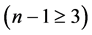
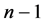 时结论也成立,即,
时结论也成立,即,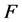 是
是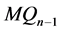 的一个点割且当
的一个点割且当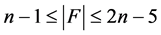 时,
时,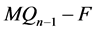 恰有两个分支,一个是平凡的,另一个是非平凡的。下面证明
恰有两个分支,一个是平凡的,另一个是非平凡的。下面证明 时结论也成立。不失一般性,假设
时结论也成立。不失一般性,假设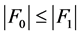 ,因为
,因为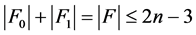 ,所以
,所以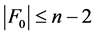 。
。
情形1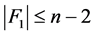 。
。
根据引理3.3,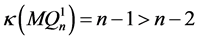 ,则
,则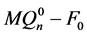 和
和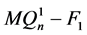 都连通。因为
都连通。因为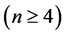
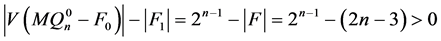 且
且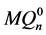 和
和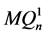 之间的交叉边是
之间的交叉边是 的一个完美匹配,所以
的一个完美匹配,所以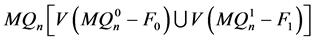 是连通的,即,
是连通的,即,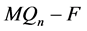 是连通的。这与
是连通的。这与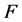 是
是 的一个点割矛盾。
的一个点割矛盾。
情形2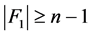 。
。
根据引理3.3,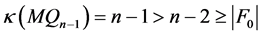 。则
。则 连通。
连通。
情形2.1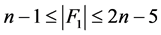 。
。
若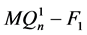 连通,证明同情形1。故
连通,证明同情形1。故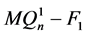 不连通。由归纳假设,
不连通。由归纳假设,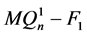 恰有两个分支,一个是平凡分支
恰有两个分支,一个是平凡分支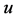 ,另一个是非平凡分支
,另一个是非平凡分支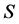 。因此,
。因此,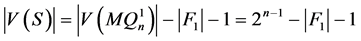 。注意到
。注意到 ,
,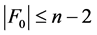 。又因为
。又因为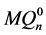 和
和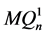 之间的交叉边是
之间的交叉边是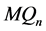 的一个完美匹配,所以
的一个完美匹配,所以
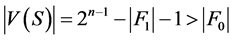 。因此,
。因此,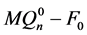 中至少有一点与
中至少有一点与 中的点相连。则
中的点相连。则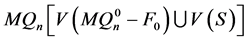 连通。若
连通。若 与
与 中的任意一点相连,那么
中的任意一点相连,那么 连通,这与
连通,这与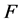 是
是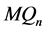 的一个点割矛盾。故
的一个点割矛盾。故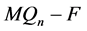 恰有两个分支,一个是平凡分支,另一个是非平凡分支。
恰有两个分支,一个是平凡分支,另一个是非平凡分支。
情形2.2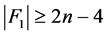 。
。
情形2.2.1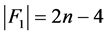 。
。
在这种情况下,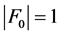 。根据引理3.3,
。根据引理3.3,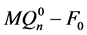 连通。若
连通。若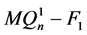 连通,证明同情形1。故
连通,证明同情形1。故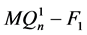 不连通。注意到
不连通。注意到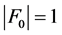 ,又因为
,又因为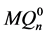 和
和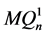 之间的交叉边是
之间的交叉边是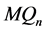 的一个完美匹配,所以
的一个完美匹配,所以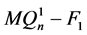 中除孤立点外的分支一定与
中除孤立点外的分支一定与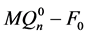 连通。因此,
连通。因此,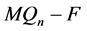 恰有两个分支,一个是平凡分支,另一个是非平凡分支。
恰有两个分支,一个是平凡分支,另一个是非平凡分支。
情形2.2.2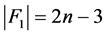 。
。
在这种情况下,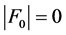 。因为
。因为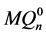 和
和 之间的交叉边是
之间的交叉边是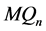 的一个完美匹配,所以
的一个完美匹配,所以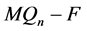 连通。这与
连通。这与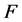 是
是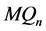 的一个点割矛盾。
的一个点割矛盾。
综上所述,结论成立。
引理 3.8 维Möbius立方体
维Möbius立方体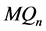 的1好邻连通度
的1好邻连通度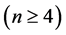
 。
。
证明我们用反证法证明,假设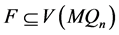 是一个1好邻割且
是一个1好邻割且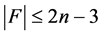 。则
。则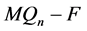 没有孤立点且不连通。根据引理3.7,当
没有孤立点且不连通。根据引理3.7,当 ,
,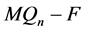 恰有两个分支,一个是平凡的,另一个是非平凡的。这与
恰有两个分支,一个是平凡的,另一个是非平凡的。这与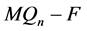 没有孤立点矛盾。因此,结论成立。
没有孤立点矛盾。因此,结论成立。
结合引理3.5和引理3.8可得以下定理:
定理 3.9 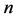 维Möbius立方体
维Möbius立方体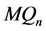 的1好邻连通度
的1好邻连通度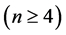
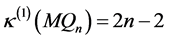 。
。
4. 在PMC模型下和MM*模型下的1好邻诊断度
在PMC模型下和MM*模型下的1好邻诊断度
定理4.1 [6] 在一个系统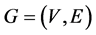 中,对于任意两个不同的且顶点个数不超过
中,对于任意两个不同的且顶点个数不超过 的
的 好邻故障集
好邻故障集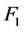 ,
,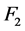 ,若
,若 ,
, 是可区分的,则
是可区分的,则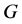 是
是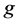 好邻条件
好邻条件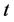 -可诊断的,使得
-可诊断的,使得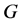 是
是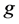 好邻条件
好邻条件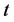 -可诊断的最大值
-可诊断的最大值 叫做
叫做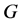 的
的 好邻诊断度,记作
好邻诊断度,记作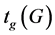 。
。
定理4.2 [6] 一个系统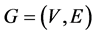 在PMC模型下是
在PMC模型下是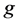 好邻
好邻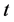 -可诊断的当且仅当对于
-可诊断的当且仅当对于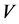 中任意两个不同的顶点数至多为
中任意两个不同的顶点数至多为 的
的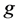 好邻故障集
好邻故障集 ,
, ,存在
,存在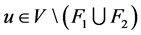 和
和 ,使得
,使得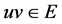 (如图3)。
(如图3)。
定理4.3 [6] 一个系统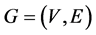 在MM*模型下是
在MM*模型下是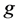 好邻
好邻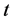 -可诊断的当且仅当对
-可诊断的当且仅当对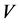 中任意两个不同的顶点数不超过
中任意两个不同的顶点数不超过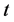 的
的 好邻故障集
好邻故障集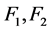 ,满足以下其中一个条件(如图4):
,满足以下其中一个条件(如图4):
(1) 存在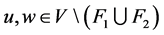 和
和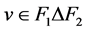 满足
满足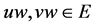 。
。
(2) 存在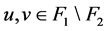 和
和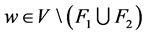 满足
满足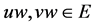 。
。
(3) 存在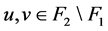 和
和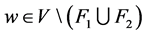 满足
满足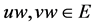 。
。

Figure 3. A distinguishable pair  under the PMC model
under the PMC model
图3. 在PMC模型下可区分对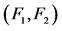

Figure 4. A distinguishable pair 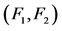 under the MM* model
under the MM* model
图4. 在MM*模型下可区分对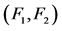
引理4.4 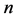 维Möbius立方体
维Möbius立方体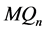 在PMC模型下和MM*模型下的1好邻诊断度
在PMC模型下和MM*模型下的1好邻诊断度
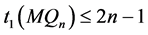 。
。
证明 对任意的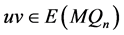 ,设
,设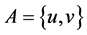 ,
,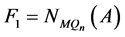 和
和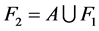 。因为
。因为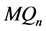 没有三圈,所以
没有三圈,所以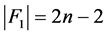 和
和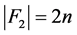 。根据引理3.4,
。根据引理3.4,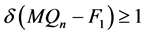 和
和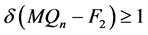 。因此,
。因此,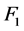 ,
, 是
是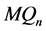 的两个1好邻故障集。因为
的两个1好邻故障集。因为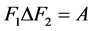 和
和 ,所以在
,所以在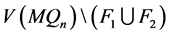 和
和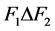 之间没有边。由定理4.2定理4.3,我们可以推出
之间没有边。由定理4.2定理4.3,我们可以推出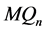 在PMC模型下和MM*模型下不是1好邻
在PMC模型下和MM*模型下不是1好邻 -可诊断的。因此,由1好邻诊断度的定义可知
-可诊断的。因此,由1好邻诊断度的定义可知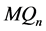 的1好邻诊断度小于
的1好邻诊断度小于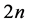 ,即
,即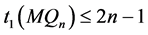 。
。
引理4.5  维Möbius立方体
维Möbius立方体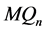 在PMC模型下的1好邻诊断度
在PMC模型下的1好邻诊断度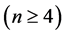
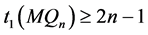 。
。
证明由1好邻诊断度的定义,需要证明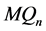 是1好邻
是1好邻 -可诊断的。根据定理4.2,证明
-可诊断的。根据定理4.2,证明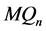 是1好邻
是1好邻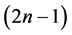 -可诊断的等价于证明任意两个不同的且顶点个数不超过
-可诊断的等价于证明任意两个不同的且顶点个数不超过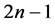 的1好邻故障集
的1好邻故障集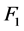 ,
, ,存在
,存在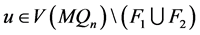 和
和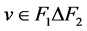 ,使得
,使得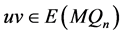 。
。
采用反证法证明。假设在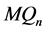 中有两个不同的且顶点个数不超过
中有两个不同的且顶点个数不超过 的1好邻故障集
的1好邻故障集 ,
,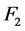 ,根据定理4.2,对任意的
,根据定理4.2,对任意的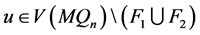 和
和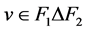 使得
使得 。不失一般性,假设
。不失一般性,假设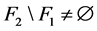 。可以分以下两种情况进行讨论:
。可以分以下两种情况进行讨论:
情形1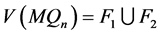 。
。
因为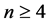 和
和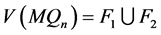 ,我们可以推出
,我们可以推出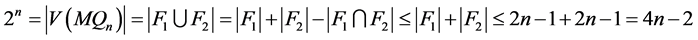 。当
。当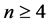 时,上述不等式矛盾。
时,上述不等式矛盾。
情形 2  。
。
根据假设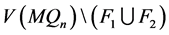 与
与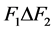 之间没有边和
之间没有边和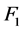 是
是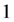 好邻故障集,可得
好邻故障集,可得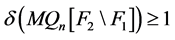 。同理,若
。同理,若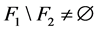 ,则
,则 。因为
。因为 ,
,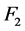 都是1好邻故障集,所以
都是1好邻故障集,所以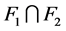 也是一个
也是一个 好邻故障集。又因为在
好邻故障集。又因为在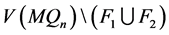 和
和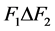 之间没有边,所以
之间没有边,所以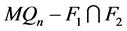 不连通。故
不连通。故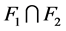 是
是 的1好邻割。根据引理3.8,可得
的1好邻割。根据引理3.8,可得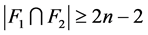 。因此,
。因此, 。这与
。这与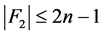 相矛盾。因为以上两种情况都产生矛盾,所以
相矛盾。因为以上两种情况都产生矛盾,所以 是1好邻
是1好邻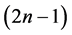 -可诊断的。由
-可诊断的。由 的定义可得,
的定义可得, 。
。
结合引理4.4和引理4.5,可得以下定理:
定理 4.6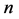 维Möbius立方体
维Möbius立方体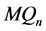 在PMC模型下的1好邻诊断度
在PMC模型下的1好邻诊断度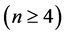
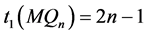 。
。
引理 4.7 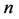 维Möbius立方体
维Möbius立方体 在MM*模型下的1好邻诊断度
在MM*模型下的1好邻诊断度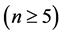
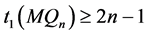 。
。
证明根据1好邻诊断度的定义,等价于证明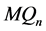 是1好邻
是1好邻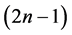 -可诊断的。采用反证法证明。根据定理4.3,假设
-可诊断的。采用反证法证明。根据定理4.3,假设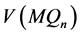 中存在两个不同的且顶点个数不超过
中存在两个不同的且顶点个数不超过 的1好邻故障集
的1好邻故障集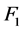 ,
,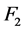 ,
,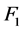 和
和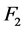 不满足定理4.3中的(1)-(3)。不失一般性,假设
不满足定理4.3中的(1)-(3)。不失一般性,假设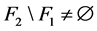 。分以下两种情况进行讨论:
。分以下两种情况进行讨论:
情形 1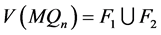 。
。
证明同引理4.5的情形1。
情形 2 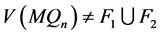 。
。
断言 1 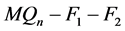 没有孤立点。
没有孤立点。
为了证明结论成立我们采用反证法。设 至少有一个孤立点
至少有一个孤立点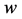 。因为
。因为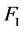 是一个1好邻故障集,所以至少存在一点
是一个1好邻故障集,所以至少存在一点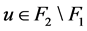 使得
使得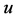 与
与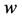 相邻。另一方面,因为
相邻。另一方面,因为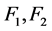 不满足定理4.3中的(1)~(3)中的任意一种条件,所以至多存在一点
不满足定理4.3中的(1)~(3)中的任意一种条件,所以至多存在一点 使得
使得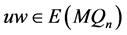 。因此仅有一点
。因此仅有一点 使得
使得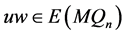 。因为
。因为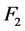 是一个1好邻故障集,所以
是一个1好邻故障集,所以 在
在 至少有一个邻点,即
至少有一个邻点,即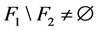 。同理,仅有一点
。同理,仅有一点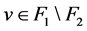 使得
使得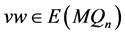 。设
。设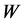 是
是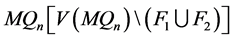 中的孤立点集,令
中的孤立点集,令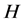 是由点集
是由点集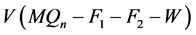 导出的子图。因此,对任意的
导出的子图。因此,对任意的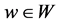 ,存在
,存在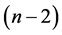 个邻点在
个邻点在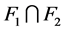 中。由于
中。由于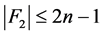 ,故
,故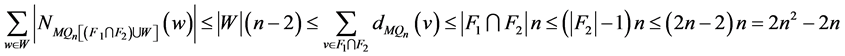 。因为
。因为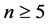 ,所以
,所以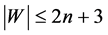 。假设
。假设 ,有
,有 。当
。当 时,上式矛盾,故
时,上式矛盾,故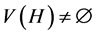 。因为
。因为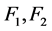 不满足定理4.3中的(1)且
不满足定理4.3中的(1)且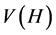 的任意一点是不孤立的,所以可以推出
的任意一点是不孤立的,所以可以推出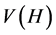 与
与 之间不存在边相连。因此,
之间不存在边相连。因此,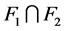 是
是 的点割且
的点割且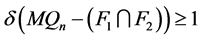 ,即
,即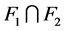 是
是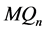 的一个1好邻割。根据定理3.8,
的一个1好邻割。根据定理3.8,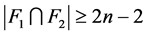 。 因为
。 因为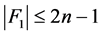 ,
,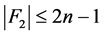 并且
并且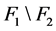 和
和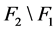 都是非空的,所以
都是非空的,所以 。于是,设
。于是,设 和
和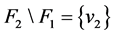 。所以对于任意的
。所以对于任意的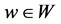 满足
满足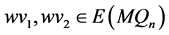 。根据引理3.2,
。根据引理3.2,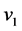 与
与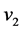 在
在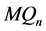 中至多有两个公共邻点。因此,
中至多有两个公共邻点。因此, 至多有两个孤立点。
至多有两个孤立点。
假设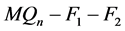 中恰有一个孤立点
中恰有一个孤立点 ,则
,则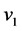 ,
, 在
在 中与
中与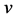 相邻。显然,
相邻。显然,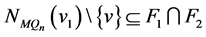 ,
,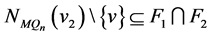 ,
,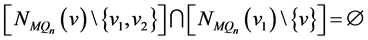 和
和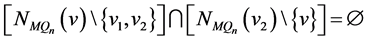 。根据引理3.2,
。根据引理3.2,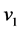 与
与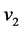 在
在 至多有两个公共邻点,所以
至多有两个公共邻点,所以 。因此,
。因此,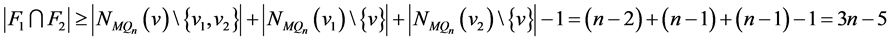 。于是,
。于是,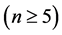
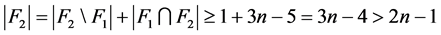 。这与
。这与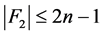 矛盾。
矛盾。
假设在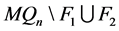 中还有另外一个孤立点
中还有另外一个孤立点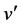 ,则
,则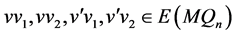 ,
,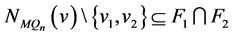 和
和 。根据引理3.1,可以得到
。根据引理3.1,可以得到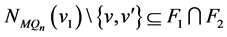 和
和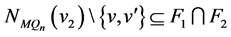 。又因为在
。又因为在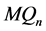 中任意两点至多有两个公共邻点,所以
中任意两点至多有两个公共邻点,所以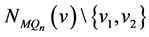 ,
, ,
,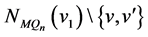 和
和 中任意两个集合在
中任意两个集合在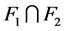 中都没有公共点。因此
中都没有公共点。因此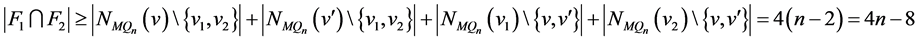 。于是,
。于是,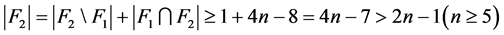 ,这与
,这与 矛盾。断言1证明完毕。
矛盾。断言1证明完毕。
设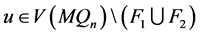 。根据断言1,
。根据断言1,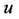 在
在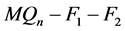 中至少有一个邻点。因为
中至少有一个邻点。因为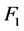 ,
,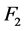 不满足定理4.3中的(1)~(3)中的任意一种条件,根据定理4.3(1),所以对于任意一对相邻的点
不满足定理4.3中的(1)~(3)中的任意一种条件,根据定理4.3(1),所以对于任意一对相邻的点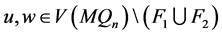 ,不存在
,不存在 使得
使得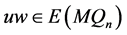 和
和 。因此,我们可以得到
。因此,我们可以得到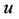 在
在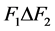 中没有邻点。由
中没有邻点。由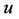 的任意性,
的任意性, 与
与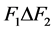 之间没有边。因为
之间没有边。因为 是一个1好邻故障集且
是一个1好邻故障集且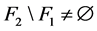 ,所以
,所以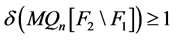 ,则
,则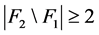 。因为
。因为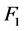 和
和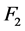 都是1好邻故障集并且
都是1好邻故障集并且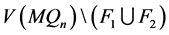 与
与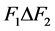 之间没有边,所以
之间没有边,所以 是
是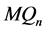 的一个1好邻割。根据引理3.6,有
的一个1好邻割。根据引理3.6,有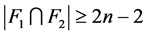 。因此,
。因此,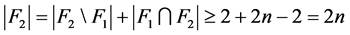 。这与
。这与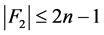 矛盾。于是,
矛盾。于是, 是1好邻
是1好邻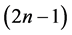 -可诊断的。故
-可诊断的。故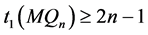 。
。
结合引理4.4和引理4.7可得以下定理:
定理 4.8 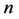 维Möbius立方体
维Möbius立方体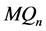 在MM*模型下的1好邻诊断度
在MM*模型下的1好邻诊断度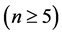
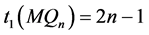 。
。
5. 结论
在这篇文章中,我们研究了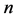 维Möbius立方体
维Möbius立方体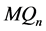 在两种模型下的1好邻诊断度问题。本文证明了Möbius立方体的1好邻连通度是
在两种模型下的1好邻诊断度问题。本文证明了Möbius立方体的1好邻连通度是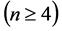
 ,又证明了Möbius立方体在PMC模型下的1好邻诊断度是
,又证明了Möbius立方体在PMC模型下的1好邻诊断度是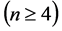
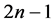 和在MM*模型下的1 好邻诊断度是
和在MM*模型下的1 好邻诊断度是
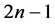 。1好邻诊断度是假设每个非故障点至少有1个好的邻点,
。1好邻诊断度是假设每个非故障点至少有1个好的邻点, 好邻诊断度是假设每个非故障点至少有
好邻诊断度是假设每个非故障点至少有 个好的邻点。这项工作将对后面研究Möbius立方体网络的
个好的邻点。这项工作将对后面研究Möbius立方体网络的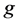 好邻连通度、诊断度和相关诊断算法提供很好的帮助。
好邻连通度、诊断度和相关诊断算法提供很好的帮助。
基金项目
国家自然科学基金资助项目(61370001),教育部博士点基金(博导类)资助项目(20111401110005)。
文章引用
白灿,王世英,王贞化. Mo¨bius立方体的1好邻连通度和诊断度
The 1-Good-Neighbor Connectivity and Diagnosability of Mo¨bius Cubes[J]. 应用数学进展, 2016, 05(04): 728-737. http://dx.doi.org/10.12677/AAM.2016.54084
参考文献 (References)
- 1. Preparata, F., Metze, G. and Chien, R.T. (1968) On the Connection Assignment Problem of Diagnosable Systems. IEEE Transactions on Electronic Computers, 12, 848-854.
- 2. Joon, M. and Miroslaw, M. (1981) A Comparison Connection Assignment for Self-Diagnosis of Multiprocessor Systems. Proceeding of 11th International Symposium on Fault-Tolerant Computing, 173-175.
- 3. Lai, P.-L., Tan, J.J.M., Chang, C.-P. and Hsu, L.-H. (2005) Conditional Diagnosability Measures for Large Multiprocessor Systems. IEEE Transactions on Computers, 54, 165-175. https://doi.org/10.1109/TC.2005.19
- 4. Peng, S.-L., Lin, C.-K., Tan, J.J.M. and Hsu, L.-H. (2012) The g-Good-Neighbor Conditional Diagnosability of Hypercube under the PMC Model. Applied Mathematics Computation, 218, 10406-10412. https://doi.org/10.1016/j.amc.2012.03.092
- 5. Wang, S.Y. and Han, W.P. (2016) The g-Good-Neighbor Conditional Diagnosability of n-Dimensional Hypercubes under the MM* Model. Information Processing Letters, 116, 574-577. https://doi.org/10.1016/j.ipl.2016.04.005
- 6. Yuan, J., Liu, A.X., Ma, X., Liu, X.L., Qin, X. and Zhang, J.F. (2015) The g-Good-Neighbor Conditional Diagnosability of k-Ary n-Cubes under the PMC Model and MM* Model. IEEE Transactions on Parallel and Distributed Systems, 26, 1165-1177. https://doi.org/10.1109/TPDS.2014.2318305
- 7. Yuan, J., Liu, A.X., Qin, X., Zhang, J.F. and Li, J. (2016) g-Good-Neighbor Conditional Diagnosability Measure of 3-Ary n-Cube Networks. Theoretical Computer Science, 626, 144-162
- 8. Ma, X.L., Wang, S.Y. and Wang, Z.H. (2016) The 1-Good-Neighbor Connectivity and Diagnosability of Crossed Cube. Advance in Applied Mathematics, 5, 282-290.
- 9. Wang, M., Guo, Y.B. and Wang, S.Y. (2015) The 1-Good-Neighbor Diagnosability of Cayley Graphs Generated by Transposition Trees under the PMC Model and MM* Model. International Journal of Computer Mathematics, 1-12. https://doi.org/10.1080/00207160.2015.1119817
- 10. Bondy, J.A. and Murty, U.S.R. (2007) Graph Theory. Springer, New York.
- 11. Cull, P. and Larson, S.M. (1995) The Möbius Cubes. IEEE Transactions on Computers, 44, 647-659. https://doi.org/10.1109/12.381950
- 12. Fan, J.X. (1998) Diagnosability of Möbius Cubes. IEEE Transactions on Parallel and Distributed Systems, 9, 923-928. https://doi.org/10.1109/71.722224
*通讯作者。
