Advances in Applied Mathematics
Vol.
10
No.
01
(
2021
), Article ID:
39898
,
12
pages
10.12677/AAM.2021.101019
改进的T_TIDE程序包在潮汐中的应用
刘倩,孙小淇
青岛大学数学与统计学院,山东 青岛
收稿日期:2020年12月19日;录用日期:2021年1月15日;发布日期:2021年1月21日

摘要
基于独立点格式和三次样条插值,提出了一种新的处理非平稳潮汐的增强调和分析方法。该方法从T_TIDE程序包中开发出来,通过MATLAB工具箱S_TIDE实现。通过分析青岛港观测站逐时的潮位观测数据,进行灵敏度实验,讨论独立点数的选择。结果表明,当独立点个数为1时,S_TIDE与T_TIDE方法得到的回报潮汐水位、潮汐组成特性平和均海平面变化特性相似。随着独立点个数的不断增加,非线性趋势越来越明显,峰值和谷值点的个数递增,平均海平面显示出更多的振荡。因此,S_TIDE理论上可以应用于各种非平稳潮汐。
关键词
经典调和分析,T_TIDE程序包,S_TIDE工具箱,独立点格式,三次样条插值
Application of Improved T_TIDE Package in Tide
Qian Liu, Xiaoqi Sun
School of Mathematics and Statistics, Qingdao University, Qingdao Shandong

Received: Dec. 19th, 2020; accepted: Jan. 15th, 2021; published: Jan. 21st, 2021

ABSTRACT
Based on the independent point scheme and cubic spline interpolation, a new approach, enhanced harmonic analysis, was developed to deal with non-stationary tides. Enhanced harmonic analysis is realized by a MATLAB toolbox, S_TIDE, which is developed from the widely used T_TIDE. By analyzing the tide level observation data of Qingdao port observation station, the sensitivity experiment was carried out and the choice of independent points was discussed. The results show that when the number of independent points is 1, the returns of S_TIDE and T_TIDE are similar in tidal level, tidal composition and mean sea level. As the number of independent points increases, the nonlinear trend becomes more and more obvious, the number of peak and valley points increases, and the mean sea level shows more oscillations. Therefore, S_TIDE can be theoretically applied to all kinds of non-stationary tides.
Keywords:Classical Harmonic Analysis, T_TIDE Package, S_TIDE Toolkit, Independent Point Scheme, Cubic Spline Interpolation

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
海洋表面因受天体运动产生引潮力的作用,海水会出现周期性涨落的现象,这一现象称为潮汐 [1]。中国海域辽阔,潮汐分析在航海工作、海洋资源开发、军事发展和经济建设等各个领域都起到重要的作用。青岛港位于黄海西海岸,半岛南岸西部的胶州湾口附近,面临黄海,背依崂山。港内水域宽阔,水深浪静,港口设备完善,系泊条件良好,各类船舶昼夜进出均较方便,为我国著名的天然良港。
对潮汐的研究人们最早运用经典调和分析法,其通过普通最小二乘回归确定振幅和相位。经典调和分析假设水位只受潮汐的影响,潮汐是完全静止的 [2]。然而,所有潮汐时间序列在理论上都是非平稳的。非潮波扰动,如风暴潮等,可在观测中产生非平稳成分。在大多数沿海潮汐高程观测中,非平稳成分非常小,潮汐可以被认为是几乎静止的。因此,经典调和分析在潮汐观测中表现很好,通常95%以上的方差可用不到150个成分进行解释。但有许多潮汐过程受到非潮汐扰动的高度影响,包括内部潮汐、河流潮汐等 [3]。在此情况下,由于不切实际的平稳假设,经典调和分析表现不佳。为了深入了解非平稳潮汐数据的基本动力学,采用了几种方法 [4],如复杂解调、连续小波变换和短期调和分析,可以在时间和频域上呈现不同的振幅,反映非潮汐过程的影响,但潮带内成分的分辨率有限 [5]。此外,这些方法不能定义非平稳潮汐中重要的潮下波动 [2]。
Matte等 [5] [6] 根据Kukulka和Jay等 [7] [8] 提出的阶段和潮汐流模型,通过修改T_TIDE [9],开发了一个非平稳性潮汐分析工具NS_TIDE,将其用于河流潮汐。NS_TIDE使用了一个稳健的回归 [10] [11],并将河流流量的非平稳强迫直接建立到调和分析基函数中。然而,尽管NS_TIDE具有预测能力,但有两个局限性:第一,需要精确的河流流量数据;第二,专门分析河流潮汐,不能与其它动态机制一起应用于非平稳潮汐,例如内部潮汐。
基于独立点(IP)格式和三次样条插值,Jin等开发了增强调和分析,并将该算法应用于南海内部潮流,确定了随时间变化的调和参数 [12]。但由于观测有限和物理过程的复杂,Jin等人没有说明如何为增强调和分析选择IP编号。2018年,潘海东等 [13] 提出了一种新的处理非平稳潮汐的增强调和分析方法,应用于分析河流潮汐水位记录,还将该方法与其它方法进行比较。
本文在MATLAB工具箱S_TIDE中实现了增强调和分析。S_TIDE应用于分析青岛港观测站的潮汐水位记录,并与T_TIDE进行比较,以显示其效率。为验证该方法的实用性,还分析了日本的钏路(Kushiro)验潮站的潮汐水位数据。
2. 数据
青岛港口位于胶州湾口东北方,即36˚05'.3N,120˚19'.0E (见图1),港池由防波堤环抱而成,其入口呈喇叭形向西南敞开,最窄处宽约270米,港池内水深一般为5~13米。港池多为大型固定码头,系泊条件良好,国内外远洋船舶多停泊于此进行装卸作业。本文收集了青岛港观测站2019年1月1日至2020年2月29日共10200组逐时潮汐水位观测资料,实验数据源于中国港口网(http://www.chinaports.com/tidal)。
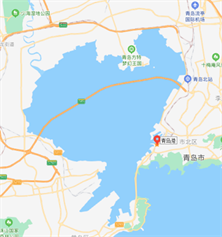
Figure 1. Location of Qingdao Port
图1. 青岛港口的地理位置
3. 分析方法
3.1. 经典的调和分析法
在经典的调和分析方法中,潮汐水位可用正弦项的线性组合来表示 [14]:
(1)
其中, 是时间t的水位。 、 和 分别是第j个潮汐的频率、振幅和相位。 是平均海平面。引入新的未知数 和 ,重写方程(1)将其线性化:
(2)
其中:
在回归分析中,方程(2)可以用矩阵形式写成 ,其中Z是水位向量,A是在测量计算时的基函数矩阵,x是未知参数向量。经典调和分析方法通常使用普通最小二乘法进行,这使每个数据点在解中的权重相等。为缩小置信区间,需用标准来限制调和分析中成分的数量。Godin使用瑞利分离方程 [15]:
(3)
其中: 和 是两个相邻的潮汐频率,m是样本的数量, 是样本间隔, 是记录的长度。在用瑞利准则确定最小允许频率分离后,以潮势振幅作为后验,决定列入的顺序。
本文使用T_TIDE程序包执行带有节点校正、推理的经典调和分析,选择传统的最小二乘法求解青岛港口观测站的调和常数数,并用Matlab R2016a加载和分析时间序列,对青岛港每日不同时刻的潮位情况数据进行分析。其中t_tide.m用于分析,t_predic.m用于潮汐预报。具体步骤如下:
1) 数据预处理。对原始数据资料的个别奇异点进行中值滤波处理,剔除毛刺,对极少部分缺测资料利用Gil等(2005)介绍的最小二乘插值法进行插值 [16],并将该时间序列转换成格林威治时间。
2) 程序实现。首先读取数据,目的是为了将原始数据一列的读取在变量中。接着使用t_tide分析逐时的潮位资料,得到输出参数分潮的符号(name)、振幅(amp)、迟角(pha)、信噪比(snr)、回报的潮位(xout)等。一般认为snr > 2的分潮是显著的。
3) 潮汐预报。调和分析结束后用t_predic进行潮汐的预报,得到不含计算数据平均值的预报潮位。
运行Matlab软件,对青岛港观测站1年多的潮位数据的进行经典调和分析,得到67个分潮成分,按振幅贡献率排名,取其中最大的8种成分的振幅、迟角和信噪比于下表1中。
Table 1. The harmonic constants of the main tidal components
表1. 主要分潮的调和常数
由表1知,青岛港潮汐以M2分潮为主,其次为S2、N2、K1、O1和SA等分潮,受半日分潮影响显著,与青岛港为正规半日潮港相契合。其中振幅贡献率前三名为半日分潮M2、S2和N2,主要全日分潮K1和O1的振幅分别约为半日分潮M2的0.1857倍和0.1531倍;太阳年周潮SA的振幅为20.9708 cm;主要浅水分潮M4的振幅为13.6372 cm。
在上述分析中不包含节点修正,因为与阶段变化的影响相比,河流潮汐的节点调制通常很小 [5]。为与T_TIDE的结果进行比较,下文也不对S_TIDE确定的潮汐特性进行节点修正。使用T_TIDE程序包,青岛港观测站的回报只解释了原始信号方差的89.4%,潮汐高度的均方根误差(RMSE)为37.181 cm。故经典调和分析方法具有一定的局限性,因此对该方法进行改进是学者未来研究的方向。
3.2. 增强的调和分析法
新提出的增强调和分析还假定同T_TIDE一样的时变 、 和 :
(4)
在用IP方案求解方程(4)时,S_TIDE与NS_TIDE不同 [16] [17] [18] [19]。IP方案的基本思想非常简单 [7] [8]。假设调和参数(例如振幅)是时变的, 是时间指数。首先,选择IP的索引,即 作为参数空间的代表。 是X的子集。第二,计算IP处的调和参数。最后,在IP之间插值其它点 上的调和参数 [12]。X被命名为独立点,因为其他点的值是通过在IP上插值值获得的,或者在某种意义上,它们依赖于IP上的值 [20]。
下面介绍增强调和分析的主要思想。在IP上均匀分布的平均海平面和潮汐系数被选择为独立参数(表示为 、 和 ),而在其它点上的平均海平面和潮汐系数则是通过IP之间的插值得到的。因此,变化的平均海平面和潮汐系数可以用 、 和 的函数来表示,它们是:
(5)
其中, 是时间t的第i个IP的插值权重,其值取决于插值方法。MS和M分别是平均海平面和成分的IP编号。目前为止 、 和 的值未知,但可通过插值得到,时变 、 和 可分别表示为 、 和 值的线性组合,方程(4)和(5)的组合产生方程(6):
(6)
三次样条插值由于其稳定、收敛和平滑的特性而被广泛应用 [18] [21] [22]。故在本方案中采用三次样条插值计算。当在N矩处测量,即在 时 ,我们得到以下方程集:
(7)
方程(7)中的 的总和是未知数,当观察记录数量N远大于 时,可被估计出来。此外, 、 和 可通过最小二乘拟合估计,在对其进行插值,可得到时变平均海平面、振幅等。
下面介绍误差估计算法 [12]。首先,从原始观测时间序列中去除增强调和分析估计的潮部和潮下部,以获得残余或噪声。然后,通过重采样残差的时间序列,产生合成噪声实现。第三,将潮汐部分和潮下部分加入到每个噪声实现中,通过最小二乘拟合得到潮汐部分和潮下部分的新估计。最后,利用t分布可以计算置信区间。在S_TIDE中,组成选择取决于IP的数量。
4. 结果分析
4.1. S_TIDE与T_TIDE结果比较
S_TIDE可以求解分潮时间变化的振幅和迟角,但是当独立点个数取1时,振幅和迟角都是常数,此时S_TIDE计算结果与T_TIDE相同。下面比较独立点个数取1时S_TIDE与T_TIDE的计算结果,如图1所示。使用Matlab软件加载青岛港观测站的逐时潮汐水位数据,运行S_TIDE与T_TIDE程序包进行潮汐水位数据的回报(见图2)。进行分析时,若未指定具体分潮,S_TIDE会根据数据长度和瑞利准则自动选取分潮,通过上述经典调和分析的讨论,本文的仿真实验选取振幅贡献率较大的8个分潮M2、S2、N2、K1、O1、SA、M4、K2去求解回报潮汐水位。
由图2知,当独立点个数为1时,T_TIDE和S_TIDE程序包计算得到的回报潮汐水位变化趋势一致,故当独立点个数取1时,S_TIDE计算结果与T_TIDE相同。当独立点个数由1增加到3时,两者回报的潮位出现差值,差值在两端和中间位置的值最大。S_TIDE程序包不仅包含了T_TIDE的回报水位功能,且还能选择独立点个数,故更好的验证了新开发的S_TIDE 程序包的有效性和实用性。
S_TIDE程序包可求解各分潮随时间变化的振幅和迟角以及变化的平均海平面。当独立点个数取1时,反演结果为常数,与T_TIDE的结果相同;当独立点取2时,反演结果为线性变化,当取更多的独立点时,变化更为复杂。一般来说,不同独立点反演的结果代表了不同时间尺度上的波动。
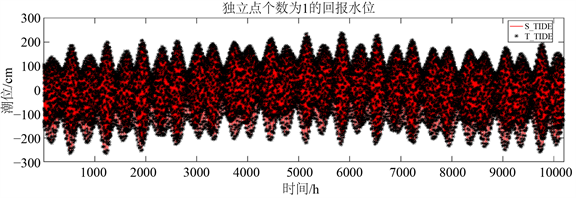
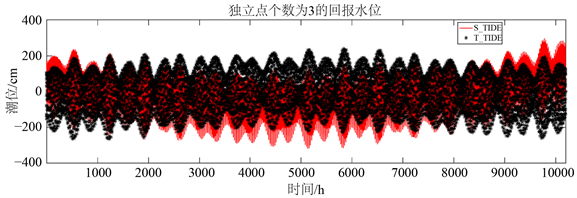
Figure 2. S_TIDE comparison of T_TIDE return water level
图2. S_TIDE与T_TIDE回报水位对比
4.2. S_TIDE的求解
S_TIDE程序包可求解各分潮随时间变化的振幅和迟角以及变化的平均海平面。当独立点个数取1时,反演结果为常数,与T_TIDE的结果相同;当独立点取2时,反演结果为线性变化,当取更多的独立点时,变化更为复杂。一般来说,不同独立点反演的结果代表了不同时间尺度上的波动。
4.2.1. 振幅的变化
由上述经典调和分析可知,当加载青岛港口观测站1年多的潮汐水位数据时,得到的各分潮振幅和迟角的等数值为常数(如表1所示)。S_TIDE程序包反演各分潮参数时,使用不同的独立点个数会得到不同变化趋势的值,下面演示在青岛港观测站,独立点个数1、2、3和5时S_TIDE反演的M2和S2分潮的振幅变化。
由图3知,当独立点个数为1时,得到的M2和S2分潮振幅分别为137.823 cm、42.4772 cm,与经典调和分析的结果一致。当独立点个数为2时,M2和S2分潮的振幅呈现线性变化趋势。M2分潮的振幅随着时间递增逐渐减小,S2分潮的振幅随着时间的递增逐渐增加,两端差值均约为2 cm。当独立点个数为3时,M2分潮振幅的变化趋势呈现“标准型”的特征,随时间的递增先增大后减小,在4432h处达到最大值约为140.1 cm。S2分潮的振幅变化与M2分潮变化趋势相反,随时间的递增先减小后增大,在4682 h处达到最小值约为38.6 cm。当独立点个数为4时,M2和S2分潮的振幅的变化趋势类似于独立点个数为3时。因此,随着独立点个数的不断增加,非线性趋势越来越明显,峰值和谷值点的个数递增。
4.2.2. 平均海平面的变化
本节在青岛港观测站,进行一系列的灵敏度实验,其中平均海平面的IP数从1增加到5。不同独立点下S_TIDE反演的平均海平面变化,如图4所示。
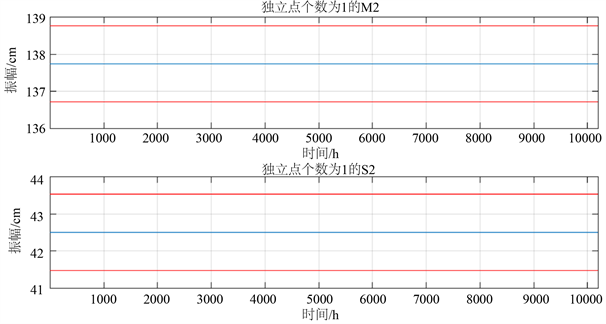
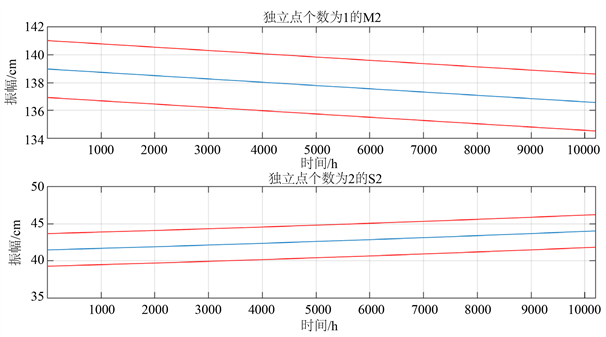

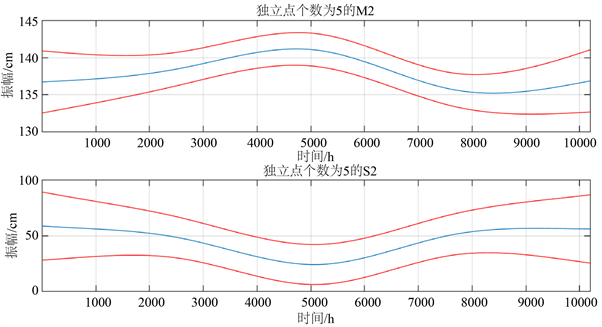
Figure 3. Amplitude change of S_TIDE inversion M2 and S2 moisture at different independent points (red solid line is 95% confidence interval)
图3. 不同独立点下S_TIDE反演的M2和S2分潮的振幅变化(红色实线为95%置信区间)

Figure 4. Mean sea level change of S_TIDE inversion at different independent points
图4. 不同独立点下S_TIDE反演的平均海平面变化
由图4知,随着IP数的增加,S_TIDE获得的平均海平面显示出更多的振荡。事实上,不同IP数的S_TIDE得到的平均海平面表示平均海平面不同时间尺度上的振荡。故S_TIDE可以发挥低通滤波器的作用,而截止频率取决于IP数。当独立点个数为1、2和3时,得到的平均海平面具有高度一致的变化趋势。然而,当独立点个数为5时获得的平均海平面似乎与之前获得的平均海平面略有不同,出现一个峰值和一个谷值。
4.3. S_TIDE的实用性
为了进一步验证S_TIDE程序包改进的优良性,选择日本的钏路(Kushiro)验潮站进行潮汐水位分析,钏路(Kushiro)验潮站位于北海道东南钏路川口,港市之东南,临太平洋,有南北防波堤港,船舶由两防波堤间入港,限制吃水9.3米;港内自南而北主要有:南突提北侧两个泊位,总长309米,水深5.4~7.5米。港区在严冬季节1~3月有冻结,但碍航仅10天左右;夏季多雾。收集钏路(Kushiro)验潮站1993年1月1日至2012年12月31日的潮位数据,其仿真试验的数据可从网站https://www.psmsl.org/下载。
按照上述步骤,采用S_TIDE程序包分析钏路(Kushiro)验潮站潮汐水位数据,结果如图5所示。
由图5知,为更清晰地比较回报水位,截取当独立点个数为1时,前300 h的回报水位数据,T_TIDE和S_TIDE程序包计算得到的回报潮汐水位变化趋势一致,故此时S_TIDE计算结果与T_TIDE相同。当独立点个数为21时,S_TIDE反演的M2分潮的振幅呈现先增加后减小再增加的趋势,出现一个峰值和
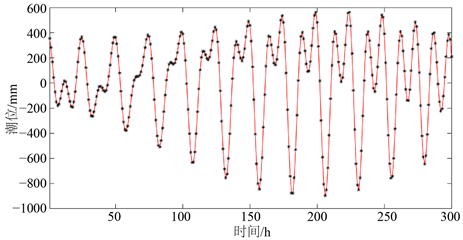

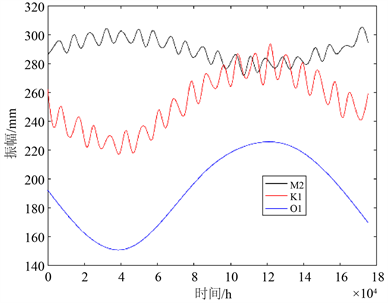
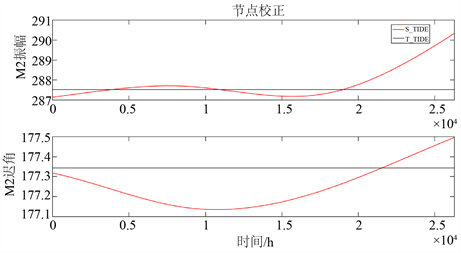
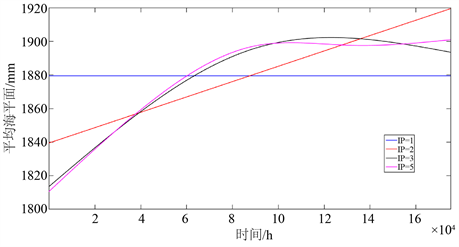
Figure 5. The analysis results of tide measuring station in Kushiro
图5. 钏路验潮站的分析结果
一个谷值。S_TIDE反演的S2分潮的振幅在135 mm附近浮动,浮动数值不超过5 mm。使用s_tide.m计算得到M2、K1和O1的振幅变化,其中M2和K1使用了50个独立点,反演得到的振幅变化包含了高频波动,而O1只使用了5个独立点,反演得到的振幅变化只有低频波动。在Kushiro站,S_TIDE反演的M2分潮振幅一开始在T_TIDE反演的M2分潮振幅附近浮动,在20000 h之后,逐渐远离T_TIDE反演的结果,反演迟角变化几乎一致。在不同独立点下,使用S_TIDE反演的平均海平面,当独立点个数为1和2时,均呈线性化趋势,当独立点个数为3时,平均海平面变化趋势呈现“偏峰型”特征,且与使用5个独立点得到的曲线变化趋势几乎相同。
5. 结论
基于IP格式和三次样条插值,提出了一种新的处理非平稳潮汐的增强调和分析方法。该方法从广泛使用的T_TIDE程序包中开发出来,通过MATLAB工具箱S_TIDE实现。
在本研究中,S_TIDE被应用于青岛港口观测站1年多的潮汐水位数据。将该方法与T_TIDE进行了比较,以显示其效率。进行灵敏度实验,详细讨论了IP数的选择。当独立点个数为1时,T_TIDE和S_TIDE程序包计算得到的回报潮汐水位相同。使用S_TIDE程序包求解各分潮随时间变化的振幅和迟角以及变化的平均海平面,结果发现,当独立点个数为1时,得到的M2和S2分潮振幅与经典调和分析的结果一致。随着独立点个数的不断增加,非线性趋势越来越明显,峰值和谷值点的个数递增。随着IP数的增加,S_TIDE获得的平均海平面显示出更多的振荡。此外,为了验证S_TIDE程序包的实用性,选择日本的钏路(Kushiro)验潮站进行潮汐水位分析。
综上所述,虽然S_TIDE不能用于预测,但有潜力用于未来河口和沿海海域非线性、时变动力学的研究。
基金项目
山东省自然科学基金(ZR2019PA007)。
文章引用
刘 倩,孙小淇. 改进的T_TIDE程序包在潮汐中的应用
Application of Improved T_TIDE Package in Tide[J]. 应用数学进展, 2021, 10(01): 160-171. https://doi.org/10.12677/AAM.2021.101019
参考文献
- 1. 邱志雄. 航海概论[M]. 北京: 人民交通出版社, 1999: 86-95.
- 2. Hoitink, A.J.F. and Jay, D.A. (2016) Tidal River Dynamics: Implications for Deltas. Reviews of Geophysics, 54, 240-272. https://doi.org/10.1002/2015RG000507
- 3. Jay, D.A. and Flinchem, E.P. (1999) A Comparison of Methods for Analysis of Tidal Records Containing Multi-Scale Non-Tidal Background Energy. Continental Shelf Research, 19, 1695-1732. https://doi.org/10.1016/S0278-4343(99)00036-9
- 4. Jay, D.A. and Kukulka, T. (2003) Revising the Paradigm of Tidal Analysis—The Uses of Non-Stationary Data. Ocean Dynamics, 53, 110-125. https://doi.org/10.1007/s10236-003-0042-y
- 5. Matte, P., Jay, D.A. and Zaron, E.D. (2013) Adaptation of Classical Tidal Harmonic Analysis to Nonstationary Tides, with Application to River Tides. Journal of Atmospheric and Oceanic Technology, 30, 569-589. https://doi.org/10.1175/JTECH-D-12-00016.1
- 6. Matte, P., Secretan, Y. and Morin, J. (2014) Temporal and Spatial Variability of Tidal-Fluvial Dynamics in the St. Lawrence Fluvial Estuary: An Application of Nonstationary Tidal Harmonic Analysis. Journal of Geophysical Research: Oceans, 119, 5724-5744. https://doi.org/10.1002/2014JC009791
- 7. Kukulka, T. and Jay, D.A. (2003) Impacts of Columbia River Discharge on Salmonid Habitat: 1. A Nonstationary fluvial Tide Model. Journal of Geophysical Research, 108, 3293. https://doi.org/10.1029/2002JC001382
- 8. Kukulka, T. and Jay, D.A. (2003) Impacts of Columbia River discharge on Salmonid Habitat: 2. Changes in Shallow-Water Habitat. Journal of Geophysical Research, 108, 3294. https://doi.org/10.1029/2003JC001829
- 9. Pawlowicz, R., Beardsley, B. and Lentz, S. (2002) Classical Tidal Harmonic Analysis Including Error Estimates in MATLAB Using T_TIDE. Computational Geosciences, 28, 929-937. https://doi.org/10.1016/S0098-3004(02)00013-4
- 10. Huber, P.J. (1996) CBMS-NSF Regional Conference Series in Applied Mathematics: Robust Statistical Procedures. 2nd Edition, Vol. 68, Society of Industrial and Applied Mathematics, Philadelphia, 67. https://doi.org/10.1137/1.9781611970036
- 11. Leffler, K.E. and Jay, D.A. (2009) Enhancing Tidal Harmonic Analysis: Robust (Hybrid L1/L2) Solutions. Continental Shelf Research, 29, 78-88. https://doi.org/10.1016/j.csr.2008.04.011
- 12. Jin, G.Z., Pan, H.D., Zhang, Q.L., Lv, X.Q., Zhao, W. and Gao, Y. (2018) Determination of Harmonic Parameters with Temporal Variations: An Enhanced Harmonic Analysis Algorithm and Application to Internal Tidal Currents in the South China Sea. Journal of Atmospheric and Oceanic Technology, 35, 1375-1398. https://doi.org/10.1175/JTECH-D-16-0239.1
- 13. Pan, H.D., Lv, X.Q., Wang, Y.Y., Matte, P. and Jin, G.Z. (2018) Exploration of Tidal-Fluvial Interaction in the Columbia River Estuary Using S_TIDE. Journal of Geophysical Research: Oceans, 123, 6598-6619. https://doi.org/10.1029/2018JC014146
- 14. Foreman, M.G.G. and Henry, R.F. (1989) The Harmonic Analysis of Tidal Model Time Series. Advances in Water Resources, 12, 109-120. https://doi.org/10.1016/0309-1708(89)90017-1
- 15. Godin, G. (1972) The Analysis of Tides. University of Toronto Press, Toronto, 264.
- 16. Guo, Z., Pan, H.D., Fan, W. and Lv, X.Q. (2017) Application of Surface Spline Interpolation in Inversion of Bottom Friction Coefficients. Journal of Atmospheric and Oceanic Technology, 34, 2021-2028. https://doi.org/10.1175/JTECH-D-17-0012.1
- 17. Lu, X.Q. and Zhang, J.C. (2006) Numerical Study on Spatially Varying Bottom Friction Coefficient of a 2D Tidal Model with Adjoint Method. Continental Shelf Research, 26, 1905-1923. https://doi.org/10.1016/j.csr.2006.06.007
- 18. Pan, H.D., Guo, Z. and Lv, X.Q. (2017) Inversion of Tidal Open Boundary Conditions of the M2 Constituent in the Bohai and Yellow Seas. Journal of Atmospheric and Oceanic Technology, 34, 1661-1672. https://doi.org/10.1175/JTECH-D-16-0238.1
- 19. Zhang, J., Lu, X., Wang, P. and Wang, Y.P. (2011) Study on Linear and Nonlinear Bottom Friction Parameterizations for Regional Tidal Models Using Data Assimilation. Continental Shelf Research, 31, 555-573. https://doi.org/10.1016/j.csr.2010.12.011
- 20. Guo, Z., Pan, H.D., Cao, A.Z. and Lv, X.Q. (2018) A Harmonic Analysis Method Adapted to Capturing Slow Variations of Tidal Amplitudes and Phases. Continental Shelf Research, 164, 37-44. https://doi.org/10.1016/j.csr.2018.06.005
- 21. Huang, N.E., Shen, Z., Long, S.R., Wu, M. C., Shih, H.H., Yen, N., et al. (1998) The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Royal Society Publication, 454, 903-995. https://doi.org/10.1098/rspa.1998.0193
- 22. Malik, R., Zhou, F. and Ceder, G. (2011) Kinetics of Non-Equilibrium Lithium Incorporation in LiFePO4. Nature Materials, 10, 587-590. https://doi.org/10.1038/nmat3065
