Advances in Applied Mathematics
Vol.
10
No.
10
(
2021
), Article ID:
45893
,
9
pages
10.12677/AAM.2021.1010355
过特征多边形始末端点的四次均匀B样条曲线及其应用
白根柱1,2
1浙江长征职业技术学院基础部,浙江 杭州
2内蒙古民族大学数理学院,内蒙古 通辽
收稿日期:2021年9月18日;录用日期:2021年10月11日;发布日期:2021年10月21日

摘要
本文构造了过控制多边形始点和终点的四次均匀B样条曲线,并以此四次均匀B样条曲线为轴线的管道光滑拼接了轴线异面管道。该方法相较于过始末端点的三次均匀B样条曲线为轴线的管道光滑拼接轴线异面管道,通过给定位于曲线上的一些点,反算出B样条曲线的特征多边形的顶点构造的B样条曲线为轴线的管道光滑拼接轴线异面的管道有其不同的特性。具有一定的应用价值。
关键词
B样条,光滑拼接,轴线异面,拼接管道

Quadratic Uniform B-Spline Curve of Passing Start Point and End Point of the Characteristic Polygon and Its Application
Genzhu Bai1,2
1Basis Department, Zhejiang Changzheng Vocational & Technical College, Hangzhou Zhejiang
2College of Mathematics and Physics, Inner Mongolia University for the Nationalities, Tongliao Inner Mongolia
Received: Sep. 18th, 2021; accepted: Oct. 11th, 2021; published: Oct. 21st, 2021

ABSTRACT
In this paper, we construct a quartic uniform B-spline curve of passing start point and end point of the control polygon. Tubes whose axes are in non-coplaner are smoothly blended by tube taking a quartic uniform B-spline curve as its axis. Compared with the tube with cubic uniform B-spline curve as the axis passing through the start and end points, the tubes whose axes are in non-cop- laner are smoothly blended by the tube. By giving some points located on the curve, this method can calculate the vertices of the characteristic polygon of the B-spline curve. The constructed B- spline curve is used as the tube with axis, and tubes are smoothly blended by the tube whose axis is in non-coplaner which has different characteristics. It has certain application value.
Keywords:B-Spline, Smooth Blending, Non-Coplaner, Blending Tube

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
我们在文 [1] 中,根据实际问题给定B样条曲线的控制多边形的顶点,构造轴线异面管道的拼接管道。在文 [2] [3] [4] 中,假定B样条曲线过某些固定的点,反过来求B样条曲线的实际控制顶点,构造轴线异面管道的拼接曲面。两种方法具有明显的优缺点:前者,拼接管道由多段光滑拼接的管道构成,光顺性较好,应用广泛,不仅能应用于轴线异面圆管道的拼接,还能应用于椭圆管道的拼接,实际应用时加工复杂。后者,拼接管道的构造可根据需要尽量简单,由一段或两段光滑拼接的管道构成,加工容易。但是,应用范围受限,不能应用于轴线异面椭圆管道的拼接。
本文研究四次均匀B样条曲线过控制多边形始末端点的条件,并讨论光滑拼接轴线异面管道拼接问题。
设
和
是两个待拼接的管道表达式,其中a是管道的半径,
分别是
和
时的法矢和副法矢。管道轴线的表达式为
和
2. 过始末端点的四次均匀B样条曲线
定义1设
是四次均匀B样条曲线段。其中
为B样条基,
为特征多边形的顶点。
为了使所求B样条曲线过特征多边形的始点
和终点
,我们在
的反向延长线上取
,在
的延长线上取
。在(1)中,可令
,得
并令
,解得
(2)
同理,令
,得
并令
,解得
(3)
式(2)和(3)即为四次均匀B样条曲线过控制多边形的始末端点的条件。
先构造过始末端点的光滑拼接轴线的四次均匀B样条曲线。
例1设
,分别取
和
。带入公式(2)和(3),分别得
,,,,,。用以上三组点序列为顶点
的四次均匀B样条曲线拼接轴线异面管道的表达式为
(4)
(5)
(6)
是三条三段连续的四次B样条曲线。
分别与异面轴线拼接效果如图1:
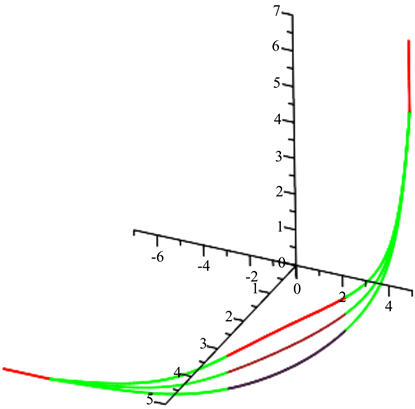
Figure 1. When V2 takes
and
respectively, the effect diagram
图1. V2分别取
和
时,与异面轴线拼接效果图
由例1可以看出:
1) 用过始末端点的四次均匀B样条曲线光滑拼接异面轴线,与 [1] 一样也需要三段曲线;
2) 曲线位置与
的位置相关,
在上,拼接曲线位于上侧;
居中,拼接曲线在中间;
在下边,拼接曲线在下侧;
3) 从拼接效果看,轴线拼接效果没有太大差异,光滑度很好。
3. 过始末端点的四次均匀B样条曲线及其在轴线异面管道拼接中的应用
基于轴线光滑拼接的异面管道拼接方法,在 [5] [6] [7] [8] [9] 中进行了详细讨论。下面考察过控制多边形始末端点的四次均匀B样条曲线在管道拼接中的效果。
例2设
和
构造以轴线
为轴线的圆管道
:
其中,
是三段光滑拼接的圆管道,
和
是构造的B样条曲线的主法矢和副法矢。其拼接效果如图2:
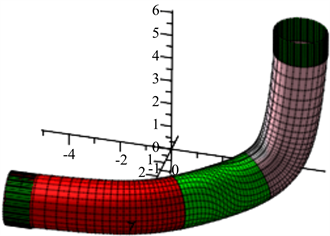
Figure 2. When
, circular pipe stitching effect drawing
图2.
时,圆管道拼接效果图
例3设
和
构造以轴线
为轴线的椭圆管道
:
其中,
是三段光滑拼接的管道,
和
是构造的B样条曲线的主法矢和副法矢,
由(5)式给出。
其拼接效果如图3:
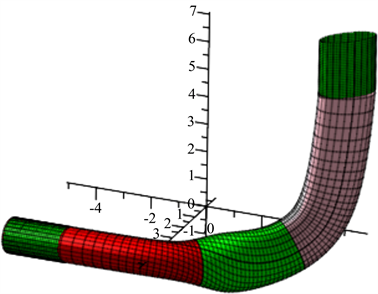
Figure 3. When
, the effect picture of elliptical pipeline splicing
图3.
时,椭圆管道拼接效果图
例4设
和
构造以轴线
为轴线的椭圆管道
:
其中,
是三段光滑拼接的管道,
和
是构造的B样条曲线的主法矢和副法矢,
由(6)式给出。
其拼接效果如图4:

Figure 4. When
, the effect picture of elliptical pipeline splicing
图4.
时,椭圆管道拼接效果图
由例2、例3和例4可以看出,在
取定的情况下,用我们所构造的管道拼接轴线异面管道,还需要优化以下几点:
1) 拼接效果与
的选取有关,对于椭圆管道拼接需要优化
的选取方法;
2) 用三段连续的四次均匀B样条曲线为轴线的管道拼接轴线异面椭圆管道,段与段之间能够光滑拼接。要想取得视觉上的光顺效果,还需要用 [8] 中给出的方法,逐步旋转椭圆管道的长半轴与短半轴来实现;
3) 用三段连续的四次均匀B样条曲线为轴线的管道拼接轴线异面椭圆管道,对于异面椭圆管道的长半轴和短半轴的方向有特殊要求,也需要逐步旋转每段拼接椭圆管道的长半轴与短半轴来实现。
4. 结束语
过始末端点的四次B样条曲线为轴线的管道拼接轴异面管道需要三段管道,光顺性取决于控制顶点
的选取。对于椭圆管道拼接更为明显。需要优化
点的选取。尽管相较于插值于两端点的三次有理B样条曲线、插值于制定点的三次B样条曲线和四次B样条曲线段数多,但是段与段之间的光顺程度较好,且能够应用于椭圆管道的拼接。所以,比以上三种情形具有更好的应用前景。
基金项目
国家自然科学基金项目资助(11561052)。
文章引用
白根柱. 过特征多边形始末端点的四次均匀B样条曲线及其应用
Quadratic Uniform B-Spline Curve of Passing Start Point and End Point of the Characteristic Polygon and Its Application[J]. 应用数学进展, 2021, 10(10): 3381-3389. https://doi.org/10.12677/AAM.2021.1010355
参考文献
- 1. 白根柱. 基于轴线光滑拼接的轴线异面管道拼接技术[J]. 应用数学进展, 2019, 8(7): 1267-1271.
https://doi.org/10.12677/AAM.2019.87147
- 2. 白根柱. 过指定顶点的三次B样条曲线及其应用[J]. 应用数学进展, 2020, 9(10): 1821-1828.
https://doi.org/10.12677/AAM.2020.910211
- 3. 白根柱. 三次有理B样条曲线及其应用[J]. 应用数学进展, 2020, 9(8): 1331-1337.
https://doi.org/10.12677/AAM.2020.98157
- 4. 白根柱. 过指定顶点的四次B样条曲线及其应用[J]. 应用数学进展, 2021, 10(8): 2739-2747.
https://doi.org/10.12677/AAM.2021.108285
- 5. Bai, G.Z., Liu, S.Y., Wang, H., Wu, Z. and Yin, Z.J. (2014) A Novel Method for Smooth Blending Cylindrical Surfaces Whose Axes Are Non-Coplanar with Intersecting Line of Two Tapered Surfaces. Applied Mechanics and Materials, 687-691, 1470-1473. https://doi.org/10.4028/www.scientific.net/AMM.687-691.1470
- 6. Bai, G.Z. and Wu, Z. (2019) Intersection Line of Conical Surfaces and Its Application in the Blending of Tubes with Non-Coplanar Axes. International Journal of Applied Physics and Mathematics, 9, 152-157.
https://doi.org/10.17706/ijapm.2019.9.4.152-157
- 7. Bai, G.Z., Wu, Z. and Lin, X. (2017) Intersection Line of Conical Surface and Smoothly Blending of Two Tubes Whose Axes are Non-Coplanar. Journal Applied Mathematics and Physics, 5, 1887-1991.
https://doi.org/10.4236/jamp.2017.59158
- 8. Bai, G.Z. and Wu, Z. (2019) Intersection Line of Conical Surfaces and Its Application in the Blending of Tubes with Non-Coplanar Axes. International Journal of Applied Physics and Mathematics, 9, 152-157.
https://doi.org/10.17706/ijapm.2019.9.4.152-157
- 9. 乌仁高娃, 陶吐格, 白根柱. Hartmann函数在椭圆管道拼接中的应用[J]. 应用数学进展, 2019, 8(11): 1700-1707.
https://doi.org/10.12677/AAM.2019.811199









