Pure Mathematics
Vol.05 No.05(2015), Article ID:15987,5 pages
10.12677/PM.2015.55026
Probability Problem in Trajectory Simulation of Target Movement
Yuhong Jin, Xinpeng Wang*
College of Science, Naval University of Engineering, Wuhan Hubei
Email: jin_yuhong@sina.cn, *1204297054@qq.com
Received: Aug. 12th, 2015; accepted: Sep. 1st, 2015; published: Sep. 4th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
This paper studies the equivalence of the probability distributions of two different ways by which the position error in trajectory simulation of target moving is represented. The results show that the two ways are equivalent only under special given conditions, but usually not under general conditions.
Keywords:Moving Target, Trajectory Simulation, Error, Probability Distributions, Equivalence
目标运动轨迹仿真中的概率问题
金裕红,王新鹏*
海军工程大学理学院,湖北 武汉
Email: jin_yuhong@sina.cn, *1204297054@qq.com
收稿日期:2015年8月12日;录用日期:2015年9月1日;发布日期:2015年9月4日

摘 要
本文研究目标运动轨迹仿真中误差表示的两种不同方式的概率等价性问题,研究结果表明,只有在非常特殊的条件下,关于误差概率分布的假设才是等价的,一般情况下则不具有等价性。
关键词 :运动目标,轨迹仿真,误差,概率分布,等价性

1. 引言与预备知识
考虑点目标做空间运动,目标运动的初始位置为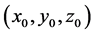 ,速度为
,速度为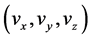 ,则在时刻
,则在时刻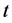 的理想位置应为:
的理想位置应为:
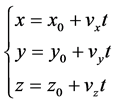 (1)
(1)
由于运动环境与目标自身控制因素等的影响,目标的实际位置与理想位置会有适度的偏差。在仿真处理过程中,对目标的真实轨迹有多种设计方法[1] 。若目标总体的运动趋势为匀速直线运动,则常采用如下两种方式处理。
方式1:
设真实位置为如下随机变量形式:
 (2)
(2)
其中随机误差变量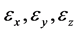 服从均值为0,方差分别为
服从均值为0,方差分别为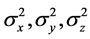 的正态分布,且三者相互独立。目标沿三个坐标方向的速度分量假定为确定的数值,尽管这一假定的合理性并不充分,但可以认为在目标做近似匀速运动的前提下,将速度的随机成分归于真实位置描述中的随机误差,这也是仿真目标运动轨迹时的一种通用处理方法[2]
。
的正态分布,且三者相互独立。目标沿三个坐标方向的速度分量假定为确定的数值,尽管这一假定的合理性并不充分,但可以认为在目标做近似匀速运动的前提下,将速度的随机成分归于真实位置描述中的随机误差,这也是仿真目标运动轨迹时的一种通用处理方法[2]
。
方式2:
设真实位置为如下随机变量形式:
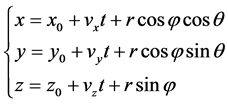 (3)
(3)
其中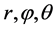 为相互独立的随机变量;
为相互独立的随机变量;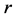 在
在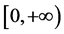 上取值,服从Maxwell分布;
上取值,服从Maxwell分布; 在
在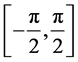 上取值,其概率密度函数在该区间上为
上取值,其概率密度函数在该区间上为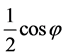 ;
;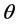 服从区间
服从区间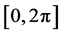 上的均匀分布。
上的均匀分布。
上述两种处理方式从形式上来看似乎是一致的,只不过方式2更适合于描述目标位置或误差向量,在工程上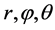 分别表示误差向量
分别表示误差向量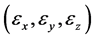 的距离(长度)、俯仰角与方位角。
的距离(长度)、俯仰角与方位角。
本文研究这两种方式的概率假设的一致性问题,即随机变量 与
与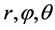 的概率分布假设是否一致:一是
的概率分布假设是否一致:一是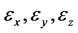 相互独立是否等价于
相互独立是否等价于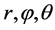 相互独立;二是
相互独立;二是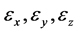 的联合分布与
的联合分布与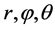 的联合分布能否互推。
的联合分布能否互推。
2. 两种仿真模型的概率分布及等价性问题
在问题的研究过程中,下述命题是必须的:
命题1 [3] :若 维连续型随机向量
维连续型随机向量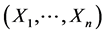 的联合密度函数为
的联合密度函数为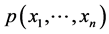 。已知存在
。已知存在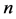 个Borel可测函数:
个Borel可测函数:
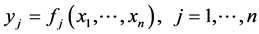 ,
,
使得
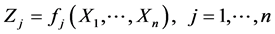 ,
,
并且对于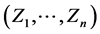 的每一组可能值
的每一组可能值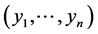 ,方程组
,方程组


都有唯一解
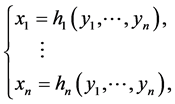
其中每个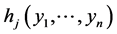 都有一阶连续偏导数,则随机向量
都有一阶连续偏导数,则随机向量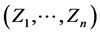 是连续型的,其联合密度函数
是连续型的,其联合密度函数
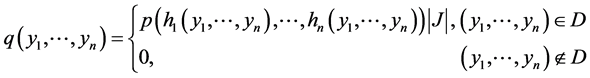
其中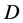 是随机向量
是随机向量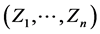 的所有可能值的集合,
的所有可能值的集合,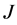 是变换的Jacobi行列式,
是变换的Jacobi行列式,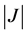 是
是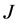 的绝对值。
的绝对值。
根据该命题,若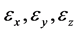 是均值为0,方差分别为
是均值为0,方差分别为 的相互独立的服从正态分布的随机变量,则三者的联合分布为三维正态分布。记
的相互独立的服从正态分布的随机变量,则三者的联合分布为三维正态分布。记 ,则
,则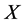 服从分布
服从分布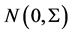 ,其中0为三维零向量,
,其中0为三维零向量,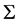 为三阶对角阵
为三阶对角阵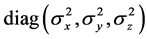 。
。
易知变换
 (4)
(4)
是变量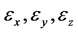 与变量
与变量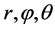 之间的一一变换(原点除外),对应的Jacobi行列式为:
之间的一一变换(原点除外),对应的Jacobi行列式为:
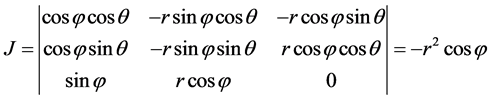 ,
,
即: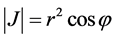 ,
,
从而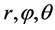 的联合概率密度函数
的联合概率密度函数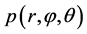 为:
为:
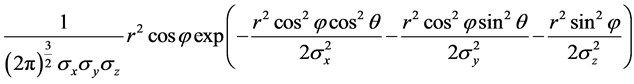 ,
,
由此可见,即使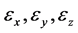 相互独立,一般来说,由式(4)得到的随机变量
相互独立,一般来说,由式(4)得到的随机变量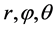 并非相互独立,这也反映了运动轨迹方式1与方式2的本质差异。
并非相互独立,这也反映了运动轨迹方式1与方式2的本质差异。
这里有一种特殊情形,若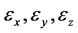 的方差存在均相等,即
的方差存在均相等,即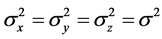 时,有:
时,有:
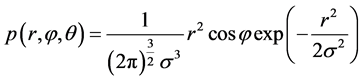 (5)
(5)
从式(5)不难看出,随机变量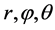 相互独立,且随机变量
相互独立,且随机变量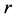 服从Maxwell分布,即其概率密度函数:
服从Maxwell分布,即其概率密度函数:
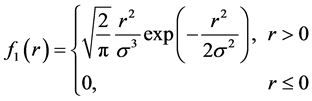 (6)
(6)
随机变量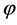 的概率密度函数为:
的概率密度函数为:
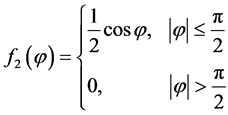 (7)
(7)
随机变量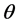 服从区间
服从区间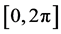 上的均匀分布,即其概率密度函数为:
上的均匀分布,即其概率密度函数为:
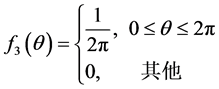 (8)
(8)
反过来,若随机变量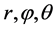 相互独立,且相应的概率密度函数分别为式(6),(7),(8),则根据命题1,可计算
相互独立,且相应的概率密度函数分别为式(6),(7),(8),则根据命题1,可计算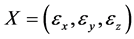 的联合概率密度函数
的联合概率密度函数 ,其中
,其中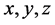 分别表示随机变量
分别表示随机变量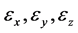 的取值,与式(1),(2),(3)中的
的取值,与式(1),(2),(3)中的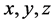 不同。对应的Jacobi行列式为:
不同。对应的Jacobi行列式为:

从而得到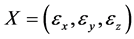 的联合概率密度函数:
的联合概率密度函数:
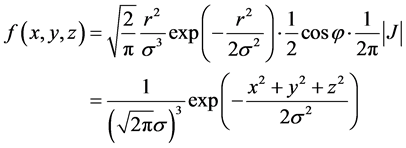 (9)
(9)
该表达式说明此时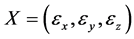 的联合分布为三维正态分布,且均值都为零,方差
的联合分布为三维正态分布,且均值都为零,方差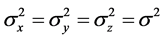 。
。
3. 结论
研究结果表明,若仅仅假设随机变量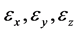 相互独立且联合分布为三维正态分布,则相应的
相互独立且联合分布为三维正态分布,则相应的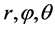 并非相互独立;若假定
并非相互独立;若假定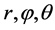 相互独立,且相应的分布如(6),(7),(8)所示,则该假设等价于
相互独立,且相应的分布如(6),(7),(8)所示,则该假设等价于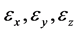 相互独立,且均为均值为零,方差相等的正态随机变量。
相互独立,且均为均值为零,方差相等的正态随机变量。
文章引用
金裕红,王新鹏. 目标运动轨迹仿真中的概率问题
Probability Problem in Trajectory Simulation of Target Movement[J]. 理论数学, 2015,
05(05): 171-175. http://dx.doi.org/10.12677/PM.2015.55026
参考文献 (References)